Answers
Answer:
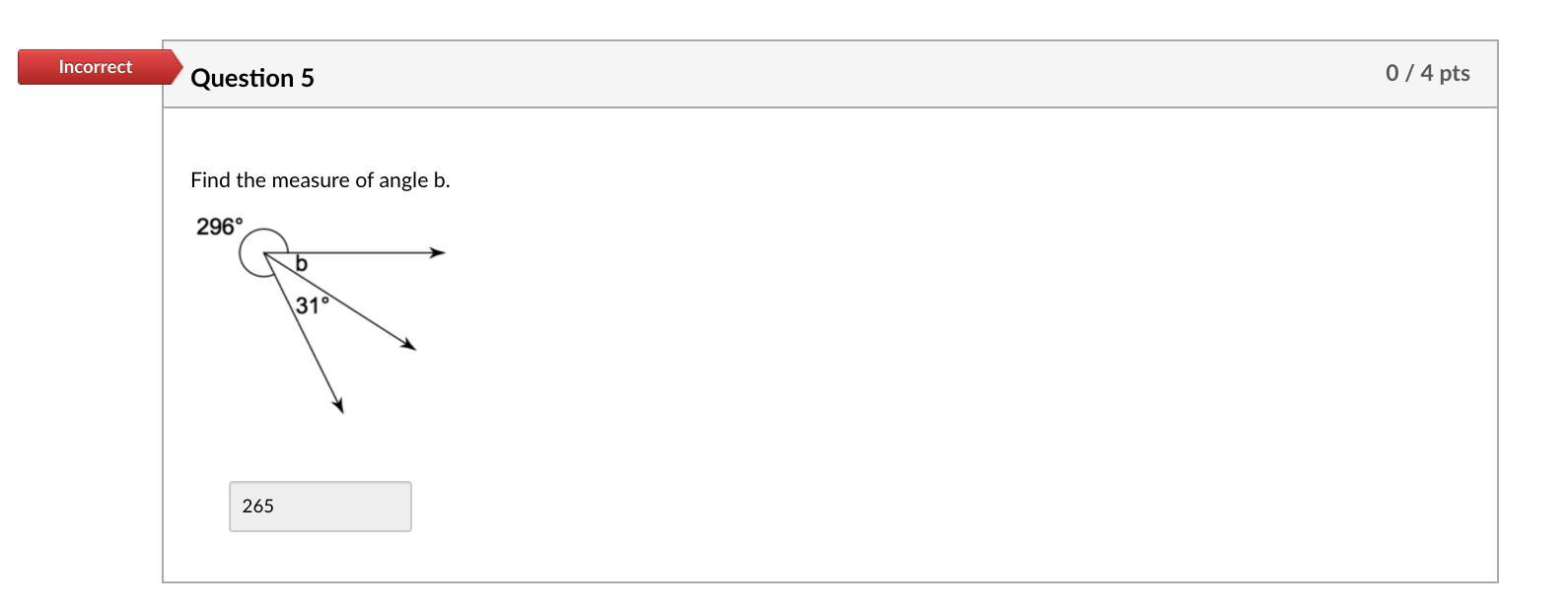
b = 33°
Step-by-step explanation:
A full circle is 360°.
360° - 296° - 31° = b
360° - 296° - 31° = 33°
Answer:
b = 33°
Step-by-step explanation:
b + 31° + 296° = 360°
b + 327°= 360°
b = 360° - 327°
b = 33°
Related Questions
HELP PLEASE QUICKLY!!!!!!!!

Answers
The measure of angle A is 63°, the measure of side b is 22.34 feet and the measure of side a is 37.57 feet.
From the given triangle ABC,
∠A+∠B+∠C=180° (Angle sum property of a triangle)
∠A+32°+85°=180°
∠A+117°=180°
∠A=180°-117°
∠A=63°
We know that, the formula for sine rule is sinA/a=sinB/b=sinC/c
Here, sin63°/a = sin32°/b = sin85°/42
sin63°/a = sin32°/b = 0.9961/42
sin32°/b = 0.9961/42 and sin63°/a = 0.9961/42
0.5299/b = 0.9961/42
0.9961b=22.2558
b=22.2558/0.9961
b=22.34 feet
sin63°/a = 0.9961/42
0.8910/a = 0.9961/42
0.9961a=37.422
a=37.422/0.9961
a=37.57 feet
Therefore, the measure of angle A is 63°, the measure of side b is 22.34 feet and the measure of side a is 37.57 feet.
Learn more about the sine rule here:
https://brainly.com/question/22288720.
#SPJ1
researcher is using a Kruskal-Wallis test to evaluate the difference between three treatment conditions using a sample of n-8 in each treatment. What value of H is necessary to conclude that there is a significant difference among the treatments using a 05 Select one O a. H25.99 Ob. H2 347 c H2 1.96 O d. H 2080
Answers
C. H2 1,96
To establish whether there is a significant difference between treatments using the Kruskal-Wallis test, the calculated value of H should be compared to the critical values in the table of H values. The critical value of H to use depends on the significance level chosen for the test (0.05 in this case).
Using a significance level of 0.05, the critical value of H for a sample size of n-8 for each treatment is approximately H2 1.96. That is, if the calculated H value is greater than 1.96, we can conclude that there is a significant difference between the treatments.
Hence, the correct answer in this case is c. H2 1,96
Read more about Kruskal-Wallis test on brainly.com/question/29106748
#SPJ4
Lightfoot Inc., a software development firm, has stock outstanding as follows: 20,000 shares of cumulative preferred 2% stock, $20 par, and 25,000 shares of $100 par common. During its first four years of operations, the following amounts were distributed as dividends: first year, $3,000; second year, $5,000; third year, $34,500; fourth year, $71,000.
Answers
The amount of Dividends of $3,000, $5,000, $34,500, and $71,000 were distributed to the 20,000 preferred and 25,000 common shareholders of Lightfoot Inc. over the first four years of operations.
To calculate the dividend per share of the preferred and common stock of Lightfoot Inc., the total amount of dividends paid out over the first four years must first be determined. This can be done by adding the given amounts of $3,000, $5,000, $34,500, and $71,000 to get a total of $113,500. To find the dividend per share for the preferred stock, the total dividend is divided by the number of shares (20,000) which gives a dividend per share of $5.68. To find the dividend per share for the common stock, the total dividend is divided by the number of shares (25,000) which gives a dividend per share of $4.54.
Learn more about amount here
https://brainly.com/question/8082054
#SPJ1
Solve for X
5(3X-2)=5
Answers
please help! math question!

Answers
Simplifying, the exponents expression, we have 63y/xu⁴
What are exponents?Exponents are the powers to which a particular number is raised.
How to simplify the expression?Given the expression 3y⁻⁴ . 3y⁵x⁸u⁻⁵.7x⁻⁹. To simplify the expression, we use the product rule of exponents which states that for a given base x, xᵃ xᵇ = xᵃ⁺ᵇ.
So, applying this rule to the expression and collecting common bases, we have that
3y⁻⁴ . 3y⁵x⁸u⁻⁵u.7x⁻⁹ = 3y⁻⁴ × 3y⁵ × x⁸ × 7x⁻⁹ × u⁻⁵ × u
= 3 × 3 × y⁻⁴ × y⁵ × 7 × x⁸ × x⁻⁹ × u⁻⁵ × u
Applying the product rule, we have that
= 3 × 3 × y⁻⁴ ⁺ ⁵ × 7 × x⁸ ⁺(⁻⁹) × u⁻⁵ ⁺ ¹
= 3 × 3 × y⁻⁴ ⁺ ⁵ × 7 × x⁸ ⁻ ⁹ × u⁻⁵ ⁺ ¹
= 3 × 3 × y × 7 × x⁻¹ × u⁻⁴
= 3 × 3 × 7 × y × x⁻¹ × u⁻⁴
Using the reciprocal rule that x⁻ⁿ = 1/xⁿ, we have that
= 3 × 3 × 7 × y × x⁻¹ × u⁻⁴
= 63 × y × 1/x × 1/u⁴
= 63y/xu⁴
So, simplifying, we have 63y/xu⁴
Learn more about exponents here:
https://brainly.com/question/29863607
#SPJ1
Susan made $550 baby sitting during the summer. She made $256 helping her grandmother working on the farm She spent $175 on a new dress. Which number sentence could be used to find how much money Susan had left?
1. $550 - $256 + $75
2. $550 - $256 - $75
3. $550 + $256 + $75
4. $550 + $256 + $75
Answers
Please help! Only answer if correct :)!!

Answers
Answer:
x....y
0....-9
-9...0
Solution:
Draw a line thru the 2 points.
Do the same for the other eqn. Where they incersect is the solution.
Here's the solution in attachment


A commuter plane provides transportation from an international airport to surrounding cities. One commuter plane averaged 260 mph flying to a city and 140 mph returning to the international airport. The total flying time was 4 h. Find the distance between the two airports.
Answers
Answer:
364 miles
Step-by-step explanation:
Rate Time Distance
Flight #1 260 x 260x
Flight #2 140 4-x 140(4-x)
Because each flight was to or from the same airports the distance traveled by flight #1 and flight #2 must be the same. This means that you can set the two calculated distances equal to each other.
260x = 140(4-x)
260x = 560 - 140x
400x = 560
x = 1.4 hours This is the amount of time flight 1 spent in the air.
now we can use this and plug it into the distance formula (260x) to find the distance
260(1.4) = 364
so the distance between the two airports is 364 miles
Hey, Can anyone assist me with a bunch of calculus questions, thank you in advance


Answers
Answer:
1. (a) [-1, ∞)
(b) (-∞, -1) ∪ (1, ∞)
2. (a) (1, 3)
(b) (-∞, 1) ∪ (3, ∞)
3. (a) 9.6 m and 0.4 m
(b) 03:08 and 15:42
Step-by-step explanation:
The domain of a function is the set of all possible input values (x-values).
The range of a function is the set of all possible output values (y-values).
Question 1Part (a)
When x < 0, the function is f(x) = x².
Since the square of any non-zero real number is always positive, the range of the function f(x) for x < 0 is (0, ∞).
When x ≥ 0, the function is f(x) = sin(x).
The minimum value of the sine function is -1 and the maximum value of the sine function is 1. As the sine function is periodic, the function oscillates between these values. Therefore, the range of function f(x) for x ≥ 0 is [-1, 1].
The range of function f(x) is the union of the ranges of the two separate parts of the function. Therefore, the range of f(x) is [-1, ∞).
Part (b)
The domain of the function g(x) = ln(x² - 1) is the set of all real numbers x for which (x² - 1) is positive, since the natural logarithm function (ln) is only defined for positive input values.
Find the values of x:
\(\implies x^2-1 > 0\)
\(\implies x^2 > 1\)
\(\implies x < -1, \;\;x > 1\)
Therefore, the domain of function g(x) is (-∞, -1) ∪ (1, ∞).
Question 2Part (a)
To determine the interval where f(x) < 0, we need to find the values of x for which the quadratic is less than zero.
First, set the function equal to zero and solve for x:
\(\begin{aligned} x^2-4x+3&=0\\x^2-3x-x+3&=0\\x(x-3)-1(x-3)&=0\\(x-1)(x-3)&=0\\ \implies x&=1,\;3\end{aligned}\)
Therefore, the function is equal to zero at x = 1 and x = 3 and so the parabola crosses the x-axis at x = 1 and x = 3.
As the leading coefficient of the quadratic is positive, the parabola opens upwards. Therefore, the values of x that make the function negative are between the zeros. So the interval where f(x) < 0 is 1 < x < 3 = (1, 3).
Part (b)
Since the square root of a negative number cannot be taken, and dividing a number by zero is undefined, function f(x) has to be positive and not equal to zero: f(x) > 0.
As the parabola opens upwards, the values of x that make the function positive are less than the zero at x = 1 and more than the zero at x = 3.
Therefore the domain of g(x) is (-∞, 1) ∪ (3, ∞).
Question 3Part (a)
The range of a sine function is [-1, 1]. Therefore, to calculate the maximal and minimal possible water depths of the bay, substitute the maximum and minimum values of sin(t/2) into the equation:
\(\textsf{Maximum}: \quad 5+4.6(1)=9.6\; \sf m\)
\(\textsf{Maximum}: \quad 5+4.6(-1)=0.4\; \sf m\)
Part (b)
To find the times when the depth is maximal, set sin(t/2) to 1 and solve for t:
\(\implies \sin \left(\dfrac{t}{2}\right)=1\)
\(\implies \dfrac{t}{2}=\dfrac{\pi}{2}+2\pi n\)
\(\implies t=\pi+4\pi n\)
Therefore, the values of t in the interval 0 ≤ t ≤ 24 are:
\(t = \pi=3.14159265...\sf hours\;after\;mindnight\)\(t=5 \pi = 15.7079632...\sf hours\;after\;mindnight\)Convert these values to times:
03:08 and 15:42HELP ASAP
What are the solutions to the following system of equations? 2x − y = 6 y = x2 − 9 (3, 0) and (−1, −8) (3, 0) and (4, 2) (−3, 0) and (−1, −8) (−3, 0) and (4, 2)
Answers
Answer:
I think so none
answer to the following steps below:-
I hope my answer helps.

Find the probability of getting 2 or 4 or 6 when a dice is rolled
Answers
Answer:
The probability of getting a 2, 4, or 6 when a dice is rolled is 1/2, or 50%. This is because there are six possible outcomes when a dice is rolled, and three of them are favorable outcomes (2, 4, or 6). Therefore, the probability of getting a 2, 4, or 6 is 3/6, which simplifies to 1/2 or 50%.
how many 1/2 cup servings are in 9 cups of cereal?
Answers
Answer:
18
Step-by-step explanation:
9 divided by 1/2 is the same as 9 multiplied by 2, which equals 18
Which statement best describes g(x) = ?X + 6 - 8 and the parent function f(x) = ?
The domains of g(x) and f(x) are the same, but their ranges are not the same.
O The ranges of g(x) and f(x) are the same, but their domains are not the same.
O The ranges of g(x) and f(x) are the same, and their domains are also the same.
O The domains of g(x) and f(x) are the not the same, and their ranges are also not the same.
Answers
Answer:
O The ranges of g(x) and f(x) are the same, but their domains are not the same.
Step-by-step explanation:
The statement that best describes g(x) and f(x) is:
The domains of g(x) and f(x) are the same, but their ranges are not the same.
Option A is the correct answer.
What is a function?A function has an input and an output.
A function can be one-to-one or onto one.
It simply indicated the relationships between the input and the output.
Example:
f(x) = 2x + 1
f(1) = 2 + 1 = 3
f(2) = 2 x 2 + 1 = 4 + 1 = 5
The outputs of the functions are 3 and 5
The inputs of the function are 1 and 2.
We have,
The function g(x) is obtained by taking the parent function f(x) = ∛x and performing a series of transformations:
- shifting the graph horizontally 6 units to the left
- shifting it vertically 8 units downward.
Since the cube root function is defined for all real numbers, both g(x) and f(x) have the same domain, which is the set of all real numbers.
However, the transformations applied to f(x) change the shape of the graph and the range of the function.
In particular,
g(x) is shifted 8 units downward, so its range is shifted down by 8 units compared to the range of f(x).
Therefore,
The domains of g(x) and f(x) are the same, but their ranges are not the same.
Learn more about functions here:
https://brainly.com/question/28533782
#SPJ7
PLEASE ANSWER ASAP FOR BRAINLEST!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

Answers
Given:
circumference of a circle = 11304 units.....
to find: diameter of the circle=2 x radius of the circle
2pi x r = 11304
=>r = 11304 x 7 /22 x 1/2
=>r = 1798 units...
hence,radius of the circle = 1798 units.....
therefore, diameter of the circle = 1798 x 2 = 3596 units......
Answer:
I think it is 3598.2 units

what is 15 ones dividend by eight and seven fifty eight thousandths
Answers
15 divided by eight and seven fifty eight thousandths will give a quotient of one and seven hundred and three thousandths
What is division operation?One of the four fundamental operations, along with addition, subtraction, and multiplication, is division. A number is split using the straightforward method of division.
The division (/) operator creates the product of its operands, where the dividend is the left operand and the divisor is the right operand.
In the problem written the words the division is done by writing in figure as below
15 ÷ 8.758
Using calculator the quotient is 1.7127 = 1.713 to the nearest thousandth
Learn more about division at:
https://brainly.com/question/25289437
#SPJ1
A man deposited 350 in his account in the bank.a simple interest of 4 percent per annum was paid on his deposit.calculate the total amount at the end of 4 years?
Answers
The total amount payable at the end of 4 years is 406
In this given sum we are provided with the values of principal , rate of interest , and the number of years , we are asked to calculate the amount payable after 4 years that is the matured amount which is calculated with the addition of the principal amount and the simple interest. For that we had to first find out the amount of interest and then we need to add that with the principal amount to get the matured amount or the amount that is payable at the end of 4 years.
here we have to apply the formulla of simmple interest :
(principal × rate of interest × no. of years )/ 100
In the given sum principal (p) = 350 , rate of interest (r) = 4% pa , no. of years (n) = 4
Simple interest = pnr/100
= (350 × 4 × 4)/100 = 56
Matured Amount = Principal + Interest
= 350 + 56 = 406
Learn more about simple interest here
https://brainly.com/question/26736329
#SPJ9
What is the equation of the line that passes through the point (5,-5) and has a slope of -1/2
Answers
Answer: y= -1/2x - 2.5
Step-by-step explanation:
Slope: y= mx+ b
m being the slope
b being the y intercept
You're given the slope, so you substitute m for -1/2
y=mx+b
y = -1/2x + b
You have the coordinates (5, -5) which you can substitute (the line passes through that point.)
-5 = -1/2(5) + b
-5 = -2.5 + b
+2.5 +2.5
-2.5= b
y= -1/2x + 2.5
Check:
-5 = -1/2(5) - 2.5
-5 = -2.5 - 2.5
-5 = -5
Ten less than 5 times the value of a number is equal to 10 times the quantity of
12 more than one-fourth of the number. If a is the number, what is the value of a?
Answers
Answer:
52
Step-by-step explanation:
given that the number is a
The expression for Ten less than 5 times the value of a number is given by
5a - 10
10 times the quantity of 12 more than one-fourth of the number.
a/4 is one-fourth of number
12 more than one-fourth of the number
a/4 + 12
expression for 10 times the quantity of 12 more than one-fourth of the number. is given by
10(a/4 + 12) = 10a/4 + 12*10 = 2.5a + 120
Given that the above two expression are equal
equating them we have
5a - 10 = 2.5a + 120
adding 10 both sides
=>5a - 10+ 10 = 2.5a + 120 + 10
=> 5a = 2.5a + 130
subtracting 2.5a from both sides
=> 5a - 2.5a = 2.5a + 130 - 2.5a
=> 2.5a = 130
dividing both side by 2.5
=> a = 130/2.5 = 52
Thus, value of a is 52
Simplify the following expression by combining like terms:
7f + 8g + 4f + 3f + 6f + 2g
Answers
Answer:
20f + 10 g or 10(2f + g)
Step-by-step explanation:
7f + 4f + 3f + 6f = 20f
2g + 8g = 10g
PLS MARK BRAINLIEST
Answer:
20f+10g
Step-by-step explanation: That was actually really easy
easy points! 35 points and brainliest!


Answers
Answer:
B
Step-by-step explanation:
( so sorry if it's wrong)
A baker would like to store 12 and 3/4 pounds of flour in containers that each hold 3 1/2 pounds of flour. How many containers will the baker need? Explain by completing the equation.
Answers
Answer:
4
Step-by-step explanation:
Because he has to store it all and not all would fit in the third container.
Expand and simplify 3(y+2)+4(x-1)
Answers
Answer:
4x + 3y + 2
Step-by-step explanation:
3(y + 2) + 4(x - 1)
3y + 6 + 4x - 4
4x + 3y + 2
Solve. If there is more than one solution, separate them with a comma.
6+3 |8x−9| =21
Answers
When something is refracted, it changes
direction
volume
size
Answers
Refraction is an effect that occurs when a light wave, incident at an angle away from the normal, passes a boundary from one medium into another in which there is a change in velocity of the light. Light is refracted when it crosses the interface from air into glass in which it moves more slowly.
prove the identity of sin(x+y)-sin(x-y)=2 cos(x) sin(y)
Answers
Answer: I dont have one for sure but I can explain why this is true.
Step by Step:
sin(x+y)−sin(x−y)=sinxcosy+sinycosx−(sinxcosy−sinycosx)
=sinxcosy+sinycosx−sinxcosy+sinycosx
=sinxcosy+sinycosx−sinxcosy+sinycosx
=sinycosx+sinycosx
=2sinycosx
henceforth proved.
Solid metal support poles in the form of right cylinders are made out of metal with a density of 6.6 g/cm^3
This metal can be purchased for $0.78 per kilogram. Calculate the cost of a utility pole with a radius of 16.2 cm and a height of 710 cm. Round your answer to the nearest cent. (Note: the diagram is not drawn to scale)
Answers
Answer:
Step-by-step explanation:
The first step is to calculate the volume of the cylinder:
Volume = π x (radius)^2 x height
Volume = π x (16.2 cm)^2 x 710 cm
Volume ≈ 1.468 x 10^6 cm^3
Next, we can calculate the mass of the metal required to make the pole:
Mass = Density x Volume
Mass = 6.6 g/cm^3 x 1.468 x 10^6 cm^3
Mass ≈ 9.6948 x 10^6 g or 9694.8 kg
Finally, we can calculate the cost of the metal required:
Cost = Price per unit mass x Mass
Cost = $0.78/kg x 9694.8 kg
Cost ≈ $7,561.17
Therefore, the cost of the utility pole would be approximately $7,561.17, rounded to the nearest cent.
Find the average value of f(x) = √81 -x² over the interval [0, 9].
![Find the average value of f(x) = 81 -x over the interval [0, 9].](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/7zLC2NSi5PriIQ6d5f3GeEREWvcC62qf.png)
Answers
Answer:
\(f_{ave}=\dfrac{9\pi}{4}\)
Step-by-step explanation:
You want the average value of f(x) = √(81 -x²) on the interval [0, 9].
AreaThe function f(x) defines a quarter circle of radius 9 in the first quadrant on the given interval. Its area is given by the formula in the problem statement:
A = (1/4)πr² = (π/4)·81
Average valueThe average value of the function is the area divided by the width of the interval:
\(f_{ave}=\dfrac{\dfrac{81\pi}{4}}{9}\\\\\\\boxed{f_{ave}=\dfrac{9\pi}{4}}\)
__
Additional comment
You will notice that the average value is π/4 times the radius. This is also true for a semicircle. The attachment shows the rectangle with area equal to that of the quarter circle.
<95141404393>
![Find the average value of f(x) = 81 -x over the interval [0, 9].](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/XeHJ70Usj9d0eKMbDGZbJ3quntpiqYER.png)
WILL GIVE BRAINLIEST! How many possibilities of HELPS are there?

Answers
Answer:
8 helpd
Step-by-step explanation:
i know it iv had probability b4
Chay is buying mulch for the zoo's summer flower beds. She has enough in her budget to purchase 55 bags of mulch. If there are 20 flower beds, how many bags of mulch can be used in each flower bed?
Answers
Chay can use 3 bags of mulch per flower bed.
Chay is buying mulch for the zoo's summer flower beds. She has enough in her budget to purchase 55 bags of mulch. If there are 20 flower beds, how many bags of mulch can be used in each flower bed?The number of bags of mulch that can be used in each flower bed can be found by dividing the total number of bags of mulch by the number of flower beds, as given by the problem.Let X be the number of bags of mulch used in each flower bed. Then, the following equation can be written:Total number of bags of mulch = X × number of flower beds (20)Or, 55 = 20XDividing both sides of the equation by 20, we get: X = 55/20X = 2.75.Therefore, Chay can use 2.75 bags of mulch in each flower bed. However, since we cannot have a fraction of a bag of mulch, she would have to round up to 3 bags of mulch per flower bed to ensure each flower bed has enough mulch.
For more such questions on flower
https://brainly.com/question/30256774
#SPJ8
Which angle number represents SXU?

Answers
Answer:
Angle 2
Step-by-step explanation:
Find S and find X.
Then find U.
The angle at X connected to S and U is the angle number.