Answers
Answer:
Step-by-step explanation:
As per midsegment theorem of a trapezoid,
Segment joining the midpoints of the legs of the of the trapezoid is parallel to the bases and measure half of their sum.
Length of midsegment = \(\frac{1}{2}(b_1+b_2)\)
3). MN = \(\frac{1}{2}(18+10)\)
= 14
4). MN = \(\frac{1}{2}(57+76)\)
= 66.5
5). MN = \(\frac{1}{2}(AB+DC)\)
7 = \(\frac{1}{2}(AB+10)\)
14 = AB + 10
AB = 14 - 10
AB = 4
6). 15 = \(\frac{1}{2}[(3x+2)+(2x-2)]\)
30 = 5x
x = 6
Related Questions
SOMEONE PLS HELP ME I WILL MAKE U BRAINLIST ! In a survey sample of 83 respondents, about 30.1 percent of the samplework less than 40 hours per week. What is the estimated standard error for the group of respondents who work 40 hours or more per week?
(*round to two decimal places)
Answers
Answer:
Answer = √(0.301 × 0.699 / 83) ≈ 0.050
A 68 percent confidence interval for the proportion of persons who work less than 40 hours per week is (0.251, 0.351), or equivalently (25.1%, 35.1%)
Step-by-step explanation:
√(0.301 × 0.699 / 83) ≈ 0.050
We have a large sample size of n = 83 respondents. Let p be the true proportion of persons who work less than 40 hours per week. A point estimate of p is because about 30.1 percent of the sample work less than 40 hours per week. We can estimate the standard deviation of as . A confidence interval is given by , then, a 68% confidence interval is , i.e., , i.e., (0.251, 0.351). is the value that satisfies that there is an area of 0.16 above this and under the standard normal curve.The standard error for a proportion is √(pq/n), where q=1−p.
Hope this answer helps you :)
Have a great day
Mark brainliest
PLEASE HELP!!!!!!!!!!!!!

Answers
Hope this helps!
A train travels 165 km in 1.5 hours.
How far will the train travel in 2.2 hours if it maintains the same speed?
Answers
\(\huge\red{\mid{\underline{\overline{\textbf{EQUATION AND ANSWER}}}\mid}}\)
_________________
Let's solve this equation using rates,
_________________DefinitionsUnit Rate - A unit rate means a rate for one of something.
Cross Multiplication - In mathematics, specifically in elementary arithmetic and elementary algebra, given an equation between two fractions or rational expressions, one can cross-multiply to simplify the equation or determine the value of a variable.
_________________
Now that we understand the definition we can further solve this equation
\(\large\red{\mid{\underline{\overline{\textbf{Values}}}\mid}}\)
\(165\) \(km\) ⇒ \(1.5\) \(hr\)
\(x\\\) \(km\) ⇒ \(2.2\) \(hr\)
Now we will use cross-multiplication to solve this equation
\(\large\red{\mid{\underline{\overline{\textbf{Equtation}}}\mid}}\)
\(165 \cdot 2.2\\x\cdot1.5\)
Once solving this equation we get
\(1.5x=363\) \(km\)
Divide both sides by \(1.5\)
\(x=242\) \(km\)
\(\large\red{\mid{\underline{\overline{\textbf{Answer}}}\mid}}\)
A train travels 165 km in 1.5 hours. How far will the train travel in 2.2 hours if it maintains the same speed?The train would've traveled a total of 242 km in 2.2 hours.
Have a good day!Write (3-2i)^3 in simplest a + bi form.
Answers
SOLUTION
We want to write
\(\begin{gathered} \mleft(3-2i\mright)^3\text{ in simplest form } \\ a+bi \end{gathered}\)This means we have to expand
\((3-2i)^3\)Applying perfect cube formula, we have
\(\begin{gathered} \mleft(a-b\mright)^3=a^3-3a^2b+3ab^2-b^3 \\ \text{where } \\ a=3,\: \: b=2i \end{gathered}\)We have
\(\begin{gathered} (a-b)^3=a^3-3a^2b+3ab^2-b^3 \\ \mleft(3-2i\mright)^3=3^3-(3\times3^2\times2i)+(3\times3\times(2i)^2)-(2i)^3_{} \\ =27-(27\times2i)+(9\times(2i)^2)-(2i)^3_{} \end{gathered}\)This becomes
\(\begin{gathered} \text{note that i = }\sqrt[]{-1} \\ i^2=\sqrt[]{-1^2}=-1 \\ So\text{ we have } \\ =27-(27\times2i)+(9\times(2i)^2)-(2i)^3_{} \\ 27-54i+(9\times4i^2)-(8i^2\times i) \\ 27-54i+(9\times4\times-1)-(8\times-1\times i) \\ 27-54i-36+8i \\ -9-46i \end{gathered}\)Hence the answer is
\(-9-46i\)Answer of question 3 pls

Answers
The highest point for the quadratic function for the height of the object, h(t) = -16·t² + 224·t + 816, indicates that the interval over which the height of the object is increasing is; (-∞, 7]
What is the shape of the graph of a quadratic function?The shape of the graph of a quadratic function is a parabola.
The function for the height of the object in question 3 is; h(t) = -16·t² + 224·t + 816
Where;
t = The time in seconds
The height of the object is increasing in the interval to the left of the highest point, which can be found as follows;
The x-coordinate of the highest point of the quadratic function, f(x) = a·x² + b·x + c is; x = -b/(2·a)
Therefore, the x-coordinates of the highest point of the object is; -224/(2 × (-16)) = 7
Therefore, the height of the object is increasing in the interval; -∞ < t ≤ 7
Learn more on quadratic functions here: https://brainly.com/question/27920694
#SPJ1
how oes the relationship between logarithms and exponential functions help us find solutions

Answers
The relationship between logarithms and exponential functions is fundamental and provides a powerful tool for finding solutions in various mathematical and scientific contexts.
Logarithms are the inverse functions of exponential functions. They allow us to solve equations and manipulate exponential expressions in a more manageable way. By taking the logarithm of both sides of an exponential equation, we can convert it into a linear equation, which is often easier to solve.
One of the key properties of logarithms is the ability to condense multiplication and division operations into addition and subtraction operations. For example, the logarithm of a product is equal to the sum of the logarithms, and the logarithm of a quotient is equal to the difference of the logarithms.
Logarithms also help us solve equations involving exponential growth or decay. By taking the logarithm of both sides of an exponential growth or decay equation, we can isolate the exponent and solve for the unknown variable.
This is particularly useful in fields such as finance, population modeling, and radioactive decay, where exponential functions are commonly used.
Furthermore, logarithms provide a way to express very large or very small numbers in a more manageable form. The logarithmic scale allows us to compress a wide range of values into a smaller range, making it easier to analyze and compare data.
In summary, the relationship between logarithms and exponential functions enables us to simplify and solve equations involving exponential expressions, model exponential growth or decay, and manipulate large or small numbers more effectively.
For more such question on logarithms visit:
https://brainly.com/question/25993029
#SPJ8
Simplfy completely (6x − 2)(6x + 2). Show all work for full credit.
Answers
Answer:
there you go. hope this helps out

Answer:
36\(x^{2}\) - 4
Step-by-step explanation:
(6x - 2)(6x + 2)
= (6x)(6x) + (6x)(-2) + (2)(6x) + (-2)(2)
= 36\(x^{2}\) - 12x + 12x - 4
= 36\(x^{2}\) - 4
A solid figure is separated into 2 rectangular prisms. The volume of rectangular prism A is 75 cubic yards. Rectangular prism
B has a length of 7 yards and a width of 3 yards. The total volume of the solid figure is 180 cubic yards. What is the height of
rectangular prism B?
Answers
The height of rectangular prism B is 5 yards.
Let's first find the volume of rectangular prism B:
The volume of the solid figure = Volume of prism A + Volume of prism B
180 = 75 + length × width × height of prism B
105 = length × width × height of prism B
We know that the length of prism B is 7 yards and the width is 3 yards,
Substitute those values:
105 = 7 × 3 × height of prism B
105 = 21 × height of prism B
height of prism B = 105/21
height of prism B = 5
Therefore, the height of rectangular prism B is 5 yards.
To know more about rectangular prism follow
https://brainly.com/question/30799424
#SPJ1
MORE POINTS AND BRAINLIEST?!
Answers
Answer:
? hey wanna be friends?
Answer:
hi!
Step-by-step explanation:
Find the limit when X approaches zero
2xsinx/1-cosx

Answers
Answer:
4
Step-by-step explanation:
\( Lim_{x \to 0}\frac{2 x\sin x}{1-\cos x} \)
\( =Lim_{x \to 0}\frac{2 x\sin x}{1-\cos x}\times \frac{1+\cos x}{1+\cos x} \)
\( =Lim_{x \to 0}\frac{2 x\sin x(1+\cos x) }{1^2 -\cos^2 x} \)
\( =Lim_{x \to 0}\frac{2 x\sin x(1+\cos x) }{1 -\cos^2 x} \)
\( =Lim_{x \to 0}\frac{2 x\sin x(1+\cos x) }{sin^2 x} \)
\( =Lim_{x \to 0}\frac{2x(1+\cos x) }{sin x} \)
\( =Lim_{x \to 0} 2(1+\cos x) \times \frac{1}{Lim_{x \to 0}\frac{sin x}{x}} \)
\( =2(1+\cos 0) \times 1 \)
\( = 2(1+1) \)
\( = 2(2) \)
\( \therefore Lim_{x \to 0}\frac{2 x\sin x}{1-\cos x}= 4 \)
Physicians at a clinic gave what they thought were drugs to 820
patients. Although the doctors later learned that the drugs were really placebos,
52% of the patients reported an improved condition. Assume that if the placebo is ineffective, the probability of a patient's condition improving is .48
Test the hypotheses that the proportion of patients improving is >
.48
Answers
We reject the null hypothesis since the p-value is less than the significance level of 0.05.
what is null hypothesis ?The null hypothesis in statistics is a claim that presupposes there is no statistically significant distinction among the two or even more variables be compared. The antithesis of the alternative hypothesis, it is frequently denoted as H0 (Ha). While conducting statistical studies, the null is often evaluated to see if there is sufficient proof against it or not. The default assumption is typically the null hypothesis, and it serves as a benchmark for comparison of the statistical analysis's findings. A statistically significant distinction between the variables under comparison is said to exist if the statistical analysis yields sufficient data to refute a null hypothesis.
given
To test the hypothesis, we can utilise a z-test. This is the test statistic:
\(z = (x - E) / σ\)
where x is the observed percentage of patients whose conditions are getting better. x = 820 * 0.52 = 426.4 is the result. Therefore:
z = (426.4 - 393.6) / 0.026 = 1245.98
P(Z > z) = 1 - P(Z z) is the p-value for this one-tailed test, where Z is a normal standard variable. By using a typical table or calculator, we discover:
P(Z > 1245.98) < 0.0001
We reject the null hypothesis since the p-value is less than the significance level of 0.05.
We have enough data to draw the conclusion that the percentage of patients whose conditions are improving is more than 0.48.
To know more about null hypothesis visit
https://brainly.com/question/28920252
#SPJ1
Use a sum or difference identity to find the exact value.

Answers
The solution to the value \(cos\dfrac{7\pi}{12}\) will be \(\dfrac{-\sqrt{6}+\sqrt{2}}{4}\). The correct option is B.
What are trigonometric identites?Trigonometric Identities are equality statements that use trigonometry functions and hold true for all values of the variables in the equation. There are numerous distinct trigonometric identities that relate to the side length and angle of a triangle.
Use the trigonometric identity to solve the given expression as below,
Cos(a + b ) =Cos(a) Cos(b) - Sin(a)Sin(b)
We can also write the expression as,
\(cos\dfrac{7\pi}{12} = cos(\dfrac{5\pi}{12}+\dfrac{2\pi}{12})\)
Apply the formula,
Cos(a + b ) =Cos(a) Cos(b) - Sin(a)Sin(b)
\(cos(\dfrac{5\pi}{12}+\dfrac{2\pi}{12}) = cos(\dfrac{5\pi}{12})\times cos(\dfrac{2\pi}{12}) - sin(\dfrac{5\pi}{12})\times sin(\dfrac{2\pi}{12})\)
\(cos(\dfrac{5\pi}{12}+\dfrac{2\pi}{12}) =[ \dfrac{\sqrt{6}-\sqrt{2}}{4}\times -1]- 0\)
\(cos\dfrac{7\pi}{12} =cos(\dfrac{5\pi}{12}+\dfrac{2\pi}{12}) =\dfrac{-\sqrt{6}+\sqrt{2}}{4}\)
Therefore, the solution to the value \(cos\dfrac{7\pi}{12}\) will be \(\dfrac{-\sqrt{6}+\sqrt{2}}{4}\). The correct option is B.
To know more about trigonometric identity follow
brainly.com/question/7331447
#SPJ1
Given: with median segments , , and Prove: Medians meet at point O. It is given that has median segments , , and . Because ___________, then , , and . The ratios of to is 1, of to is 1, and of to is 1 by substitution. Therefore, , , and are similar to each other. Then the medians meet at point O. What is the reasoning for the second step? A. medians intersect at multiple points B. medians divide each side of the triangle into two parts C. medians intersect at one point D. medians divide each side of the triangle in half
Answers
Answer:
A:medians divide each side of the triangle in half
Step-by-step explanation:
on plato
What is the value of c?
a)4 units
b)5 units
c)6 units
d)7 units

Answers
The value of c in the triangle is (b) 5 units
Finding the value of c in the triangleFrom the question, we have the following parameters that can be used in our computation:
The right triangle
The length c is the hypotenuse of one of the triangles and can be calculated using the following Pythagoras theorem
c² = sum of squares of the legs
Using the above as a guide, we have the following:
c² = 3² + 4²
Evaluate
c² = 25
Take the square roots
c = 5
Hence, the hypotenuse of the right triangle is 5
Read more about right triangle at
https://brainly.com/question/2437195
#SPJ1
(a) You have a 10 inch by 15 inch piece of tin which you plan to form into a box (without a top) by cutting a square from each corner and folding up the sides. How much should you cut from each corner so the resulting box has the greatest volume? (b) If the piece of tin is A inches by B inches, how much should you cut from each corner so the resulting box has the greatest volume?
Answers
Resulting box has the greatest volume for the values (25 ± 5√7)/6 .
This is a problem that can be solved using derivatives , maxima & minima and common logic.
Hence , going by logic :
Creating a flap of 'a' inches in width, the base of the box will be
(10 - 2a) by (15 - 2a)
and the depth of the box will be the width of the fold-up flap: a.
Then the volume of the box is
v = \(a(10 -2a)(15 -2a) = 150a -50a^2 +4a^3\)
Using the derivative of the volume will be zero at the maximum volume.
0 = \(dv/da = 150 -100a +12a^2\)
This has roots at
a = (100 ±√(100² - 4(12)(150)))/(2·12)
a = (100 ± √2800)/24 = (25 ± 5√7)/6
Only the smaller of these solutions gives a maximum volume.
You should cut (5/6)(5-√7) ≈ 1.962 inches to obtain the greatest volume.
Similarly , replacing the values of 10 by A and 15 by B , a generalized solution can be formed .
To know more about maxima and minima, go to brainly.com/question/29562544
#SPJ4
6. Solve this system of linear equations without graphing:72 +lly = -27x + 3y = 30

Answers
SOLUTION
Write out the system of equation given
\(\begin{gathered} 7x+11y=-2 \\ 7x+3y=30 \end{gathered}\)Using eliminationm method, we subtract the equation above to eliminate y
hence
\(\begin{gathered} (7x-7x)+(11y-3y)=(-2-30) \\ 8y=-32 \end{gathered}\)Then divide both sides by 8, we have
\(\begin{gathered} \frac{8y}{8}=-\frac{32}{8} \\ \text{Then} \\ y=-4 \end{gathered}\)Hence
y = -4
The substitute the value of y into any of the equation above to obtain x, we have
\(\begin{gathered} \text{ Using the second equation, we have } \\ 7x+3y=30 \\ y=-4 \\ 7x+3(-4)=30 \\ 7x-12=30 \\ \end{gathered}\)Add 12 from both sides, we have
\(\begin{gathered} 7x-12+12=30+12 \\ 7x=42 \\ \text{Divide both sides by 7, we have } \\ \frac{7x}{7}=\frac{42}{7} \\ \text{Then} \\ x=6 \end{gathered}\)Hence
x=6
Therefore
Answer is x = 6, y = - 4
Write an equation that you can use to solve for x.
Enter your answer in the box.
Two lines intersect forming a pair of vertical angles measuring 100 degrees. A ray divides one of the 100 degree angles into two adjacent angles. One of the adjacent angles is labeled 60 degrees and the other adjacent angle is labeled x degrees.
Please hurry I will mark branliest
Answers
Answer:
x+60=100
I am in 7th grade in k12
~~ :)
Answer:
x=100-60
Step-by-step explanation:
Which formula should be used to find the circumference of a circle?
A. C = pi d
B. C = 2 pi d
C. C = pi r
D. C = pi over d
Answers
Answer:A
Step-by-step explanation:
Answer:
A is right
Step-by-step explanation:
What are the new coordinates if the figure were rotated 90 degrees counterclockwise

Answers
Answer:
third option
Step-by-step explanation:
under a counterclockwise rotation of 90° about the origin
a point (x, y ) → (y, - x )
Then
A (- 1, - 2 ) → (- 2, - (- 1) ) → (- 2, 1 )
B (2, - 2 ) → (- 2, - 2 )
C (1, - 4 ) → (- 4, - 1 )
The new coordinates are (d) A = (2, -1) B = (2, 2) and C = (4, 1)
How to determine the new coordinates rotating by 90 degrees counterclockwiseFrom the question, we have the following parameters that can be used in our computation:
The figure,
Where, we have
A = (-1, -2)
B = (2, -2)
C = (1, -4)
The rule of 90 degrees counterclockwise is
(x, y) = (-y, x)
Using the above as a guide, we have the following:
A = (2, -1)
B = (2, 2)
C = (4, 1)
Hence, the new coordinates are (d) A = (2, -1) B = (2, 2) and C = (4, 1)
Read more about transformation at
https://brainly.com/question/27224272
#SPJ1
A sunflower is measured at the beginning of June and is 40cm tall. The sunflower
grows by 25% each month for three months. What height is the sunflower to the nearest
centimetre at the beginning of September?
Answers
Answer:
78cm 78.125
Step-by-step explanation:
Answer: 78.13
Step-by-step explanation:
you start with 40cm and find 25% of that and add it to 40cm. Or you can do 1.25x40=50 That would be July, so repeat to get 50x1.25=62.5 to get august, then again to get 62.5x1.25=78.13
Allison spent a total of $16.20 for lunch including tax and a tip. She paid 8% sales tax on her purchase and then left a tip equivalent to 20% of her total bill including tax. What was the cost of Allison’s meal, before tax and tip?
Answers
Answer:good job!
Step-by-step explanation:
Step-by-step
\(2x + 3y < 45\)
Answers
Answer:
Hello!
~~~~~~~~~~~~~~~``
Simplifying
2x + 3y = 45
Solving
2x + 3y = 45
Solving for variable 'x'.
Move all terms containing x to the left, all other terms to the right.
Add '-3y' to each side of the equation.
2x + 3y + -3y = 45 + -3y
Combine like terms: 3y + -3y = 0
2x + 0 = 45 + -3y
2x = 45 + -3y
Divide each side by '2'.
x = 22.5 + -1.5y
Simplifying
x = 22.5 + -1.5y
Hope this helped you! Brainliest would be nice.
If a fruit cake needs 3 4 of a carton of all-purpose cream and 2 3 of a carton of condensed milk to make, how many cartons of all purpose cream does Grandma need to buy to make 5 fruit cakes?
Answers
2/3 * 5= 3 1/3. But you can’t buy 1/3 of a carton, so grandma needs to buy 4 cartons of condensed milk.
All together, Grandma needs to buy 4 cartons of all-purpose cream and 4 cartons of condensed milk to make 5 fruit cakes.
a) calculate the reynolds number for a sphere moving in air at 15 m/s with a diameter of 10cm. b) is this flow around the sphere turbulent? (yes/no/maybe) c) calculate the reynolds number for a sphere moving in water at 15 m/s with a diameter of 10cm.
Answers
a) The Reynolds number for a sphere moving in air is 83,333.33.
b) Yes, Based on the Reynolds number, the flow around the sphere is turbulent (Re > 4000).
c) The Reynolds number for a sphere moving in water is 150,000.
Reynolds Number Sphere Flowa) To calculate the Reynolds number for a sphere moving in air at 15 m/s with a diameter of 10cm, we can use the formula:
Re = (density * velocity * diameter) / viscosity
Where density of air is 1.2 kg/m³, viscosity of air is 1.78 x 10⁻⁵ Ns/m² and diameter is 0.1m.
Re = (1.2 * 15 * 0.1) / (1.78 x 10⁻⁵)
Re = 83333.33
b) Based on the Reynolds number, the flow around the sphere is turbulent (Re > 4000). So, the answer is yes.
c) To calculate the Reynolds number for a sphere moving in water at 15 m/s with a diameter of 10cm, we can use the formula:
Re = (density * velocity * diameter) / viscosity
Where density of water is 1000 kg/m³ and viscosity of water is 0.001 Ns/m².
Re = (1000 * 15 * 0.1) / (0.001)
Re = 150000
Based on the Reynolds number, the flow around the sphere is turbulent (Re > 4000).
Learn more about Reynolds Number Sphere Flow here:
https://brainly.com/question/12977616
#SPJ4
Enter the number that belongs in the green box
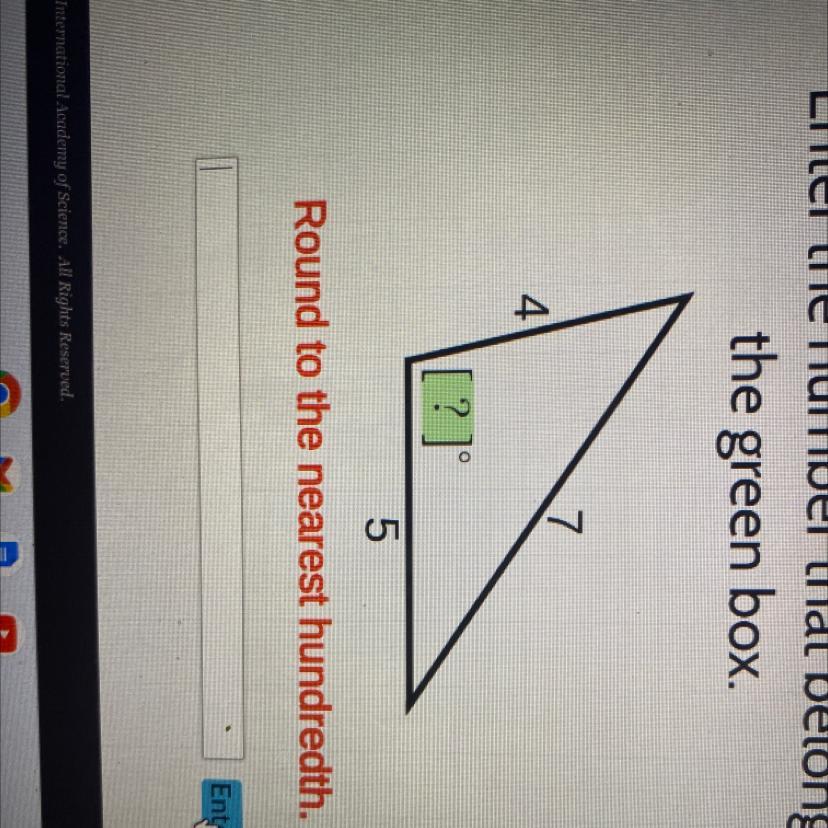
Answers
The angle between the sides measuring 4 and 5 in the obtuse triangle is approximately 101.54 degrees.
To find the measure of the angle between the sides measuring 4 and 5 in an obtuse triangle with side lengths 4, 5, and 7, we can use the Law of Cosines. The Law of Cosines states that in a triangle with side lengths a, b, and c, and an angle opposite to side c, the following equation holds:
\(c^2 = a^2 + b^2 - 2ab*cos(C)\)
In this case, we have side lengths a = 4, b = 5, and c = 7. We want to find the angle C, which is opposite to side c. Substituting these values into the Law of Cosines, we get:
\(7^2 = 4^2 + 5^2\)- 2(4)(5)*cos(C)
49 = 16 + 25 - 40*cos(C)
49 = 41 - 40*cos(C)
40*cos(C) = 41 - 49
40*cos(C) = -8
cos(C) = -8/40
cos(C) = -0.2
To find the measure of angle C, we can take the inverse cosine (arccos) of -0.2:
C = arccos(-0.2)
Using a calculator, we find that C ≈ 101.54 degrees.
Therefore, the measure of the angle between the sides measuring 4 and 5 in the obtuse triangle is approximately 101.54 degrees.
For more such information on: angle
https://brainly.com/question/25716982
#SPJ8
write a polynomial that represents the area of the square

Answers
Answer:
y = x² + 8x + 16
Step-by-step explanation:
blue square = x × x = x²
green rectangle = 4 × x = 4x
yellow square = 4 × 4 = 16
Let y = total area of the square
⇒ y = blue square + green rectangle + green rectangle + yellow square
= x² + 4x + 4x + 16
= x² + 8x + 16
Area:-
side²(x+4)²x²+8x+16units²Help 50 points (show ur work)



Answers
1. The value of 34% of 850 is 289.
3. The amount that Kepley paid for the tool is $120.
How to calculate the value?From the information, we want to calculate 34% of 850. This will be calculated thus:
= 34% ×850
= 34/100 × 850
= 0.34 × 850
= 289
The amount paid for the tool will be:
= Price or tool - Discount
= $200 - (40% × $200)
= $200 - $80
= $120
Learn more about percentages on:
brainly.com/question/24304697
#SPJ1
Math Homework: Unit 3 Assignment

Answers
What’s the mean of 46,57,66,63,49,52,61,68
Answers
Answer:
Step-byHow do I calculate the mean?
The mean can be calculated only for numeric variables, no matter if they are discrete or continuous. It's obtained by simply dividing the sum of all values in a data set by the number of value
-step explanation:
46+57+66+63+49+52+61+68= 462/8 the total number of observation
the answer 57
the answer 57
For the function, find f (−2), f (−0.5), and f (3).
f(x) = −5x + 2
Answers
Answer:
2
Step-by-step explanation:
becaue i siad so
