HELP PLEASE 45pts (WILL GIVE BRANLIEST!!!!)
How do you determine the scale factor of a dilation? Explain in general and with at least one example.
How do you determine if polygons are similar? Explain in general and give at least one example
Answers
If AB/DE = BC/EF = AC/DF, then triangle ABC is similar to triangle DEF.
To determine the scale factor of a dilation, you need to compare the corresponding lengths of the pre-image and image of a figure. The scale factor is the ratio of the lengths of any two corresponding sides.
For example, suppose you have a triangle ABC with sides AB = 3 cm, BC = 4 cm, and AC = 5 cm. If you dilate the triangle by a scale factor of 2, you get a new triangle A'B'C'.
To find the length of A'B', you multiply the length of AB by the scale factor: A'B' = 2 * AB = 2 * 3 = 6 cm. Similarly, B'C' = 2 * BC = 2 * 4 = 8 cm and A'C' = 2 * AC = 2 * 5 = 10 cm. Therefore, the scale factor of the dilation is 2.
To determine if polygons are similar, you need to check if their corresponding angles are congruent and their corresponding sides are proportional.
In other words, if you can transform one polygon into another by a combination of translations, rotations, reflections, and dilations, then they are similar.
For example, suppose you have two triangles ABC and DEF.
If angle A is congruent to angle D, angle B is congruent to angle E, and angle C is congruent to angle F, and the ratios of the lengths of the corresponding sides are equal, then the triangles are similar. That is, if AB/DE = BC/EF = AC/DF, then triangle ABC is similar to triangle DEF.
To know more about triangles refer here:
https://brainly.com/question/2773823
#SPJ11
Related Questions
jill and joel wrote equations for the line passing through the points (2,-1) and (-1,14). which student is correctJill 5x + y = 9Joel y + 1 = -5(x-2)a. jill only b. joel only c. both d. neither
Answers
The equation given by Jill and Joel both are correct. Option C .
The line passing through the points (2, -1) and (-1, 14).
The equation of a line passing through a point \((x_1, y_1)\) is \(y-y_1=m (x-x_1)\) where m is the slope.
To find the slope m, using slope formula.
\(m=\frac{y_2-y_1}{x_2-x_1} \\m=\frac{14-(-1)}{-1-3} \\m=-5\)
Further simplify,
Substitute the values in the given formula.
\(y-y_1=m(x-x_1)\\y-(-1)=-5(x-2)\\y+1=-5(x-2)\)
Further simplify,
5x+y=9
Both the equations are correct.
To learn more about slope refer the link:
https://brainly.com/question/3605446
#SPJ4
HELP MEE PLSSS
Uncle Drew scored 282828 points in 5\dfrac565
6
5
5, start fraction, 5, divided by, 6, end fraction minutes during a game of basketball.
How many points did he average per minute during that 5\dfrac565
6
5
5, start fraction, 5, divided by, 6, end fraction minutes?
points per minute
Answers
Answer:
i do no
Step-by-step explanation:
PLEASE HELP QUICK AHHHH <333

Answers
Answer:
=> ( -6,-10 )Step-by-step explanation:
Given :
x = -6
-7x + 6y = -18 ... i)
Putting the value of x in equation ...i)
=> -7 (-6) + 6y = -18
=> 42 + 6y = -18
=> 6y = -18 -42
=> 6y = - 60
=> y = -60/6
=> y = -10
The value of y = -10 and x = -6
Answer:
x= 4, y=6
Step-by-step explanation:
9x-9y = -18
9x=-18+9y
x=-2+y
-6(-2+y) + 9y = 6
-12-6y+9y=6
3y=18
y=6
9x -9(6)=-18
9x-54=-16
9x=36
x=4
A recipe requires 34 cups of milk. Paula is making 12 of the recipe. How many cups of milk will Paula use?
Answers
Three different ways to name the shaded angles are

Answers
Let f(x) = x²+1 and g(x)=3 x . Evaluate each expression. (g ₀ f) (1/2)
Answers
The value of the expression (g ₀ f) (1/2) is 15/4
In this question, we have been given two functions f(x) = x² + 1 and g(x) = 3x.
We need to evaluate an expression. (g ₀ f) (1/2)
We know that the composite function is a function where the output of one function becomes the input of another function.
First we find the composite function (g ₀ f) (x)
(g ₀ f) (x)
= g(f(x))
= 3(f(x))
= 3 (x² + 1 )
= 3x² + 3
So, (g ₀ f) (x) = 3x² + 3
Now, we find the value (g ₀ f) (1/2)
(g ₀ f) (1/2)
= 3(1/2)² + 3
= 3(1/4) + 3
= 3/4 + 3
= 15/4
Therefore, the value of the expression (g ₀ f) (1/2) is 15/4
Learn more about the composite function here:
https://brainly.com/question/20379727
#SPJ4
There are 2 different questions please help me!!!!!!!!!


Answers
The required point that lies in the solution of the given inequality is (7, 2). Option D is correct.
Given that,
Two pair of inequality is given 4x + 2y > 8 and x - y ≥ 2.
The graph is a demonstration of curves that gives the relationship between the x and y-axis.
Here,
4x + 2y > 8 - - - - - (1)
x - y ≥ 2 - - - - - - (2)
Plotting the graph of both the inequality to determine the points that lies in the solution.
From comparing the solution the pair is (7, 2).
Thus, the required point that lies in the solution of the given inequality is (7, 2). Option D is correct.
Learn more about graphs here:
brainly.com/question/16608196
#SPJ1

Find the value of x in the figure: SHOW YOUR WORK so I can see if the answer makes sense (no links)

Answers
Triangles ABC and ADE are similar (side-angle-side postulate) in a ratio of 2 to 1. This means triangle ABC is 2 times larger than triangle ADE.
This in turn means that BC is twice as long as DE, so
4x - 6 = 2 (x + 1)
Solve for x :
4x - 6 = 2x + 2
4x - 2x = 2 + 6
2x = 8
x = 4
I need help with this please. What’s the answer?
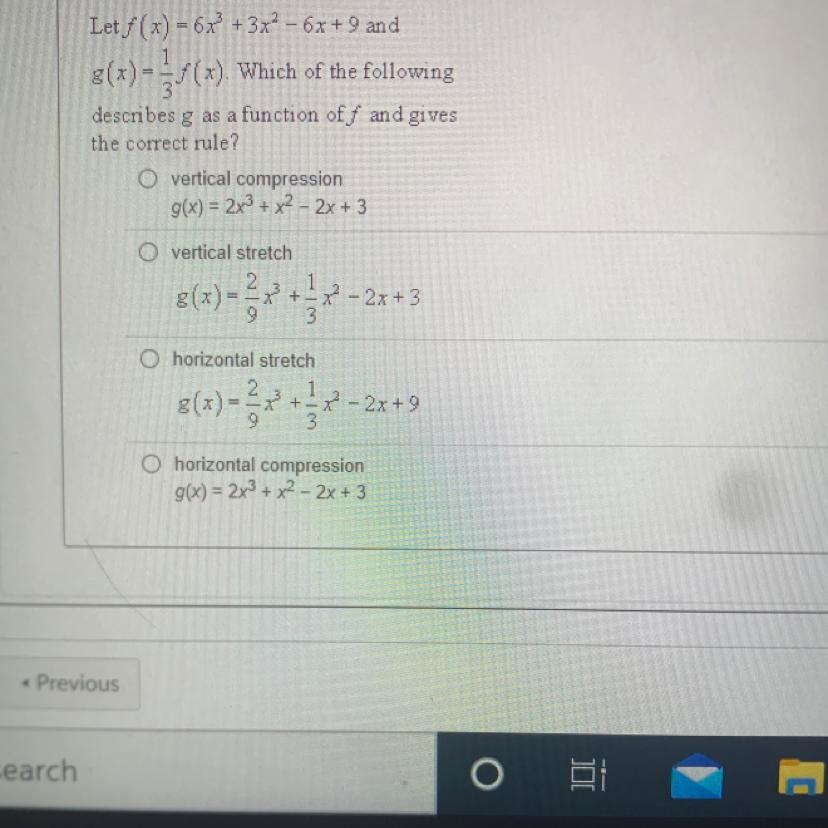
Answers
Answer:
I believe the answer to this question is A.
Step-by-step explanation:
In order to find the right polynomial, we had to input the value of f(x) into the function g(x) and multiply it out:
g(x) = 1/3(6x^3 + 3x^2 - 6x + 9)
g(x) = 2x^3 + x^2 - 2x + 3
Now, this polynomial would be a vertical compression because we are multiplying the polynomial by a fraction (1/3).
statistical power is a measure of the ability to reject the null hypothesis when:
Answers
Statistical power is a measure of the ability to reject the null hypothesis when it is false. It represents the probability of correctly identifying a true effect or relationship in a statistical hypothesis test.
A high statistical power indicates a greater likelihood of detecting a significant result if the null hypothesis is indeed incorrect. The power of a statistical test depends on several factors, including the sample size, the effect size (the magnitude of the true effect or difference), the chosen significance level (often denoted as α), and the variability or noise in the data. Increasing the sample size or effect size generally increases the statistical power, while a lower significance level or higher variability decreases it.
Power analysis is commonly used to determine an appropriate sample size for a study, ensuring that it is adequately powered to detect the desired effect. A higher power is desirable as it reduces the chances of a Type II error (failing to reject the null hypothesis when it is false) and increases the chances of correctly detecting real effects or relationships.
Learn more about null hypothesis here:
https://brainly.com/question/29387900
#SPJ11
A researcher is told that the average age of respondents in a survey is 49 years. She is interested in finding out if most respondents are close to 49 years old. The measure that would most accurately answer this question is: a. mean. b. median. c. mode. d. range. e. standard deviation.
Answers
The researcher should use the measure of e. standard deviation. This is because standard deviation provides an indication of the dispersion or spread of the data around the mean.
Helping to understand how close the ages are to the average (49 years).The measure that would most accurately answer the researcher's question is the median. The median is the middle value in a dataset, so if most respondents are close to 49 years old, the median would also be close to 49 years old.
The mean could also be used to answer this question, but it could be skewed if there are outliers in the dataset. The mode, range, and standard deviation are not as useful in determining if most respondents are close to 49 years old.
To know more about median visit:-
https://brainly.com/question/300591
#SPJ11
I've been stuck on this question. if you can help me out that will be awesome :D
(picture is the problem)

Answers
Answer:
5 Units!
Step-by-step explanation:
Give Brainiest answer to me! :D I neeeed itttt
if x=3 and y=8, then the value of 5xy is
Answers
Answer:120
Step-by-step explanation:
given x= 3 and y= 8,
we have to find the value of 5xy
so let us put the values of x and y in the given expression i.e 5xy.2
= 5×3×8
= 120
Hence the value of 5 xy is 120.
Answer:
Step-by-step explanation:
If x = 3 and y = 8, then the value of 5xy is simply 5 times the product of x and y.
To find the product of x and y, we simply multiply x and y together:
xy = 3 * 8 = 24
To find the value of 5xy, we simply multiply 5 by the value of xy:
5xy = 5 * 24 = 120
So the value of 5xy when x = 3 and y = 8 is 120
whats the answer its really annoying not gonna lie

Answers
Answer:
22
Step-by-step explanation:
4*4=16
4*2=8/2=4
4*1=4/2=2
16+4+2=22
Solve the augmented matrix by elementary row operations. 9. (4 points) Let A and B be 3 by 3 matrices with det (A) = 3 and det (b) = 5. Find the value of det (AB).
Answers
The value of determinant of the matrix det (AB) is 15.
Given matrices A and B are 3 by 3 matrices with
det (A) = 3 and
det (b) = 5.
We need to find the value of det (AB).
Writing the given matrices into the augmented matrix form gives [A | I] and [B | I] respectively.
By multiplying A and B, we get AB. Similarly, by multiplying I and I, we get I. We can then write AB into an augmented matrix form as [AB | I].
Therefore, we can solve the augmented matrix [AB | I] by row reducing [A | I] and [B | I] simultaneously using elementary row operations as shown below.

The determinant of AB can be calculated as det(AB) = det(A) × det(B)
= 3 × 5
= 15.
Conclusion: The value of det (AB) is 15.
To know more about determinant visit
https://brainly.com/question/11841826
#SPJ11
We need to find the value of determinant det(AB), using the formula: det(AB) = det(A)det(B)
=> det(AB) = 3 × 5
=> det(AB) = 15.
Hence, the value of det(AB) is 15.
The given matrices are A and B. Here, we need to determine the value of det(AB). To calculate the determinant of the product of two matrices, we can follow this rule:
det(AB) = det(A)det(B).
Given that: det(A) = 3
det(B) = 5
Now, let C = AB be the matrix product. Then,
det(C) = det(AB).
To evaluate det(C), we have to compute C first. We can use the following method to solve the augmented matrix by elementary row operations.
Given matrices A and B are: Matrix A and B:
[A|B] = [3 0 0|1 0 1] [0 3 0|0 1 1] [0 0 3|1 1 0][A|B]
= [3 0 0|1 0 1] [0 3 0|0 1 1] [0 0 3|1 1 0].
We can see that the coefficient matrix is an identity matrix. So, we can directly evaluate the determinant of A to be 3.
det(A) = 3.
Therefore, det(AB) = det(A)det(B)
= 3 × 5
= 15.
Conclusion: Therefore, the value of det(AB) is 15.
To know more about determinant visit
https://brainly.com/question/11843479
#SPJ11
2x + 10 - 8x = -38
2(x + 5) = -2
-10 = -5(x +9)
6 - 7x - 19 = -83
3(3x - 4) = 24
can anybody help me on all of these questions? quick and thank you so much!
Answers
Answer:
x = 8x = -6x = -7x = 10x = 4Step-by-step explanation:
1. 2x+10-8x = -38
-6x + 10 = -38
-6x = - 48
x = 8
2. 2(x+5)=-2
2x + 10 = -2
2x = -12
x= -6
3. -10 = -5(x+9)
-10 = -5x - 45
35 = -5x
x = -7
4. 6 - 7x - 19 = -83
-13 - 7x = -83
-7x = -70
x = 10
5. 3(3x-4) = 24
9x - 12 = 24
9x = 36
x = 4
Please help!! 15 points

Answers
(I’m going to be using the first x value in the data table but any value will work.)
Y = 5x: Y= 5*5 which is 25 ❌And in the data table $5 is supposed to equal the y value of 0.41 so keep trying the other equations
Y = 10.82x: Y= 10.82*5 which is 54.1 ❌
Y = 0.41x: Y= 0.41*5 which is 2.05 ❌
Y = 0.082x: Y = 0.082*5 = 0.41 ✅
Now finally, check your answer by using another value in the data table and substituting it in the answer you believe is correct
Y = 0.082x = 0.082*10 which is 0.82.
This answer seems to hold true so I believe it is D: Y = 0.082x
I apologize if this is wrong and if you have any questions please ask me.
What is the percent of change from
65 to 52?
Round to the nearest percent.
Answers
Answer:
20%
Step-by-step explanation:
\(\frac{52-65}{65}\) * 100% = -20%
I have sent a picture of the question I’m needing help with. Thank you

Answers
We know that:
- the height in feet t seconds after launch is given by
\(s=-16t^2+v_0t\)And we must find the times that the projectil will reach a height of 80ft and when v0 = 96 feet per second
To find it we need to replace s = 80 and v0 = 96 in the formula
\(80=-16t^2+96t\)Then, we must solve the equation for t
1. we must move all terms aside
\(80+16t^2-96t=0\)2. we must extract the common factor 16
\(16(5+t^2-6t)=0\)3. we must factor
\(16(t-5)(t-1)=0\)4. we must solve for t
We have two possible results
\(\begin{gathered} 1. \\ 16(t-5)(t-1)=0 \\ t-5=0 \\ t=5 \\ 2. \\ 16(t-5)(t-1)=0 \\ t-1=0 \\ t=1 \end{gathered}\)ANSWER:
A. 1, 5 seconds
Problem #5: Let A and B be nxn matrices. Which of the following statements are always true? (i) If det(A) = det(B) then det(A - B) = 0. (ii) If A and B are symmetric, then the matrix AB is also symmet
Answers
Numbers, symbols, or expressions are arranged in rows and columns in rectangular arrays known as matrices.
They are extensively utilized in many branches of mathematics, including statistics, calculus, and linear algebra, as well as in other disciplines including physics, computer science, and economics. Both statements (i) and (ii) are False.
(i) If det(A) = det(B) then det(A - B) = 0.The statement is not true because if det(A) = det(B) and A - B is a singular matrix, then
det(A - B) ≠ 0.For example, take
A = [1 0; 0 1] and
B = [2 1; 1 2].
Here, det(A) = det(B) = 1, but det(A - B) = det([-1 -1; -1 -1]) = 0.
(ii) If A and B are symmetric, then the matrix AB is also symmetric. The statement is not true because in general AB ≠ BA, unless A and B commute. Therefore, if A and B are not commuting matrices, then AB is not symmetric. For example, take
A = [0 1; 1 0] and
B = [1 0; 0 2]. Here, both A and B are symmetric matrices, but
AB = [0 2; 1 0] ≠ BA. Therefore, AB is not a symmetric matrix.
To know more about Matrices visit:
https://brainly.com/question/21137583
#SPJ11
(b) If you put $9050 in the ATM each day, what percent of the days in a month should
you expect to run out of cash?
Answers
Answer:
23.33%
Step-by-step explanation:
The computation of the percentage of days in a month for running out of cash is shown below:
Percentage of running out of Cash is
= (Relevant Occurrence of an event ÷ Total number of events) × 100%
where,
The Relevant occurrence of an event is 7 (105,94,101,98,94,96,92)
And, the total number of events is 30 i.e. 30 days
So, the percentage is
= 7 ÷ 30 × 100
= 23.33%

Solveeeee!!!!!!iiippp

Answers
the answer is less than 1/8 of a pizza. 1/4 divided by 6 = 1/4 x 1/6 = 1/24
and it is less than 1/8, pretty obvious.
pls help i am speedrunning overdues rn

Answers
The amount of soil needed to fill the garden box is given as follows:
1728 ft³.
How to obtain the volume of a rectangular prism?The volume of a rectangular prism, with dimensions defined as length, width and height, is given by the multiplication of these three defined dimensions, according to the equation presented as follows:
Volume = length x width x height.
The figure in this problem is composed by two prisms, with dimensions given as follows:
19 ft, 12 ft and 6 ft.10 ft, 3 ft and 12 ft.Hence the volume is given as follows:
V = 19 x 12 x 6 + 10 x 3 x 12
V = 1728 ft³.
More can be learned about the volume of a rectangular prism at brainly.com/question/22070273
#SPJ1
Find the perimeter of the window to the nearest tenth.
A semi-circular windowpane with radius labeled 20 centimeters
Answers
Answer:
102.8 cm
Step-by-step explanation:
The perimeter of a semicircle is the sum of the length of the diameter and the length of the curved edge. The curved edge is half the circumference of a circle with the same radius.
perimeter = diameter + curved edge
= 2r +1/2(2πr) = r(2 +π)
= (20 cm)(2 +π) ≈ 102.8 cm
The perimeter of the window is about 102.8 cm.
Approximate the value of the series to within an error of at most 10^(−5).
[infinity]∑n=1 (−1)^(n+1)/n^7
According to Equation (2):
|SN−S|≤aN+1
what is the smallest value of N that approximates S to within an error of at most 10^(−5)?
N=
S≈
Answers
the approximation of S is approximately -0.992583715.
To approximate the value of the series within an error of at most 10^(-5), we need to find the smallest value of N that satisfies the inequality:
|SN - S| ≤ aN+1
where SN represents the partial sum of the series up to the Nth term, S represents the actual sum of the series, and aN+1 represents the error bound.
For the given series:
∑(n=1 to ∞) (-1)^(n+1)/n^7
The general term of the series can be written as:
an = (-1)^(n+1)/n^7
To approximate S within an error of at most 10^(-5), we need to find the smallest N such that aN+1 ≤ 10^(-5).
Let's calculate the terms until we find the first term that satisfies the inequality:
a1 = (-1)^(1+1)/1^7 = -1
a2 = (-1)^(2+1)/2^7 = 1/128 ≈ 0.0078125
a3 = (-1)^(3+1)/3^7 = -1/2187 ≈ -0.00045725
a4 = (-1)^(4+1)/4^7 = 1/16384 ≈ 0.000061035
...
By calculating subsequent terms, we find that a4 ≈ 0.000061035 is the first term that is less than or equal to 10^(-5).
Therefore, the smallest value of N that approximates S to within an error of at most 10^(-5) is N = 4.
To find the approximation of S, we calculate the partial sum up to the 4th term:
S ≈ a1 + a2 + a3 + a4
≈ -1 + 0.0078125 - 0.00045725 + 0.000061035
≈ -0.992583715
the approximation of S is approximately -0.992583715.
to know more about series visit:
brainly.com/question/15692483
#SPJ11
in a standard deck of 52 cards, how many cards must be picked to be sure that - at least five of them are spades
Answers
Answer:
44 cards
Step-by-step explanation:
In a standard deck of 52 cards, there are 4 suits each of which has 13 cards. Since we are finding the minimum value to be fully guaranteed of drawing five spades we can assume the scenario as follows:
If the first 39 cards picked are the complete full suits of hearts, diamonds, and clubs, then we know that the next 13 are spades. Since we have to find at least five spades we add 5 cards to the 39 to get our answer of 44 cards to be absolutely guaranteed.
A classroom had 42 glue sticks. If the ratio of glue sticks to glue bottles was 7 : 4, how many glue bottles did the classroom have?
Answers
The classroom had 24 glue bottles.
We have,
If the ratio of glue sticks to glue bottles is 7 : 4, we can express this as 7/4.
We can set up a proportion to solve for the number of glue bottles:
7/4 = 42/x
where x is the number of glue bottles. To solve for x, we can cross-multiply:
7x = 4 x 42
7x = 168
x = 24
Therefore,
The classroom had 24 glue bottles.
Learn more about expressions here:
https://brainly.com/question/3118662
#SPJ1
1. The volume of a 3-D shape is 27 cubic inches. The shape is scaled up by a factor of 3. What is the
volume of the new shape?
Answers
Answer:
81
Step-by-step explanation:
27 * 3 = 81
-5 ≤ -2; Add 7 to both sides
Help pls
Answers
Answer:
2 ≤ 5
Step-by-step explanation:
-5 ≤ -2 add 7 to both sides
-5+7 ≤ -2+7 calculate
2 ≤ 5
Solve for x.
3x - 9 + 4x = 12
A
x = 21
B
x = 3/7
C
x = 3
D
x = -21
Answers
Answer:
x = 3
Step-by-step explanation:
Add 9 to both sides of the equation:
3x - 9 + 4x = 12
3x - 9 + 4x + 9 = 12 + 9
3x + 4x = 21
7x = 21
Divide both sides by 7:
7x ÷ 7 = 21 ÷ 7
x = 3
Hope this helps!
Group like terms: 3x - 9 + 4x = 12
Add similar elements: 3x + 4x = 7x
7x - 9 = 12
Add 9 to both sides: 7x - 9 + 9 = 12 + 9
Simplify: 7x = 21
Divide both sides by 7: 7x/7 = 21/7
Simplify: x = 3
The answer is C) x = 3