geometry, i have other questions ill post in a minute but i need the answers aaa

Answers
Answer:
Angle 6 = 91 degrees
Step-by-step explanation:
There are several ways you could use to find angle 6.
You could either find angle 5 then 6, 2, then 6, or 4 then 6 as they can all be found using the given angle with different rules.
First, we can find angle 5 using the corresponding angles rule which states that angles in the same corresponding quadrant are equal. That is angles that are in the same corresponding 'section' in their groups of angles at both intersect points. E.g. Angle 5 and 89 are corresponding angles, therefore angle 5 is equal to 89.
From here we can find angle 6 by using the rule that states that angles on a straight line add to 180. Angle 6 and angle 5 make up a straight line together which we know is 180 degrees. Therefore 180 - angle 5 = angle 6
180 - 89 = 91
Angle 6 is 91 degrees.
We also could have done this by first finding angle 2, which in on a straight line with the given angle. Therefore 180 - 189 = angle 2
Angle 2 = 91
Then used the corresponding angle rule to find angle 6. Angle 2 = Angle 6
Angle 6 = 91.
The final way we could have found it is by finding angle 4 first. The opposite angles rule states that opposite angles sharing a vertex are equal. This means that 89 and Angle 4 are equal. From there we can use the co-interior rule which states that angles in the same 'section' between parallel lines are co-interior (Angle 4 and angle 6) and are equal.
Therefore angle 4 = angle 6
Angle 6 = 91
Sorry if this answer was a bit confusing, hope it helps!
Related Questions
Helen went to the grocery store to buy potatoes. The store charges $1.13 for each pound of potatoes. On the way out of the store, Helen picked up a gallon of ice cream at a cost of $4.41. If Helen spent $11.19 at the store, how many pounds of potatoes did she purchase? Assume tax is included in the given price.
A. 7
B. 6
C. 8
D. 11
Answers
11.19 - 4.41 = 6.78
James wants to tile his floor using tiles in the shape of a trapezoid. To make the pattern a little more interesting he has decided to cut the tiles in half along the median. The top base of each tile is 12 inches in length and the bottom base is 16 inches. How long of a cut will John need to make so that he cuts the tiles along the median? O A. 2 inches B. 4 inches O C. 14 inches O D. 28 inches
Answers
Answer:
Choice C. 14 inches
Step-by-step explanation:
Middle between 12 and 16 inches.
12. Find the value of x.
(10x - 11)
(7x + 4)

Answers
Answer:
Step-by-step explanation:
7x+4=10x-11
4=3x-11
15=3x
x=5
Think About the Process The length of a rectangle is twice the width. The area of the rectangle is 9
square units. Notice that you can divide the rectangle into two squares with equal area. How can you
estimate the side length of each square? Estimate the length and width of the rectangle.
Answers
Answer:
The side length of each square is 2.12 units.
The length ad width of the rectangle are 2.12 and 4.24 units
Step-by-step explanation:
Let the width of the rectangle is x,
So, the length of the rectangle is 2x.
Area of the rectangle = 9 sq. units
\(9 = 2x \times x\) [as area = length x width]
\(\Rightarrow 9 = 2x^2\)
\(\Rightarrow x^2 = \frac{9}{2}=4.5\)
\(\Rightarrow x = 1.5\sqrt{2}=2.12\) units
So, width of the rectangle, x= 2.12 units and
the llengthof the rectangle, 2x= 2 x 2.12= 4.24 units.
After division of the rectangle into two equal square, so, the area of each square will be half of the area of the rectangle.
The area of the rectangle = 9/2=4.5 square units.
Let a be the length of the sides of the square, so
Area \(= a^2\)
\(\Rightarrow a^2=4.5\)
\(\Rightarrow\) \(a = 1.5\sqrt{2}=2.121\)
Hence, the side length of each square = 2.12 units.
Select all the statements about the number 2-^3 that are true. 2-^3 is equal to -8
Answers
The true statement about the number 2^(-3) is that it is equal to 0.125, not -8
I'm sorry, but the statement "2-^3 is equal to -8" is not true. The correct calculation for 2 raised to the power of -3 is as follows:
2^(-3) = 1 / (2^3) = 1 / 8 = 0.125
The exponent of -3 signifies that we are calculating the reciprocal or inverse of the base number raised to the power of 3. In this case, the base number is 2, and raising it to the power of -3 results in the reciprocal, which is 1/8 or 0.125.
It's important to note that negative exponents indicate the use of fractions or decimals in the calculations. In this context, the negative exponent signifies the inverse or reciprocal of the base number raised to a positive exponent.
Therefore, the true statement about the number 2^(-3) is that it is equal to 0.125, not -8.
It's crucial to understand the concept of exponentiation and the rules associated with it. Negative exponents have specific meanings and should be handled correctly to avoid mathematical errors or misunderstandings.
Learn more about statement here
https://brainly.com/question/2263644
#SPJ11
Alfred delivers 10 to the power of 2 newspapers every week. How many does he deliver in 14 weeks?
Answers
Answer:
1400
Step-by-step explanation:
10² is 100 so 100*14 is 1400
a number is multiplied by 7 then 2.5 is added the result is 58.5
Answers
Answer:
The number is 8
Step-by-step explanation:
You subtract 2.5 from 58.5 which would be 56 and divided that by 7 which would give you he number 8.
what is the equation of the line that is perpendicular to y = −2x + 5 through the point (-4, -5)
Answers
Step-by-step explanation:
m1=-2
m1m2=-1
-2m2=-1
m2=1/2
y+5/x+4=1/2
so 2y+10=x+4
2y-x=-6
Answer:
\(y=\frac{1}{2}x-3\)
Step-by-step explanation:
Hi there!
We are given the equation y=-2x+5 and we want to find the equation of the line that is perpendicular to that line, and pass through the point (-4, -5)
Perpendicular lines have slopes that multiply to get -1.
So to find the slope of the perpendicular line: use the formula \(m_1*m_2=-1\), where \(m_1=-2\)
Substitute:
-2m=-1
Divide both sides by -2
m=\(\frac{1}{2}\)
Here's the equation of the line so far, as we know it, written in slope-intercept form (y=mx+b, where m is the slope and b is the y intercept):
\(y=\frac{1}{2}x+b\)
We need to find b.
Because we know the line passes through the point (-4, -5), we can use it to help solve for b.
Substitute -4 as x and -5 as y
\(-5=\frac{1}{2}(-4)+b\)
Multiply:
-5=-2+b
Add 2 to both sides
-3=b
Substitute -3 as b:
y=\(\frac{1}{2}x-3\)
Hope this helps!
1/2(3x-2/3)+6 less or equal to x+5
Answers
The inequality which represents the given phrase is 1/2(3x - 2/3) + 6 ≤ x+5 and the solution are x ≤ -4/3.
What is inequality?A difference between two values indicates whether one is smaller, larger, or basically not similar to the other.
In other words, inequality is just the opposite of equality for example 2 =2 then it is equal but if I say 3 =6 then it is wrong the correct expression is 3 < 6.
As per the given,
1/2(3x - 2/3) + 6 ≤ x+5
3/2 x - 1/3 + 6 ≤ x+5
3/2 x + 17/3 - x ≤ 5
x/2 ≤ -2/3
x ≤ -4/3
Hence "The inequality 1/2(3x - 2/3) + 6 ≤ x+5 represents the provided sentence, and the answer is x ≤ -4/3.".
For more about inequality,
brainly.com/question/20383699
#SPJ1
A kiddie pool holds miniature plastic ducks in different colors. Sophia randomly picks up a duck and then replaces it. She repeats this process 100 times. The table shows the results of her experiment.
Duck Color Times Picked
red 30
green 20
yellow 40
blue 10
What is the relative frequency of choosing a red duck? What color of duck is there likely to be the most of in the pool?
A.
The relative frequency is 0.3. It is likely that most ducks are blue.
B.
The relative frequency is 0.2. It is likely that most ducks are yellow.
C.
The relative frequency is 0.3. It is likely that most ducks are yellow.
D.
The relative frequency is 0.2. It is likely that most ducks are green.
Answers
Answer:
.3 and most ducks are yellow - so letter c.
Step-by-step explanation:
remember: the formula for relative frequency is f/n.
f = number of times data occurred for an observation (30 red ducks picked)
n - total frequencies (100 ducks picked in total)
30/100 = 0.3 is the relative frequency of choosing a red duck.
Next,
Yellow was picked 40 out of the 100 times, so its likely that most ducks are yellow.
Answer:
C. The relative frequency is 0.3. It is likely that most ducks are yellow.
Step-by-step explanation:
Relative frequency (or experimental probability) is calculated by dividing the recorded number of times an event happens by the total number of trials in the actual experiment.
\(\begin{aligned}\implies \sf Relative\:frequency\:(red\:duck) & = \dfrac{\textsf{Number of times a red duck was picked}}{\textsf{Total number of trials}}\\\\ & = \sf \dfrac{30}{100}\\\\ & = \sf 0.3\end{aligned}\)
The most likely color of duck in the pool is the color of duck with the highest frequency. Therefore, it is likely that most ducks are yellow.
Calculate the distance between the points A=(-1, 3) and K=(2, -3) in the coordinate plane.
Round your answer to the nearest hundredth.
Answers
Answer:
7
Step-by-step explanation:
6.70820393 rounded is 7
Question from the lawyer: "Dr. Expert, I only see a 70° angle here, Exhibit A. Kelly said that having this angle means you have a plane. From what I see, none of the definition of a plane say that an angle defines a plane. Explain how each definition proves that an angle defines a plane."
14. Definition 1: Three points that are not collinear.
Proof:
15. Definition 2: A line and a point not lying on the line.
Proof:
16. Definition 3: Two lines which intersect
Proof:
I need help with the proof :)
Answers
Answer:
14. Three points tat are not collinear
Three points that are not colinear consist of a line and a third point, therefore, joining all three points form a flat figure having a length and a width which is a two-dimensional flat figure or a plane
15. A line and a point not lying on the line
Like the example above, the joining of the points results in a two dimensional figure having a length and a width also known as a planar surface
16. Two lines which intersect at a point
Given two lines that intersect at a point, joining the other end point of the two lines results in the forming of a flat figure, that can be described in two dimensions also known as a planar surface or plane
Step-by-step explanation:
A plane in mathematics is a flat surface that has only two dimensions and extends infinitely in all directions
Find the perimeter of the following figure.
x + 13
3x + 2
8
2
X + 5
Answers
Answer:
5x+30
Step-by-step explanation:
simply add each side together:
(x+13)+(3x+2)+8+2+(x+5)
=5x+30
I need help with this question

Answers
The length of the legs of the right triangle are 2.83 units.
How to find the side of a right triangle?A right tangle triangle is a triangle that has one of its angles as 90 degrees. The sum of angles in a triangle is 180 degrees.
Therefore, the legs of the triangle can be found using trigonometric ratios.
Hence,
sin 45 = opposite / hypotenuse
sin 45 = a / 4
cross multiply
a = 4 × 0.70710678118
a = 2.83 units
Therefore,
cos 45 = b / 4
cross multiply
b = 0.70710678118 × 4
b = 2.82842712475
b = 2.83 units
Therefore, the legs are 2,83 units
learn more on right triangle here: https://brainly.com/question/29285631
#SPJ1
Help please 1. Solve the system of equations using substitution. Show your work in the workspace provided below.
y= 6x +1
y=-2 +6x
2. Solve the system of equations using substitution. Show your work in the workspace provided below
2x-3y=-1
Y=x-1
Answers
Answer:
x=4 y=3
its the answer for both
hope that helps
2( z + 1 ) - 4(z - 4) ≤ 2(z + 5)
please help
Answers
Answer:
z>=2
Step-by-step explanation:
2z+2-4z+16<=2z+10
8<=4z
z>=2
Answer:
z\(\geq\)2
Step-by-step explanation:
2( z + 1 ) - 4(z - 4) ≤ 2(z + 5)
2z + 2 - 4z + 16 \(\leq\) 2z + 10
2 - 4z+ 16 \(\leq\) 10
18 - 4z \(\leq\) 10
-4z \(\leq\) 10 - 18
\(\frac{-4z}{-4\\}\) \(\leq\) \(\frac{-8}{-4}\)
z \(\geq\) 2
What is the Integral Calculator with Steps for
Answers
An integral calculator with steps is a tool that allows you to compute integrals of functions and provides a step-by-step solution to the problem.
This type of calculator is especially useful for students learning calculus, as it allows them to see how the integral is computed and helps them to understand the underlying concepts and techniques.
To use an integral calculator with steps, you typically enter the function you want to integrate and the limits of integration. The calculator then applies a variety of techniques to compute the integral, such as substitution, integration by parts, partial fractions, or trigonometric substitutions.
The output of the calculator usually includes the solution to the integral, as well as a detailed explanation of the steps involved in the computation. Some calculators may also provide graphs of the function and the area under the curve.
Learn more about calculus :
https://brainly.com/question/6581270
#SPJ4
the value of a boat is 21 200. it loses 6 of its value every year. find the approximate monthly percent decrease in value.
Answers
The approximate monthly percent decrease in value of the boat is 0.5%.
The given value of a boat is 21 200, and it loses 6% of its value every year. We are to find the approximate monthly percent decrease in value.
The given information is as follows: The value of a boat = $21,200The percentage decrease in value = 6%We are to find the approximate monthly percent decrease in value. Annual decrease in value of a boat is 6% of $21,200= $1,272Monthly decrease in value of a boat will be 1/12 of the annual decrease = $1,272/12≈ $106Thus, the approximate monthly percent decrease in value of the boat will be
\($\frac{106}{21,200}*100\%=0.5\%$\)
Therefore, the approximate monthly percent decrease in value of the boat is 0.5%.
Learn more about percentages and exponential decay:https://brainly.com/question/29634879
#SPJ11
Your question is incomplete, but probably the complete question is :
The value of a boat is $21,200. It loses 6% of its value every year. Find the approximate monthly percent decrease in value. Round your answer to the nearest hundredth of a percent.
The number of responses to a survey are shown in the Pareto chart. The survey asked 1052 adults how they would grade the quality of their public schools. Each person gave one response,
Find each probability
(a) Randomly selecting a person from the sample who did not give the public schools an A
(1) Randomly selecting a person from the sample who gave the public schools a grade better than a D
(c) Randomly selecting a person from the sample who gave the public schools a Dor an F
(d) Randomly selecting a person from the sample who gave the public schools an A or B
(a) The probability that a randomly selected person did not give the public schools an Als
(Round to three decimal places as needed)
Answers
Answer: (a) P(no A) = 0.935
(b) P(A and B and C) = 0.0005
(c) P(D or F) = 0.379
(d) P(A or B) = 0.31
Step-by-step explanation: Pareto Chart demonstrates a relationship between two quantities, in a way that a relative change in one results in a change in the other.
The Pareto chart below shows the number of people and which category they qualified each public school.
(a) The probability of a person not giving an A is the difference between total probability (1) and probability of giving an A:
P(no A) = \(1-\frac{68}{1052}\)
P(no A) = 1 - 0.065
P(no A) = 0.935
b) Probability of a grade better than D, is the product of the probabilities of an A, an B and an C:
P(A and B and C) = \((\frac{68}{1052})(\frac{258}{1052})(\frac{327}{1052})\)
P(A and B and C) = \(\frac{5736888}{1164252608}\)
P(A and B and C) = 0.0005
c) Probability of an D or an F is the sum of probabilities of an D and of an F:
P(D or F) = \(\frac{269}{1052} +\frac{130}{1052}\)
P(D or F) = \(\frac{399}{1052}\)
P(D or F) = 0.379
d) Probability of an A or B is also the sum of probabilities of an A and of an B:
P(A or B) = \(\frac{68}{1052} +\frac{258}{1052}\)
P(A or B) = \(\frac{326}{1052}\)
P(A or B) = 0.31

The patient's recovery time from a particular surgical procedure is normally distributed with a mean of 7 days and a standard deviation of 7.92 days. What is the probability that it will take more than 11 day to a randomly selected patient to recover from the surgical procedure? QUestion 7 The patient's recovery time from a particular surgical procedure is normally distributed with a mean of 20 days and a standard deviation of 2.24 days. Let X - is the number of days a randomly selected patient needs to recover from the surgical procedure. What is the upper bound of the 90% confidence interval of X ? QUESTION 8 The time needed to find a parking space is normally distributed with a mean of 15 minutes and a standard deviation of 4.89 minutes. 90% of the time, it takes more than how many minutes to find a parking space?
Answers
The upper bound of the 90% confidence interval for the recovery time is approximately 23.696 days.
It takes more than approximately 21.257 minutes to find a parking space 90% of the time.
To find the probability that it will take more than 11 days to recover from the surgical procedure, we need to calculate the area under the normal distribution curve to the right of 11 days.
Mean (μ) = 7 days
Standard deviation (σ) = 7.92 days
We can standardize the value of 11 days using the z-score formula:
z = (x - μ) / σ
z = (11 - 7) / 7.92
z = 0.506
Using a standard normal distribution table or a calculator, we can find the probability corresponding to the z-score of 0.506. The probability is approximately 0.3051.
Therefore, the probability that it will take more than 11 days to recover is approximately 0.3051 or 30.51%.
Question 8:
To find the upper bound of the 90% confidence interval for the number of days needed to recover from the surgical procedure, we need to calculate the z-score corresponding to the desired confidence level and then find the corresponding value using the standard deviation.
Given:
Mean (μ) = 20 days
Standard deviation (σ) = 2.24 days
For a 90% confidence interval, the z-score corresponding to the upper tail probability of 0.10 (1 - 0.90) is approximately 1.645.
Using the formula for the upper bound of the confidence interval:
Upper bound = μ + (z * σ)
Upper bound = 20 + (1.645 * 2.24)
Upper bound ≈ 23.696
Therefore, the upper bound of the 90% confidence interval for the recovery time is approximately 23.696 days.
Question 9:
To find the time it takes more than 90% of the time to find a parking space, we need to calculate the z-score corresponding to the desired upper tail probability and then find the corresponding value using the standard deviation.
Mean (μ) = 15 minutes
Standard deviation (σ) = 4.89 minutes
For a probability of 90%, the upper tail probability is 1 - 0.90 = 0.10.
Using a standard normal distribution table or a calculator, we can find the z-score corresponding to the upper tail probability of 0.10, which is approximately 1.282.
Using the formula for the upper bound:
Upper bound = μ + (z * σ)
Upper bound = 15 + (1.282 * 4.89)
Upper bound ≈ 21.257
Therefore, it takes more than approximately 21.257 minutes to find a parking space 90% of the time.
Learn more about approximately from
https://brainly.com/question/27894163
#SPJ11
Anthony and Jesus decide that they want to buy a Playstation 5 together. They each have $225. Ray has a Gamestop coupon that gives him 10% off his order, so they decide to go to Gamestop. The price of the Playstation is $499.00. If tax is 7%, will they be able to buy the console? If not, how much money will they have to borrow from their parents?
Answers
Answer:
Yes, they will have enough.
Step-by-step explanation:
1. $499.00 + 7% = $533.93
2. $225 x 2 = $550
3. $550 - $533.93 = $16.07 left to spend
Is the rate of change of the function 5?

Answers
Answer:
No because the x value does not change by 1 everytime the y value changes by 5
Step-by-step explanation:
Rate of Change = Slope
If the slope was 5, the the point on the graph would be on the coordinate (1,5)
However, the graph provided does NOT show 5 as being the slope because the line does not go through 0 and the x value does not change by 1 everytime y changes by 5.
If it did, however, it would look something like this picture.

Answer:^^^ that Guy is so wrong but the actual answer is b
Step-by-step explanation:
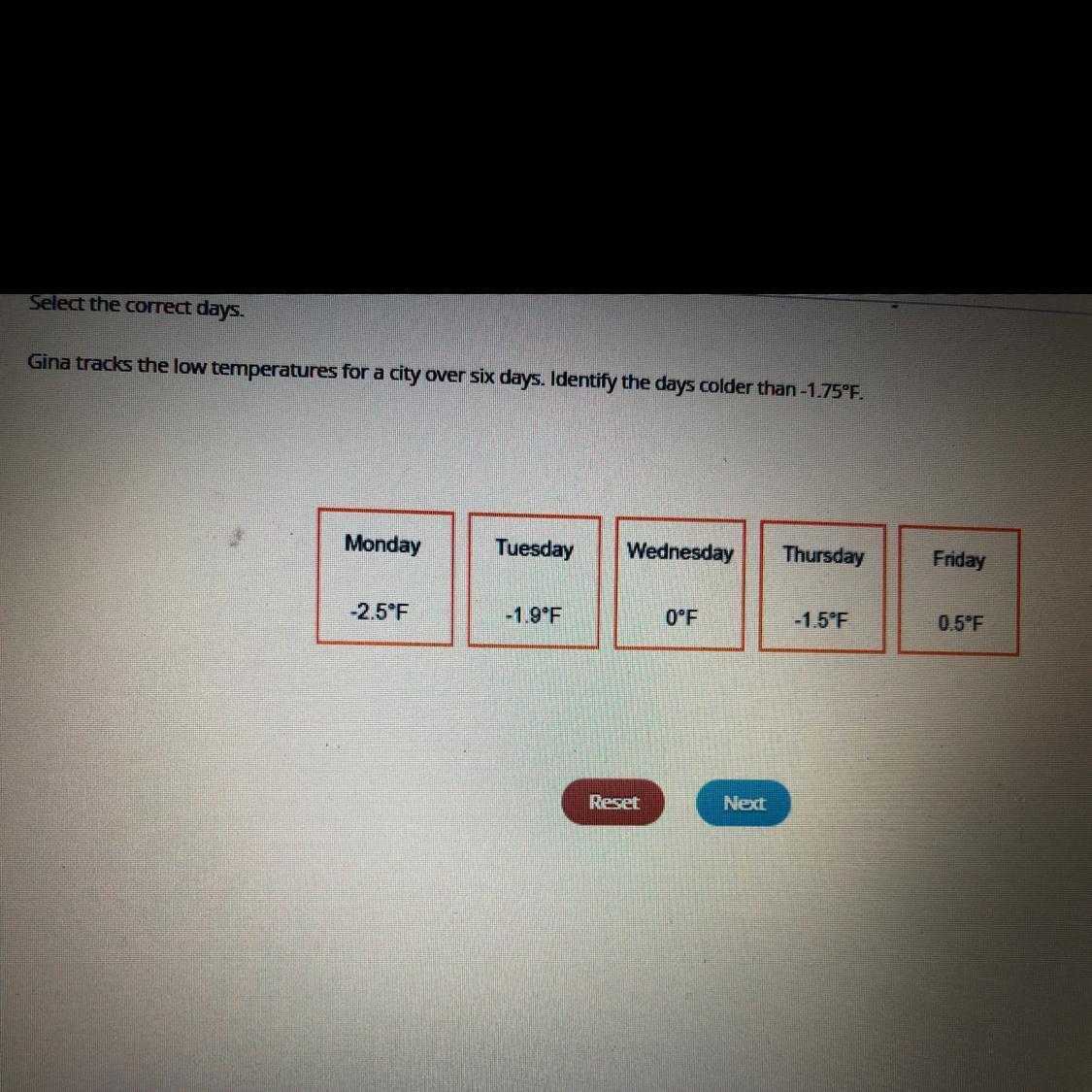
Select the correct days. Gina tracks the low temperatures for a city over six days. Identify the days colder than -1.75°F.
Answers
Answer:
\(Monday = -2.5F\)
\(Tuesday = -1.9F\)
Step-by-step explanation:
Given
See attachment
Required
Days colder than -1.75°F
From the attachment, we have:
\(Monday = -2.5F\)
\(Tuesday = -1.9F\)
\(Wednesday = 0F\)
\(Thursday = -1.5F\)
\(Friday = 0.5F\)
Days with temperature less than -1.75°F are colder.
-2.5 and -1.9 are less than -1.75
So, we have:
\(Monday = -2.5F\)
\(Tuesday = -1.9F\)
Answer:
:)
Step-by-step explanation:
PLS HELP!!! FIRST GETS BRAINLIEST!
Which ordered pairs make both inequalities true? Check all that apply.
(−5, 5)
(0, 3)
(0, −2)
(1, 1)
(3, −4)

Answers
Answer:
(0,-2) and (1,1)
Step-by-step explanation:
The solution points at the intersection of what is above the orange line and belothe blue line.
(-5, 5) is only in the orange zone so X
(0,3) is on the blue line that is doted so X
(0,-2) is on the orange line that is solid so ✅
(1,1) is in the orange and blue so ✅
(3,-4) is in the blue zone only so X
Answer:
hoi
Step-by-step explanation:
What is the mole of H2?
Answers
One mole of H2 contains 6.022 x 10^23 H2 molecules. This can be used to calculate the number of H2 molecules in a given volume or mass of hydrogen gas.
What is mole?A mole is a unit of measurement in chemistry that expresses the amount of a substance. It is defined as the number of entities (such as atoms, ions, or molecules) in a sample of the substance. The number of entities in one mole of a substance is known as Avogadro's number.
What is Avogadro's number?Avogadro's number is a fundamental constant of physics and chemistry, defined as the number of atoms, ions or molecules in one mole of substance. It is approximately 6.022 x 10^23 and is used in many calculations in chemistry and physics, such as the number of atoms in a sample of an element, the number of ions in a salt, or the number of molecules in a gas sample. The constant is named after Amedeo Avogadro, an Italian scientist who first proposed the concept in 1811.
One mole of a substance is equal to Avogadro's number, which is approximately 6.022 x 10^23.
The mole of H2 (hydrogen gas) is the number of H2 molecules in a sample of hydrogen gas. One mole of H2 contains 6.022 x 10^23 H2 molecules. This can be used to calculate the number of H2 molecules in a given volume or mass of hydrogen gas.
To know more about mole visit:
https://brainly.com/question/26416088
#SPJ4
There are 10 card each giving a diffrent number from 1 to 10 uppoe elect one card from the tack what i the odd and econd i greater the 8 what i porblity that the econd number i greater the 8
Answers
Using the Probability formula ,
the probability that first card is odd and second card is greater than 8 is 1/10.
Probability is defined as the total number of favourable outcomes divided by total numbers of outcomes.
We have total 10 cards between 1 to 10 there are 5 even and 5 odd numbers.
so, Total possible outcomes = 10
= {1,2,3,4,5,6,7,8,9,10}
two different cards are drawn out of 10 cards favourble outcomes ( odd card drawn on first draw) = 5
probability that first card is odd(P₁) = 5/10
numbers greater than 8 = {9,10 } = 2
probability that second card is greater than 8 (P₂)
= 2/10
Now , probability that first card is odd and second one is greater than 8 = P₁×P₂ = (5/10)×(2/10) = 1/10
Hence, total probability that first card is odd and second one is greater than 8 is 1/10 .
To learn more about Probability, refer:
https://brainly.com/question/25688842
#SPJ4
The water fountain produces 32 liters of water in 4 minutes. if this represents a proportional relationship, what is the unit rate of how many liters are produced in 1 minute?
Answers
Answer:
8 liters for 1 minute
Step-by-step explanation:
Divide 32 by 4 = 8
And so the unit rate 8/1
1.
Identify the vertex and the y-intercept of the graph of the function.
y = 0.5(x – 3)^2
A. vertex, (3, 0); y-intercept 4.5
B. vertex, (–3, 0); y-intercept, 4.5
C. vertex, (–3, 0); y-intercept, 1.5
D. vertex, (3, 0); y-intercept, 1.5
Answers
Answer:
A. vertex, (3, 0); y-intercept 4.5
Step-by-step explanation:
Rewrite in vertex form and use this form to find the vertex
( h , k ) . ( 3 , 0 )
To find the x-intercept, substitute in 0 for y and solve for x . To find the y-intercept, substitute in 0 for x and solve for y .
x-intercept(s):
( 3 , 0 )
y-intercept(s):
( 0 , 4.5 )


Help please hurry
Maria spins a penny 100 times and it lands head side up 62 times. Explain why Maria's experimental probability may be different from the theoretical probability of spinning a coin. (10 points)
Answers
Answer:
To solve the question we shall proceed as follows:
Theoretical probabilities generally deals with the nature of the experiment and events, this differs from the experimental probabilities relies on the fact of actual occurrence of the experiment and the events. In other words, experimental probability is an estimate simply based on the probabilities that cannot at all be determined by simple logic. It is the ratio of the number of times an event is occurring to the total number of times or trials that an activity has been repeated for.
From the question, the experimental probability will be:
62/100
=0.62
this differs with theoretical probability which states that at any occasion the probability of the coin coming up heads when tossed is 1/2
Step-by-step explanation: I really hope this helps!! :))). Mark me brainliest!! :))
Order these numbers from least to greatest 3.2, 3.017, 3.17, 3.1721 3.2 3.017 3.17 3.1721
Answers
Also, I’m assuming you accidentally typed the numbers in twice as there are two of each number. But either way, it would still be in the same order above :)
Answer:
hey
Step-by-step explanation:
<3