Answers
Answer:
Functions:
3. The chart with arrows
4. The graph
Not Functions:
1. (1,1), (2,2), (3,3), (1,4)
2. (1,17), (0,16), (0,15), (-2,17)
Step-by-step explanation:
Functions do not have repeating domains (x-coordinates).
Hope it helps!
Related Questions
Suppose that X; Y have constant joint density on the triangle with corners at (4; 0), (0; 4), and the origin. a) Find P(X < 3; Y < 3). b) Are X and Y independent
Answers
The triangle (call it T ) has base and height 4, so its area is 1/2*4*4 = 8. Then the joint density function is
\(f_{X,Y}(x,y)=\begin{cases}\frac18&\text{for }(x,y)\in T\\0&\text{otherwise}\end{cases}\)
where T is the set
\(T=\{(x,y)\mid 0\le x\le4\land0\le y\le4-x\}\)
(a) I've attached an image of the integration region.
\(P(X<3,Y<3)=\displaystyle\int_0^1\int_0^3f_{X,Y}(x,y)\,\mathrm dy\,\mathrm dx+\int_1^3\int_0^{4-x}f_{X,Y}(x,y)\,\mathrm dy\,\mathrm dx=\frac12\)
(b) X and Y are independent if the joint distribution is equal to the product of their marginal distributions.
Get the marginal distributions of one random variable by integrating the joint density over all values of the other variable:
\(f_X(x)=\displaystyle\int_{-\infty}^\infty f_{X,Y}(x,y)\,\mathrm dy=\int_0^{4-x}\frac{\mathrm dy}8=\begin{cases}\frac{4-x}8&\text{for }0\le x\le4\\0&\text{otherwise}\end{cases}\)
\(f_Y(y)=\displaystyle\int_{-\infty}^\infty f_{X,Y}(x,y)\,\mathrm dx=\int_0^{4-y}\frac{\mathrm dx}8=\begin{cases}\frac{4-y}8&\text{for }0\le y\le4\\0&\text{otherwise}\end{cases}\)
Clearly, \(f_{X,Y}(x,y)\neq f_X(x)f_Y(y)\), so they are not independent.

()
Complete the table using the given rules. Then, compare pattern A to pattern B.
() Pattern A
◄) subtract 20
Pattern B
() subtract 4
100
20
Which statement is true?
Each term in pattern B is 80 less than the corresponding term in pattern A.
Each term in pattern B can be found by dividing the corresponding term in
pattern A by 5.

Answers
Answer:
100; 80, 60, 4020; 16, 12, 8dividing by 5Step-by-step explanation:
You want to fill a table using the given rules, then describe the relationship between the table values.
Pattern AStarting with 100, you want to subtract 20 to get next terms:
100
100 -20 = 80
80 -20 = 60
60 -20 = 40
The next terms are 80, 60, 40.
Pattern BStarting with 20, you want to subtract 4 to get next terms:
20
20 -4 = 16
16 -4 = 12
12 -4 = 8
The next terms are 16, 12, 8.
RelationshipLooking at second terms, we can determine which description is true:
80 -80 = 0 ≠ 16 . . . . . the description "subtract 80" fails
80/5 = 16 . . . . . . . . . . the description "divide by 5" works
Each term in pattern B can be found by dividing the corresponding term in pattern A by 5.
Lisa and Susan are driving to college together. They look at a map to find out how far they have to drive. On the map, Lisa measures the distance to be 4.5 inches. How many miles do they have to drive if the map scale is 1 in. = 35 mi?
Answers
Answer:157.5
Step-by-step explanation:becuase mutilpy 4.5x35 that equals 157.5
Write the equation of the question.

Answers
The equation of the line with slope 1/3 and y-intercept as -1 is y = x/3-1 in slope-intercept form.
According to the question,
We have the following information:
Slope of the line = 1/3
We know that the slope of the line is denoted by m.
y-intercept of the line = -1
We know that the y-intercept is denoted by b.
We have the following equation for the line in slope-intercept form:
y = mx+b
Putting the above values in this equation:
y = x/3-1
Hence, the equation of the line with slope 1/3 and y-intercept as -1 is y = x/3-1 in slope-intercept form.
To know more about equation of the line here
https://brainly.com/question/402319
#SPJ1
-8-8-6-2 4 12 22
What is the nth term rule of the quadratic sequence
Answers
Answer:
\(n^2 -3n - 6\)
Step-by-step explanation:
Looking at the image attached, you must first work out the difference between each term. This is +0, +2, +4, +6, +8, +10 (shown in orange).
Because you now have a linear sequence, the difference is now the same each time. This is +2 (shown in blue).
Because the original sequence is a quadratic, you have to halve the second difference (the +2). This means that the value of \(n^2\) is 1, so 1\(n^2\) or just \(n^2\) .
If you write out the values of \(n^2\), you can work out how much more you need to add or take away. For example, take the first three terms in the sequence.
n = 1, 2, 3
x = -8, -8, -6
\(n^2\) = 1, 4, 9
Work out the difference between \(n^2\) and x:
1 - -8 = 9
4 - -8 = 12
9 - -6 = 15
This gives you yet another linear sequence, 9, 12, 15.
Working out the formula for this, the difference is 3 each time, so it is 3n. The first value of n is 1, so 3n is 1. The difference is 6, so the formula for this linear sequence is 3n + 6.
Because \(n^2\) is greater than x, you need to take 3n + 6 away from \(n^2\).
This gives \(n^2\) - (3n+6), so the final answer is:
\(n^2\) - 3n - 6.

44% of the group were rested. The group numbered 76. How many were rested?
Answers
Rested numbers in group is 33 out of 76.
What is a percentage?A percentage is expressed as a number or ratio that can be expressed as fraction of 100. It is denoted by % symbol.
Total numbers in a group = 76.
44% of them were rested.
That is 44% of 76.
To find how many are rested we have to find the value in numbers.
Convert 44% of 76 to numbers.
For this, it can be written as
\(\frac{44}{100} *76\) = 33.44
Therefore 44% of 76 ≅ 33 numbers.(approximately)
Hence, rested numbers in group is 33.
Learn more about percentage here:
https://brainly.com/question/16797504
#SPJ1
Gracy has fraction 4 over 5 pound of bird seed. She needs fraction 3 over 10 pound to feed the birds daily. Which of the rectangle models below shows how many days’ worth of seed Gracy has left?
Answers
Answer:
The last one is correct.
Step-by-step explanation:
[] Rewrite 4/5 as 8/10
[] 8/10 / 3/10 = 8/10 * 10/3 = 80/30 = 2 2/3 days
Have a nice day! - This is only correct if your models look like the ones I have attached
I hope this is what you are looking for, but if not - comment! I will edit and update my answer accordingly. (ノ^∇^)
- Heather

Problem’s in the image

Answers
The growth rate function indicates that the number of years The Iron Man's net worth will reach the net worth of T'Challa is about 87 years
What is a growth rate?The growth rate is the rate of growth of a function with regards to the input variable.
T'Challa's net worth in the Marvel comics = 80 trillion (8 × 10¹³) Dollars
The Iron Man's net worth = 20 billion (2 × 10¹⁰) Dollars
The growth rate per annum of The Iron Man's net worth = 10% per annum
The number of years it will take to reach T'Challa can therefore, be found as follows;;
(2 × 10¹⁰) × (1 + 0.1)ˣ = (8 × 10¹³)
(1 + 0.1)ˣ = (8 × 10¹³)/(2 × 10¹⁰)
x·ln(1 + 0.1) = ln((8 × 10¹³)/(2 × 10¹⁰))
x = (ln((8 × 10¹³)/(2 × 10¹⁰)))/(ln(1 + 0.1)) ≈ 87 years
Learn more on the growth rate function here: https://brainly.com/question/29334875
#SPJ1
please simplify answer i need the correct answer

Answers
The volume of the sphere is 32 cubic feet.
To calculate the volume of sphere, apply the formula given below;
The formula for the volume of a sphere can be described as:
V = (4/3)πr³
where r is the representation of the radius of the sphere.
Given that the radius of the sphere is 2 feet and π = 3, we can substitute these values into the formula to get:
V = (4/3)π(2³)
= (4/3)π(8)
As per the given information π = 3,
V = (4/3)(3)(8)
V = 32 cubic feet.
Therefore, the required volume is 32 cubic feet.
To learn more about the volume of a sphere;
https://brainly.com/question/9994313
#SPJ1
solve the quadratic equation by using the quadratic formula. if the solution are not real, enter N/A 3x^2-7x+1=0
Enter the exact answer.
Answers
Answer:
\(\displaystyle x=\frac{7\pm\sqrt{37}}{6}\)
Step-by-step explanation:
\(\displaystyle x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\\\\x=\frac{-(-7)\pm\sqrt{(-7)^2-4(3)(1)}}{2(3)}\\\\x=\frac{7\pm\sqrt{49-12}}{6}\\ \\x=\frac{7\pm\sqrt{37}}{6}\)
(45 points)
7. Find the length of YU Round to the nearest hundredth.
8. Find STR.

Answers
Answer:
YU = 4.82. angle STR = 23°
Step-by-step explanation:
7) Angle between U and V = 72°, since angles on a straight line add up to 180°. so angle UV = 180 - 108 = 72°.
similarly, angle YU = 180 - 85 - 72 = 23°.
length of circumference of full circle = π X diameter = π (2r)
= 2πr (radius = half of diameter).
circumference = 2π(12) = 24π.
there are 360° in full circle.
remember that angle YU = 23°.
length YU = (23/360) X 24π
= (23π)/15
= 4.817
= 4.82 to nearest one hundredth.
8) triangle RST sits inside of half the circle, ie in the semicircle.
angle RST = 90° because the angle in a semicircle = 90°.
there are 180° in a full triangle.
since angle RST = 90°, angle STR must be less than 180 - 90.
angle STR < 90°. so STR must be 23°.
Prove if 5n+3 is odd, then 7n+4 is even
Answers
Use the Leading Coefficient Test to determine the end behavior of the graph of each polynomial function.

Answers
The correct answer is a. -∞, f(x) → -∞; x → ∞, f(x) → ∞b. -∞, f(x) → -∞; x → ∞, f(x) → ∞c. -∞, f(x) → -∞; x → ∞, f(x) → ∞d. -∞, f(x) → -∞; x → ∞, f(x) → -∞
For the polynomial function f(x) = 6x^5 + 7x^2 + 7x + 9, the leading coefficient is 6 (the coefficient of the highest-degree term). The degree of the polynomial is 5, which is odd.
According to the Leading Coefficient Test, when the degree of the polynomial is odd and the leading coefficient is positive (in this case, positive 6), the end behavior of the graph is as follows:
- As x approaches negative infinity (-∞), f(x) approaches negative infinity (-∞).
- As x approaches positive infinity (∞), f(x) approaches positive infinity (∞).
For the polynomial function f(x) = 61x^11 + 7x^2 + 2x + 8, the leading coefficient is 61 (the coefficient of the highest-degree term). The degree of the polynomial is 11, which is odd.
Using the Leading Coefficient Test, we can determine the end behavior:
- As x approaches negative infinity (-∞), f(x) approaches negative infinity (-∞) since the leading coefficient is positive.
- As x approaches positive infinity (∞), f(x) also approaches positive infinity (∞) due to the same reason.
For the polynomial function f(x) = 5x^8 + 3x^2 + 2x + 9, the leading coefficient is 5 (the coefficient of the highest-degree term). The degree of the polynomial is 8, which is even.
Applying the Leading Coefficient Test:
- As x approaches negative infinity (-∞), f(x) approaches positive infinity (∞) because the leading coefficient is positive.
- As x approaches positive infinity (∞), f(x) also approaches positive infinity (∞) for the same reason.
For the polynomial function f(x) = -2x^8 + 6x^2 + 4x + 9, the leading coefficient is -2 (the coefficient of the highest-degree term). The degree of the polynomial is 8, which is even.
Using the Leading Coefficient Test:
- As x approaches negative infinity (-∞), f(x) approaches negative infinity (-∞) since the leading coefficient is negative.
- As x approaches positive infinity (∞), f(x) approaches negative infinity (-∞) due to the same reason.
For more such questions on polynomial function
https://brainly.com/question/31528136
#SPJ8
What value of x makes this equation true 5(x-3)=20
Answers
Answer:
X=7
Step-by-step explanation:
5x - 15 =20
5x=15+30
5x=35
Divide by 5
X=7
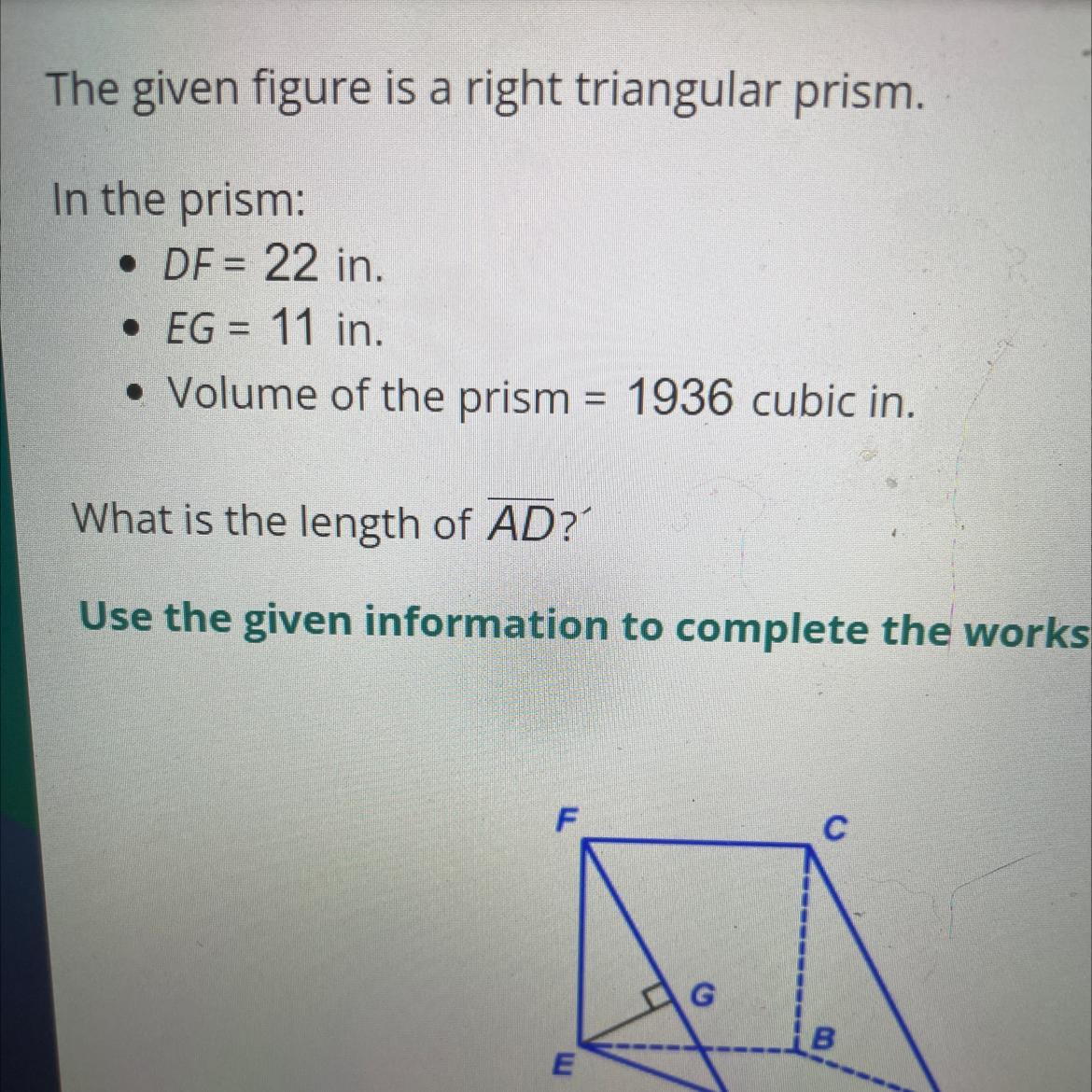
The given figure is a right triangular prism.
In the prism:
• DF = 22 in.
• EG = 11 in.
• Volume of the prism = 1936 cubic in.
What is the length of AD?'
Use the given information to complete the worksheet.
Thank you!
Answers
The length of side AD is,
⇒ AD = 16
We have to given that;
The given figure is a right triangular prism.
In the prism:
• DF = 22 in.
• EG = 11 in.
• Volume of the prism = 1936 cubic in.
Since, Volume of right triangular prism is,
V = 1/2 (bh) x L
Substitute all the values we get;
V = 1/2 (22 × 11) × AD
1936 = 121 × AD
AD = 16
Thus, The length of side AD is, 16
Learn more about the multiplication visit:
https://brainly.com/question/10873737
#SPJ1
eight hundred twenty nine and six tenths as a decimal
Answers
Any other questions ask :)
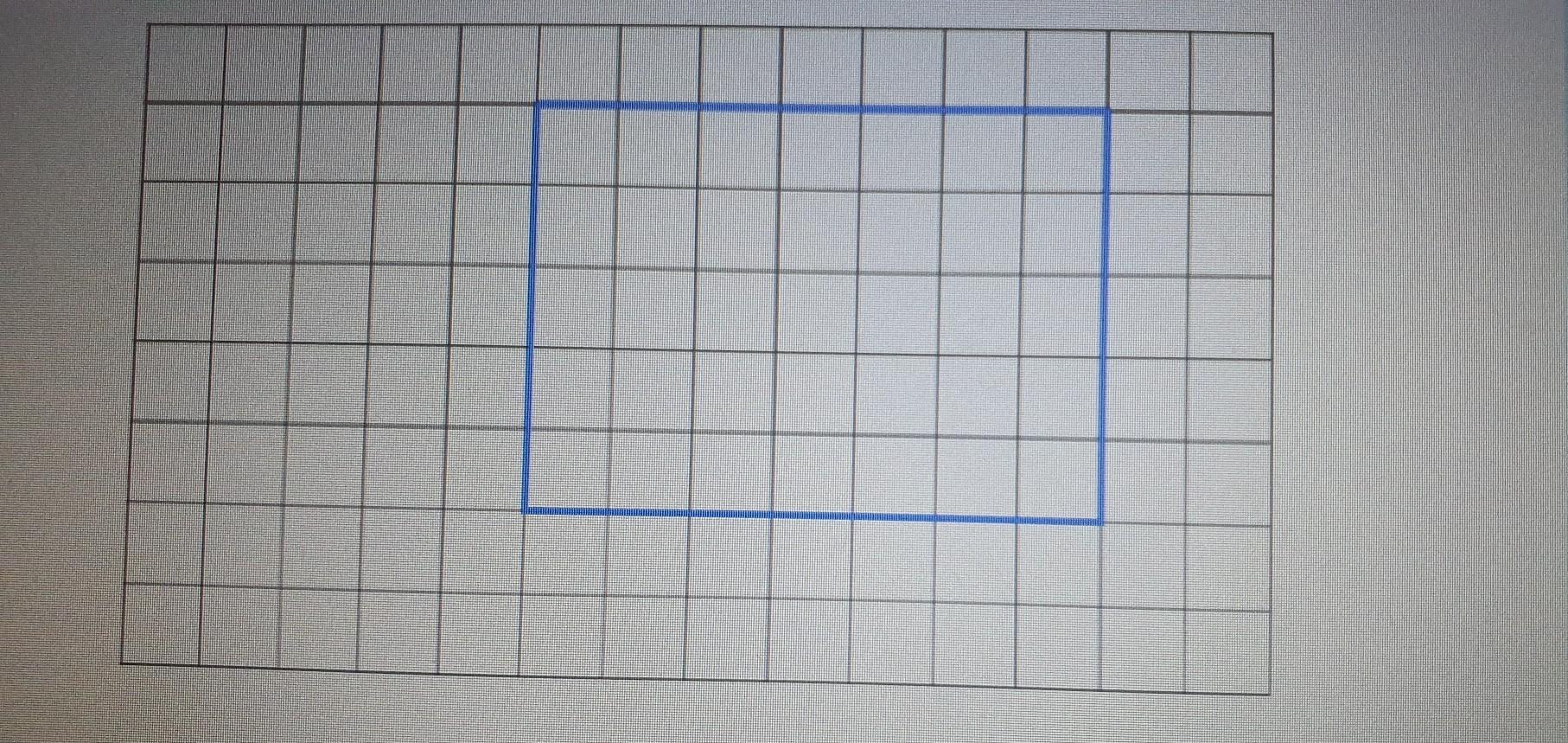
Find the area of the rectangle on this centimetre grid.
Answers
Answer:
A = 35 cm²
Step-by-step explanation:
the area (A) of a rectangle is calculated as
A = length × width
by counting the squares on the sides
length = 7 cm and width = 5 cm , then
A = 7 × 5 = 35 cm²
Find the slope A(5,4) and B(2,10)
Answers
Answer:
Step-by-step explanation:
(10 - 4)/(2 - 5) = -6/3 = -2
Need help with a math question

Answers
First: Find out their decimal form.
- 2 1/6 as a decimal is 2.16
7/3 as a decimal
To get 7/3 converted to decimal, you simply divide 7 by 3. Don't worry. You don't need to get the calculator out, because we did this for you.
7/3 as a decimal is:
2.333333333
A tortoise and a hare are competing in a 2000-meter race. The arrogant hare decides to let the tortoise have a 510-meter head start. When the start gun is fired the hare begins running at a constant speed of 8 meters per second and the tortoise begins crawling at a constant speed of 6 meters per second. -Let t represent the number of seconds that have elapsed since the start gun was fired. 1) Write an expression in terms of t that represents the hare's distance from the starting line (in meters) 2) Write an expression in terms of t that represents the tortoise's distance from the starting line (in meters) 3) Write an expression in terms of t that represents the number of meters the tortoise is ahead of the hare.
Answers
Answer:
1. 8t
2. 510 + 6t
3. 510 - 2t
Step-by-step explanation:
1. Since the hare moves at a speed of 8 metres per second, the distance it moves from the starting line is d = speed × time = 8t
2. Since the rabbit moves at a speed of 6 metres per second, and gets a head start of 510 metres, the distance it moves from the starting line is d = 510 m + speed × time = 510 + 6t
3. The distance the tortoise is ahead of the hare is thus, distance moved by rabbit - distance moved by hare in time, t.
d' = 510 + 6t - 8t
= 510 - 2t
9) The 50 cars used by a firm were inspected. 10 had faulty brakes and 15 had faulty tyres. There were 2 cars with faulty brakes but good tyres. How many cars had good brakes and good tyres? The answer is 33
Answers
Based on the information, there are 25 cars with good brakes and good tires.
How to calculate the valueTotal cars = 50
Cars with faulty brakes = 10
Cars with faulty tires = 15
Cars with faulty brakes and good tires = 2
Let's calculate the number of cars with good brakes and good tires:
Cars with faulty brakes or faulty tires = Cars with faulty brakes + Cars with faulty tires - Cars with faulty brakes and good tires
= 10 + 15 - 2
= 25
Cars with good brakes and good tires = Total cars - Cars with faulty brakes or faulty tires
= 50 - 25
= 25
Therefore, there are 25 cars with good brakes and good tires.
Learn more about numbers on
https://brainly.com/question/25734188
#SPJ1
Find the value of x, 6,4, 3x, 4x+1

Answers
Answer:
If two chords intersect in a circle, then the product of the segments of one chord equals the product of the segments of the other chord.
6(3x) = 4(4x + 1)
18x = 16x + 4
2x = 4
x = 2
(Guys i need an expert verified)
Solve y3 = −216.
A: y = −72
B: y = ±72
C: y = −6
D: y = ±6
Answers
Answer: y = -6.
Step-by-step explanation: -6^3 is -216. Sorry if this isn't a clear explanation, but it seems like the correct choice.
Have a great day! :)
Given A = 31 degree, a = 12 inches, and b = 5 inches, find the remaining side and angles of the triangle
Answers
The remaining angles of the triangle are approximately 72.7 degrees and 76.3 degrees.
What is the law of sine?
A law in trigonometry the ratio of each side of a plane triangle to the sine of the opposite angle is the same for all three sides and angles.
To solve the triangle, we can use the law of sines and the fact that the angles of a triangle add up to 180 degrees.
Using the law of sines, we have:
a/sin(A) = b/sin(B) = c/sin(C)
where c is the unknown side and B and C are the unknown angles.
We can use the given values to solve for sin(A) and plug them into the equation to get:
sin(A) = sin(31) ≈ 0.515
c/sin(C) = 12/0.515
c ≈ 27.89 inches
So the length of the remaining side is approximately 27.89 inches.
To find the angles, we can use the fact that the angles of a triangle add up to 180 degrees. So we have:
B + C = 180 - A
sin(B) = b/c * sin(C)
Substituting the values we know, we get:
B + C = 180 - 31 = 149
sin(B) = 5/27.89 * sin(C)
We can solve the second equation for sin(C) by rearranging to get:
sin(C) = sin(B) * 27.89/5
Then we can substitute into the first equation to get:
B + arcsin(sin(B) * 27.89/5) = 149
We can solve for B using algebra or by using a calculator to evaluate the left side of the equation. Either way, we get:
B ≈ 72.7 degrees
Then we can use the fact that the angles of a triangle add up to 180 degrees to find C:
C = 180 - A - B
= 180 - 31 - 72.7
= 76.3 degrees
hence, the remaining angles of the triangle are approximately 72.7 degrees and 76.3 degrees.
To learn more about the law of sine visit,
https://brainly.com/question/30401249
#SPJ1
William leaves his home at 15:03 and walks for 12 minutes to Euston station.
He spends 4 minutes buying a ticket and then catches the next train to Bletchley.
What time will he arrive at Bletchley?
Train timetable
Euston
14:49 15:18 15:29
14:52
15:32 15:35
Harrow
Watford 15:01
15:30
15:41 15:44 16:11
Hemel
15:39 15:50
15:53
16:20
Tring
15:31
16:00
Q
16:14 16:41
Bletchley 15:47
16:16
16:30
Bedford 15:54 16:23 16:34 16:37 17:04
15:32 15:59
Answers
To find out what time he will arrive at Bletchley, we need to look at the arrival time for the train that departs Euston at 15:32. According to the timetable, this train arrives at Bletchley at 16:16.
William spends 12 minutes walking to Euston station and 4 minutes buying a ticket, so his total journey time is 12 + 4 + 44 = 60 minutes (since there are 60 minutes in an hour). Therefore, he will arrive at Bletchley at 16:16 + 60 minutes = 17:16.
So, William will arrive at Bletchley at 17:16.
*Answer*
15:47
Step-by-step explanation:
He left; 15:03
Walk for; 12mins
Spends extra;4min
So by my side,
I'll sum up those values we're having to find the total time that was spent
12+4= 16mins
So, at that time when he reached at the station it was 15:19 when we add those extra mins
And so I think it'll 15:47
My thought told me so though
103,688- 89,176 equal to what?
Answers
Answer:
The answer is 14512
Step-by-step explanation:
106,688
- 89,176
Find the slope of the line passing through the points (1, -1) and (4, -2).
Answers
Answer:
\(slope=-\frac{1}{3}\)
Step-by-step explanation:
To find the slope of the two points (1, -1) and (4, -2) we have to use the slope formula.
\(slope=\frac{y_{2}- y_{1} }{x_{2} -x_{1} }\) \(slope=\frac{(-2)- (-1)}{4 -1}\)
\(slope=\frac{-1 }{3}=-\frac{1}{3}\) can also be written as a decimal \(slope=-0.333333\)
QUESTION 3: POCKET MONEY Mr Reyan made an agreement with his son Smith who is studying in grade 12 as follows. Smith will get pocket money after he finishes all his homework every day. The amount of pocket money will be double the amount previous day. He will start first day with R1. He can use this saving for his matric dance.
3.1 Write the information as a sequence.what is the sequence of this information?
Answers
The formula for obtaining the value of a term of a sequence is given as a
as a recursive formula.
Responses:
The information as a sequence is; R1, 2·R1, 4·R1, 8·R1, 16·R1, ...The sequence of the information is a geometric sequenceHow is the given information expressed as a sequence?The amount of pocket money Smith gets = 2 × The amount he gets in the previous day
The amount Smith gets on the first day = R1
Required:
The given information expressed as a sequence.
Solution:
The amount of money smith gets can be expressed as follows;
Amount he gets on day 1 = R1
On day 2, R2 = 2·R1
On day 3, R3 = 2·R2 = 2·2·R1 = 4·R1
On day 4, R4 = 2·R3 = 2·2·2·R1 = 8·R1
On day 5, R5 = 2·R4 = 2·2·2·2··R1 = 16·R1
The information written as a sequence is therefore;
R1, 2·R1, 4·R1, 8·R1, 16·R1, ...The type of sequence is a geometric sequence, or progression where the first term is R1, and the common ratio, r = 2Learn more about geometric sequence here:
https://brainly.com/question/4289731
https://brainly.com/question/1532378
I am stumped >:( ahhhhhhh

Answers
Answer:
\(\frac{1}{32} yards^{3}\)
Step-by-step explanation:
\(V=w*h*l\)
↓
\(V= \frac{1}{4} *\frac{1}{4} *\frac{1}{2}\)
=
\(\frac{1}{32} yards^{3}\\\)
Hope this helps!
A small radio transmitter broadcasts in a 56 mile radius. If you drive along a straight line from a city 65 miles north of the transmitter to a second city 68 miles east of the transmitter , during how much of the drive will you pick up a signal from the transmitter ?
Answers
During the entire drive from the first city to the second city, you will be within the signal range of the transmitter.
To determine how much of the drive you will pick up a signal from the transmitter, we need to find the distance between the two cities and compare it to the radius of the transmitter's broadcast.
Using the Pythagorean theorem, we can calculate the distance between the two cities:
Distance = sqrt((65^2) + (68^2))
Distance = sqrt(4225 + 4624)
Distance = sqrt(8849)
Distance ≈ 94.03 miles
Since the distance between the two cities is 94.03 miles and the transmitter's broadcast radius is 56 miles, we can conclude that for the entire duration of the drive, you will be within the broadcast range of the transmitter.
Thus, you will pick up a signal from the transmitter throughout the entire drive.
During the entire drive from the first city to the second city, you will be within the signal range of the transmitter.
For more such questions on transmitter
https://brainly.com/question/29364813
#SPJ8
