Answers
Answer:
Step-by-step explanation:
⅗
Answer:y>-2/3x+3
Step-by-step explanation:
y>-2/3x+3
y is the bigger cause of the dotted lines and not straight lines.
Related Questions
ayuda porfavor
necesito resolver esto es simplificarlo no resolverlo ayuda pls
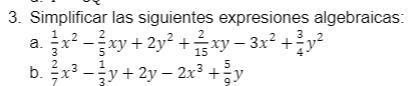
Answers
The Simplification of the algebraic expression gives:
a. -2/3x² - (4/15)xy + (11/4)y²
b. -(12/7)x³ + (20/9)y
How to simplify algebraic expressions?Simplification of an algebraic expression is the process of writing an expression in the most efficient and compact form without affecting the value of the original expression
a. (1/3)x² - (2/5)xy + 2y² + (2/15)xy - 3x² + (3/4)y²
To simplify this, add or subtract like terms. That is:
(1/3)x² - (2/5)xy + 2y² + (2/15)xy - 3x² + (3/4)y²
= (1/3)x² - 3x² - (2/5)xy + (2/15)xy + 2y² + (3/4)y²
= -2/3x² - (4/15)xy + (11/4)y²
b. (2/7)x³ - (1/3)y + 2y - 2x³ + (5/9)y
To simplify this, add or subtract like terms. That is:
(2/7)x³ - (1/3)y + 2y - 2x³ + (5/9)y = (2/7)x³- 2x³ - (1/3)y + 2y + (5/9)y
= -(12/7)x³ + (20/9)y
Learn more about algebraic expression on:
brainly.com/question/4344214
#SPJ1
What is 6 1/4% of 95?
What is 3/10% of 115?
Answers
1.) 95/16
2.) 69/200
Help!
Algebra 2 Honors work D:

Answers

help asap i need this tomorrow thanks!:)

Answers
a) The algebraic fraction \(\frac{{x + 2}}{{(x - 1)^2}}\) is proper. b) The algebraic fraction \(\frac{{4x^2 - 31x + 59}}{{(x - 4)^2}}\) can be expressed as \(-\frac{{31}}{{x - 4}} - \frac{{25}}{{(x - 4)^2}}\).
Let's solve each part step by step and determine whether the fraction is proper or improper, and then express it accordingly.
a) \(\frac{{x + 2}}{{(x - 1)^2}}\):
Step 1: Determine the degree of the numerator and the denominator:
- Degree of the numerator = 1 (linear term)
- Degree of the denominator = 2 (quadratic term)
Since the degree of the numerator is less than the degree of the denominator, the fraction is proper.
Step 2: Express the proper fraction in partial fractions:
\(\frac{{x + 2}}{{(x - 1)^2}} = \frac{A}{{x - 1}} + \frac{B}{{(x - 1)^2}}\).
Step 3: Find the values of A and B:
Multiply both sides of the equation by \(((x - 1)^2)\) to eliminate the denominators:
(x + 2) = A(x - 1) + B.
Expand the equation and collect like terms:
x + 2 = Ax - A + B.
Equate the coefficients of like terms:
Coefficient of x: 1 = A.
Constant term: 2 = -A + B.
Solve the system of equations to find the values of A and B:
From the coefficient of x, A = 1.
Substituting A = 1 into the constant term equation: 2 = -1 + B, we find B = 3.
Therefore, the partial fraction decomposition is:
\(\frac{{x + 2}}{{(x - 1)^2}} = \frac{1}{{x - 1}} + \frac{3}{{(x - 1)^2}}\).
b) \(\frac{{4x^2 - 31x + 59}}{{(x - 4)^2}}\):
Step 1: Determine the degree of the numerator and the denominator:
- Degree of the numerator = 2 (quadratic term)
- Degree of the denominator = 2 (quadratic term)
Since the degree of the numerator is equal to the degree of the denominator, the fraction is proper.
Step 2: Express the proper fraction in partial fractions:
\(\frac{{4x^2 - 31x + 59}}{{(x - 4)^2}} = \frac{A}{{x - 4}} + \frac{B}{{(x - 4)^2}}\).
Step 3: Find the values of A and B:
Multiply both sides of the equation by \(((x - 4)^2)\) to eliminate the denominators:
(4x^2 - 31x + 59) = A(x - 4) + B.
Expand the equation and collect like terms:
4x^2 - 31x + 59 = Ax - 4A + B.
Equate the coefficients of like terms:
Coefficient of \(x^2\): 4 = 0 (No \(x^2\) term on the right side).
Coefficient of x: -31 = A.
Constant term: 59 = -4A + B.
Solve the system of equations to find the values of A and B:
From the coefficient of x, A = -31.
Substituting A = -31 into the constant term equation: 59 = 4(31) + B, we find B = -25.
Therefore, the partial fraction decomposition is:
\(\frac{{4x^2 - 31x + 59}}{{(x - 4)^2}} = -\frac{{31}}{{x - 4}} - \frac{{25}}{{(x - 4)^2}}\).
The above steps provide the solution for each part, including determining if the fraction is proper or improper and expressing it in partial fractions.
For more questions on algebraic fraction:
https://brainly.com/question/11875858
#SPJ8
The scale on a map is 1:320000
What is the actual distance represented by 1cm?
Give your answer in kilometres.
Answers
By answering the presented question, we may conclude that Therefore, 1 expressions cm on the map corresponds to a real distance of 3.2 km.
what is expression ?In mathematics, an expression is a collection of integers, variables, and complex mathematical (such as arithmetic, subtraction, multiplication, division, multiplications, and so on) that describes a quantity or value. Phrases can be simple, such as "3 + 4," or complicated, such as They may also contain functions like "sin(x)" or "log(y)". Expressions can be evaluated by swapping the variables with their values and performing the arithmetic operations in the order specified. If x = 2, for example, the formula "3x + 5" equals 3(2) + 5 = 11. Expressions are commonly used in mathematics to describe real-world situations, construct equations, and simplify complicated mathematical topics.
Scale 1:
320000 means that 1 unit on the map represents his 320000 units in the real world.
To find the actual distance represented by 1 cm on the map, you need to convert the units to the same scale.
1 kilometer = 100000 cm
So,
1 unit on the map = 320000 units in the real world
1 cm on the map = (1/100000) km in the real world
Multiplying both sides by 1 cm gives:
1 cm on the map = (1/100000) km * 320000
A simplification of this expression:
1 cm on the map = 3.2 km
Therefore, 1 cm on the map corresponds to a real distance of 3.2 km.
To know more about expressions visit :-
https://brainly.com/question/14083225
#SPJ1
Find the area of the following figure:

Answers
Answer:
91 cm squared
Step-by-step explanation:
Find the area of the rectangle 7 x 10=70
Triangle are (6 x 7)/2=21
Add 21+70=91
Answer:
91
Step-by-step explanation:
work out the area of the circle
take pi to be 3.142 give your answer to 1 decimal place
radius 8
Answers
The area of the circle with the given radius is 201.088 square units.
What is area of a circle?The area of a circle is the space occupied by the circle in a two-dimensional plane. Alternatively, the space occupied within the boundary/circumference of a circle is called the area of the circle. The formula for the area of a circle is A = πr², where r is the radius of the circle.
Given that, the radius of a circle is 8 units.
Here, area of a circle
= 3.142×8²
= 3.142×64
= 201.088 square units
Therefore, the area of the circle is 201.088 square units.
Learn more about the area of a circle here:
brainly.com/question/28642423.
#SPJ9
Help with algebra class please

Answers
Answer:
t=6.8
Step-by-step explanation:
t=2.01[squareroot(L)]
L=11.56
t=2.01[squareroot(11.56)]
t=2.01(3.4)
t=6.834
(round to nearest tenth)
t=6.8
(GIVING BRAINLIEST!!)
Solve the equation using equivalent fractions. SHOW YOUR WORK
4/5 + 3/15 - 2/3
Answers
Answer:
0.3 or 1/3
Step-by-step explanation:
add 4/5 + 3/15=1
then 1-2/3 = 1/3
Answer: 1/3
\(\frac{4}{5}+\frac{3}{15}-\frac{2}{3}\\\\=\frac{4}{5}+\frac{3}{3.5}-\frac{2}{3}\\\\=\frac{4}{5}+\frac{1}{5}-\frac{2}{3}\\\\=1-\frac{2}{3}\\\\=\frac{3}{3}-\frac{2}{3}\\\\=1/3\)
Step-by-step explanation:
Write an equation, and express the product in standard form.
3 copies of 5 tenths
=
x
=
Answers
Answer: 3 copies of 5 tenths = 3*0.5 = 1.5
Step-by-step explanation:
Ok, if we have:
"3 copies of a number B"
This is written as:
3*B
And we have that the number B is "5 tenths"
Now, a tenth is the first digit after the decimal point.
Then 5 tenths = 5*0.1 = 0.5
B = 0.5
3 copies of 5 tenths = 3*0.5 = 1.5
If h = 12 units and r = 4 units, what is the volume of the cone shown above? Use 3.14 for .
Answers
Answer:
200.96 units
Step-by-step explanation:
Use the formula for the volume of a cone \(V=\pi r^{2} \frac{h}{3}\)
Plug in the values (\(\pi\)=3.14) and multiply them all out
Answer:
≈ 201
Step-by-step explanation:
V= πr²h/3
V= 3.14*4²*12/3= 200.96 ≈ 201
please help me thank you in advance ❤️

Answers
Answer:
y= -1/2x-1
Step-by-step explanation:
the dimension of the confirms room or 7.2 M * 11 M what is the area of the conference room
Answers
Step-by-step explanation:
Just multiply the two dimensions to get m^2 area
7.2 m * 11 m = 79.2 m^2
(40 points) A. the silver star trucking company needs at least 3 55 gallon barrels of brake fluid and 4 barrels of oil to operate next month. They have at most 1500 to spend and a barrel of brake fluid costs 125 and a barrel of oil costs 150
B. Can the owner purchase 8 barrels of brake fluid and 4 barrels of oil for no more than 1500
If you can only do one that's fine
Answers
Answer:
No they would be $100 short.
Step-by-step explanation:
The cost of insurance can vary wildly between insurance companies. True or False
Answers
Answer:
The answer will be True
Step-by-step explanation:
Because I said so
Among all pairs of numbers whose sum is 24, find a pair whose product is as large as possible. Show the work(the steps)! Write an equation of the corresponding quadratic function. How parabola opens? What is the maximum product? Does this function has a maximum value or the minimum value? Explain. Graph the function and upload the image.
Answers
The pair of numbers that yields the maximum product when their sum is 24 is (12, 12), and the maximum product is 144. The corresponding quadratic function is P(x) = -x^2 + 24x, and the parabola opens downwards.
To find a pair of numbers whose sum is 24 and whose product is as large as possible, we can use the concept of maximizing a quadratic function.
Let's denote the two numbers as x and y. We know that x + y = 24. We want to maximize the product xy.
To solve this problem, we can rewrite the equation x + y = 24 as y = 24 - x. Now we can express the product xy in terms of a single variable, x:
P(x) = x(24 - x)
This equation represents a quadratic function. To find the maximum value of the product, we need to determine the vertex of the parabola.
The quadratic function can be rewritten as P(x) = -x^2 + 24x. We recognize that the coefficient of x^2 is negative, which means the parabola opens downwards.
To find the vertex of the parabola, we can use the formula x = -b / (2a), where a = -1 and b = 24. Plugging in these values, we get x = -24 / (2 * -1) = 12.
Substituting the value of x into the equation y = 24 - x, we find y = 24 - 12 = 12.
So the pair of numbers that yields the maximum product is (12, 12). The maximum product is obtained by evaluating the quadratic function at the vertex: P(12) = 12(24 - 12) = 12(12) = 144.
Therefore, the maximum product is 144. This quadratic function has a maximum value because the parabola opens downwards.
To graph the function, you can plot several points and connect them to form a parabolic shape. Here is an uploaded image of the graph of the quadratic function: [Image: Parabola Graph]
For more such question on function. visit :
https://brainly.com/question/11624077
#SPJ8
if the are 5 buses and the quatation amount is R8,100 how much will each person pay
Answers
Answer:
R1620
Step-by-step explanation:
1620 ×1=1620
1620×2=3240
1620×3=4860
1620×4=6480
1620×5=8100
bruce spins a spinner that has 4 equal sections of blue, red, red and green. he will also roll a 6-sides number cube what is the probability that bruce will spin a red and roll an even number

Answers
Answer:
D. You were correct.
Step-by-step explanation:
The even numbers on a 6 sided dice are 2 4 6 or 3/6 which is 1/2
The spinner has 2 red sections out of 4. The probability of getting a red is 2/4 = 1/2
P(even and red) = 1/2 * 1/2 = 1/4
I don't know what the table is for.
Which of the following statements is true regarding that equation |x+3|-2=k?

Answers
The true statement is if k = - 1 there are solutions, but if k = - 3 there are no solutions
How to determine which statement is true regarding the equation |x+3|-2=k?
Given: |x+3|-2=k
Below are rules for solving absolute value equations:
1. If p is positive and |y| = p, then
x = p OR y = -p
(two equations are set up)
2. If p is negative and |y| = p, then
No solution
3. If p is zero and |y| = p, then
One solution
Using the rules:
|x+3|-2=k
when k = -1
|x+3|-2= -1
|x+3| = 1
Rule 1 is applicable here. Thus, there are solutions
when k = -3
|x+3|-2 = -3
|x+3| = -1
Rule 3 is applicable here. Thus, no solution
Therefore, if k = - 1 there are solutions, but if k = - 3 there are no solutions. The 2nd option is the true statement
Learn more about absolute value equation on:
brainly.com/question/28728226
#SPJ1
Could someone answer the question with the photo linked below? Then explain how to solve it?

Answers
Answer:
b = sqrt(57)
Step-by-step explanation:
Since this is a right triangle, we can use the Pythagorean theorem
a^2 + b^2 = c^2 where a and b are the legs and c is the hypotenuse
8^2 + b^2 = 11^2
64+ b^2 = 121
Subtract 64
b^2 = 121-64
b^2 =57
Take the square root of each side
b = sqrt(57)
Raheem's rollerblades cost $70.25 less than his bicycle. His rollerblades cost $43.50. how much did his bicycle (B) cost?
Answers
Answer:
$113.75
Step-by-step explanation:
First add 70.25 to 43.50 to get 113.75
Answer:
$113.75
Step-by-step explanation:
b-70.25=43.50
add 70.25 to each side ..
b-70.25=43.50
+70.25+70.25
simpilfy...b=113.75
1. Solve using long division.
(9x3 - 48x2 + 13x + 3) = (x - 5)
9x2 – 3x – 2, R-7
O
9x2 - 2x - 2, R-6
9x2 - 4x - 2, R-8
9x2 - x - 2, R-5
Answers
Answer:
9x^2 - 3x - 2, R -7.
Step-by-step explanation:
x - 5) 9x^3 - 48x^2 + 13x + 3(9x^2 - 3x - 2 <---- Quotient.
9x^3 - 45x^2
- 3x^2 + 13x
-3x^2 + 15x
-2x + 3
-2x + 10
-7 <----- Remainder
PLZ HELP ME I REALLY NEED IT?!?

Answers
Answer:
he bought 17 book.
If f(x)=x^2, find f(-3)
Answers
Answer: f(-3) = 9
Step-by-step explanation:
Plug in -3 for x
f(-3) = (-3)^2
Square -3
(-3)^2 = 9
Answer:
f(-3)=9
Step-by-step explanation:
f(x)=\(x^{2}\)
To find f(-3) replace x in the function by -3
Therefore:
f(−3)=(−3)^2
=−1^2 × 3^2 =1 × 9 = 9
HOPE THIS HELPS
HAVE A GOOD DAY:)
what is the answer to 1/2 ÷2 as a fraction
Answers
Answer:
1/4
Step-by-step explanation:
1/2 ÷ 2 = 1/4
Answer:
0.25 which is 1/4.
you're welcome(:
also please give brainliest.
Step-by-step explanation:
Find the intercepts of the line

Answers
Answer:
x-int=-40
y-int=15
Step-by-step explanation:
we have points 0,15 and -40,0 on the line.
It is as easy as the y-int being 15 and the x-int being -40!
the y-int will always be= (0,#)
the x-int will always be (#,0)
You are choosing between two health clubs club a offers membership for a fee of $13 plus a monthly fee of $28 club B offers membership for a fee of $19 plus a monthly fee of $27 after how many months will the total cost of each health club be the same? What will be the total cost for each club?
Answers
To determine when the total cost of each health club will be the same, we can set up an equation and solve for the number of months.
Let's assume the number of months is represented by 'x'.
For Club A, the total cost is given by:
Total cost of Club A = $13 (one-time fee) + $28x (monthly fee)
For Club B, the total cost is given by:
Total cost of Club B = $19 (one-time fee) + $27x (monthly fee)
To find the number of months when the total cost is the same, we set the two equations equal to each other:
$13 + $28x = $19 + $27x
Simplifying the equation, we get:
$28x - $27x = $19 - $13
$x = 6
Therefore, after 6 months, the total cost of each health club will be the same.
To find the total cost for each club after 6 months, we substitute the value of 'x' back into the equations:
Total cost of Club A after 6 months = $13 + $28(6) = $13 + $168 = $181
Total cost of Club B after 6 months = $19 + $27(6) = $19 + $162 = $181
So, the total cost for both Club A and Club B will be $181 after 6 months.
For such more question on equation
https://brainly.com/question/29174899
#SPJ8
a plant has an initial height of 7 inches and grows at a constant rate of 3 inches each year. a second plant also grows at a constant rate has an initial height of 2 inches and is 14 inches tall after 3 years. after how many years are the plants the same height.
Answers
Let "x" be the number of years it takes for the two plants to be the same height.The first plant has an initial height of 7 inches and grows at a constant rate of 3 inches each year. So, the two plants will be the same height after 5 years.
Therefore, after "x" years, its height will be:7 + 3xThe second plant also grows at a constant rate and has an initial height of 2 inches. After 3 years, its height is 14 inches.
Therefore, its rate is: Rate = (Final height - Initial height) / TimeRate = (14 - 2) / 3Rate = 12 / 3Rate = 4So, after "x" years, the second plant's height will be:2 + 4x.
To find when the plants are the same height, we can set the expressions for their heights equal to each other:7 + 3x = 2 + 4xSolving for "x":3x - 4x = 2 - 73x = -5x = -5/(-1). Therefore, x = 5, the two plants will be the same height after 5 years.
For more questions on: constant
https://brainly.com/question/27983400
#SPJ8
Add quotation marks to the
sentence.
Take out your pencil, said
the teacher.
Answers
Step-by-step explanation:
9+10....................................................................
Answers
Answer:
24234221111111111111111111111
Step-by-step explanation:
