Find P 20 of the following arithmetic sequence: 206, 212, 218, 224....
State:
Po =
d =
P20 =
Answers
Answer:
\(p_{20} = 1.25528\)
P₀ = 206 and difference d = 6
Step-by-step explanation:
Step(i):-
Given that the arithmetic sequence
206,212,218,224,.....
P₀ = 206 and difference d = 212-206 = 6
The \(n^{th}\) term of the sequence
\(t_{n} = ar^{n-1}\)
Step(ii):-
The \(n^{th}\) term of the sequence
\(P_{n} = ar^{n-1}\)
Put n=20
\(P_{20} = 206 ( 6) ^{20-1}\)
\(p_{20} = 1.25528\)
Related Questions
Madison took a taxi from her house to the airport. The taxi company charged a pick-up fee of $3.20 plus $5 per mile. The total fare was $98.20, not including the tip. Write and solve an equation which can be used to determine
m
m, the number of miles in the taxi ride.
Answers
Answer:
19 miles
Step-by-step explanation:
y = mx + b
y = the total cost
m = the number of miles
x = the cost per mile
b = pick-up fee
98.20 = m(5) + 3.20 Subtract 3.20 from 98.2
95 = 5m divide both sides by 5
19 = m
If the taxi company charged a pick-up fee of $3.20 plus $5 per mile and the total fare was $98.20 the equation representing the given relation is 98.20 = m(5) + 3.20 and the obtained value of m is 19 miles.
What is a linear equation?It is defined as the relation between two variables, if we plot the graph of the linear equation we will get a straight line.
If in the linear equation, one variable is present, then the equation is known as the linear equation in one variable.
It is given that the taxi company charged a pick-up fee of $3.20 plus $5 per mile and the total fare was $98.20.
If m, is the number of miles in the taxi ride, y represents the total fare, x represents the charge per mile and b represents the pickup charge.
y = mx+ b
98.20 = m(5) + 3.20
5m = 98.20 - 3.20
95 = 5m
19 = m
Thus, if the taxi company charged a pick-up fee of $3.20 plus $5 per mile. The total fare was $98.20 the equation representing the given relation is 98.20 = m(5) + 3.20 and the obtained value of m is 19 miles.
Learn more about the linear equation here:
brainly.com/question/11897796
#SPJ2
Find the missing sides
Someone do this for me

Answers
The missing parts of the triangles are found below.
What are the missing parts?1) Cos 34 = x/13
x = 13Cos 34
= 12.9
2) Sin 43 = x/19
x = 19Sin 43
= 13
3) Cos 65 = 16/x
x = 16/Cos 65
= 38
4) Cos 47 = x/13
x = 13Cos 47
= 9
5) Sin 57 = 20/x
x = 20/Sin57
x = 24
6) Sin 69 = 11/x
x = 11/Sin 69
= 12
7) Cos 22 = 12/x
x = 12/Cos 22
x = 13
8) Sin 26 = 17/x
x = 12/Sin 26
x = 27
9) Sin 38 = 17/x
x = 17/Sin 38
x = 28
These are the parts that we need to find in the triangles above.
Learn more about triangle:https://brainly.com/question/2773823
#SPJ1
Find the value of x. Write your answer in simplest form.

Answers
Answer:
\(x = \frac{9}{ \sqrt{2} } = \frac{9 \sqrt{2} }{2} \)
I need help fast smart people I need your answer

Answers
Answer:
The angle D is 64 degrees.
Step-by-step explanation:
This is because they are vertical
Answer:
i think its the yellow square
Step-by-step explanation:
Identify the exponential function whose graph is shown below.

Answers
Answer:
The exponential function is
\(y = {2}^{x} \)
Lisa and Mark are selling flower bulbs for a school fundraiser. Customers can buy bags of tulip bulbs and bags of daffodil bulbs. Lisa sold 4 bags of tulip bulbs and 8 bags of daffodil bulbs for a total of $176. Mark sold 8 bags of tulip bulbs and 6 bags of daffodil bulbs for a total of $192. Determine the system of equations that would allow you to find the cost each of one bag of tulip bulbs (t) and one bag of daffodil bulbs (d).
(giving brainliest pls help)
Answers
The system of equations that allows finding the cost of each bag of tulip bulbs (t) and each bag of daffodil bulbs (d) are:
L = 4t + 8d = 176M = 8t + 6d = 192.What is a system of equations?A system of equations refers to simultaneous equations, which are two or more equations that must be solved together.
Equations:Tulip Daffodil Total Sales
Lisa's sales 4 8 $176
Mark's sales 8 6 $192
Lisa's sales, L = 4t + 8d = 176 ... equation 1
Mark's sales, M = 8t + 6d = 192 ... equation 2
Solution:Multiply equation 1 by 2:
8t + 16d = 352 ... equation 3
Subtract equation 2 from equation 3:
8t + 16d = 352
- 8t + 6d = 192
= 10d = 160 (352 - 192)
d = 16 (160/10)
Substitute d in either equation 1 or 2, to get t:
8t + 6d = 192
8t + 6(16) = 192
8t + 96 = 192
8t = 96
t = 12 (96/8)
Check: Equation 1:4t + 8d = 176
= 4(12) + 8(16) = 176
= 48 + 128 = 176
176 = 176
Thus, the cost of each bag of tulip bulbs (t) is $12, while the cost of one bag of daffodil bulbs (d) is $16 based on the system of equations above.
Learn more about the system of equations at https://brainly.com/question/13729904
#SPJ1
A man gave 90000.00 to his two daughters Jane and Lydia, 75.00 was given to Lydia to pay her load. After sharing the money Lydia has twice as
much as Jane. How much did each received?
Answers
Jane received $30025 and Lydia received $60000. Let's assume the amount of money that Jane received as x; then Lydia's share of the money will be twice the share of Jane.
We are to find out the share of each person. Here is the solution in steps:Suppose Jane's share was x dollars, and Lydia's share was y dollars.
Given that the total amount given to the two daughters was $90000. Also, given that Lydia paid off her $75, hence she got $75 less than Jane.
Therefore, y = 2x - 75; this is because we are given that Lydia got twice the share of Jane, and also, she got $75 less than Jane. Hence, x + y = $90000, this is because the total sum of money shared is $90000.
Substituting y = 2x - 75 into x + y = $90000 gives x + (2x - 75) = $90000.
Simplifying, we have :3x = $90000 + 75 = $90075.
Dividing both sides by 3, we get:x = $30025. Hence, Jane's share is $30025 Lydia's share = 2x - 75 = 2($30025) - $75 = $60075 - $75 = $60000.
Therefore, Jane received $30025 and Lydia received $60000.
For more question on amount
https://brainly.com/question/25720319
#SPJ8
PLEASE ANSWER FAST
Find the square root of 16.
O a
-4
Ob
4
Ос
+4
Od
-8
Answers
Answer:
the square root of 16 is 4
Petra has a second larger box that is 6 inches by 8 inches by 4 inches. How many times larger is the volume of this second box? The surface area?
Answers
Answer:
volume is 8 times larger and surface area is about 2.7 times larger
Step-by-step explanation:
a)24 in³ b) 76 in² c) volume is 8 times larger and surface area is about 2.7 times larger.
Based on the supply graph and the demand graph shown above, what is the price at the point of equilibrium?
Hint: Think about the point where they both meet. For example, if you were to place the graphs on top of each other, what would be the point of intersection?
Type the correct number below without the dollar sign.

Answers
Based on the supply graph and demand graph shown above, the price at the point of equilibrium is $ 30.
Demand refers to quantity of a commodity that the consumers are willing to, able to purchase at a given price during a given period of time. Supply refers to quantity of a commodity that the producers are willing to, able to offer for sale at a given price during a given period of time.
Demand curve slopes downward due to inverse relationship between price and quantity demanded whereas supply curve slopes upward due to direct relationship between quantity supplied and price. When both demand and supply curve intersect with each other balance is achieved. Intersection point between demand and supply curve is known as equilibrium.
At this point when prices are equal is known as equilibrium price and when quantiy demanded or supplied are equal it is known as equilibrium quantity. When we combine the given graph. Equilibrium is achieved at a point when price is equal to $ 30 and quantity is equal to 20 units.
To learn more about equilibrium of demand and supply:
https://brainly.com/question/30237240
pleaseee helppp mede

Answers
Answer:
148
Step-by-step explanation:
A and B are alternate exterior angles and alternate exterior angles are equal when the lines are parallel
A = B
6x-2 = 4x+48
Subtract 4x from each side
6x-4x-2 = 4x+48-4x
2x-2 = 48
Add 2 to each side
2x-2 +2 = 48+2
2x = 50
Divide by 2
2x/2 = 25
We want to find angle A
A = 6x-2
= 6*25 -2
150 -2
= 148
Answer:
Solution given:
<A=<B{alternate exterior angle are equal}
6x-2=4x+48
6x-4x=48+2
2x=50
x=50/2
x=25
<A=6×25-2=148°
On November 1st, Halloween candy is discounted 60%. If the original price of a bag of candy corn was $5, what is the final price of the candy, including the discount and a 10% sales tax?
Answers
Answer:
$2.20
Step-by-step explanation:
Original price (before discount and before tax): $5
Discount is 60%.
Amount of discount is: 60% of $5 = 0.6 × $5 = $3
Price after 60% discount: $5 - $3 = $2
Tax is 10%.
Amount of tax is: 10% of $2 = 0.1 × $2 = $0.20
Final price = price after discount + tax = $2.00 + $0.20 = $2.20
A percentage is a way to describe a part of a whole. The final price of the candy, including the discount and a 10% sales tax is $2.2.
What are Percentages?A percentage is a way to describe a part of a whole. such as the fraction ¼ can be described as 0.25 which is equal to 25%.
To convert a fraction to a percentage, convert the fraction to decimal form and then multiply by 100 with the '%' symbol.
Given that the cost of the candy is $5 and a 60% discount is given on the candy. Therefore, the price of the candy after the discount will be,
Discounted price = Price - 60% of price
= $5 - 0.60($5)
= $5 - $3
= $2
Now, on the price of the candy 10% sales tax will be added. Therefore, the Price of the candy after adding Tax will be,
Taxed price = Discounted price + 10% of discounted price
= $2 + 0.10($2)
= $2 + $0.2
= $2.02
Hence, the final price of the candy, including the discount and a 10% sales tax is $2.2.
Learn more about Percentages here:
https://brainly.com/question/6972121
#SPJ2
write an equation in slope intercept form that passes through the given point and is perpendicular to the graph of given equation (1,-2) y=5x+4
Answers
The equation of the line perpendicular to y = 5x + 4, passing through the point (1, -2), is y = (-1/5)x - 9/5.
To find an equation in slope-intercept form that passes through the point (1, -2) and is perpendicular to the given equation y = 5x + 4, we need to determine the slope of the perpendicular line.
The given equation y = 5x + 4 is already in slope-intercept form (y = mx + b), where m represents the slope. In this case, the slope of the given line is 5.
To find the slope of a line perpendicular to this, we use the fact that the product of the slopes of two perpendicular lines is -1. So, the slope of the perpendicular line can be found by taking the negative reciprocal of the slope of the given line.
The negative reciprocal of 5 is -1/5.
Now that we have the slope (-1/5) and a point (1, -2), we can use the point-slope form of the equation:
y - y1 = m(x - x1)
Substituting the values:
y - (-2) = (-1/5)(x - 1)
Simplifying:
y + 2 = (-1/5)(x - 1)
To convert the equation into slope-intercept form (y = mx + b), we need to simplify it further:
y + 2 = (-1/5)x + 1/5
Subtracting 2 from both sides:
y = (-1/5)x + 1/5 - 2
Combining the constants:
y = (-1/5)x - 9/5
Therefore, the equation of the line perpendicular to y = 5x + 4, passing through the point (1, -2), is y = (-1/5)x - 9/5.
For more question on perpendicular visit:
https://brainly.com/question/1202004
#SPJ8
the difference between two numbers is 9 and the product and the product of the number is 162 find the two numbers
Answers
Answer:
the two numbers are x = -81 - 81*sqrt(7) and y = (-1 - sqrt(7)) / 2.
Step-by-step explanation:
To find the two numbers, we can use the formula for the sum of two numbers:
x + y = z
Where x and y are the two numbers and z is their sum.
In this case, we know that the difference between the two numbers is 9, so we can set x to be the larger of the two numbers and y to be the smaller number:
x - y = 9
We can also use the fact that the product of the two numbers is 162 to set up an equation:
xy = 162
Now we can solve for x and y by substituting the second equation into the first and solving for x:
x = 162/y
Substituting this expression for x into the first equation gives us the following:
(162/y) - y = 9
We can simplify this equation to:
162 - y^2 = 9
We can solve for y by completing the square:
y^2 - y + 4.5 = 0
We can use the quadratic formula to find the solutions for y:
y = (1 +/- sqrt(1 - 414.5)) / (2*1)
This simplifies to:
y = (-1 +/- sqrt(7)) / 2
Since y is the smaller number, we need to choose the negative solution:
y = (-1 - sqrt(7)) / 2
We can use this value of y to find the value of x:
x = 162/y = 162/(-1 - sqrt(7))/2
This simplifies to:
x = (-81 - 81*sqrt(7))/2
So the two numbers are x = -81 - 81*sqrt(7) and y = (-1 - sqrt(7)) / 2.
Answer:
9, 18
Step-by-step explanation:
lets say the smaller number is x, then the larger number is x+9
we know x * (x+9) = 162.
expand to get x^2 + 9x - 162 = 0, factor or use the quadratic formula to get x^2 + 9x -162 = (x + 18) (x - 9) = 0, so x = 9 or -18.
I'm assuming the two numbers must be positive, so x = 9, and the larger number is 9+9 = 18.
F(x)=-x2-7x-5
Find f(-5)
Answers
Answer:
f(-5)=5
Step-by-step explanation:
the "-5" is telling us what to plug in for x. So, the new equation would be:
f(-5)= -(-5)^2-7(-5)-5
if we reduce, the expression would be
-25+35-5
our final answer would be 5.
Is the following function one to one? f(x) = (x + 2)²
Yes No
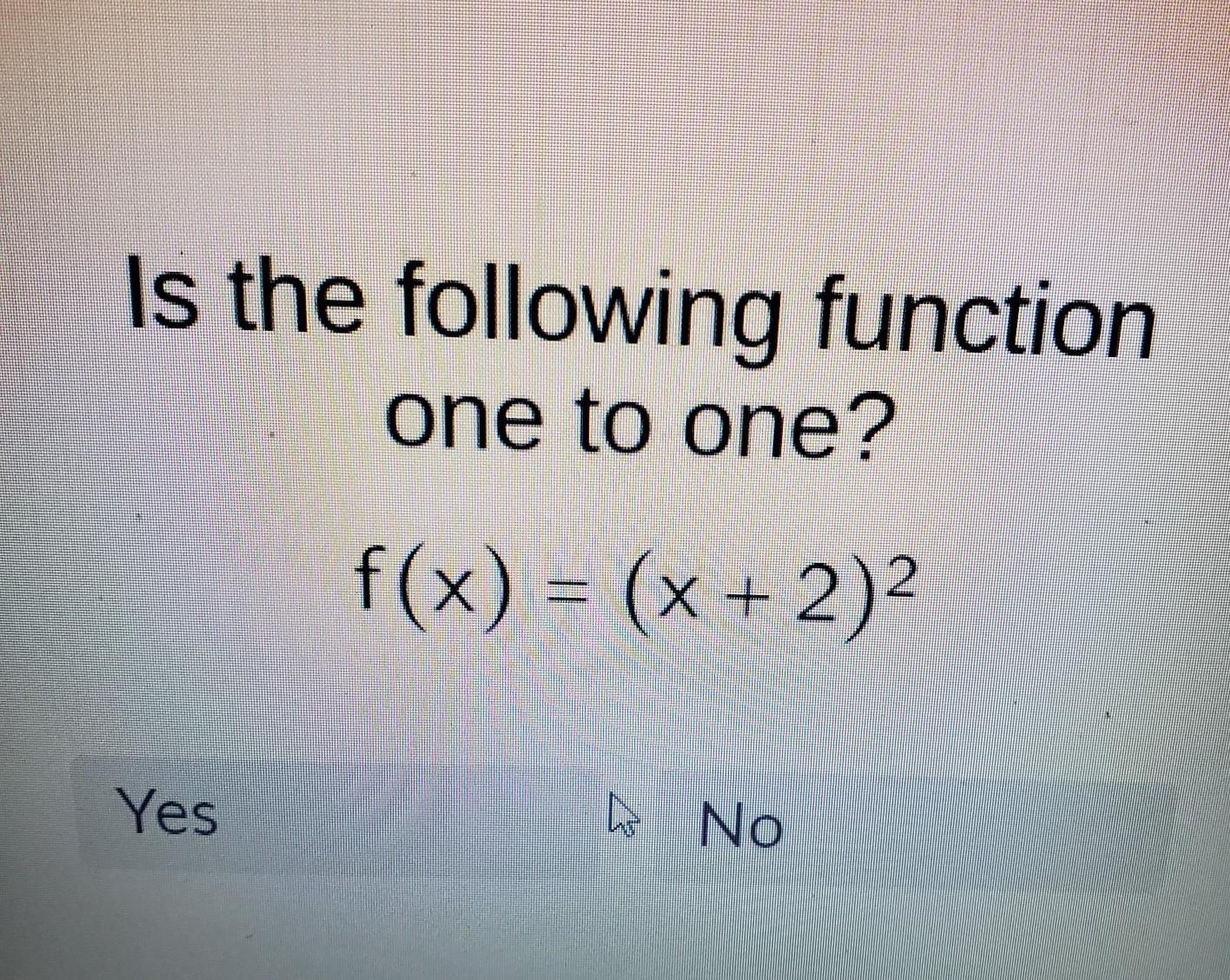
Answers
Answer:
Yes, the function f(x) = (x + 2)² is one-to-one.
A spinner with 10 equal sized slices has 4 yellow slices, 3 red, and 3 blue slices. Kala spun the dial 1000 times and got the following results.
Answers
Kala spun the spinner 1000 times and got the following results:
- Yellow: 400 times
- Red: 300 times
- Blue: 300 times
1. Calculate the amount of sales tax:
- The item costs $350 before tax.
- The sales tax rate is 14%.
- To find the sales tax amount, multiply the cost of the item by the tax rate:
Sales tax = $350 * 0.14 = $49.
2. Determine the total cost of the item including tax:
- Add the sales tax amount to the original cost of the item:
Total cost = $350 + $49 = $399.
3. Analyze the spinner results:
- The spinner has 10 equal-sized slices.
- There are 4 yellow slices, 3 red slices, and 3 blue slices.
- Kala spun the dial 1000 times.
4. Calculate the frequency of each color:
- Yellow: Kala got 400 yellow results out of 1000 spins.
- Red: Kala got 300 red results out of 1000 spins.
- Blue: Kala got 300 blue results out of 1000 spins.
5. Calculate the probability of landing on each color:
- Yellow: Probability = Frequency of yellow / Total spins = 400 / 1000 = 0.4.
- Red: Probability = Frequency of red / Total spins = 300 / 1000 = 0.3.
- Blue: Probability = Frequency of blue / Total spins = 300 / 1000 = 0.3.
For more such questions on spinner, click on:
https://brainly.com/question/32737567
#SPJ8
There are blue and red balls in a box.4/7 of the balls are blue.If there are 28 balls in a box ,how many of them are red
Answers
Answer:
16
Step-by-step explanation:
can't really explain it but it's 16 trust me
Answer:
12Step-by-step explanation:
4/7 balls are blue
so 3/7 are red
28/7=4
4 x 3=12
Solve the equation using the Properties of Equality.
79 + 3 = 45
Step 1 out of 4:
7a + 3 - [ ] = 45- [ ]
Answers
Answer:
7a + 3 -3 =45 - 3
7a + 0 = 42
7a = 42
7a/7 = 42/7
a = 6
When the price of Xis RM4 and the price of Y is RM10, which of the following combinations would be the intercept of axes
(X,Y) if you have an income of RM 100?
Select one:
A. (25X, 10Y)
B. (20X, 5Y)
C. (10X, 25Y)
D. (5X, 20Y)
Answers
li walks at a contant rrate of 7 ft in 4 s the table shows the relation ship of the feet to seconds what is the constant proportionality for the relationship of feet to minutes
Answers
Answer:
105ft per minute
Step-by-step explanation:
well, if he/she walks 7ft in 4s, then you divide 60/4. In which you get 15.
15•7=105
Write 13.13.13.13.13 in exponential form?
Answers
13.13.13.13.13 in exponential form is 13^5
How to rewrite the expression?The expression is given as:
13.13.13.13.13
The factors of the above expression are 13.
And each factor is grouped by product
There are five 13s in the expression.
So, we have:
13.13.13.13.13 = 13^5
Hence, 13.13.13.13.13 in exponential form is 13^5
Read more about exponential form at:
https://brainly.com/question/2456547
#SPJ1
The quotient of a number and 19 is 5. Find the number.
Answers
Answer:
95
Step-by-step explanation:
Take the missing number as x.
Then the required value of x will be,
→ x ÷ 19 = 5
→ x = 5 × 19
→ [ x = 95 ]
Hence, the number is 95.
Answer:
x ÷ 9
= 5
x = 5 × 19
x = 95
Hance,the number is 95

using the line of best fit

Answers
The monthly cell phone bill when shared data equals zero is given as follows:
$26.
How to define a linear function?The slope-intercept representation of a linear function is given by the equation presented as follows:
y = mx + b
The coefficients of the function and their meaning are described as follows:
m is the slope of the function, representing the change in the output variable y when the input variable x is increased by one.b is the y-intercept of the function, which is the initial value of the function, i.e., the numeric value of the function when the input variable x assumes a value of 0. On a graph, it is the value of y when the graph of the function crosses the y-axis.The intercept of the line in this problem is given as follows:
b = 26.
Hence $26 is the monthly cell phone bill when shared data equals zero.
More can be learned about linear functions at https://brainly.com/question/24808124
#SPJ1
A system of equations is given.
Equation 1: 4x − 6y = 10
Equation 2: 9x + 2y = 7
Explain how to eliminate x in the system of equations.
Answers
Step-by-step explanation:
To eliminate x in the system of equations:
1. Multiply Equation 1 by 9 and multiply Equation 2 by -4, this gives:
Equation 1: 36x -54y = 90
Equation 2: -36x - 8y = -28
2. Add the two equations together to eliminate x:
(36x - 54y) + (-36x - 8y) = 90 - 28
Simplifying, we get:
-62y = 62
3. Solve for y:
y = -1
4. Substitute y = -1 into one of the original equations, say Equation 1:
4x - 6(-1) = 10
Simplifying, we get:
4x + 6 = 10
5. Solve for x:
4x = 4
x = 1
Therefore, the solution to the system of equations is x = 1 and y = -1. We can check that these values are correct by substituting them back into the original equations and verifying that they satisfy both equations.
14. A pole has two wires attached to it, one on each side, forming two right triangles as shown.
How tall is the pole?
26.8 feet
25.7feet
29.6 feet
22.3 feet

Answers
If a pole has two wires attached to it, one on each side, forming two right triangles as shown, then the height of the pole is 29.6 feet
Consider the triangle on left hand side
The length of the base = 34 feet
The measure of angle = 41 degrees
Opposite side is the height of the pole
Here we have to use the trigonometric functions
sin θ = Opposite side / Hypotenuse
cos θ = Adjacent side / Hypotenuse
tan θ = Opposite side / Adjacent side
Here we have to use the equation of tan θ
Substitute the values in the equation
tan 41 = Opposite side / 34 feet
Opposite side = 34 × tan 41
= 29.6 feet
Therefore, the height of the pole is 29.6 feet
Learn more about trigonometric functions here
brainly.com/question/25618616
#SPJ4
A man throws a ball off the top of a building that is 46 ft. high. The following are points on the parabola of the flight of the ball: (1, 63); (2, 48); (3, 1) What is the quadratic equation of the parabola of this flight? (Hint: 46 is the y-intercept)
Answers
The quadratic equation of the parabola representing the flight of the ball is: y = \(46x^2 - 153x + 170\)
To find the quadratic equation of the parabola representing the flight of the ball, we can use the standard form of a quadratic equation: y = \(ax^2\) + bx + c.
Given the points (1, 63), (2, 48), and (3, 1), we can substitute these values into the equation to form a system of three equations:
Equation 1: 63 =\(a(1^2) + b(1) + c\)
Equation 2: 48 =\(a(2^2) + b(2) + c\)
Equation 3: 1 = \(a(3^2) + b(3) + c\)
We can simplify these equations:
Equation 1: 63 = a + b + c
Equation 2: 48 = 4a + 2b + c
Equation 3: 1 = 9a + 3b + c
Now, we can solve this system of equations to find the values of a, b, and c. Subtracting Equation 1 from Equation 2 and Equation 3, we get:
Equation 4: 48 - 63 = 4a + 2b + c - (a + b + c)
Equation 5: 1 - 63 = 9a + 3b + c - (a + b + c)
Simplifying these equations:
Equation 4: -15 = 3a + b
Equation 5: -62 = 8a + 2b
Now, we have a system of two equations (Equation 4 and Equation 5) with two variables (a and b). Solving this system of equations, we get:
Multiply Equation 4 by 2: -30 = 6a + 2b
Subtract Equation 5 from this result: 30 - (-62) = 6a + 2b - (8a + 2b)
92 = -2a
a = -92 / -2
a = 46
Substituting the value of a into Equation 4:
-15 = 3(46) + b
-15 = 138 + b
b = -15 - 138
b = -153
Now, we have found the values of a and b. To find the value of c, we can substitute any of the given points into the equation y = \(ax^2 + bx + c.\)Let's use the point (1, 63):
63 = \(46(1^2) + (-153)(1) + c\)
63 = 46 - 153 + c
c = 63 - 46 + 153
c = 170
Therefore, the quadratic equation of the parabola representing the flight of the ball is: y =\(46x^2 - 153x + 170\)
For such more questions on quadratic equation
https://brainly.com/question/28038123
#SPJ11
An open box is to be constructed so that the length of the base is 3 times larger than the width of the base. If the cost to construct the base is 4 dollars per square foot and the cost to construct the four sides is 1 dollars per square foot, determine the dimensions for a box to have volume
Answers
Answer:
Step-by-step explanation:
Let assume that the volume = 88 cubic feet
Then:
\(L = 3w --- (1)volume = l \times w \times h \\ \\ 88 = (3w) \times w \times h \\ \\ 3w^2 h= 88 \\ \\ h = \dfrac{88}{3w^2}--- (2) \\ \\\)
The construction cost now is:
\(C = 4(l \times w) + 2 ( w \times h) + 2(l \times h) \\ \\ C = 4(3w^2) + 2(w \times \dfrac{88}{3w^2}) + 2(3w \times \dfrac{88}{3w^2}) \\\\ C = 12w^2 + \dfrac{176}{3w} + \dfrac{176}{w}\)
Now, to determine the minimum cost:
\(\dfrac{dC}{dw}= 0 \\ \\ \implies 24 w - \dfrac{176}{3w^2}- \dfrac{176}{w^2}=0 \\ \\ 24 w ^3 = \dfrac{176}{w^2}(\dfrac{1}{3}+1) \\ \\ 24 w ^3 = \dfrac{176(4)}{3} \\ \\ w^3 = \dfrac{88}{3(3)}\)
\(w = \dfrac{88}{3(3)}^{1/3} \ feet\)
Now;
\(length = 3 ( \dfrac{88}{3(3)})^{1/3} \ feet\)
\(height = ( 88})^{1/3} (3)^{1/3} \ feet\)
Anyone Help !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

Answers
Answer:
20181610Hope this helps18
16
10
Those are the numbers
for the forecasting process to be effective, internal data should be multiple choice highly aggregated. highly disaggregated. sampled once a year. none of the options are correct. kept on an annual basis.
Answers
For the forecasting process to be effective, internal data should be highly disaggregated
Predicting the future based on historical and current facts is the forecasting process. The most popular method for doing this is trend analysis. It is typically ideal to use internal data that is significantly disaggregated for forecasting to be successful. This means that rather than aggregating or summarizing the data at a high level, it should be broken down into as much detail as feasible.
Since highly disaggregated data presents a more complete and precise picture of the variables that may impact future events, forecasting can be done more accurately and dependably. This can include information about previous sales, manufacturing rates, inventory levels, costs, and other elements that can be important for forecasting. Whereas, using highly aggregated data can lead to less accurate and reliable forecasts, as it may not capture the full range of factors that may influence future outcomes.
Read more about forecasting on:
https://brainly.com/question/29889592
#SPJ4