ES) 12. There are 2 companies that you can rent a bike from.
Company A charges a fee of $30 plus $5 per hour to rent
their bikes. Company B charges a fee of $40 plus $4 per
hour to rent their bikes.
A. Write an expression for each company with x
representing the number of hours.
B. At how many hours is Company A the same cost
as Company B?
C. What is the cost at the number of hours from part
B?
Answers
Answer:
dghsjdxfkhc,gjmhnfgb
Step-by-step explanation:
Related Questions
Change the subject of the formula x = 3y + 6p to
р
Help please
Answers
Answer:
p=x-3y/6
Step-by-step explanation:
x=3y+6p
x-3y=6p
divide both sides by 6
P=x-3y/6
Airlines in the U.S.A average about 1.6 fatalities per month.
a) Describe a suitable probability distribution for Y, the number of fatalities per month.
b) What is the probability that no fatalities will occur during any given month?
c) What is the probability that one fatality will occur during any given month?
d) Find E(Y) and the standard deviation of Y
Answers
The expected number of fatalities per month is 1.6, and the standard deviation is approximately 1.265.
a) A suitable probability distribution for Y, the number of fatalities per month, is the Poisson distribution. The Poisson distribution is commonly used to model the number of events that occur in a fixed interval of time or space, given the average rate at which those events occur.
b) To find the probability that no fatalities will occur during any given month, we can use the Poisson distribution with λ = 1.6 (average number of fatalities per month). The probability mass function (PMF) of the Poisson distribution is given by P(Y = k) = (e^(-λ) * λ^k) / k!, where k is the number of events (fatalities) and e is the base of the natural logarithm.
For Y = 0 (no fatalities), the probability can be calculated as follows:
P(Y = 0) = (e^(-1.6) * 1.6^0) / 0! = e^(-1.6) ≈ 0.2019
Therefore, the probability that no fatalities will occur during any given month is approximately 0.2019 or 20.19%.
c) To find the probability that one fatality will occur during any given month, we can use the same Poisson distribution with λ = 1.6. The probability can be calculated as follows:
P(Y = 1) = (e^(-1.6) * 1.6^1) / 1! = 1.6 * e^(-1.6) ≈ 0.3232
Therefore, the probability that one fatality will occur during any given month is approximately 0.3232 or 32.32%.
d) The expected value (mean) of Y, denoted as E(Y), can be calculated using the formula E(Y) = λ, where λ is the average number of fatalities per month. In this case, E(Y) = 1.6.
The standard deviation of Y, denoted as σ(Y), can be calculated using the formula σ(Y) = √λ. In this case, σ(Y) = √1.6 ≈ 1.265.
Learn more about standard deviation here :-
https://brainly.com/question/29115611
#SPJ11
Point M is located at (3, 5) in the coordinate plane. Point M′ is located at (3, –5). Which statement is true?
Group of answer choices
Point M′ is 6 units from point M.
Point M′ is 8 units from point M.
Point M′ is the image produced by reflecting point M across the x-axis.
Point M′ is the image produced by reflecting point M across the y-axis.
Answers
For the problem 9 + 2(3) do you get the same final answer if you add first as you do if you multiply
first?
Answers
if you add first you get 33
9+2(3)
11(3)
33
if you multiply first you get 15
9+2(3)
9+6
15
15 would be correct because multiplication comes first in pemdas :)
Answer:
No
Step-by-step explanation:
no you do not get the same answer
This is the order in which you should approach problems, doing otherwise may lead to a wrong answer
P - parenthesis -- meaning solve whatever is the the parenthesis
E - exponents -- an example of an exponent is \(2^{3}\) which equals 8
MD - multiplication/division
AS - addition / subtraction
for our particular problem, we have
9 + 2(3)
multiplication trumps addition thus we perform multiplication first
9 + 6 = 15 ---CORRECT
if we were to addition first we would get
9 + 2(3) = 11(3) = 33 This would be WRONG
note: multiplication and division are on the same level
subtraction and addition are on the same level
if you encounter a problem like 4 ÷ 2 * 3. perform the calculation from left to right thus we would have 4 ÷ 2 = 2 and then 2 * 3 = 6
same applies for addition subtraction
Differentiate f and find the domain of f. (Enter the domain in interval notation.)
f(x) = (1/7) /(1 ? ln(x ? 5))
derivative f'(x) = ?
Domain = ?
Answers
The domain of the function is (5, e + 5) and derivative is f'(x) = 1/(7(x - 5)(1 − ln(x − 5))²).
Given the function f(x) = (1/7) /(1 − ln(x − 5)).
To differentiate f and find the domain of f, we have to use the quotient rule of derivative. The quotient rule of differentiation states that the derivative of a quotient is given by the numerator's derivative times the denominator minus the denominator's derivative times the numerator, all divided by the square of the denominator.
Hence, we can get the derivative of f(x) as follows:
f(x) = (1/7) /(1 − ln(x − 5))
Using the quotient rule of differentiation, we get
f'(x) = [(1 − ln(x − 5)) * d/dx (1/7)] − [1/7 * d/dx (1 − ln(x − 5)))]/(1 − ln(x − 5))²
= [0 − 1/7(-1/(x - 5))]/(1 − ln(x − 5))²
= [1/(7(x - 5))]/(1 − ln(x − 5))²
= 1/(7(x - 5)(1 − ln(x − 5))²)
Therefore, the derivative of f(x) is f'(x) = 1/(7(x - 5)(1 − ln(x − 5))²).
Now, to find the domain of f(x), we observe that the denominator (1 − ln(x − 5)) must be greater than 0. This is because we cannot take the natural log of a negative number. Hence, we have
1 − ln(x − 5) > 0
⇒ ln(x − 5) < 1
⇒ x − 5 < e¹= e
⇒ x < e + 5
Therefore, the domain of f is the open interval (5, e + 5).Thus, the derivative f'(x) = 1/(7(x - 5)(1 − ln(x − 5))²).
To know more about the "derivative": https://brainly.com/question/12047216
#SPJ11
Mr. and mrs. Hawell want to file their income tax return together. Which filing status should they use?

Answers
Answer:
The one that ends with jointly!
Step-by-step explanation:
Answer:
B. Married filing jointly
Step-by-step explanation:
You earn $20 for washing 5 cars how much do you earn for washing 2 cars
Answers
Answer:
$8
Step-by-step explanation:
First we have to see how much you are paid per car. To do this we divide the money earned ($20), by the number of cars washed (5).
20÷5=4
This tells us you earn $4 per car. So, to find the amount you would earn buy washing 2 cars, you multiply the money earned per car by 2.
4·2=8
This means you would earn $8.
Would you please mark my answer brainliest if it helped you? :D
help solve 90 please

Answers
Answer:
c=263
Step-by-step explanation:
Cody wanted to give each of his forty-five friends an equal amount of candy. At the store he bought six hundred eighty pieces total to give to them. How many more pieces should he have bought so he didn't have any extra pieces? I will branliest to who ever answers first!
Answers
Answer:
He should have got 40
Step-by-step explanation:
680 / 45 = 15.11
45 x 16 = 40
Please need help with #8 & 9, need urgent help,thank you!8. Suzanne told her friend Johnny that he needed to know for the calculus test that the derivative of a cubic function will always be a quadratic function. Is Suzanne correct? Explain why or why not
Answers
Suzanne is correct in stating that the derivative of a cubic function will always be a quadratic function.
Suzanne's statement is correct. A cubic function is a function of the form \(f(x) = ax^3 + bx^2 + cx + d\), where a, b, c, and d are constants.
To find its derivative, we need to differentiate each term of the function with respect to x. The derivative of a constant term d is 0, so we can ignore it. We have:
\(f'(x) = 3ax^2 + 2bx + c\)
As we can see, the derivative of a cubic function is a quadratic function of the form g(x) = \(3ax^2 + 2bx + c\).
Therefore, Suzanne is correct.
Recall that a cubic function is a function of the form\(f(x) = ax^3 + bx^2 + cx + d,\)
where a, b, c, and d are constants.
To find the derivative of this function, we need to differentiate each term with respect to x.
The derivative of a constant term d is 0, so we can ignore it.
Applying the power rule of differentiation, we get:
\(f'(x) = 3ax^2 + 2bx + c\)
As we can see, the derivative of a cubic function is a quadratic function of the form g(x) = \(3ax^2 + 2bx + c.\)
Therefore, Suzanne is correct in stating that the derivative of a cubic function will always be a quadratic function.
Learn more about quadratic function.
https://brainly.com/question/18958913
#SPJ4
What is the mode of the following list of numbers:
\left\{3,4,4,5,6,7,7,7,8,9\right\}{3,4,4,5,6,7,7,7,8,9}
8
5
7
6
Answers
Answer: Your answer is 6
Quick I need help pleaseeeeeeee "What is the sum of all interior angles of a 28-sided regular polygon?"
5,040°
4,680°
180°
167°
Answers
The sum of all interior angles of a 28-sided regular polygon is 4680°.
What is a polygon ?
The definition of a polygon is a closed, two-dimensional, plane shape created by connecting three or more line segments. During our study of geometry, polygons are a common sight.
Poly, which means "many," and gon, which means "angle," make up the Greek word "Polygon." Polygons of many kinds can be seen all around us. For instance, a honeycomb is shaped like a hexagon.
An n-sided polygon's inner angle measurements added together equal to (n-2)180°. As a result, for a polygon of 28 sides, the sum of the interior angle measurements is 26(180°) = 4680°.
To Learn more about the polygon here:
https://brainly.com/question/1592456
#SPJ1
Answer:
b) 4,680
Step-by-step explanation:
hope this helps
Solve for x. Round to the nearest tenth of a degree, if necessary. J 3.6 K 2 xº L
Answers
Solving the triangle JKL using the fact that the sum of angles in a triangle is 180 degrees, we find that x is approximately 174.4 degrees.
To solve for x in the given equation, we can use the fact that the sum of angles in a triangle is equal to 180 degrees. Since JKL is a triangle, we can write:
J + K + L = 180
Substituting the given values:
3.6 + 2 + x = 180
Simplifying the equation:
5.6 + x = 180
Subtracting 5.6 from both sides:
x = 180 - 5.6
x ≈ 174.4
Therefore, the value of x rounded to the nearest tenth of a degree is approximately 174.4 degrees.
To learn more about triangle click here
brainly.com/question/29083884
#SPJ11
PLS HELP ILL MARK AS BRAINLIEST PLSS

Answers
Answer:
10%
Step-by-step explanation:
I think it's right lol but I could be wrong I forgot a lot of this stuff
but out of all the data it goes from 22-42 so 20 points in total
there is only 2 of the data points behind 24, so it is 2/20 or 10%
X-intercept
Find f(-2)
Find x for f(x)=2

Answers
By using the graph we can see:
x-intercept: x = 0.f(-2) = 4f(x) = 2 for x = -1.3How to find the requested values?First, we want to find the value of x such that the graph touches (intercepts) the x-axis.
On the graph, we can see that it intercepts the x-axis at x = 0, so that is the x-intercept.
Now we want to find f(-2), this is the value of the function when x = -2, to find that we first need to find x = -2 in the horizontal axis.
f(-2) = 4
Now we want to find the value of x such that:
f(x) = 2
so now we need to find 2 in the vertical axis. we can see that the function is equal to 2 for x = -1.3 (approximation).
Learn more about functions:
https://brainly.com/question/1719822
#SPJ1
Landon analyzed data and found that the correlation coefficient for their line of best fit was -0.85. Marco analyzed a different set of data and found a correlation coefficient of 0.85. Marco states that since 0.85 is greater than -0.85, his data points have a better line of best fit than Landon. Is Marco correct? Why, or why not?
Answers
Marco's data points have a better line of best fit based on a comparison of Correlation coefficients.
Marco is incorrect in stating that his data points have a better line of best fit than Landon based solely on the comparison of correlation coefficients. The magnitude of the correlation coefficient alone does not determine the quality or strength of the line of best fit.
The correlation coefficient measures the strength and direction of the linear relationship between two variables. It ranges from -1 to +1. A positive correlation coefficient (such as 0.85) indicates a positive linear relationship, while a negative correlation coefficient (such as -0.85) indicates a negative linear relationship. The closer the correlation coefficient is to -1 or +1, the stronger the relationship. A correlation coefficient of 0 indicates no linear relationship.
In the case of Landon and Marco, both correlation coefficients have the same absolute value of 0.85, suggesting a strong linear relationship. However, the negative sign for Landon's correlation coefficient indicates a negative linear relationship, while the positive sign for Marco's correlation coefficient indicates a positive linear relationship.
The comparison between -0.85 and 0.85 should not be made in terms of greater or lesser quality of the line of best fit. The choice of a positive or negative correlation depends on the context and nature of the variables being analyzed.
The appropriateness of the line of best fit and the goodness-of-fit of the model should be evaluated based on additional factors such as the data points' distribution around the line, residuals, and the overall context of the analysis. These aspects provide more comprehensive insights into the quality of the fit and the reliability of the relationship being represented.
Therefore, Marco's data points have a better line of best fit solely based on a comparison of correlation coefficients. The interpretation of the correlation coefficient requires considering the nature of the variables and other factors influencing the analysis.
To know more about Correlation coefficients.
https://brainly.com/question/30634313
#SPJ11
ײ + 5× - 11 + 3ײ - 11 × + 2
hello guys please solve and give a solution tthankyou
Answers
Step-by-step explanation:
start by collecting like terms
4x² - 6x -9
use quadratic equation, a=4, b= 6 and 9 = c.
x = 5,78 or x = -4,28
I NEED HELP ASAP Which equation is equivalent to: −10r−6=115
A. 10r=−115+6
B. −10r=115+6
C. −10r=115−6
D. 10r=115−6
Answers
-10r=-115+6
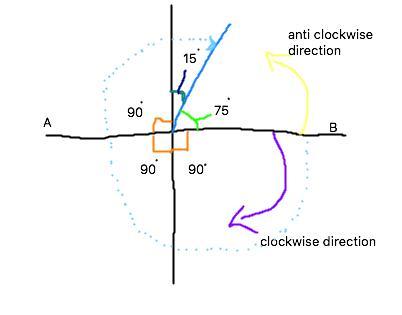
what negative angle is equivalent to a 75 angle
Answers
Answer: it’s actually -285
Step-by-step explanation: took test
The negative angle equivalent to a 75 angle is -285 angle.
We are given a 75 angle and we need to find a negative angle that is equivalent to the 75 angle.
What is a negative angle?A negative angle is defined as an angle generated in a clockwise direction from its given base.
We have a 75 angle which is in an anti-clockwise direction from the base AB as shown in the figure.
Now we will draw an angle in a clockwise direction from the base AB such that the angle reaches angle 75 which means it is equivalent to angle 75
We have,
Adding the angle from base AB till angle 75.
90° + 90° + 90° + 15° = 285°
Since the angle is measured in a clockwise direction we have,
285° = - 285°
The negative angle equivalent to a 75 angle is -285 angle.
Learn more about negative angles here:
https://brainly.com/question/11859743
#SPJ2
50.3 - 5.6 ÷ 0.7 × 1.6 of 3.5
Answers
Answer:
5.5 is the correct answer:)
Step-by-step explanation:
Hope this helped!!!
Please helpppp. Find the value of B in the rhombus

Answers
Answer:
18
Step-by-step explanation:
Angle AEB is a 90 angle
90 = 5b
18 = b
Use the Chain Rule to evaluate the partial derivatives∂u∂fand∂v∂fat(u,v)=(−2,−2).f(x,y,z)=x3+yz2,x=u2+v,y=u+v2,z=4uv(Give exact answers. Use symbolic notation and fractions where needed.)∂u∂f(u,v)=(−2,−2)Incorrect∂v∂f(u,v)=(−2,−2)=
Answers
The value of ∂u∂f(u,v)=(−2,−2) = -20 and ∂v∂f(u,v)=(−2,−2) = -45.
To evaluate the partial derivatives ∂u∂f(u,v)=(−2,−2) and ∂v∂f(u,v)=(−2,−2), we can use the Chain Rule. We first take the partial derivatives of f(x,y,z) with respect to x, y, and z, and then substitute in x = u2 + v, y = u + v2, and z = 4uv.
First, ∂f∂x=3x2, ∂f∂y=yz and ∂f∂z=y2.
Substituting in x = u2 + v, y = u + v2, and z = 4uv gives us: ∂f∂x=3(u2 + v)2, ∂f∂y=(u + v2)(4uv) and ∂f∂z=(u + v2)2.
Next, we use the Chain Rule to find ∂u∂f(u,v)=(−2,−2) and ∂v∂f(u,v)=(−2,−2):
∂u∂f(u,v)=(−2,−2)= ∂f∂x•∂x∂u + ∂f∂y•∂y∂u + ∂f∂z•∂z∂u = 3(u2 + v)2•(2u) + (u + v2)(4uv)•(1) + (u + v2)2•(4v) = 6u2 + 8uv + 4uv + 4v2 = 10uv + 6u2 + 4v2
∂v∂f(u,v)=(−2,−2)= ∂f∂x•∂x∂v + ∂f∂y•∂y∂v + ∂f∂z•∂z∂v = 3(u2 + v)2•(1) + (u + v2)(4uv)•(2v) + (u + v2)2•(4u) = 3 + 8uv + 8u2 = 8u2 + 8uv + 3
When (u,v)=(−2,−2), we have ∂u∂f(u,v)=(−2,−2) = 10(-2)(-2) + 6(-2)2 + 4(-2)2 = 20 - 24 - 16 = -20 and ∂v∂f(u,v)=(−2,−2) = 8(-2)2 + 8(-2)(-2) + 3 = -32 - 16 + 3 = -45.
To know more about partial derivatives click on below link:
https://brainly.com/question/29652032#
#SPJ11
A traffic camera sits on top of a tower that has a height of 39 ft. The angles of depression of a car on a straight road at the same level as that of the base of the tower and on the same side of the tower are 31°. Calculate the the distance between the base of the poll and the car. Round to the nearest tenth of a foot. *
Answers
Answer:
48ft
Step-by-step explanation:
Distance of car A from the towerConsider ∆ACD tan25 = 50/AC AC = 50/tan25 = 50/0.4663 = 107.2 ft Distance of car B from the towerConsider ∆BCD tan40 = 50/BC AC = 50/tan40 = 50/0.8391 = 59.6 ftDistance from cars A and B AB = AC – BC = 107.2 – 59.6 = 48 ft The distance between the two cars is 48ftplease i need help finishing this last question or i might get in trouble.
Solve.
w−(−23)=1.06
Enter your answer as a fraction in simplest form in the box.
w =

Answers
59/150
How?
w= 59/150
59/150 and -2/3 have to have the same denominators.
So, what I did was, -2/3×50= -100/150.
(Process of a new equation)
59/150-(-100/150)
[The two - signs cross each other out, making it a + ]
59/150+100/150 <- New Equation
__________________________________
59/150+100/150= 159/150
159/150= 1 9/150
9÷150=0.06
1+0.06= 1.06
(PROOF ABOVE)

Answer
add 1.06 = 1 3/50 = 1 3/50 + (-2/3) = 59/150
Step-by-step explanation:
37x - Ꮞx^3 + 22x^4 + 11
Standard form
Answers
You want to put the HIGHEST DEGREE FIRST
for a positive integer $p$, define the positive integer $n$ to be $p$-safe if $n$ differs in absolute value by more than $2$ from all multiples of $p$. for example, the set of $10$-safe numbers is $\{ 3, 4, 5, 6, 7, 13, 14, 15, 16, 17, 23, \ldots\}$. find the number of positive integers less than or equal to $10,000$ which are simultaneously $7$-safe, $11$-safe, and $13$-safe.
Answers
The quantity of positive numbers smaller than or equal to \($10,000$\) is \($\fbox{958}$\).
We see that a number \($n$\) is \($p$\)-safe if and only if the leftovers from\($n\mod p$\) is greater than \($2$\) and less than \($p-2$\); thus, there are \($p-5$\) residues \($\mod p$\) that a \($p$\)-safe number can have. Therefore, a number \($n$\) satisfying the circumstances of the issue may \($2$\) different residues \($\mod 7$\), \($6$\) different residues \($\mod 11$\), and \($8$\) different residues \($\mod 13$\). According to the Chinese Remainder Theorem, for a number \($x$\) that is \($a$\) (mod b) \($c$\) (mod d) \($e$\) (mod f) has one solution if \($gcd(b,d,f)=1$\). For instance, in this instance, the number \($n$\) can be: \(3 (mod 7) 3 (mod 11) 7 (mod 13)\)so since \($gcd(7,11,13)=1$\), there is \(1\) solution for \(n\) for this case of residues of \($n$\). As a result, according to the Chinese Remainder Theorem, \($n$\) can have \($2\cdot 6 \cdot 8 = 96$\) different residues mod \($7 \cdot 11 \cdot 13 = 1001$\). Thus, there are \($960$\) values of \($n$\) satisfying the conditions in the range \($0 < n \le 10010$\). Nevertheless, we now have to eliminate all values bigger than \($10000$\) that satisfy the conditions. We can simply see by looking at residues that the only suitable values are \($10006$\) and \($10007$\), so there remain \($\fbox{958}$\) values satisfying the conditions of the problem.
Learn more about positive numbers here
https://brainly.com/question/25474679
#SPJ4
Find the area for this problem

Answers
Answer:
63 for the whole figure, for the different shaded regions it goes as follows, 17.5 for the white area and 45.5 for the grey area
Step-by-step explanation:
if my avg is a 96 and my final exam is a 75 which is 25% of my whole grade what will my final grade be
Answers
Step-by-step explanation:
That means the 96 is 75% of your grade
96 (.75) + 75 (.25) = 90.75 final grade
The areas of the squares adjacent to two sides of a right triangle are 32 units^2 2 squared and 32 units^2 Find the length, xxx, of the third side of the triangle.
Answers
Answer:
8 units
Step-by-step explanation:
If the area of the squares are 32 units^2, we have that:
Area = Side * Side
Side^2 = 32
Side = sqrt(32) = 5.657 units
So as the squares are adjacent to two sides of the triangle, we have that the triangle has two sides of 5.657 units
As it is a right triangle, we can use the Pythagoras' theorem:
c^2 = a^2 + b^2
c^2 = 5.657^2 + 5.657^2
c^2 = 64
c = 8 units
Answer:
its 8
Step-by-step explanation:
BEDMAS QUESTIONS
Solve the following.
Show your work.
Round you asnwers to the nearest hundredth

Answers
Using BODMAS, the solutions of the expressions are: (1) 9, (2)-12, (3) 0.27, and (4) 0.24
What is BODMAS?We should know that BODMAS is a mathematical approach which means
B=BracketO=OffD=DivisionM=MultiplicationA=Addition S=SubtractionIn each of the expressions, we must follow the approach
1) \(\frac{(6+3)^{2} }{3*9}\)
Simplifying this we have 9²/9=81/9
=9
2) \(\frac{3^{2} -6*2}{(12-8)/2^{2} *10}\)
Using BODMAS we have
(9-12)/4/40
-3÷1/9
⇒-3*4
=-12
(3) \(\frac{4.5+2*2.5^{2}-6 }{8*4+9}\)
Using BODMAS we have
(4.5+2*6.25-6)/32+9
⇒(4.5+12.5-6)/41
=11/41=0.27
4 (\(\frac{3.5+16-2.5^{2} }{10.5-6*11}\))
Using BODMAS we have
(3.5+16-6.25)/10.5-66
Simplifying
(13.25)/-55.5
=0.24
Therefore, the values when simplified are (1) 9, (2)-12, (3) 0.27, and (4) 0.24
Learn more about BODMAS on https://brainly.com/question/29626866
#SPJ1