Define proportional reasoning
Answers
Answer:
It is coming to a conclusion based on rational thinking, comparing quantities to values.
Related Questions
NO LINKS!! Find the 10 terms of the sequence.
a1 = x, d = 3x
a1=
a2=
a3=
a4=
a5=
a6=
a7=
a8=
a9=
a10=
Answers
Answer:
\(x, \; 4x, \; 7x, \; 10x, \; 13x, \; 16x, \; 19x, \; 22x, \; 25x, \; 28x, ...\)
Step-by-step explanation:
\(\boxed{\begin{minipage}{8 cm}\underline{General form of an arithmetic sequence}\\\\$a_n=a+(n-1)d$\\\\where:\\\phantom{ww}$\bullet$ $a_n$ is the nth term. \\ \phantom{ww}$\bullet$ $a$ is the first term.\\\phantom{ww}$\bullet$ $d$ is the common difference between terms.\\\phantom{ww}$\bullet$ $n$ is the position of the term.\\\end{minipage}}\)
Given:
a = xd = 3xSubstitute the given values of a and d into the formula to create an equation for the nth term:
\(\implies a_n=x+(n-1)3x\)
\(\implies a_n=x+3nx-3x\)
\(\implies a_n=3nx-2x\)
To find the first 10 terms of the given arithmetic sequence, substitute n = 1 through 10 into the equation.
\(\begin{aligned}\implies a_1&=3(1)x-2x\\&=3x-2x\\&=x\end{aligned}\)
\(\begin{aligned}\implies a_2&=3(2)x-2x\\&=6x-2x\\&=4x\end{aligned}\)
\(\begin{aligned}\implies a_3&=3(3)x-2x\\&=9x-2x\\&=7x\end{aligned}\)
\(\begin{aligned}\implies a_4&=3(4)x-2x\\&=12x-2x\\&=10x\end{aligned}\)
\(\begin{aligned}\implies a_5&=3(5)x-2x\\&=15x-2x\\&=13x\end{aligned}\)
\(\begin{aligned}\implies a_6&=3(6)x-2x\\&=18x-2x\\&=16x\end{aligned}\)
\(\begin{aligned}\implies a_7&=3(7)x-2x\\&=21x-2x\\&=19x\end{aligned}\)
\(\begin{aligned}\implies a_8&=3(8)x-2x\\&=24x-2x\\&=22x\end{aligned}\)
\(\begin{aligned}\implies a_9&=3(9)x-2x\\&=27x-2x\\&=25x\end{aligned}\)
\(\begin{aligned}\implies a_{10}&=3(10)x-2x\\&=30x-2x\\&=28x\end{aligned}\)
Therefore, the first 10 terms of the given arithmetic sequence are:
\(x, \; 4x, \; 7x, \; 10x, \; 13x, \; 16x, \; 19x, \; 22x, \; 25x, \; 28x, ...\)what is the name of the point where the sides of an angle intersect
Answers
Answer:
vertex
Step-by-step explanation:
The rays that form an angle intersect at the vertex of the angle.
If a person travels 440 meters in 11 seconds, what is the average speed of the person?
Answers
Step-by-step explanation:
speed=distance÷time
A.V.S=440÷11=40m/s
hope it helps.. Please mark brainliest.
Answer:
40 m/s
Step-by-step explanation:
Find:
We are asked to find the unit rate, How many meters per 1 second?
Know:
440 meters in 11 seconds
Solve:
440 meters in 11 seconds
? meters in 1 second
440/11 = 40 meters per second
Answer:
The average speed of the person is 40 m/s
Antonio expresses the term 121x^2 as a square with the side lengths of 11x. What is true about the term 121x^2 A. It can also be expressed using a rectangle B. It must be part of a perfect square trinomial C. It is a perfect squareD. It must be part of a difference of squares
Answers
If the term 121x^2 can be expressed as a square with side lengths of 11x, that means the term 121x^2 is a perfect square, since there is a expression that, when squared, is equal to 121x^2:
\((11x)^2=11x\cdot11x=121x^2\)Therefore the correct option is C.
Find the experimental probability that someone surveyed is between the ages of 35 and 62

Answers
hehehehehehehehehehehehehehehehehehehehe
Solve the given initial-value problem.
y''' − 2y'' + y' = 2 − 24ex + 40e5x, y(0) =
1
2
, y'(0) =
5
2
, y''(0) = −
11
2
the values for the first 3 derivatives derivatives of y are 1/2, 5/2, -11/2 respectively
Answers
The given differential equation:
y''' − 2y'' + y' = 2 − 24ex + 40e5x,
y(0) = 1/2, y'(0) = 5/2, y''(0) = −11/2
Therefore, the next solution is 13/2
Differential Equation:
In mathematics, a differential equation is an equation relating one or more unknown functions to their derivatives. In applications, functions usually represent physical quantities, derivatives represent rates of change, and differential equations define the relationship between them. These relationships are common.
Now,
Given differential equation is
y''' - 2y'' +y' = 2- 24eˣ +40e⁵ˣ ------------ (1)
Auxiliary equation is m³ - 2m² +2m = 0
Now,
m(m² - 2m +2) = 0
⇒ m(m-1)² = 0
Therefore, m = 0,1,1
Therefore,
\(y_{c} = c_{1}+ c_{2} e^{x} + c_{2}x e^{x}\)
Now, we have to find the particular solution by method of undetermined coefficient.
\(y'_{y} = a + b(x^{2} e^{x} +2xe^{x} ) +5ce^{x}\)
⇒ \(y''_{p} = a + bx^{2} e^{x} +2bxe^{x} +5ce^{x}\)
⇒ \(y''_{p} = b(x^{2} e^{x} +2xe^{x}) + 2b(ex^{x}+ e^{x} +25ce^{x}\)
⇒ \(y'''_{p} = bx^{2} e^{x} +6bxe^{x} +6be^{x} +125ce^{5x}\)
Putting these values in differential equation (1), we get:
y'''(0) = 13/2
Complete Question:
Solve the given initial-value problem. y''' ? 2y'' + y' = 2 ? 24ex + 40e5x, y(0) = 1 2 , y'(0) = 5/ 2 , y''(0) = ? 13/ 2
Learn more about Differential Equation:
https://brainly.com/question/16663279
#SPJ4
3/8+ 5/6 divided by 5
Answers
Answer:
Answer is 29/120 I think i worked it out so if it inst right truly im sorry but i belive this is the answer.
Answer:
= 13
24
Step-by-step explanation:
3 + 5 / 5
8 6
do the division first as per the law of operation of math requires.
5 / 5 = 5 x 1 = 1
6 6 5 6
3 + 1 = 9 + 4 = 13
8 6 24 24
i'll mark brainliest thanks
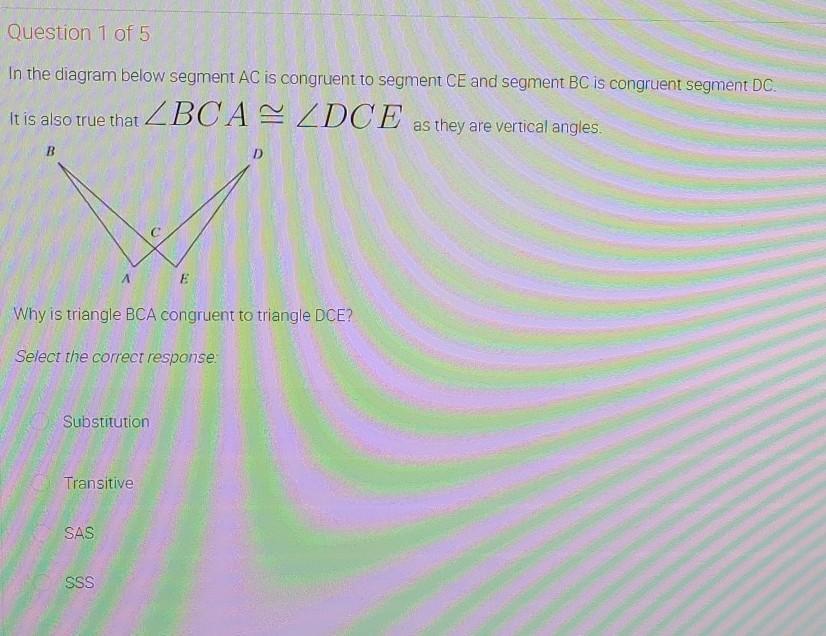
Answers
Answer:
Transitive
Step-by-step explanation:
A square garden has a length of (x+3) ft and a width of (x+2) ft. what is the perimeter and area of the garden?
Answers
Answer:
Perimeter:\(4x+10\) feet
Area:\(x^{2}+5x+6\) feet
Step-by-step explanation:
The perimeter is equal to 2*width +2*length. The width is x+2 and the length is x+3, therefore the perimeter is equal to 2x+4+2x+6 which equals 4x+10.
The area is equal to width*length
(x+3)(x+2)=\(x^{2}+2x+3x+6=x^{2}+5x+6\)
a rectangle with a width of 30 centimeters has a perimiter of 100 centimeters to 160 centimeters graph a compound inequality
Answers
Answer:
5 ≤ L ≤ 35
Step-by-step explanation:
Let w represent the width of the rectangle.
The perimeter (P) of the rectangle is given by:
P = 2w + 2L
Where L is the length of the rectangle.
We know that w = 30 cm and that the perimeter is between 100 and 160 cm. We can now set up our compound inequality:
100 ≤ 2(30) + 2L ≤ 160
100 ≤ 90 + 2L ≤ 160
10 ≤ 2L ≤ 70
We can now divide both sides by 2 to solve for L:
5 ≤ L ≤ 35
Therefore, the compound inequality that represents the graph of a rectangle with a width of 30 centimeters and a perimeter of 100 centimeters to 160 centimeters is: 5 ≤ L ≤ 35
factorise x³-4x²+x+6
Answers
The binomial factors of x³- 4x²+x+6 are (x+2), (x+3), and (x-1).
Using the splitting and grouping the terms:
x³ + 4x² + x - 6
= x³ + 2x² + 2x² + x - 6 [Splitting 4x² = 2x² + 2x²]
= (x³ + 2x²) + (2x² + x - 6)
= x² (x + 2) + (2x² + 4x - 3x - 6)
= x² (x + 2) + [ 2x (x + 2) - 3 (x + 2)]
= x² (x + 2) + (x + 2) (2x - 3)
= (x + 2) ( x² + 2x - 3)
= (x + 2) ( x² + 3x - x - 3)
= (x + 2) [x (x + 3) - 1 (x + 3)]
= (x + 2) (x + 3) (x - 1)
Hence, the binomial factors are (x + 2), (x + 3) and (x - 1)
To learn more about factorise here,
https://brainly.com/question/10718512
https://brainly.com/question/24734894
The hanger image below represents a balanced equation.
Select an equation that represents the image.
Choose 1 answer:
Choose 1 answer:
(Choice A)
A
5m=505m=505, m, equals, 50
(Choice B)
B
\dfrac{m}{5}=50
5
m
=50start fraction, m, divided by, 5, end fraction, equals, 50
Find the value of mmm that makes the equation true.
m=m=m, equals
Answers
Answer:
The answer is A
Step-by-step explanation:
5m=505m=505,m equal, 50
what is f(3) for f(x) = 3x + 2
Answers
Answer:
11
Step-by-step explanation:
f(x) = 3x + 2
Let x = 3
f(3) = 3*3 +2
f(3) = 9+2
= 11
Answer:
f(3) = 11Step-by-step explanation:
f(x) = 3x + 2
In order to find f(3) substitute the value of x that's 3 into f (x) that's replace every x in f (x) by 3
That's
f(3) = 3(3) + 2
= 9 + 2
We have the final answer as
f(3) = 11Hope this helps you
Brianna needs to contact members of the softball league. She calls 2 members of the softball league. Those 2 people each call 2 more people in the afternoon. That evening, those additional people each call 2 others. How many people are called that evening?
Answers
Answer:
8
Step-by-step explanation:
because I plus all 2 and say evening how many see
Plz help I’ll mark you

Answers
Answer:
option (B) is the answer
2ˣ² ⁻⁵ˣ⁻⁴<4
log₀.₃(x²+3)≥ log₀.₃(4 x)

Answers
The solutions to the inequalities are given as follows:
\(2^{x^2 - 5x - 4} < 4\): 2 < x < 3.\(\log_{0.3}{(x^2 + 3)} \geq \log_{0.3}{4x}\): x ≤ 1 or x ≥ 3.How to solve the inequalities?The first inequality is given as follows:
\(2^{x^2 - 5x - 4} < 4\)
We have that 4 = 2², hence:
\(2^{x^2 - 5x - 4} < 2^2\)
As the exponential function is increasing over it's entire domain, the inequality can be represented as follows:
x² - 5x - 4 < 2
x² - 5x - 6 < 0.
The quadratic equation x² - 5x - 6 is concave up, hence it's negative between it's roots, obtained as follows:
(x - 2)(x - 3) = 0.
Applying the Factor Theorem:
x - 2 = 0 -> x = 2.x - 3 = 0 -> x = 3.Hence the solution to the inequality is of:
2 < x < 3.
The second inequality is given as follows:
\(\log_{0.3}{(x^2 + 3)} \geq \log_{0.3}{4x}\)
The logarithm function is also increasing over it's entire domain, hence the inequality is simplified as follows:
x² + 3 ≥ 4x
x² - 4x + 3 ≥ 0.
Another concave up quadratic equation, which is non-negative to the left of the smallest root and to the right of the highest root.
The roots are obtained by factoring as follows:>
(x - 3)(x - 1) = 0.
Hence:
x - 3 = 0 -> x = 3.x - 1 = 0 -> x = 1.Then the solution is given as follows:
x ≤ 1 or x ≥ 3.
More can be learned about inequalities at https://brainly.com/question/25275758
#SPJ1
Solve 3(2-4x)=5-8x
PLS SHOW CLEAR ALGEBRAIC WORKING
Answers
The solution to the given algebraic expression 3(2-4x) = 5-8x is x = 1/4
How to solve algebraic expression?3(2-4x) = 5-8x
open parenthesis
6 - 12x = 5 - 8x
combine like terms
6 - 5 = -8x + 12x
1 = 4x
divide both sides by 4
x = 1/4
Ultimately, x = 1/4 is the answer to the algebraic expression.
Read more on algebra:
https://brainly.com/question/4541471
#SPJ1
Use the table in the following problem.
Which industry had the greatest percentage increase in profits as a percentage of sales between 1966 and 1974?
-Chemicals
-Petroleum
-Drugs
What was the percentage increase (to the nearest tenth)?
-13.4%
-11.8%

Answers
Answer:Petroleum = 15.32%
Drugs = 12.9%
Chemicals = 2.5%
Motor Vehicles = -56.5% (Negative)
Electrical = -18.8% (Negative)
Food = 3.7%
Step-by-step explanation:
Help pls George is building a fence around a rectangular dog run. He is using his house as one side of the run. The area of the dog run will be 240 square feet. The length of the run is 30 feet, and the width is (30 minus x) feet. The diagram below shows his plan.
Recall the formulas for area and perimeter: A = lw and P = 2l + 2w.
Answers
The width of the dog run is 20 feet.
In the given problem, the length of the dog run is given as 30 feet.
The area of the dog run is also given as 240 square feet.
Using the formula for the area of a rectangle (A = lw), we can solve for the width (w).
Rearranging the formula, we have w = A / l.
Plugging in the values, we get w = 240 / 30 = 8 feet.
Since the width is given as (30 minus x) feet, we can set up an equation:
30 - x = 8. Solving for x, we find x = 22.
Therefore, the width of the dog run is 20 feet (30 - 22 = 8).
In this problem, the length and width of the dog run are defined by the dimensions of the fence being built around it.
The area of the dog run is given as 240 square feet.
By using the formula for the area of a rectangle, we can solve for the width. We are also given that the length is 30 feet.
Setting up an equation with the given width (30 minus x) and solving for x, we find that x is equal to 22.
This means that the width of the dog run is 8 feet. The main answer to the problem is that the width of the dog run is 20 feet (30 - 22 = 8).
for such more questions on width
https://brainly.com/question/28107004
#SPJ8
Given points P, Q, R, and S, decide whether PQ and RS are parallel, perpendicular, or neither.
P (9,10) Q(10,3) R (-9,4) S (-2,5)
Answers
Answer:
Opposite Sides of Parallelogram are equal
If All opposite sides are equal , it is Parallelogram
For this You need to use distance formula that is
√(x2-x1)2+(y2-y1) 2
what is the probability that either event will occur? ASAP

Answers
The probability that either event will occur is 0.67
What is the probability that either event will occur?From the question, we have the following parameters that can be used in our computation:
Event A = 3
Event B = 1
Other Events = 2
Using the above as a guide, we have the following:
Total = A + B + C
So, we have
Total = 3 + 1 + 2
Evaluate
Total = 6
So, we have
P(A) = 3/6
P(B) = 1/6
For either events, we have
P(A or B) = 3/6 + 1/6 = 0.67
Hence, the probability that either event will occur is 0.67
Read more about probability at
brainly.com/question/251701
#SPJ1
3.1 Which basic property of operations was used in each of the following
calculations?
3.1.1 25 x 4 = 4 x 25 = 100
3.1.2 412 412 412 + (-412) = 0
3.1.3 25 +37
-
=
= 20 + 5+ 30+7
= 20 +30 +5+7
= 50+ 12 = 62
Answers
3.1.1 The basic property of operations used is the commutative property of multiplication.
3.1.2 The basic property of operations used is the additive inverse property.
3.1.3 The basic property of operations used is the associative property of addition.
3.1.1 The basic property of operations used in this calculation is the commutative property of multiplication. It states that the order of the factors in a multiplication problem can be rearranged without changing the product. In this case, the numbers 25 and 4 were swapped, resulting in the same product of 100.
3.1.2 The basic property of operations used in this calculation is the additive inverse property. It states that for any number, there exists an additive inverse such that when the number and its additive inverse are added together, the result is zero. In this case, adding 412 and its additive inverse (-412) results in zero.
3.1.3 The basic property of operations used in this calculation is the associative property of addition. It states that the grouping of numbers being added does not affect the sum. In this case, the numbers 25, 37, 20, 5, 30, and 7 were regrouped to facilitate easier mental addition. By grouping 25 and 37, and then grouping 20, 5, 30, and 7, the final sum of 62 is obtained, which is the same as adding all the numbers together in the original order.
for such more question on commutative property
https://brainly.com/question/2475734
#SPJ8
A client would like this logo printed onto a canvas that is at least 70 inches tall. The original logo is 4.5 inches wide by 3.6 inches tall. Which of the following dimensions will keep the logo in proportion and large enough to meet the clients requirements?
Answers
Answer:
87.5 by 70 inches
Step-by-step explanation:
No options were given. So, I will calculate the minimum width
Given
\(Original\ Logo = 4.5 : 3.6\)
Height = 70 in ---- of the printed logo
Required
Determine the dimension that keeps the requirement
Let x be the width of the printed logo.
So, the ratio can be represented as:
\(Printed\ Logo = x : 70\)
Equate both ratios
\(x : 70 = 4.5 : 3.6\)
As fraction
\(x / 70 = 4.5 / 3.6\)
Multiply through by 70
\(70 * x / 70 = 4.5 / 3.6* 70\)
\(x = 87.5\)
So, one of the dimension that meets the requirement is a width of 87.5 inches
In parallelogram EFGH, MLH =
F
Зу
(3x - 15)°
2(y + 1)
H
(7x- 5)°
y + 8
o and HG
=

Answers
The measure of HG is 12
What is a parallelogram?A parallelogram is a quadrilateral with opposite sides parallel (and therefore opposite angles equal). A quadrilateral with equal sides is called a rhombus, and a parallelogram whose angles are all right angles is called a rectangle.
The opposite sides of a parallelogram are equal. This means that 3y = y+8
3y = y+8
3y-y = 8
2y = 8
divide both sides by 2
y = 8/2
y = 4
if y = 4 and HG is y+8
therefore
the measure of HG = 4+8
= 12
learn more about parallelogram from
https://brainly.com/question/970600
#SPJ1
A community would like to add a brick paver border around their swimming pool. They created the following image to represent the pool with the border. A large rectangle with a length of 48 feet and a width of 28 feet. Inside of it is another rectangle with a length of 32 feet and a width of 12 feet. Part A: Find the total area of the brick paver border that surrounds the 12 ft by 32 ft pool. Show your work. (2 points) Part B: If brick pavers cost $8 per square foot, what is the total cost of the brick pavers needed for this project? Explain. (2 points)
Answers
Part A: The total area of the brick paver border is \(960\) square feet.
Part B: The total cost of the brick pavers needed for this project is $\(7,680\).
Part A: To find the total area of the brick paver border, we need to subtract the area of the pool from the area of the larger rectangle. The area of the pool is \(32\) feet multiplied by 12 feet, which is equal to \(384\)square feet.
The area of the larger rectangle is \(48\) feet multiplied by \(28\) feet, which is equal to \(1,344\) square feet. Therefore, the area of the brick paver border is \(1,344\) square feet minus \(384\) square feet, which equals \(960\) square feet.
Part B: If brick pavers cost $\(8\)per square foot, we can calculate the total cost by multiplying the cost per square foot by the total area of the brick paver border. The total area of the brick paver border is \(960\) square feet, and the cost per square foot is $\(8\).
Therefore, the total cost of the brick pavers needed for this project is $\(8\)multiplied by \(960\) square feet, which equals $\(7,680\).
Note: The calculations provided assume that the border consists of a single layer of brick pavers.
For more such questions on area:
https://brainly.com/question/2607596
#SPJ8
Can you help me please?

Answers
Answer:
53/54 = 106/108
Step-by-step explanation:
You can find the answer because 53/54 * 2/2 = 106/108
2/2 = 1 - right? When you multiply any number by one, it stays the same. That's how you can tell, 53/54 = 106/108.
Answer:
No it cant
Step-by-step explanation:
it would have to be 54/54 to be equal to 1.
What is the square root of -1?
Answers
......................
Which of the following shapes have an area of 48 square feet? Select all that apply.
A scalene triangle with a base of 8 feet and a height of 6 feet.
A right triangle with a base of 9 feet and a height of 10 2/3 feet.
A rectangle with a base of 19.2 feet and a height of 2.5 feet.
A parallelogram with a base of 16 feet and a height of 3 feet.
Answers
The area of a triangle is (b•h)/2
And the area of a rectangle and parallelogram would just be b•h
1) 8(6) = 48/2 =24
2) 9(10 2/3) = 96/2 =48
3) 19.2(2.5) = 48
4) 16(3) = 48
Hope this is right and hope it helps. Have a good day
Jaime borrowed $2 from Alba. Jaime realized that Alba had previously borrowed $10 from him and asked her to return it back so he could buy a soccer ball that costs $12. Alba is happy to pay him the money back but tells Jaime that even if she paid him back right now, he will be short $4 from buying the ball.
Who is correct, Jaime and or Alba? Please use a number sentence (like 1 + 1 = 2 or -1 + -1 = -2) as part of your evidence
Answers
Answer:
Jaime
Step-by-step explanation:
Assuming he keeps the money he just borrowed
---} 2+10= $12
But if she requests her money back then she will be correct
---} -2+10= $8
Find the missing angles.
with solution

Answers
Hello!
y = 88° (opposite are equal)
z = 180° - 128° = 52° (straight angle = 180°)
x = 180° - 140° = 40° (straight angle = 180°)
Answer:
x=40°
y=88°
z=52°
Step-by-step explanation:
Solution Given:
x+140°=180°
Since the sum of the angle of a linear pair or straight line is 180°.
solving for x.
x=180°-140°
x=40°
\(\hrulefill\)
y°=88°
Since the vertically opposite angle is equal.
therefore, y=88°
\(\hrulefill\)
z+128°=180°
Since the sum of the angle of a linear pair or straight line is 180°.
solving for z.
z=180°-128°
z=52°