Convert 2 3/4 to a decimal number.
Answers
Answer:
2.75
Step-by-step explanation:
3/4 is .75 in decimal
Related Questions
is james scored a 40 on a test with a mean of 38 and the standard deviation was for whataburger z-score be
Answers
The value of z-score for James is 0.2
Step-by-step explanation:
From the formula of z-score we know that
z-score = individual score - mean / standard deviation
Given
James score = 40
Mean = 38
Standard deviation = 10 (missing in question)
To find
z-score =?
Let's put the values in the formula
z-score = 40-38/ 10
z-score = 0.2
You can learn more about z-score from
https://brainly.com/question/25638875
#SPJ4
Someone help me it’s timed !!

Answers
Answer:
Alternative exterior angles --> <1 and <7
Corresponding angles --> <2 and <6
Alternative Interior angles --> <3 and <5
Hope this helps and stay safe, happy, and healthy, thank you :) !!
Use the Laws of logarithms to rewrite the expression in a form with no logarithm of a product, quotient or power. After rewriting we have with the constant A = the constant B and the constant C = In x
Answers
The expression \(ln \sqrt[3]{\frac{A^2B}{C}}\) is equivalent to \(ln(\frac{B}{lnx})\).
The expression in a form with no logarithm of a product, quotient or power is;
\(ln \sqrt[3]{\frac{A^2B}{C}}\)
Using the laws of logarithms, we have;
\(\ln \sqrt[3]{\frac{A^2B}{C}} = \frac{1}{3}\ln(A^2B)-\ln(C)\)
Substituting A = B and C = ln x, we get;
\(\frac{1}{3}\ln(A^2B)-\ln(C) = \frac{1}{3}\ln(B^3)-\ln(lnx) = \ln(\sqrt[3]{B^3})-\ln(lnx) = \boxed{\ln(\frac{B}{lnx})}\)
Therefore, the expression \(ln \sqrt[3]{\frac{A^2B}{C}}\) is equivalent to \(ln(\frac{B}{lnx})\).
Know more about the expression here:
https://brainly.com/question/1859113
#SPJ11
Use the substitution method to show that for the recurrence equation:
T( 1 )=1
T( n )=T( n/2 ) + n
the solution is T( n )=O ( n )
Answers
The substitution method proved that the solution to the recurrence equation T(n) = T(n/2) + n is T(n)
To show that the solution to the recurrence equation T(n) = T(n/2) + n is T(n) = O(n) using the substitution method, to prove that T(n) is upper-bounded by a linear function of n.
We will use the substitution method to prove this by assuming that T(n) ≤ c × n for some constant c and for all n that are powers of 2.
Base case: Let's consider n = 1. The base case is given as T(1) = 1, which satisfies the inequality T(1) ≤ c × 1, where c can be chosen as any positive constant.
Inductive hypothesis: Assume that for all k < n, the inequality T(k) ≤ c × k holds.
Inductive step: We need to prove that T(n) ≤ c × n.
Using the recurrence equation, we have:
T(n) = T(n/2) + n
By the inductive hypothesis, we can substitute T(n/2) with c × (n/2):
T(n) ≤ c × (n/2) + n
Simplifying:
T(n) ≤ (c/2) × n + n
T(n) ≤ (c/2 + 1) × n
Let's choose c = 2 to ensure (c/2 + 1) = 2, resulting in:
T(n) ≤ 2 × n
Therefore, we have shown that T(n) is upper-bounded by a linear function of n, specifically T(n) = O(n).
To know more about equation here
https://brainly.com/question/29657983
#SPJ4
1) There are 8 college basketball teams in a certain
Sub-Division
How many ways are there to choose 6 teams for the playoffs?
Answers
There are 28 ways to choose 6 teams for the playoffs if there are 8 college basketball teams in a certain sub-division.
To determine the number of ways to choose 6 teams for the playoffs out of the 8 college basketball teams in a certain Sub-Division, we can use the combination formula. The formula for combinations is given by
nCr = n! / (r! * (n-r)!),
where n represents the total number of teams and r represents the number of teams to be chosen.
In this case, n = 8 and r = 6.
Plugging in these values, we have
8C6 = 8! / (6! * (8-6)!) = 8! / (6! * 2!) = (8 * 7) / (2 * 1) = 28.
Therefore, there are total 28 ways to choose 6 teams.
To know more about ways refer here:
https://brainly.com/question/4318885
#SPJ11
Trey's Coffee Shop makes a blend that is a mixture of two types of coffee. Type A coffee costs Trey $5.80 per pound, and type B coffee costs $4.25 per pound. This month, Trey made 142 pounds of the blend, for a total cost of $724.40. How many pounds of type A coffee did he use?
Answers
Using a system of equations, the quantity of Type A coffee that Trey's Coffee Shop blended with Type B coffee was 78 pounds.
What is a system of equations?A system of equations or simultaneous equations is two or more equations solved concurrently, simultaneously, or at the same time.
Unit Cost Per Pound:
Type A coffee = $5.80
Type B coffee = $4.25
The total quantity of pounds of the blend = 142 pounds
The total cost of 142 pounds = $724.40
Let the number of Type A coffee = x
Let the number of Type B coffee = y
Equations:x + y = 142 ... Equation 1
5.8x + 4.25y = 724.40 ... Equation 2
Multiply Equation 1 by 4.25:
4.25x + 4.25y = 603.5 ... Equation 3
Subtract Equation 3 from Equation 2:
5.8x + 4.25y = 724.40
-
4.25x + 4.25y = 603.5
1.55x = 120.9
x = 78
Substitute x = 78 in either equation:
x + y = 142
78 + y = 142
y = 64
Thus, 78 pounds of Type A coffee was used for the mixture.
Learn more about a system of equations at https://brainly.com/question/13729904.
#SPJ1
Use the following lines to answer the question. line g: y=−45x+75 line h: y=54x+34 Is line g perpendicular to line h? Why or why not? No, because the slopes of lines g and h have different signs. Yes, because the slopes of lines g and h are opposite and reciprocal. Yes, because the slopes of lines g and h are opposite and the y-intercepts are different. No, because the y-intercepts of lines g and h are different.

Answers
Answer:
No, because the y-intercepts of lines g and h are different.
Step-by-step explanation:
HELP I GOTTA TURN THIS IN QUICK

Answers
Answer:
(0, 0), (4, 0), (4, -5)
Step-by-step explanation:
This one keeps the same lengths of the previous triangle. It also keeps the same proportions (or something) etc, etc. I solved this problem by graphing and seeing which one fit best.
the niagara falls incline railway has an angle of elevation of 30° and a total length of 196 feet. how many feet does the niagara falls incline railway rise vertically? ..... feet
Answers
The Niagara Falls incline railway rises vertically by approximately 98 feet.
The angle of elevation of 30° indicates the angle between the incline railway and the horizontal ground. The total length of the incline railway is given as 196 feet.
To find the vertical rise, we can use trigonometry. The vertical rise can be determined by calculating the sine of the angle of elevation and multiplying it by the total length of the incline railway:
Vertical rise = Total length × sine(angle of elevation)
Vertical rise = 196 ft × sin(30°)
Vertical rise ≈ 196 ft × 0.5
Vertical rise ≈ 98 ft
Therefore, the Niagara Falls incline railway rises vertically by approximately 98 feet.
You can learn more about Niagara Falls at
https://brainly.com/question/12736955
#SPJ11
In 2010, the population of a city was 167,000. From 2010 to 2015, the population grew by 8%. From 2015 to 2020, it fell by 3%. How much did the population decrease from 2015 to 2020, to the nearest 100 people?
Answers
The population decreased by 5,400 people from 2015 to 2020.
By how much did the population decrease?Also known as population decline, means the reduction in a human population size
Population in 2015 = Population in 2010 + Growth from 2010 to 2015
Population in 2015 = 167,000 + (8% of 167,000)
Population in 2015 = 167,000 + 13,360
Population in 2015 = 180,360
Population in 2020 = Population in 2015 - Decrease from 2015 to 2020
Population in 2020 = 180,360 - (3% of 180,360)
Population in 2020 = 180,360 - 5,411.8
Population in 2020 = 174,948.2
The population decrease from 2015 to 2020 is:
= Population in 2015 - Population in 2020
= 180,360 - 174,948.2
= 5,411.8
= 5,400 to nearest 100 people.
Read more about population
brainly.com/question/29885712
#SPJ1
the waiting time at an elevator is uniformly distributed between 30 and 200 seconds. find the mean and standard deviation of the waiting time.
Answers
49.07 is the mean and standard deviation of the waiting time .
What is standard deviation in math?
Your dataset's average level of variability is represented by the standard deviation. It reveals, on average, how far away from the mean each value is.
A low standard deviation means that values are clustered close to the mean, whereas a high standard deviation means that values are typically far from the mean.
Let X shows the waiting time. So mean
μ = E(x) = a + b/2 = 30 + 200/2 = 115
Standard deviaiton
σ = \(\sqrt{\frac{(b - a )^{2} }{12} }\)
= \(\sqrt{\frac{(200 -30)^{2} }{12} }\)
= 49.07
Learn more about standard deviation
brainly.com/question/16555520
#SPJ4
In this figure, AB∥CD and m∠6=75° . What is m∠3 ?
115°
75°
15°
105°
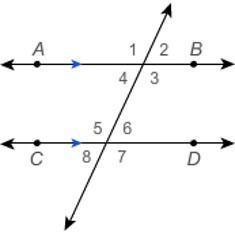
Answers
The measure of angle <3 is 105 degrees
How to use the diagram to find the measure of angle 3?The diagram that completes the question is added as an attachment
The angle is given as
<6 = 75
From the diagram, we have
<3 + <6 = 180 degrees
The above is true by the sum of internal angles between parallel lines
So, we have
<3 + 75 = 180
Subtract 75 from both sides of the equation
So, we have
<3 + 75 - 75 = 180 - 75
Evaluate the like terms
So, we have
<3 = 105
Hence, the measure of angle <3 is 105 degrees
Read more about angles at
brainly.com/question/7620723
#SPJ1
The sum of two numbers is 10. The larger number is 4
times the smaller number. What are the two numbers?
Original system: x + y = 10,
y = 4x
Slope-intercept form:
y = -x + 10
y = 4x
Answers
Answer:
x=8 and y=2
Step-by-step explanation:
x+y=10
x=4y
x+y=10
4y+y=10
5y=10(divide both sides by 5)
y=2
x=4y=4*2=8
Answer:
2 and 8.
Step-by-step explanation:
y = -x + 10
y = 4x
If we subtract we eliminate y:
0 = -x + 10 - 4x
0 = -5x + 10
5x = 10
x = 2.
and y = 4 * 2 = 8.
find the average value of f over the given rectangle. f(x, y) = 5ey x + ey , r = [0, 6] ⨯ [0, 1]
Answers
The average value of f over the rectangle [0,6] x [0,1] is approximately 3.427.
The average value of a function f over a rectangle R is given by:
avg(f) = (1/Area(R)) * double integral of f over R
Here, f(x,y) = 5e^(yx) + e^y and R = [0,6] x [0,1]
The area of R is given by:
Area(R) = (6 - 0) * (1 - 0) = 6
So, the average value of f over R is:
avg(f) = (1/6) * double integral of f over R
We can evaluate the double integral using iterated integration. First, we integrate f with respect to y from 0 to 1, and then integrate the result with respect to x from 0 to 6:
integral of f(x,y) dy = integral of (5e^(yx) + e^y) dy
= (5x/2)e^(yx) + e^y + C
where C is the constant of integration.
Now, we integrate this result with respect to x from 0 to 6:
integral of [(5x/2)e^(yx) + e^y] dx = [(5/2) * integral of xe^(yx) dx] + integral of e^y dx
= [(5/2) * (1/y)e^(yx) - (5/2)(1/y^2)(e^(yx) - 1)] + ey + C
where C is another constant of integration.
Therefore, the average value of f over R is:
avg(f) = (1/6) * [(5/2) * (1/y)e^(yx) - (5/2)(1/y^2)(e^(yx) - 1) + ey] evaluated from y=0 to y=1 and x=0 to x=6
avg(f) = (1/6) * [(5/2) * (1/e^6 - 1) - (5/2)(1/e - 1/e^6) + e - 1]
avg(f) = (1/6) * [(5/2) * (1 - e^-6) - (5/2)(e^-1 - e^-6) + e - 1]
avg(f) = (1/6) * [(5/2) * (1 - e^-6 - e^-1 + e^-6) + e - 1]
avg(f) = (1/6) * [(5/2) * (1 - e^-1) + e - 1]
avg(f) ≈ 3.427
Therefore, the average value of f over the rectangle [0,6] x [0,1] is approximately 3.427.
Learn more about average value here
https://brainly.com/question/30031427
#SPJ11
FILL THE BLANK.Two rays with a common end point form an _____
Answers
Two rays with a common endpoint form an angle. An angle is defined as a geometric figure formed by two rays that share a common endpoint. In other words, an angle is formed when two rays emanating from a common point, and this common point is known as the vertex.
The rays are the sides of the angle, and the angle is measured in degrees. Angles have different measures, ranging from 0 degrees to 360 degrees. The two rays that make up an angle are also called the sides or arms of the angle. The angle is measured in degrees, and the size of the angle depends on the distance between the two sides of the angle that meet at the vertex.
In geometry, an angle can be named in different ways, depending on the context in which it is being used. Angles are essential in mathematics, physics, and other scientific fields, where they are used to measure the rotation of an object, determine the direction of an object, and in other applications involving rays and lines. Two rays with a common endpoint form an angle.
Learn more about rays from the given link
https://brainly.com/question/13144568
#SPJ11
david has d books, which is 3 times as many as jeff and i as many as paula. how many books do the three of them have altogether, in terms of d?
Answers
David, Jeff, and Paula have (7d)/3 books.
To find out how many books David, Jeff, and Paula have altogether in terms of d, we can use the given information as follows:
1. David has d books.
2. David has 3 times as many books as Jeff, so Jeff has d/3 books.
3. David has the same number of books as Paula, so Paula also has d books.
Now, to find the total number of books for all three of them, we simply add the number of books each person has:
Total books = David's books + Jeff's books + Paula's books
Total books = d + d/3 + d
To combine these terms, we can find a common denominator (in this case, 3):
Total books = (3d + d + 3d) / 3
Now, we can simplify the expression:
Total books = (7d) / 3
So, altogether, David, Jeff, and Paula have (7d)/3 books in terms of d.
Learn more about denominator:
https://brainly.com/question/19249494
#SPJ11
Find an equation of the plane through the given point and parallel to the given plane. origin 3x - y + 3z = 4
Answers
An equation of the plane through the origin and parallel to the plane 3x - y + 3z = 4 is 3x - y + 3z = 0.
To find an equation of the plane through the origin and parallel to the plane 3x - y + 3z = 4, we can use the fact that parallel planes have the same normal vector.
Step 1: Find the normal vector of the given plane.
The normal vector of a plane with equation Ax + By + Cz = D is . So, in this case, the normal vector of the given plane is <3, -1, 3>.
Step 2: Use the normal vector to find the equation of the parallel plane.
Since the parallel plane has the same normal vector, the equation of the parallel plane passing through the origin is of the form 3x - y + 3z = 0.
Therefore, an equation of the plane through the origin and parallel to the plane 3x - y + 3z = 4 is 3x - y + 3z = 0.
To know more about equation refer here:
https://brainly.com/question/21511618
#SPJ11
HELP PLEASE IM SO CONFUSED
Theater Club Stage Crew
The school's theater club is building sets that will make ordinary students look like giants. The actors need a door, a table, and a stool that will make them look almost twice as tall!
DOOR: actual height is 80 inches and Height on Set is 44 inches
TABLE: actual height is 28 inches
STOOL: actual height is 18 inches
The heights of the objects in the set are proportional to the actual heights of objects. What is the CONSTANT OF PROPORTIONALITY? Write as a whole number, decimal or fraction
Answers
The constant of proportionality of the relation between the height on set and the actual height is given as follows:
0.55.
What is a proportional relationship?A proportional relationship is defined according to the equation presented as follows:
y = kx.
In which k is the constant of proportionality, representing the increase in the output variable y when the constant variable x is increased by one.
The variables for this problem are given as follows:
y is the height on set.x is the actual height.Considering the values of these variables for the door, the constant is obtained as follows:
k = 44/80
k = 0.55.
More can be learned about proportional relationships at https://brainly.com/question/7723640
#SPJ1
Divide the rational expressions and express in simplest form. When typing your answer for the numerator and denominator be sure to type the term with the variable first.\frac{\left(22y^2+59y+10\right)}{\left(12y^2+28y-5\right)}\div \frac{\left(11y^2+46y+8\right)}{\left(24y^2-10y+1\right)}The numerator is AnswerThe denominator is Answer
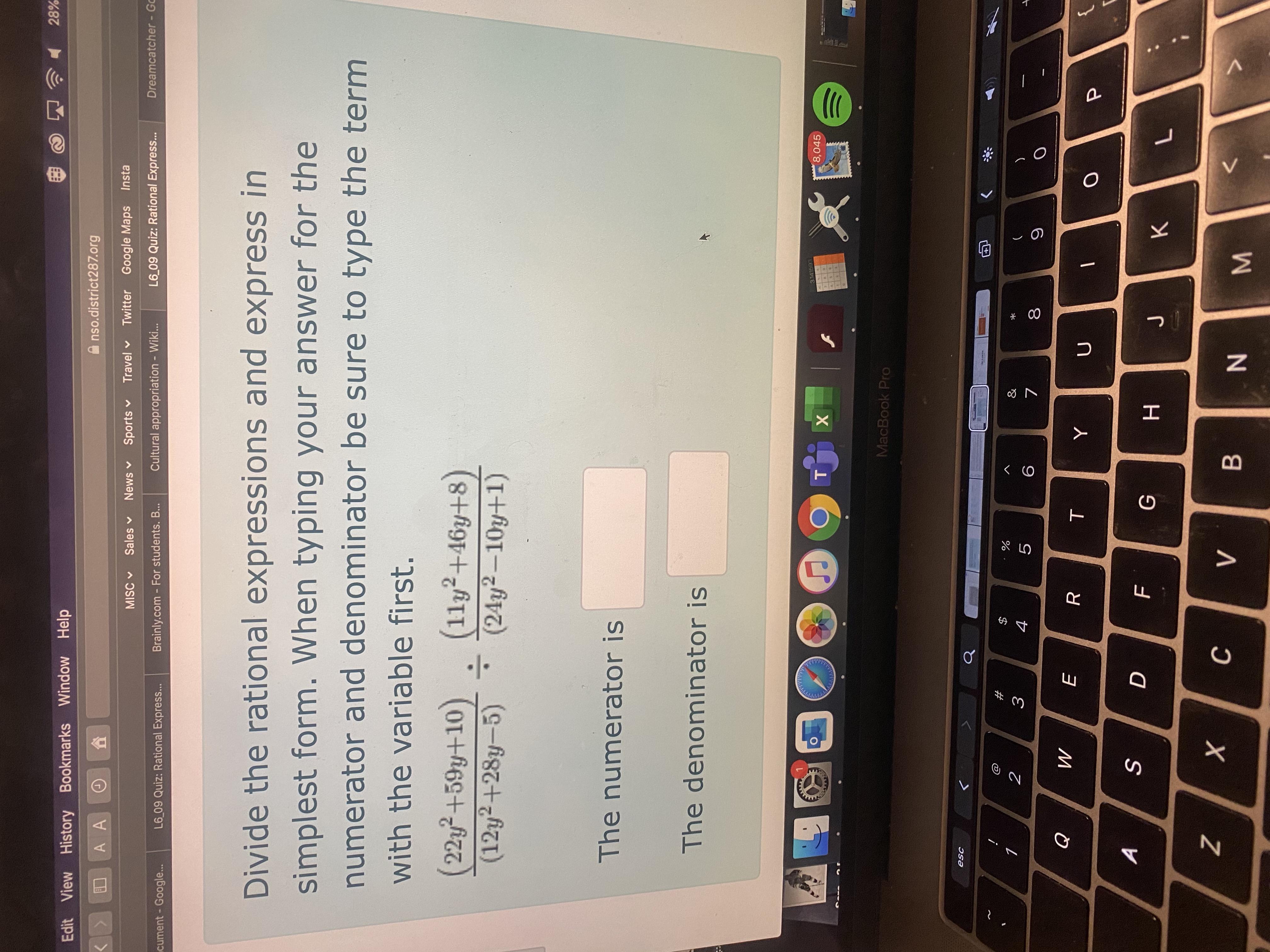
Answers
We need to divide the next rational expressions:
\(\frac{22y^2+59y+10}{12y^2+28y-5}\div\frac{11y^2+46y+8}{24y^2-10y+1}\)The first thing that we need to do is factorize the denominators and numerators, maybe we can cancel some terms.
The expression cant be factorized, now we are going to divide the terms:
Change the second fraction, now the denominator is the numerator:
Then change the division sign to the multiplication sing *
\(\frac{22y^2+59y+10}{12y^2+28y-5}\cdot\frac{24y^2-10y+1}{11y^2+46y+8}\)\(\frac{22y^2+59y+10}{12y^2+28y-5}=\frac{11y+2}{6y-1}\)\(\frac{11y+2}{6y-1}\cdot\frac{24y^2-10y+1}{11y^2+46y+8}\)Multiply the expression and reduce the fraction if it is possible:
Factorize the expression:
\(24y^2-10+1\text{ = (}6y-1)(4y-1)\)Now, we have the expression like this:
\(\frac{(11y+2)(6y-1)(4y-1)}{(6y-1)(11y^2+46y+8)}\)Cancel the similar terms 6y-1:
\(\frac{(11y+2)(4y-1)}{11y^2+46y+8}\)Factorize 11y^2 + 46y + 48
=(11y^2+2y) + (44y+8)
Factorize y from (11y^2+2y)
=y(11y+2)
Factorize 4 from 44y+8
= 4(11y+2)
So the solution is:
=(11y+2)(y+4)
\(\frac{(11y+2)(4y-1)}{(11y+2)(y+4)}\)Cancel common terms 11y+2
\(=\frac{4y-1}{y+4}\)Where 4y-1 is my numerator and y+4 my denominator.
Point F° is the image when point F is reflected over the line x = -2 and then over the line y = 3. The location of F° is (5, 7). Which of the following is the location of point F7
A(-5,-7)
B(-9,-1)
C(-1,-3)
D(-1,-13)
Answers
The location of the given point F7 is: B(-9, -1)
How to find the coordinates after transformation?There are different transformations such as:
Reflection
Translation
Rotation
Dilation
Since Point F' is the image when point F is reflected over the line x= -2 and then over the line y = 3. The location of F' is (5, 7).
So here we have to do graph the points, then connected the points i.e. 5 and 7. And, then reflect it over the line i.e. x = -2, and y = 3
So here the answer should be (-9,-1)
Read more about Transformation at: https://brainly.com/question/27224272
#SPJ1
two people start walking in different directions from the same point. one walks south at 4 mph and the other walks west at 3 mph. at what rate is the distance between the walkers increasing two hours later?
Answers
The distance between the walkers will increase at the rate of 5mph.
According to the question,
Two people start walking in different direction from same point.
Speed on the person walking west = 3mph
Speed of the person walking south = 4mph
The angle formed by the point connecting two persons will be = 90 degree
Applying Pythagoreans theorem,
\(p^{2} + b^{2} = h^{2}\)
\(4^{2} + 3^{2} = h^{2}\)
\(16 + 9 = h^{2}\)
\(h^{2} = 25\)
\(h = \sqrt{25}\)
h = 5mph.
Thus after two hours, the distance between same two persons will be 10m.
Learn more about time and distance at
https://brainly.com/question/11411949
What is the midpoint of H( 0, 0) and X(8, 6)
Answers
Answer:
The midpoint is (4, 3).
Step-by-step explanation:
to get the midpoint (x1+x2/2, y1+y2/2)
(0+8/2, 0+6/2)
(4, 3)
Marian Plunket owns her own business and is considering an investment. if she undertakes the investment, it will pay $28,000 at the end of each of the new 3 years. the opportunity requires an initial investment of $7,000 plus an additional investment at the end of the second year of $35,000. what is the NPV of this opportunity if the interest rate is 8% per year? Should Marian take it?
Answers
The NPV is positive, it is worth taking the Investment.
Net Present Value (NPV) is an assessment method that determines the attractiveness of an investment. It is a technique that determines whether an investment has a positive or negative present value.
This method involves determining the future cash inflows and outflows and adjusting them to their present value. This helps determine the profitability of the investment, taking into account the time value of money and inflation.The formula for calculating NPV is:
NPV = Σ [CFt / (1 + r)t] – CIWhere CFt = the expected cash flow in period t, r = the discount rate, and CI = the initial investment.
The given problem can be solved by using the following steps:
Calculate the present value (PV) of the expected cash inflows:
Year 1: $28,000 / (1 + 0.08)¹ = $25,925.93Year 2: $28,000 / (1 + 0.08)² = $24,009.11Year 3: $28,000 / (1 + 0.08)³ = $22,173.78Total PV = $72,108.82
Calculate the PV of the initial investment: CI = $7,000 / (1 + 0.08)¹ + $35,000 / (1 + 0.08)²CI = $37,287.43Calculate the NPV by subtracting the initial investment from the total PV: NPV = $72,108.82 – $37,287.43 = $34,821.39
Since the NPV is positive, it is worth taking the investment.
For more questions on Investment.
https://brainly.com/question/29227456
#SPJ8
Given find M for MON

Answers
Answer:
∠ MON = 15°
Step-by-step explanation:
∠ LOM + ∠ MON = ∠ LON, substitute values
9x + 44 + 6x + 3 = 77, that is
15x + 47 = 77 ( subtract 47 from both sides )
15x = 30 ( divide both sides by 15 )
x = 2
Thus
∠ MON = 6x + 3 = 6(2) + 3 = 12 + 3 = 15°
Solve by using the quadratic formula:
x2 - 6x + 7 = 0
Answers
Final Answer: \(x = 3 + \sqrt{2}, 3 - \sqrt{2}\)
Steps/Reasons/Explanation:
Question: Solve by using the quadratic formula: \(x^{2} - 6x + 7 = 0\).
Step 1: Use the Quadratic Formula.
\(x = \frac{6 + \sqrt[2]{2} }{2}, \frac{6 - \sqrt[2]{2} }{2}\)
Step 2: Simplify solutions.
\(x = 3 + \sqrt{2}, 3 - \sqrt{2}\)
~I hope I helped you :)~ The quadratic formulaic is attached in an image.

answer the question below please

Answers
Answer:
x=7
Step-by-step explanation:
AC=3x+3 AB=-1+2x and BC=11
AC = AB + BC
ALL THE STEPS:
3 X + 3 = - 1 + 2 X + 11
3 X + 3 = 2 X + 10
3 X + ( - 2 X ) + 3 = 2 X + ( - 2 X ) + 10
X + 3 = 10
X + 3 + ( - 3 ) = 10 + ( - 3 )
X = 7
Use the Laplace transform to solve the given initial value problem. y" - 4y - 60y = 0; y(0) = 12, y'(0) = 24 y(t)
Answers
Using the Laplace transform, the solution to the given initial value problem y" - 4y - 60y = 0; y(0) = 12, y'(0) = 24 y(t) is "y(t) = 6e^(8t) + 6e^(-8t)."
To use the Laplace transform to solve the given initial value problem, we need to follow these steps:
1. Apply the Laplace transform to both sides of the equation. Recall that the Laplace transform of the derivative of a function is given by sF(s) - f(0), where F(s) is the Laplace transform of f(t). Similarly, the Laplace transform of the second derivative is s^2F(s) - sf(0) - f'(0).
Taking the Laplace transform of the given equation, we have:
s^2Y(s) - sy(0) - y'(0) - 4Y(s) - 60Y(s) = 0
Substituting the initial values y(0) = 12 and y'(0) = 24, we get:
s^2Y(s) - 12s - 24 - 4Y(s) - 60Y(s) = 0
2. Combine like terms and rearrange the equation to solve for Y(s):
(s^2 - 4 - 60)Y(s) = 12s + 24
Simplifying further, we have:
(s^2 - 64)Y(s) = 12s + 24
3. Solve for Y(s) by dividing both sides of the equation by (s^2 - 64):
Y(s) = (12s + 24) / (s^2 - 64)
4. Decompose the right side of the equation into partial fractions. Factor the denominator (s^2 - 64) as (s - 8)(s + 8):
Y(s) = (12s + 24) / ((s - 8)(s + 8))
Using partial fractions decomposition, we can write Y(s) as:
Y(s) = A / (s - 8) + B / (s + 8)
where A and B are constants to be determined.
5. Solve for A and B by equating numerators:
12s + 24 = A(s + 8) + B(s - 8)
Expanding and rearranging the equation, we get:
12s + 24 = (A + B)s + (8A - 8B)
Comparing the coefficients of s on both sides, we have:
12 = A + B (equation 1)
0 = 8A - 8B (equation 2)
From equation 2, we can simplify it to:
A = B
Substituting this result into equation 1, we get:
12 = 2A
Therefore, A = 6 and B = 6.
6. Substitute the values of A and B back into the partial fractions decomposition:
Y(s) = 6 / (s - 8) + 6 / (s + 8)
7. Take the inverse Laplace transform of Y(s) to find the solution y(t):
y(t) = 6e^(8t) + 6e^(-8t)
Therefore, the solution to the given initial value problem y" - 4y - 60y = 0; y(0) = 12, y'(0) = 24 y(t) is:
y(t) = 6e^(8t) + 6e^(-8t)
To know more about "Laplace Transform":
https://brainly.com/question/29583725
#SPJ11
For the polynomial shown below, find f(1).
f(x) = 3x4 – x² + 4x – 2

Answers
Answer:
f(1)=3×1^4- 1^2+4×1-2
f(1)=3-1+4-2
f(1)=7-3
f(1)=4
Ans:4
Answer:
8
Step-by-step explanation:
Is 2x + 3 +7x equivalent to the expression 2(x+3) + 7x?
Answers
Answer:
No
Step-by-step explanation:
because if you use distribution on 2(x+3)+7x it gives you 2x+6=7x which does not equal 2x+3+7x
help me please༼ つ ◕_◕ ༽つ
The value of x is ___, and the value of y is ___.

Answers
Answer:
I think x is 60 and y is 50.
Step-by-step explanation:
70 + 50 = 120
180 - 120 = 60
x = 60
50 + 50 = 100
70 + 60 = 130
130 + 100 = 230
230 - 180 = 50
y = 50
I hope this helps u! :D
Answer:
x=60 y=50
Step-by-step explanation:
180 is equal to the whole triangle so 50+70=120 and 180-120= 60
the other triangle has a missing value by doing the same thing before we can figure out that the missing value is 70. 70+x which is 60 equals 130. A straight line is equal to 180 so 180-130= 50.
Hope I could help!