Consider the statement sqrt 300c9 = 10cx sqrt 3c. For what value of x is the statement true? x =
Answers
Answer:
Given the statement: Square root 300c^9 = 10c^x square root 3 c
⇒\sqrt{300c^9} =10c^x\sqrt{3c}
300c
9
=10c
x
3c
Squaring both sides we get;
(\sqrt{300c^9})^2= (10c^x\sqrt{3c})^2(
300c
9
)
2
=(10c
x
3c
)
2
Simplify:
300c^9 = 100c^{2x}(3c)300c
9
=100c
2x
(3c)
We know: a^m \cdot a^n = a^{m+n}a
m
⋅a
n
=a
m+n
then;
300c^9 = 300c^{2x+1}300c
9
=300c
2x+1
Divide both sides by 300 we get;
c^9 = c^{2x+1}c
9
=c
2x+1
On comparing both sides we have;
9 = 2x+19=2x+1
Subtract 1 from both sides we get;
8 = 2x
Divide both sides by 2 we have;
x = 4
Therefore, for the value of x =4 the given statement is true.
Answer:
x=4
Step-by-step explanation:
Related Questions
(-1,1,5)
9
8
7-
6
5
4
3₂
-3-2-1₁
(1,5)
(0,3)
Which exponential function is represented by the graph?
Of(x)=2(3¹)
Of(x)=3(3)
Of(x)=3(2)
O f(x) = 2(2¹)
Answers
The value of the equation that defines the function is f(x) = 3(5/3)ˣ
Finding an equation defining the functionFrom the question, we have the following parameters that can be used in our computation:
(0, 3) and (1, 5)
An exponential function is represented s
y = abˣ
Where,
a = y when x = 0
So, we have
y = 3bˣ
Using the other point, we have
3b = 5
This gives
b = 5/3
So, we have
f(x) = 3(5/3)ˣ
Hence, the equation defining f is f(x) = 3(5/3)ˣ
Read more about exponential function at
brainly.com/question/2456547
#SPJ1
HELP FIND THE VOLUME
ROUND TO THE NEAREST HUNDRETH
SHOW WORK PLEASE
WILL GIVE BRAINLIEST

Answers
5. Volume of sphere = 4/3 x pi xr ^3
Volume = 4/3 x 3.14 x 2^3 = 33.49 cubic feet.
6 . Volume of cylinder = pi x r^2 x height
Volume = 3.14 x 2^2 x 3 = 37.68 cubic meters
Which conic section is represented by the following equation?
5x2 – x + 5y2 – 3y + 4 = 0
Circle
Ellipse
Parabola
Hyperbola
Answers
Answer:
A. circle
Step-by-step explanation:

Answer:
A: Circle!
Step-by-step explanation:
Edge 2022
3.Write two polynomial functions whose quotient will be the same degree
as the divisor.
4.Write two polynomial functions whose quotient will have a degree of
zero.
Answers
Answer:0
Step-by-step explanation:
its right
If an average milk cow can give 4 2/3 gallons of milk per day. How much milk should a herd of 40 cows produce?
Answers
Answer:
\(\frac{560}{3}\) or 187
Step-by-step explanation:
First convert \(4\frac{2}{3}\) to a improper fraction
It would be \(\frac{14}{3}\)
Now multiply
\(\frac{14}{3}*\frac{40}{1} = \frac{560}{3}\)
Which is an intercept of the function y = log base of 3 x?
Answers
The x-intercept of the function y = log base 3 x is (1, 0)
What is logarithm ?
A logarithm is a mathematical function that is used to solve equations involving exponential expressions. It is the inverse operation of exponentiation.
The logarithm of a number y to a given base b is the power or exponent to which the base must be raised to yield the number y. In other words, if we have the equation \(b^x = y\), then the logarithm of y to the base b is x, which we can write as log base b y = x.
For example, if we take the base 2 and the number 8, the logarithm of 8 to base 2 is 3, because \(2^3 = 8\). This is written as log base 2 8 = 3.
According to the question:
The intercept of the function y = log base 3 x is the point where the graph of the function intersects either the x-axis or the y-axis. To find the intercepts, we set one of the variables to zero and solve for the other variable.
To find the y-intercept, we set x = 0 and evaluate the function:
y = log base 3 0
However, it is not possible to take the logarithm of 0 in any base, since 0 is not a positive number. Therefore, the function does not have a y-intercept.
To find the x-intercept, we set y = 0 and solve for x:
0 = log base 3 x
This equation can be rewritten in exponential form as:
\(3^0 = x\)
Since any number raised to the 0th power is 1, we have:
1 = x
Therefore, the x-intercept of the function y = log base 3 x is (1, 0).
To know more about logarithm visit:
https://brainly.com/question/30226560
#SPJ1
8 * 2 + 10 / 2 - 3 + 456643 *4 - 36 squared / 18 + 0 = ???????
Answers
Answer:
1.826.522
Step-by-step explanation:
16 +5 -3 + 1826572 + 4 -72 = 1.826.522
Suppose that LM = 36. Use the Triangle Proportionality Theorem to find PM. Round to the nearest tenth
Answers
Answer: 14.4units I think
Camila has 6 bags of candy. She can pour 1/3 of a bag of candy into a bowl. How many bowls of candy can Camila make in all?
Answers
Answer:
18 Bowls of Candy
Step-by-step explanation:
Camila has 6 bags of candy, and she can pour 1/3 of a bag into a bowl. To determine how many bowls of candy she can make in total, we need to divide the total amount of candy by the amount of candy per bowl.
Since Camila can pour 1/3 of a bag into a bowl, it means she can make 3 bowls of candy with a full bag.
Now, we can calculate the total number of bowls of candy:
Total bowls of candy = (Number of bags) x (Bowls per bag)
Total bowls of candy = 6 bags x 3 bowls per bag
Total bowls of candy = 18 bowls
Therefore, Camila can make a total of 18 bowls of candy with her 6 bags of candy.
Mystery Number:
I round to 375,400 when
rounded to the nearest hundred
have an odd hundreds digit,
tens digit, and ones digit
My tens and ones digits are
the same and both less than 7
What number am I?

Answers
Answer:
Step-by-step explanation:
375355
Which of the following shows a 90° counterclockwise rotation of the blue figure
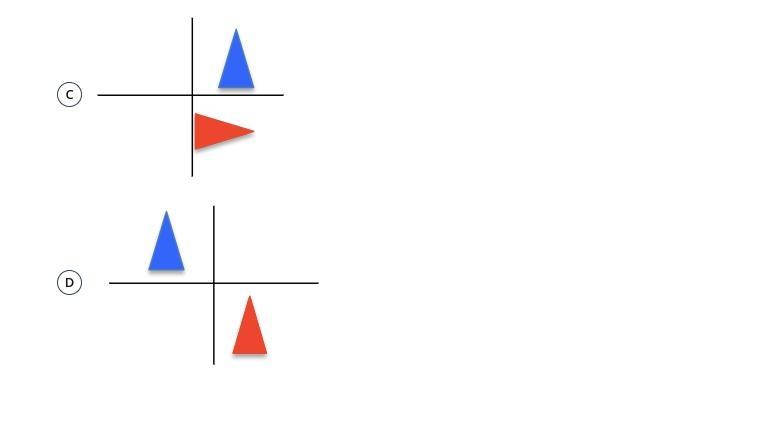

Answers
Hugo averages 60 words per minute on a typing test with a standard deviation of 6 words per minute. Suppose Hugo's words per minute on a typing test are normally distributed. Let X = the number of words per minute on a typing test: Then, X ~ N(60, 10)Suppose Hugo types 80 words per minute in a typing test on Wednesday. The z-score when x = 80 is tells you that r= 80 is____. This z-score tells you that x = 80 is____standard deviations to the____(right/left) of the mean,____Correctly fill in the blanks in the statement above.
Answers
The z-score for the given normally distributed data of typing test is 3.33 and its left and right p -value is equal to 0.9996 and 0.00043 respectively.
As given in the question,
Mean of the typing test 'μ' = 60 words per minutes
Standard deviation of the typing test 'σ' = 6 word per minutes
Number of words per minutes 'X' = 80
z- score = ( X - μ ) / σ
= ( 80 - 60 ) / 6
= 20 /6
= 3.33
z-score graph for the given data indicates the left tailed p -value .
Using table:
left tailed p -value = 0.9996
Right tailed p - value = 0.00043
two tailed p- value = 0.00086
Two tailed confidence level is given by 0.9991
Therefore , the z-score of the given mean and standard deviation is equal to 3.33 and left and right p -value is 0.9996 and 0.00043 respectively.
learn more about z- score here
brainly.com/question/15016913
#SPJ4
Are the events independent??
Best answer gets brainliest!!!

Answers
Answer:
C
Step-by-step explanation:
two events are independent if you can mulitply them to find their intersection
.5*.36= .18 which is obviously not .2
therefore they're not independent because they're not eqaul
Based on a $600 loan amount, rank the following companies from the lowest to highest annual percentage rate (APR)

Answers
The ranking from the lowest to highest APR for the given companies is A, B, D, C.
The correct option is b.
To rank the companies from the lowest to highest Annual Percentage Rate (APR) based on a $600 loan amount, we need to calculate the APR for each company. The formula to calculate APR is APR = (Fees / Loan Amount) * (365 / Terms of Loan).
Let's calculate the APR for each company:
For Company A:
APR_A = ($60 / $600) x (365 / 18) = 0.1 x 20.28 = 2.028%
For Company B:
APR_B = ($80 / $600) x (365 / 12) = 0.1333 x 30.42 = 4.054%
For Company C:
APR_C = ($90 / $600) x (365 / 10) = 0.15 x 36.5 = 5.475%
For Company D:
APR_D = ($110 / $600) x (365 / 14) = 0.1833 x 26.07 = 4.79%
Now, we can rank the companies from the lowest to highest APR:
Company A - APR: 2.028%
Company B - APR: 4.054%
Company D - APR: 4.79%
Company C - APR: 5.475%
To learn more about the percentage;
https://brainly.com/question/24159063
#SPJ1
If 142 adults are randomly selected, what is the probability that the sample mean would differ from the population mean by more than 1.5 kilograms
Answers
Complete question;
The mean weight of an adult is 76 kilograms with a variance of 100.
If 142 adults are randomly selected, what is the probability that the sample mean would differ from the population mean by more than 1.5 kilograms
Answer:
7.34% 0r 0.0734
Step-by-step explanation:
We have mean u = 76
Standard deviation = square root of variance
Sd = √100 = 10
N = 142
S = 10/√142
= 10/11.92
= 0.84
X is going to differ by more than 1.5 or less than 1.5
76-1.5 = 74.5
76+1.5 = 77.5
At x = 74.5
Z = (74.5-76)/0.84 = -1.79
At x = 77.5
Z = (77.5-76)/0.8 = 1.79
P value of z at -1.79 = 0.036
P value of z at 1.79 = 0.9633
0.9633-0.0367 = 0.9266
Which is 92.66% probability of differing by 1.5
Probability it differs by more:
P+92.66 = 100
P = 100-92.66
= 7.34% or 0.0734
Thank you!
To pay for a home improvement project that totals $20,000, a homeowner is choosing between two different credit card loans with an interest rate of 9%. The first credit card compounds interest quarterly, while the second credit card compounds monthly. The homeowner plans to pay off the loan in 10 years.
Part A: Determine the total value of the loan with the quarterly compounded interest. Show all work and round your answer to the nearest hundredth. (4 points)
Part B: Determine the total value of the loan with the monthly compounded interest. Show all work and round your answer to the nearest hundredth. (4 points)
Part C: What is the difference between the total interest accrued on each loan? Explain your answer in complete sentences. (2 points)
Please only responded if you know how to do it, will give the brainiest to however answers it correctly
Answers
The total value of the loan with quarterly compounded interest is approximately $45,288.38, while the total value of the loan with monthly compounded interest is approximately $45,634.84. The difference in total interest accrued is approximately $346.46.
Part A: To determine the total value of the loan with quarterly compounded interest, we can use the formula for compound interest:
A = P(1 + r/n)^(nt),
where:
A is the total value of the loan,
P is the principal amount (initial loan amount),
r is the interest rate (in decimal form),
n is the number of times interest is compounded per year,
and t is the number of years.
Given:
P = $20,000,
r = 9% or 0.09,
n = 4 (quarterly compounding),
t = 10 years.
Substituting the values into the formula, we have:
A = 20000(1 + 0.09/4)^(4*10).
Calculating this value, we find:
A ≈ $45,288.38.
Therefore, the total value of the loan with quarterly compounded interest is approximately $45,288.38.
Part B: To determine the total value of the loan with monthly compounded interest, we follow the same formula but with a different value for n:
n = 12 (monthly compounding).
Substituting the values into the formula, we have:
A = 20000(1 + 0.09/12)^(12*10).
Calculating this value, we find:
A ≈ $45,634.84.
Therefore, the total value of the loan with monthly compounded interest is approximately $45,634.84.
Part C: The difference between the total interest accrued on each loan can be calculated by subtracting the principal amount from the total value of each loan.
For the loan with quarterly compounding:
Total interest = Total value - Principal
Total interest = $45,288.38 - $20,000
Total interest ≈ $25,288.38.
For the loan with monthly compounding:
Total interest = Total value - Principal
Total interest = $45,634.84 - $20,000
Total interest ≈ $25,634.84.
The difference between the total interest accrued on each loan is approximately $346.46.
for such more question on compounded interest
https://brainly.com/question/20406888
#SPJ8
Can someone help me please?

Answers
Answer:
the only answer that makes sense would be the length
Point C has a coordinate of (-4, -6) and point D has a coordinate of (1, -6), how far are they apart?
Answers
The distance between points C and D is given as follows:
5 units.
How to calculate the distance between two points?Suppose that we have two points of the coordinate plane, and the ordered pairs have coordinates \((x_1,y_1)\) and \((x_2,y_2)\).
The shortest distance between them is given by the equation presented as follows, derived from the Pythagorean Theorem:
\(D = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\)
The coordinates for this problem are given as follows:
(-4, -6) and (1, -6).
Hence the distance is given as follows:
\(D = \sqrt{(-4 - 1)^2 + (-6 - (-6))^2}\)
D = 5 units.
More can be learned about the distance between two points at https://brainly.com/question/7243416
#SPJ1
#7 find the answer with the offering 20% discount

Answers
Given a discount of 20% and a manufacturer's coupon of $200, the price after the discount and coupon, (C ∘ D)(x), is 0.8x - 200.
What is a discount?A discount is an amount that reduces the price of a retail item.
Discounts are offered as rates and the discounted price is computed by multiplying the discount factor and the price.
Discount rate on offer = 20%
Discounting factor = 80% or 0.8 (100 - 20%)
Manufacturer's coupon off the price = $200
Let the price of the bureau = x
The price after the discount (discounted price) is given by D(x)
D(x) = 0.8x
The price after the coupon = C(x) = x - 200
The price after applying the discount and the coupon, (C ∘ D)(x) = 0.8x - 200
Learn more about discounts at https://brainly.com/question/28176129.
#SPJ1
Complete Question:Wilson's Warehouse sells a certain brand's bureau. They are offering a 20% discount in addition to accepting a manufacturer's coupon for $200 off. Let the price of the bureau be x. If the price after the discount is given by D(x) and the price after the coupon is C(x), find (C ∘ D)(x).
Work out the surface area of this cylinder,
12 cm
25 cm
Answers
Answer:
surface area = 74π
Step-by-step explanation:
The surface are of a cylinder is the sum of the area of the 2 circular base and the curved surface area.
A cylinder has 2 circular base and the curved surface region. Mathematically,
surface area = area of 2 circles + curved surface area
area of 2 circles = πr² + πr² = 2πr²
curved surface area = 2πrh
surface area = 2πr² + 2πrh
surface area = 2πr(r + h)
where
r = radius
h = height
assuming the r = 12 cm and h = 25 cm
Therefore, replacing the value in the formula
surface area = 2πr(r + h)
surface area = 2π(12 + 25)
surface area = 2π(37)
surface area = 74π
Please help me please 5th grade math

Answers
The length of the given rectangular cuboid is: 9 cm
How to find the volume of the rectangular prism?In geometry, a rectangular prism is defined as a polyhedron with two congruent as well as parallel bases. It is also referred to as a cuboid. A rectangular prism is one that possesses six faces, and then all the faces are located in a rectangle shape and possess twelve edges. Whenever its cross-section along the length, it is referred to as a prism.
The formula for the volume of a prism is given by the formula:
V = L * W * H
Where:
L is length
W is width
H is height
We have that Volume = 432 cm³
Thus:
6 * L * 8 = 432
48L = 432
L = 432/48
L = 9 cm
Read more about Volume of Prism at: https://brainly.com/question/23766958
#SPJ1
A cube is dilated by a scale factor of 3/4 to create a new cube.what is the surface area of the new cube
Answers
Therefore, the surface area of the new cube is (9/4) (6\(s^{2}\)) = 27/2\(s^{2}\).
What is surface area?Surface area refers to the total area that the surface of an object or a three-dimensional shape covers. It is measured in square units and includes all the faces, sides, and curved surfaces of the object. The surface area is a fundamental concept in geometry and is used to calculate various properties of objects, such as their volume, density, and material requirements. The formula for calculating the surface area of an object depends on the shape of the object. For example, the surface area of a cube is calculated by adding up the areas of its six faces, while the surface area of a sphere is calculated by multiplying the square of its radius by 4π.
Given by the question.
Let's assume that the original cube has a side length of s. Then, the surface area of the original cube is 6s^2, since a cube has 6 square faces with side length s.
When this cube is dilated by a scale factor of 3/4, the new side length becomes (3/4) s. The surface area of the new cube is then 6\((\frac{3}{4})^{2}\), which simplifies to 9/4 times the surface area of the original cube.
To more learn about cubic:
https://brainly.com/question/29249320
#SPJ1
Find the lowest common denominator.
1 1 2
----------- , ------------ , -------------
(x+2)2 (x-2)2 x2-4
Answers
The LCD of 1/(x+2)^2, 3/(x-2)^2, and 4/(x^2-4) is (x+2)^2(x-2)^2(x+2)(x-2) = (x+2)^3(x-2)^3.
To find the lowest common denominator (LCD) of three fractions, we need to identify the factors of each denominator and select those factors that are common to all denominators.The given fractions are: 1/ (x+2)^2, 3/ (x-2)^2, and 4/ (x^2-4).
The first denominator (x+2)^2 can be factored using the formula for the difference of two squares. The denominator of 3/(x-2)^2 can also be factored using the formula for the difference of two squares.
Finally, the denominator of 4/(x^2-4) can be factored using the formula for the difference of two squares and the formula for the sum of two squares.
So, 1/(x+2)^2, 3/(x-2)^2, and 4/(x^2-4) can be rewritten as follows:1/ (x+2)^2 = A/(x+2) + B/(x+2)^2. Multiplying both sides by (x+2)^2 gives:1 = A(x+2) + B ... (1)3/ (x-2)^2 = C/(x-2) + D/(x-2)^2.
Multiplying both sides by (x-2)^2 gives:3 = C(x-2) + D ... (2)4/ (x^2-4) = E/(x-2) + F/(x+2). Multiplying both sides by (x^2-4) gives:4 = E(x-2)(x+2) + F(x+2)(x-2) ... (3)
Now, we need to solve these equations for A, B, C, D, E, and F. First, we will solve equation (1) for A and B by substituting x = -2, which gives A = -1/4. Then we will substitute x = -2 again and solve for B, which gives B = 1/4. Next, we will solve equation (2) for C and D by substituting x = 2, which gives C = 3/4.
Then we will substitute x = 2 again and solve for D, which gives D = -3/4. Finally, we will solve equation (3) for E and F by substituting x = 2 and x = -2, which gives E = 1/2 and F = 1/2.
Now, we have A = -1/4, B = 1/4, C = 3/4, D = -3/4, E = 1/2, and F = 1/2. The LCD is the product of all the factors that appear in the denominators of the fractions, each raised to the highest power that appears.
To learn more about : LCD
https://brainly.com/question/1025735
#SPJ8
A variable is normally distributed with mean 6 and standard 2 deviation .
a. Find the percentage of all possible values of the variable that lie between 5 and 9.
b. Find the percentage of all possible values of the variable that exceed 1.
c. Find the percentage of all possible values of the variable that are less than 4.
Answers
The normal distribution is also known as the Gaussian distribution. The percentage of all possible values of the variable that are less than 4 is 15.87%.
What is a normal distribution?
The normal distribution, also known as the Gaussian distribution, is a symmetric probability distribution about the mean, indicating that data near the mean occur more frequently than data distant from the mean. The normal distribution will show as a bell curve on a graph.
A.) The percentage of all possible values of the variable that lie between 5 and 9.
P(5<X<9) = P(X<9) - P(5<X)
= P(z<1.5) - P(-0.5<z)
= 0.9332 - 0.3085
= 0.6247
= 62.47%
B.) The percentage of all possible values of the variable that exceed 1.
P(X>1) = 1 - P(X<-2.5)
= 1-0.0062
= 0.9938
= 99.38%
C.) The percentage of all possible values of the variable that are less than 4.
P(X<4) = P(X <4)
= P(z<-1)
= 0.1587
= 15.87%
Learn more about Normal Distribution:
https://brainly.com/question/15103234
#SPJ1
Student Enrollment
The enrollment at a local college has been decreasing linearly. In 2004, there where 975 students enrolled. By
2009, there were only 730 students enrolled. Determine the average rate of change of the school's enrollment
during this time period, and write a sentence explaining its meaning.
The average rate of change=
The enrollment at the college has been [Select an answer at a rate of
Select an answer v

Answers
The average rate of change of the school's enrollment during this time period is -49 students per year. This means that on average, the enrollment at the college has been decreasing by 49 students per year.
To determine the average rate of change of the school's enrollment during the given time period, we can use the formula:
Average rate of change = (Change in enrollment) / (Change in time)
The change in enrollment is calculated by subtracting the initial enrollment from the final enrollment, while the change in time is calculated by subtracting the initial year from the final year.
Given that in 2004 there were 975 students enrolled and in 2009 there were 730 students enrolled, we can calculate the change in enrollment:
Change in enrollment = 730 - 975 = -245 students
The change in time can be calculated as:
Change in time = 2009 - 2004 = 5 years
Now we can calculate the average rate of change:
Average rate of change = (-245 students) / (5 years) = -49 students per year
Therefore, the average rate of change of the school's enrollment during this time period is -49 students per year. This means that on average, the enrollment at the college has been decreasing by 49 students per year.
For more such questions on enrollment,click on
https://brainly.com/question/1101942
#SPJ8
What is 1/2 of 0.45x-1/4?
Answers
Answer:
0.45x−0.125
Step-by-step explanation:
0.45x-1/4
0.45x - 0.25 ÷ 2
0.45x−0.125
Show that x is not the factor of 2x*3-x*2-2x+1
Answers
Answer:
See explanation
Step-by-step explanation:
If we have a polynomial in x with x as a factor, we know that there will be no constant term. This arises because every term will be a multiple of x, and thus there will be know constant term.
Because there is a constant term in our polynomial, namely 1, x is not a factor of \(2x^3-x^2-2x+1\), as desired.
Answer: You divide using polynomial long division or synthetic division and if the remainder is 0 then it is a factor.
Step-by-step explanation:
A special drill is used at a construction site to dig holes. A hole is dug to a depth of 2.75 feet when the drill hits rock. The progress slows to 5/6 feet per hour of digging. The depth of the hole must be at least 10 1/2 feet by the end of the day to stay on schedule. What is the minimum amount of time the drill must continue at its present rate to complete the hole on schedule? Select from the drop-down menus to correctly complete the statement.
Answers
Answer:
9.3 hrs to finish
Step-by-step explanation:
(10.5 - 2.75)ft / (5/6 ft/hr) = 9.3 hrs to go
the value of a baseball players rookie card was $7.46 it then began to increase once the player retired in 1996. The value increased by $2.52 each year since then. Part A. how much was the baseball card worth in 1997? and then in 1998 and 1999?
Answers
Answer:
In 1997, the baseball card would be worth $7.46 + $2.52 = $9.98.
In 1998, the baseball card would be worth $9.98 + $2.52 = $12.50.
In 1999, the baseball card would be worth $12.50 + $2.52 = $15.02.
Step-by-step explanation:
In this problem, we are given the value of a baseball card in 1996, which is $7.46. We are also told that the value of the card increases by $2.52 each year since then. This means that in 1997, the value of the card increased by $2.52 compared to its value in 1996, so the value in 1997 would be $7.46 + $2.52 = $9.98. Similarly, in 1998, the value of the card increased by another $2.52 from its value in 1997, so the value in 1998 would be $9.98 + $2.52 = $12.50. In 1999, the value of the card increased by another $2.52 from its value in 1998, so the value in 1999 would be $12.50 + $2.52 = $15.02.
I’ll give brainly thingy please help me

Answers
Answer:
20%
Step-by-step explanation:
You would have to add 1200 and 300 to get the total amount of students which would be 1500.
Then put 1500 as the denominator and 300 as the numerator since we're talking about the number of students that did NOT wear their school colors. our fraction should then be 300/1500.
If you cross out 2 zeros on both numbers, you'll get 3/15. if you reduce that you get 1/5. 1/5= 20%