Answers
Answer:
Step-by-step explanation:
\(\sqrt[4]{(16a^4)^5}=(16a^4)^{\frac{5}{4}}\) [Since, \(\sqrt[n]{x}=x^{\frac{1}{n}}\)]
\(=(16)^{\frac{5}{4}}(a^4)^{\frac{5}{4}}\)
\(=(2^4)^{\frac{5}{4}}(a^4)^{\frac{5}{4} }\)
\(=(2^{4\times \frac{5}{4}})(a^{4\times \frac{5}{4}})\)
\(=2^5a^5\)
\(\sqrt[5]{(b^{\frac{1}{4}})^6}=\sqrt[5]{b^{\frac{6}{4}}}\)
\(=\sqrt[5]{b^{\frac{3}{2}}}\)
\(=(b^{\frac{3}{2}})^{\frac{1}{5} }\)
\(=b^{\frac{3}{10}}\)
\(\sqrt[3]{\frac{c^{15}}{c^9}}=\sqrt[3]{c^{15-9}}\)
\(=(c^6)^{\frac{1}{3}}\)
\(=c^{6\times \frac{1}{3} }\)
= c²
\(\sqrt[4]{16d^6\times 16d^{-5}}=\sqrt[4]{(2)^4(d^{6-5})(2)^4}\)
\(=\sqrt[4]{2^{(4+4)}d}\)
\(=\sqrt[4]{(2^8)d}\)
\(=2^{\frac{8}{4}}d^{\frac{1}{4}}\)
\(=2^2d^{\frac{1}{4}}\)
\(=4d^{\frac{1}{4}}\)
Related Questions
a random sample of 2 measurements is taken from the following population of values: 1, 2, 4, 5, 8. what is the probability that the range of the sample is 7?
Answers
The probability of the sample required where the range is 7 is 0.1 .
The range of a sample is the difference of the maximum and minimum values.
The range of the sample to be 7, the maximum and minimum values should be 8 and 1.
The outcomes required are (8,1).
The total probability of the sample for 2 measured values:
P=\(C_{5,2}\)
P=5!/(2!(5-2)!)
P=5!/(2!\(\times\)3!)
P=20/2
P=10
The probability of the outcome desired,
=(required outcomes)/(total outcomes)
=1/10
=0.1
The probability of the outcome required is 0.1 .
Learn more about probability here at:
https://brainly.com/question/14920385
#SPJ4
alex has 70% of her weekly paycheck automatically deposited into a savings account. this week, $35 is deposited. alex wants to know the total amount of her paycheck this week
Answers
Answer:
$50
Step-by-step explanation:
Total weekly paycheck = (total deposit/ percentage to be deposited)
Therefore, Weekly paycheck = ($35/70%)
Weekly paycheck = $50.
A sample of undergraduates at OSU were given an IQ test. The mean was110 and the standard deviation was 10. Draw a sketch of the data.
a. What percent scored below a 90 on the IQ test?
b. What percent scored higher than a 115? Lower than a 115?
c. If you wanted to find the top 15% of students, what would be the cutoffscore?
d. The middle 36% of students fall between what two scores?
e. What percentage of students fall between 95.6 & 105?
Answers
A normal distribution curve with mean 110 and standard deviation 10. Percentages of students scoring below 90, higher than 115, lower than 115, and between IQ score cut offs for the top 15% and the middle 36% of students were 105.7 and 114.3. The percentage of students falling between IQ scores of 95.6 and 105 is 23.5%..
To find the percentage of students who scored below a 90, we need to find the area under the normal distribution curve to the left of 90. Using a standard normal distribution table or calculator, we find that this area is about 0.16 or 16%.
To find the percentage of students who scored higher than a 115, using a standard normal distribution table or calculator, we find that this area is about 0.16 or 16%. To find the percentage of students who scored lower than a 115, we need to find the area under the normal distribution curve to the left of 115, which is about 84%.
To find the IQ score cutoff for the top 15% of students, using a standard normal distribution table or calculator, we find that the z-score is about 1.04. We can then use the formula z = (x - μ) / σ to solve for x, the IQ score cutoff:
1.04 = (x - 110) / 10
x = 121.04
So the IQ score cutoff for the top 15% of students is about 121.04.
To find the IQ scores, using a standard normal distribution table or calculator, we find that the z-scores are about -0.43 and 0.43. We can then use the formula z = (x - μ) / σ to solve for x, the IQ score cutoffs:
-0.43 = (x - 110) / 10
x = 105.7
0.43 = (x - 110) / 10
x = 114.3
So the IQ score cutoffs for the middle 36% of students are about 105.7 and 114.3.
To find the percentage of students who fall between IQ scores of 95.6 and 105, we find that the z-scores are about -1.04 and -0.46. Using a standard normal distribution table or calculator, we find that the area between these z-scores is about 0.235 or 23.5%.
To know more about normal distribution curve:
https://brainly.com/question/15395456
#SPJ4
10x^2-x-2=0 solve by factoring
Answers
X= -1 , 1/5
The probability density function shown models the amount of rainfall per year for a certain location. If the area of each square on the grid is 0.05, estimate the probability that the rainfall for the year is less than 8 inches.
Answers
Answer:
0.45
Step-by-step explanation:
Hope this helps
Correct me if this is wrong
find a vector function, r (t), that represents the curve of intersection of the two sur- faces. the cylinder x2 y2 = 16 and the surface z = x2 − y2
Answers
A vector function r(t) that represents the curve of intersection of the two surfaces is given by:r(t) = 〈2cos(t), 2sin(t), 4cos(t)sin(t)〉, 0 ≤ t < 2π.
A vector function r(t) that represents the curve of the intersection of the two surfaces is given by:
r(t) = 〈2cos(t), 2sin(t), 4cos(t)sin(t)〉, 0 ≤ t < 2π
The cylinder and the surface intersect at the curve of intersection on which x2 y2 = 16 and z = x2 − y2 .Therefore, to find the vector function r(t) that represents the curve of the intersection of the two surfaces, we need to solve both the equations and then represent the equations in terms of a single variable, t.
A vector function in terms of t is then obtained, whose components are the corresponding solutions of the equations. In this case, the solutions are:
x = 2cos(t), y = 2sin(t), and z = 4cos(t)sin(t)
For any value of t, these values will satisfy both equations,
x² + y² = 4 and z = x² - y². Therefore, the vector function r(t) that represents the curve of intersection of the two surfaces is:
r(t) = 〈2cos(t), 2sin(t), 4cos(t)sin(t)〉, 0 ≤ t < 2π
Therefore, a vector function r(t) that represents the curve of intersection of the two surfaces is given by:r(t) = 〈2cos(t), 2sin(t), 4cos(t)sin(t)〉, 0 ≤ t < 2π.
To know more about the vector function, visit:
brainly.com/question/33066980
#SPJ11
URGENT ‼️
WRITE AN Equation OF THE LIKE BELOW
Answers
\(\displaystyle\\Answer:\ y=\frac{x}{3}-3\)
Step-by-step explanation:
\((0,-3)\ \ \ \ \ (6,-1)\)
\(\displaystyle\\ Equation\ of\ the\ line\\\\\boxed {\frac{x-x_1}{x_2-x_1} =\frac{y-y_1}{y_2-y_1} }\)
\(\displaystyle\\x_1=0\ \ \ \ x_2=6\ \ \ \ \ y_1=-3\ \ \ \ \ y_2=-1\\\\\frac{x-0}{6-0}=\frac{y-(-3)}{-1-(-3)}\\\\\frac{x}{6}=\frac{y+3}{-1+3} \\\\\frac{x}{6} =\frac{y+3}{2} \\\\Multiply\ both\ parts\ of \ the\ equation \ by \ 2:\\\\\frac{x}{3}=y+3\\\\\frac{x}{3}-3=y+3-3\\\\ \frac{x}{3} -3=y \\\\Thus,\\\\y=\frac{x}{3}-3\)
discuss how discrete mathematics led to fewer cultural distinctions and where mathematics became more a unifying language of its own.
Answers
Discrete mathematics is a branch of mathematics that deals with objects that can assume only distinct, separated values and can be counted. It has played a significant role in reducing cultural distinctions by providing a unifying language for the field of mathematics and a common understanding for solving problems across cultures.
Through discrete mathematics, people from different backgrounds and cultures can communicate and collaborate more effectively, breaking down cultural barriers and promoting unity.
For example, discrete mathematics has been used to create algorithms that solve complex problems in computer science, cryptography, and optimization, making it possible for people from different cultures to work together to solve these problems.
Additionally, the standardization of mathematical language and symbols through discrete mathematics has made it easier for people to understand and share mathematical ideas across cultures, further promoting unity and reducing cultural distinctions.
To know more about Discrete mathematics click on the link below:
https://brainly.com/question/27247288#
#SPJ11
Find the volume of the prism
Answers
Answer:
A prism is a polyhedron with two parallel, congruent faces called bases that are polygons
Identify the sample space of the probability experiment: Answering a true or false question.
A) 1
B)2
C)4
D)5
Answers
Answer:
there are 5
Step-by-step explanation:
"im different"
The sample space of the statement is 2.
What is sample space?"A sample space is a collection or a set of possible outcomes of a random experiment. The sample space is represented using the symbol, “S”. The subset of possible outcomes of an experiment is called events. A sample space may contain a number of outcomes that depends on the experiment. If it contains a finite number of outcomes, then it is known as discrete or finite sample spaces."
"The samples spaces for a random experiment is written within curly braces “ { } “. There is a difference between the sample space and the events."
The given statement is "Answering a false question"
Sample space of the following is S = {True, False}
Hence B is the correct option.
To know more about sample space here
https://brainly.com/question/17144524
#SPJ2
Can someone help with problems fivethroughseven
Answers
Answer:
5) 15120
6) 11880
7) 336
Step-by-step explanation:
The formula for permutation where mPn is m!/(m-n)!
Applying this to question 5, we get 9!/4!, which is 15120.
For question 6, we get 12!/8!, which is 11880.
For question 7, we get 8!/5!, which is 336.
Write an expression that represents the height of a tree that begins at 6.7 feet and increases by 2.6 feet per year. Let t represent the number of years.
Answers
The expression for the height of a tree with a starting height of 6.7 feet and annual growth of 2.6 feet is h=6.7+2.7t.
What is a function?It is described as a particular kind of relationship, and each value in the domain is associated with exactly one value in the range according to the function. They have a predetermined domain and range.
It is given that, the term used to describe a tree's height starts at 6.7 feet and grows by 2.6 feet per year.
Expressions are made up of variables and constants together with mathematical operators.
Let's say that h is a tree's height and that t is the number of years.
For the specified condition, the resulting expression,
h=6.7+2.7t
Thus, the expression for the height of a tree with a starting height of 6.7 feet and annual growth of 2.6 feet is h=6.7+2.7t.
Learn more about the function here:
brainly.com/question/5245372
#SPJ1
The continuous random variable X has a probability density function (pdf) given by f(x) Şi- & for 0 < x < 2 lo otherwise Part(a) Find the median of X, correct to 2 decimal places. 0.59 Part(b) Find P(X >>). Give your answer as a decimal, correct to 2 decimal places. 0.56 Part(c) Two independent observations of X are taken. Find the probability correct to 2 decimal places that one is less than and the other is greater than 2. The order in which we take observations matters. 0.25 Part(d) Find Var(X), correct to 2 decimal places. 0.22 Part(e) Find E(X), correct to 2 decimal places. 0.75 Part(f) Find the value of q such that P(X
Answers
The median of X is 1; P(X > 2) = 0; P(one observation < 2 and the other > 2) = P(X < 2) * P(X > 2) = 0 * 0 = 0; Var(X) is approximately 0.33; E(X) is 1 and the value of q such that P(X < q) = 0.95 is 1.9.
(a) To find the median of X, we need to find the value of x for which the cumulative distribution function (CDF) equals 0.5.
Since the PDF is given as f(x) = 1/2 for 0 < x < 2 and 0 otherwise, the CDF is the integral of the PDF from 0 to x.
For 0 < x < 2, the CDF is:
F(x) = ∫(0 to x) f(t) dt = ∫(0 to x) 1/2 dt = (1/2) * (t) | (0 to x) = (1/2) * x
Setting (1/2) * x = 0.5 and solving for x:
(1/2) * x = 0.5; x = 1
Therefore, the median of X is 1.
(b) To find P(X > x), we need to calculate the integral of the PDF from x to infinity.
For x > 2, the PDF is 0, so P(X > x) = 0.
Therefore, P(X > 2) = 0.
(c) To find the probability that one observation is less than 2 and the other is greater than 2, we need to consider the possibilities of the first observation being less than 2 and the second observation being greater than 2, and vice versa.
P(one observation < 2 and the other > 2) = P(X < 2 and X > 2)
Since X follows a continuous uniform distribution from 0 to 2, the probability of X being exactly 2 is 0.
Therefore, P(one observation < 2 and the other > 2) = P(X < 2) * P(X > 2) = 0 * 0 = 0.
(d) The variance of X can be calculated using the formula:
Var(X) = E(X²) - [E(X)]²
To find E(X²), we need to calculate the integral of x² * f(x) from 0 to 2:
E(X²) = ∫(0 to 2) x² * (1/2) dx = (1/2) * (x³/3) | (0 to 2) = (1/2) * (8/3) = 4/3
To find E(X), we need to calculate the integral of x * f(x) from 0 to 2:
E(X) = ∫(0 to 2) x * (1/2) dx = (1/2) * (x²/2) | (0 to 2) = (1/2) * 2 = 1
Now we can calculate the variance:
Var(X) = E(X²) - [E(X)]² = 4/3 - (1)² = 4/3 - 1 = 1/3 ≈ 0.33
Therefore, Var(X) is approximately 0.33.
(e) The expected value of X, E(X), is given by:
E(X) = ∫(0 to 2) x * f(x) dx = ∫(0 to 2) x * (1/2) dx = (1/2) * (x²/2) | (0 to 2) = (1/2) * 2 = 1
Therefore, E(X) is 1.
(f) The value of q such that P(X < q) = 0.95 can be found by solving the following equation:
∫(0 to q) f(x) dx = 0.95
Since the PDF is constant at 1/2 for 0 < x < 2, we have:
(1/2) * (x) | (0 to q) = 0.95
(1/2) * q = 0.95
q = 0.95 * 2 = 1.9
Therefore, the value of q such that P(X < q) = 0.95 is 1.9.
Learn more about cumulative distribution function here:
https://brainly.com/question/30402457
#SPJ11
local bank is using Winters' method with α = 0.2,
β = 0.1, and γ = 0.5 to forecast the number of
customers served each day. The bank is open Monday through Friday.
At the end of the previous week,
Answers
The exact forecasted number of customers to be served on each of the next five business days, rounded to one decimal place, are as follows:
Tuesday: 389.1
Wednesday: 368.7
Thursday: 326.5
Friday: 510.9
To forecast the number of customers served on each of the next five business days using Winters' method, we need to follow these steps:
Calculate the seasonal factor for each day by multiplying the seasonal index by the level.
Monday: 1.10 × 20 = 22
Tuesday: 0.95 × 20 = 19
Wednesday: 0.90 × 20 = 18
Thursday: 0.80 × 20 = 16
Friday: 1.25 × 20 = 25
Update the level and trend using the following formulas:
New Level = α × (Actual Value / Seasonal Factor) + (1 - α) × (Previous Level + Previous Trend)
New Trend = β × (New Level - Previous Level) + (1 - β) * Previous Trend
For Tuesday:
New Level = 0.2 × (30 / 22) + 0.8 × (20 + 1) = 20.3636
New Trend = 0.1 × (20.3636 - 20) + 0.9 × 1 = 0.0364
Forecast the number of customers served on each subsequent day using the formula:
Forecast = (New Level + Forecasted Trend) × Seasonal Factor
Tuesday Forecast = (20.3636 + 0.0364) × 19 = 389.0909
Wednesday Forecast = (20.3636 + 0.0364) × 18 = 368.7273
Thursday Forecast = (20.3636 + 0.0364) × 16 = 326.5455
Friday Forecast = (20.3636 + 0.0364) × 25 = 510.9091
Therefore, the forecasted number of customers to be served on each of the next five business days, rounded to one decimal place, are as follows:
Tuesday: 389.1
Wednesday: 368.7
Thursday: 326.5
Friday: 510.9
The question should be: A local bank is using Winters' method with α = 0.2, β= 0.1, and γ = 0.5 to forecast the number of customers served each day. The bank is open Monday through Friday. At the end of the previous week, the following seasonal indexes have been estimated: Monday, 1.10; Tuesday, 0.95; Wednesday, 0.90; Thursday, 0.80; Friday, 1.25. Also, the current estimates of level and trend are 20 and 1. After observing that 30 customers are served by the bank on this Monday, forecast the number of customers who will be served on each of the next five business days. Round your answers to one decimal place, if necessary.
Read more on Seasonal index here: https://brainly.com/question/31959139
#SPJ11
there are 20 cars contesting a race. the first three cars completing the race will be awarded prizes. in how many ways can the prizes be awarded?
Answers
There are 6,840 ways to award the prizes to the first three cars completing the race.
Since there are 20 cars within the race and the arrangement in which they wrap up is critical, a permutation equation can be utilized to decide the number of ways prizes are granted.
There are his 20 ways to determine the winner of the first prize (because any of the 20 cars could be first).
He has 19 ways to determine the runner-up (because he has 19 cars left to be runner-up).
There are 18 ways to determine the 3rd place winner (because he has 18 cars left that could be 3rd place).
Using the multiplication principle, the total number of ways to award prizes is:
20 x 19 x 18 = 6,840
So there are 6,840 ways to award prizes to the top 3 cars that finish the race.
learn more about multiplication principle
brainly.com/question/17514196
#SPJ4
Which is a true statement about the transformation?
A.) Triangle ABC was translated 8 units left and 3 units up.
B.) The pre-image is in quadrant II.
C.) The orientation of the figure was changed.
D.) The orientation of the vertices was changed
HELP ASAP
Answers
Answer: the answer is B
Step-by-step explanation:
Answer:b
Step-by-step explanation:
Calculate pooled variance: n1 = 11n2 = 21df1 = 10df2 = 20s1 = 5.4SS1 = 291.6SS2 = 12482
Answers
The pooled variance is 126.48.
To calculate the pooled variance, we use the formula:
sp^2 = (SS1 + SS2) / (df1 + df2)
where SS1 and SS2 are the sum of squares for each sample, df1 and df2 are the degrees of freedom for each sample (which are equal to the sample size minus one), and sp^2 is the pooled variance.
Using the values given in the question:
SS1 = 291.6
SS2 = 12482
df1 = 10
df2 = 20
n1 = 11
n2 = 21
s1 = 5.4
We can calculate the pooled variance:
sp^2 = (SS1 + SS2) / (df1 + df2)
sp^2 = (291.6 + 12482) / (10 + 20)
sp^2 = 126.48
Therefore, the pooled variance is 126.48.
To learn more about pooled visit:
https://brainly.com/question/31352725
#SPJ11
Find the value of (1.52 x 〖10〗^5) + (5.4 x 〖10〗^4)
Answers
Answer:three significant figures: the 4, the 1, and the 8. This is ... 3) 7.09 x 10¯5 - three significant figures. ... Here is how it would be written: 9.160 x 104. ... Find the number with the LEAST number of digits in the decimal portion. ... The first value in the problem, with three significant places to the right of the decimal point, ...
Missing: (5.4 | Must include: (5.4
Step-by-step explanation:
☽------------❀-------------☾
Hi there!
~
\((1.52\ \times 10^5)+(5.4\times 10^4)\)
\(= (1.52)(10000)+5.4(10^4)\)
\(= 150000 + 5.4(10^4)\)
\(= 150000 + (5.4) (10000)\)
\(= 150000 + 54000\)
\(=20600\)
❀Hope this helped you!❀
☽------------❀-------------☾
The volume of a cube is 48x^6y^5 cubic units. If the length is 6x^3y and the width is 4x^2y^3, what is the height? (V=l*w*h)
Answers
The height of the cube calculated from volume 48x⁶y⁵ cubic units, length 6x³y and breadth 4x²y³ is 2xy units.
What is a cuboid?A cuboid is a six-sided solid known as a hexahedron. Quadrilaterals make up its faces. Cuboid is short for "like a cube." A cuboid is similar to a cube in that a cuboid may become a cube by varying the lengths of the edges or the angles between the faces.
Features of a Cuboid :
There are 6 faces, 12 edges, and 8 vertices on a cuboid.All of the cuboid's faces have rectangular shapes.The cuboid's opposing edges are parallel to one another.The three dimensions of a cube are length, width, and height.All of the angles created at the cuboid's vertices are 90 degree angles.A cube is a specific instance of a cuboid in which the length, width, and height are all equal. Accordingly, a cuboid is a cube.
The Volume of the cube is 48x⁶y⁵ cubic units
The length of the cube is 6x³y unit
Breadth of the cube is 4x²y³ unit
The height of the cube be H
We know,
volume(V) = length(L) * breadth(B) * height(H)
⇒ height = V/L*B = (48x⁶y⁵)/(6x³y)*(4x²y³)
⇒ height = (48x⁶y⁵)/(24x⁵y⁴) = 2xy
The height of the cube calculated from volume 48x⁶y⁵ cubic units, length 6x³y and breadth 4x²y³ is 2xy units.
To learn more about Cubes refer to :
https://brainly.com/question/21442836
#SPJ1
Find the domain of the function. g(x)=ln(x−3) The domain of g is (Type your answer in interval notation.)
Answers
The domain of the function g(x) = ln(x-3) is (3, +∞) in interval notation. To find the domain of the function g(x) = ln(x-3), we need to determine the values of x for which the function is defined.
1. The natural logarithm function ln(x) is defined only for positive values of x. Therefore, the expression inside the logarithm, x-3, must be greater than zero.
2. Set x-3 > 0 and solve for x:
x-3 > 0
x > 3
3. This inequality tells us that x must be greater than 3 for the function to be defined.
4. However, note that x cannot be equal to 3, as ln(0) is undefined.
5. Therefore, the domain of the function g(x) = ln(x-3) is all values of x greater than 3, excluding 3 itself.
6. In interval notation, we represent this as (3, +∞), where the open parenthesis indicates that 3 is not included in the domain, and the plus sign indicates that the domain extends indefinitely to the right.
In summary, the domain of the function g(x) = ln(x-3) is (3, +∞) in interval notation, indicating that x must be greater than 3 for the function to be defined.
To learn more about domain, click here: brainly.com/question/13109733
#SPJ11
PLEASE HELP MY GROUP
Answers
Answer:
A) 1006.7625
B) 2893.824
C) 2712.96
D) 111.784
Step-by-step explanation:
If A = {4, 7, 10, 13, 17) and B = {3, 5, 7, 9), then which of the following statements Is true?
BCA
AUB=(7)
BCB
Answers
B isn’t a proper subset of A because A doesn’t have elements 3, 5, and 9. A U B = {4, 7, 10, 13, 17, 3, 5, 9}, not {7}. Only B is a subset of B is true because every set is a subset of itself.
Or watch a video leroy is a citizen scientist for a monarch butterfly project. every week, he visits a local patch of milkweed and counts the number of monarch larvae on the plants. last week, leroy didn't count many larvae. this week, he counts 29 larvae on the milkweed. for both weeks, leroy's total count is 41 larvae.
Answers
Leroy's count for last week is 21 larvae.
Define subtractionThe process of determining the difference between two integers is called subtraction, which is a fundamental arithmetic operation and is represented by the symbol (-). To determine the difference between two numbers, perform the subtraction process. When you remove a few items from a group of things, the group gets smaller.
Given, total count for both week is 41 larvae
Count for this week is 29 larvae.
Now, find the count for last week,
count = 41 - 29
= 12
Therefore, Leroy's count for last week is 12 larvae.
To know more about subtraction, visit:
https://brainly.com/question/2346316
#SPJ4
The complete question is:
Leroy is a citizen scientist for a monarch butterfly project. Every week, he visits a local patch of milkweed and counts the number of monarch larvae on the plants. Last week, Leroy didn't count many larvae. This week, he counts 29 larvae on the milkweed. For both weeks, Leroy's total count is 41 larvae. Find Leroy's count for last week.
y + 2x = 4 How do I complete this?
Answers
Here’s how to solve:
y+2x=4
-2x -2x
y=4-2x
4-2x + 2x =4
4=4
So if you’re trying to see if it is true, then your answer is that it’s true.
If you’re trying to find the linear equation, then your answer is y=-2x+4.
help please someone!!!
Answers
the correct answer is y=5
Answer:
The correct answer Is y=5 i belive
Step-by-step explanation: Hope dis helped UWU :3 Meme for u
What is the length of the line? Answer choices:
8
12
Square root of 60
Square root of 136
Distance between two points
Answers
Answer:
I think the answer. is 10
Answer:
square root of 136
Step-by-step explanation:
Khan Academy Answer
HELP!
Find f(-1) for f(x) = -3x + 2x”.
Answers
Answer:
f(-1) = 1
Step-by-step explanation:
f(-1) just means you plug -1 into the equation:
-3x + 2x
-3(-1) + 2(-1)
3 - 2
1
Hopefully this helps!
Brainliest please?
How to convert us dollar to thai baht?
Answers
Convert USD to THB, multiply amount of USD by the current exchange rate between USD and THB, which can be found on financial news or currency exchange websites, to get the equivalent amount in THB.
To convert US dollars (USD) to Thai baht (THB), you need to use the current exchange rate between the two currencies. Here are the steps to convert USD to THB:
Find the current exchange rate between USD and THB. This information can be found on financial news websites, currency exchange websites, or by contacting a bank or currency exchange service.
Multiply the amount of US dollars you want to convert by the current exchange rate to get the equivalent amount in Thai baht. For example, if the current exchange rate is 1 USD = 31.50 THB and you want to convert 100 USD to THB, the calculation would be:
100 USD x 31.50 THB/USD = 3,150 THB
Therefore, 100 USD is equal to 3,150 THB.
Note: The exchange rate between USD and THB can fluctuate over time, so make sure to use the current exchange rate for the most accurate conversion.
Learn more about exchange rate here:
https://brainly.com/question/29562028
#SPJ4
The m<1=4x-30 and the m<5=2x+50. Find m<1 and m<7.
A. M<1=130 and M<7=130
B. M<1=130 and M<7=50
C. M<1=50 and M<7=50
D. M<1=50 and M<7=130
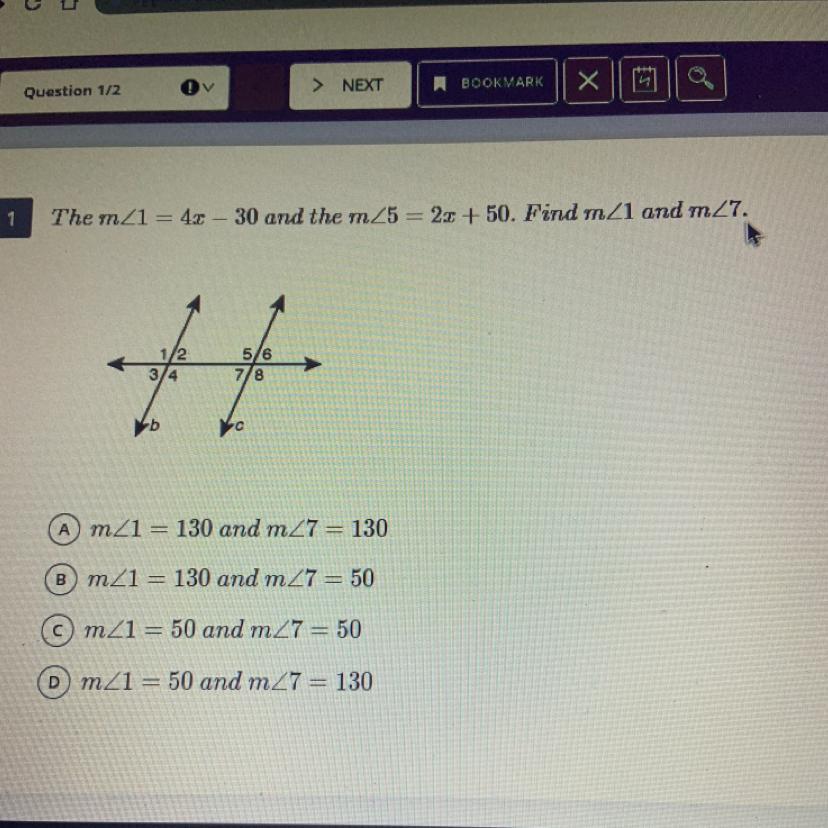
Answers
Answer:
D) m<1 = 50 m<7 = 130
Step-by-step explanation:
Lets set up the equation!
We know m<4 is 4x-30 and the m<5 is 2x + 50 due to alternate interior angles they are congruent so we can forge an equation, all we do is set them equal to each other!
4x-30 = 2x+50
Add 30 to both sides
4x = 2x +80
Subtract 2x from both sides.
2x = 80
Divide both sides by 2
x = 40
Now that we know x we can just plug it into the expression of m<4 to find m<1
4x-30
4(40)-30
80 - 30
50
m<4 = 50
Because m<1 and m<4 are vertical angles they are congruent!
m<1 = 50
We also know m<4 and m<5 are congruent so m<5 = 50 as well.
Because <7 is supplementary to <5 we know that the sum of both angles amount to 180.
x represents m<7
50 + x = 180
Now we solve by subtraction 50 from both sides
x = 130
m<7 = 130
Brainliest is appreciated!
Use the translation (x, y) (x – 8, y+4) to answer the question. What is the preimage of C' (-3, -10)?
Answers
The preimage of the point C'(x, y) = (- 3, - 10) is the point C(x, y) = (5, - 14).
What is the preimage of a point according to the translation formula?
In this question we find the coordinates of a point that is result of a translation. Translations are examples of rigid transformations, whose vector formula is shown below:
C'(x, y) = C(x, y) + T(x, y)
Where:
C(x, y) - Original pointC'(x, y) - Resulting point T(x, y) - Translation vectorPlease notice that the original point C(x, y) is the preimage of C'(x, y).
If we know that C'(x, y) = (- 3, - 10) and T(x, y) = (- 8, 4), then the preimage of the point C is:
(- 3, - 10) = C(x, y) + (- 8, 4)
C(x, y) = (- 3, - 10) - (- 8, 4)
C(x, y) = (- 3, - 10) + (8, - 4)
C(x, y) = (5, - 14)
The preimage is the point C(x, y) = (5, - 14).
To learn more on translations: https://brainly.com/question/12463306
#SPJ1