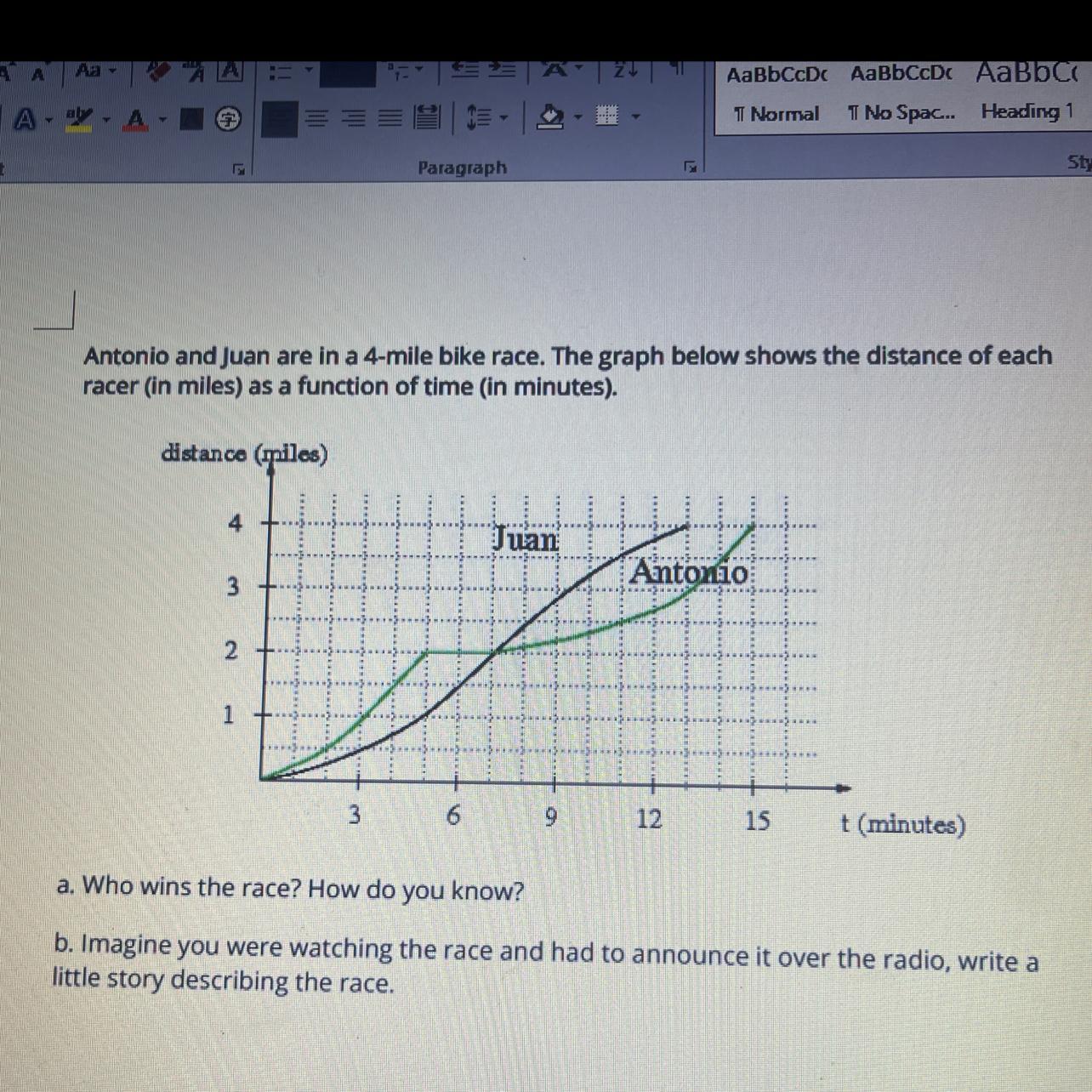
Antonio and Juan are in a 4-mile bike race. The graph below shows the distance of eachracer (in miles) as a function of time (in minutes).

Answer:

160 degrees

Step-by-step explanation:

Step 1: A straight line is 180 degrees. So 180 - 100, is 80 degrees. as the opposite angle measurement of the 100 degree.

Step 2: An isosceles triangle has two equal angle measurements, so two of its angles are 80 degrees.

Step 3: All angles in a triangle equal 180 degrees. So add them up (we will call the missing angle, Z)     180 = 80+80+Z.      which equals 180= 160+z

Step 4: Solve it. You subtract 160 from both side which comes out to 20 = Z.

Step 5: Now you have the opposite angle of X. Going back to step 1, A straight angle is 180 degrees. 180 - 20 = 160. X = 160 degrees

Answer:

140 days

Step-by-step explanation:

there are 7 days in 1 week so just multiply 20 by 7 which is 140, to make it easier multiply 2 by 7 which is 14 then add the 0 soo 140.

Hope this helps :)

The linear graph for the function having the features has been plotted and attached below.

What is a linear graph?

A graph is a diagram that depicts the relationship or connection between two or more quantities. Linear implies straight. The x and y coordinates of two points are connected by a straight line, or straight graph, to form a linear graph.

We are given that the x - intercept is 7 and the y - intercept is 2.

This means that the two points are (7, 0) and (0, 2).

Using these points, we will plot the linear graph. We know that linear graph is always a straight line. The same is shown in the graph below.

Hence, the graph of the function having particular features has been obtained.

Learn more about linear graph from the given link

https://brainly.com/question/30094272

#SPJ1

Answer:

\(\frac{8}{15}\) of a mile

Step-by-step explanation:

To find a segment of a fraction, you must first find the LCM of each value's denominator:

LCM - Lowest Common Multiple

The lowest common multiple is the number that shows up first in each number's multiple set.

Example: LCM of 4 and 6

Multiples of 4: 4, 8, 12, 16, 20

Multiples of 6: 6, 12, 18, 24, 30

Because 12 is the first number to show up in each multiple set, 12 is the LCM.

So, to be able to solve this problem easy, do the same with 5 and 3:

5, 10, 15, 20, 25

3, 6, 9, 12, 15

Since 15 is the first number in both sets, 15 is the LCM.

The next step is to multiply \(\frac{4}{5}\) by \(\frac{x}{x}\), x being the value that can be multiplied with the denominator to equal 15:

\(\frac{4}{5}\) × \(\frac{3}{3}\) = \(\frac{12}{15}\)

To find how much \(\frac{2}{3}\) of \(\frac{12}{15}\) is, multiply the fractions together:

\(\frac{12}{15}\) × \(\frac{2}{3}\) = \(\frac{24}{45}\)          

Simplify the fraction by dividing the numerator and denominator by 3.

\(\frac{24}{45}\) ÷ \(\frac{3}{3}\) = \(\frac{8}{15}\)

Because the fraction can't be simplified any further, Aimee has walked a total of \(\frac{8}{15}\) of a mile.

The mean absolute deviation of the set of numbers is 5/4

The set of numbers is given as:

1 1/2, 0, 4 and 2 1/2

Rewrite the set of numbers as:

1.5, 0, 4 and 2.5

Calculate the mean of the set using:

\(\bar x\) = Sum/Count

So, we have:

\(\bar x\) = (1.5 + 0 + 4 + 2.5)/4

Evaluate

\(\bar x\) = 2

The mean absolute deviation is then calculated as:

M.A.D = 1/n * ∑|x - \(\bar x\)|

So, we have:

M.A.D = 1/4 * [|1.5 - 2| + |0 - 2| + |4 - 2| + |2.5 - 2|]

Evaluate the absolute difference

M.A.D = 1/4 * [0.5 + 2 + 2 + 0.5]

Evaluate the sum

M.A.D = 1/4 * 5

Evaluate the product

M.A.D = 5/4

Hence, the mean absolute deviation of the set of numbers is 5/4

Read more about mean absolute deviation at

https://brainly.com/question/9495630

#SPJ1

Answer:

D) 1/5 e 1/3

Step-by-step explanation:

You have the following quadratic equation:

\(15x^2-kx+1=0\)           (1)

In order to find the values of x that are solution to the equation (1), you first find the solution for k in the following equation:

\(2(k-8)+3(-k+1)=-4k+11\\\\2k-16-3k+3=-4k+11\\\\2k-3k+4k=11+16-3\\\\3k=24\\\\k=8\)

Next, you replace the previous value of k in the equation (1) and you use the quadratic formula to find the roots:

\(15x^2-8x+1=0\\\\x_{1,2}=\frac{-(-8)\pm \sqrt{(-8)^2-4(15)(1)}}{2(15)}\\\\x_{1,2}=\frac{8\pm 2}{30}\\\\x_1=\frac{1}{5}\\\\x_2=\frac{1}{3}\)

Then, the roots of the equation (1) are

D) 1/5 e 1/3

The function is continuous in the domain x ≥ 3/4

Here we have a root function:

f(x) = ⁴√(4x - 3)

This is an even degree root function, so we have problems when the argument is negative.

Then the allowed values (where the function is defined, and thus, continuous) are:

4x - 3 ≥ 0

4x ≥ 3

x ≥ 3/4

There the function is continuous.

Learn more about continuous functions at:

https://brainly.com/question/18102431

#SPJ1

Answer:

\(\displaystyle \lim_{x \to 2} \frac{x}{f(x)+1} = +\infty\)

Step-by-step explanation:

From the graph, we can see that:

\(\displaystyle \lim_{x \to 2} f(x)= -1\)

From direct substitution, we have that:

\(\displaystyle \lim_{x \to 2} \frac{x}{f(x)+1}\Rightarrow \frac{(2)}{-1+1}\)

Evaluate:

\(\displaystyle = \frac{2}{0}=\text{Und.}\)

Saying undefined (or unbounded) would be correct.

However, note that as x approaches two, the value of y decreases in order to get to negative one. In other words, our function f will always be greater or equal to negative one (you can also see this from the graph). This means that as x approaches two, f(x) will approach -0.99, -0.999 and -0.9999 and so on until it reaches negative one and then go back up. Importantly, because of this, we can state that:

\(\displaystyle \lim_{x \to 2} \frac{x}{f(x)+1}=\frac{(2)}{-1+1} = +\infty\)

This is because for the denominator, the +1 will always be greater than the f(x). This makes this increase towards positive infinity. Note that limits want the values of the function as it approaches it, not at it.

Answer:

x = -3/2

Step-by-step explanation:

Lets first multiply the entire equation by 4 to get rid of the fractions.

1+2+4x = -3

3+4x = -3

4x = -6

x = -6/4

x = -3/2

Answer:

they are repetative situations

Step-by-step explanation:

Answer: B

Step-by-step explanation:

I just solved it

The correct answer is . The ordered pairs (a, b) of a function are (b, a) for the inverse function.

Answer:

A

Step-by-step explanation:

the equation of a circle in standard form is

(x - h)² + (y - k)² = r²

where (h, k ) are the coordinates of the centre and r is the radius

here (h, k ) = (4, 1 ) and r = 2 , then

(x - 4)² + (y - 1)² = 2² , that is

(x - 4)² + (y - 1)² = 4 ← equation of circle

The perimeter of the square will be 22

Answer:

The linear velocity of the cable ≅ 327 feet per minute.

Step-by-step explanation:

Given that the diameter of the drum = 8 feet

Radius of the drum = \(\frac{diameter}{2}\)

           = \(\frac{8}{2}\)

           = 4 feet

Radius of the drum = 4 feet

1 revolution = circumference of the drum

circumference of the drum = 2\(\pi\)r

where r is the radius.

So that;

circumference of the drum = 2 x \(\frac{22}{7}\) x 4

                                             = \(\frac{176}{7}\)

                                            = 25.143

circumference of the drum = 25.143 feet

The linear velocity of the cable = (13 x 25.143) feet per minute

                               = 326.859 feet per minute

The linear velocity of the cable ≅ 327 feet per minute.

The speed of an object is its distance traveled per unit time

The average speed required for the remainder of the trip 55.5

The reason the average speed value is correct is given as follows:

The known parameters;

The length of the first part of the trip, L = 218 mile

Duration of the time the sales person travels, t₁ = 2 hours and 15 minute

Average speed of travel, v₁ = 64 mph

The time at which the salesperson arrive at the destination, t₂ = 1 hour and 20 minutes

Required:

To find the average speed required for the remainder of the trip

Solution:

Distance traveled = Speed × Time

The distance traveled on the first part of the trip, d₁ = v₁ × t₁

(t₁ = 2 hours and 15 minute = 2.25 hours)

∴ d = 64 mph × 2.25 hours = 144 miles

The distance of the remainder part of the trip, d₂ = L - d₁

d₂ = 218 mile - 144 mile = 74 mile

The average speed required for the remainder of the trip, v₂, is given as follows;

\(v_2 = \dfrac{d_2}{t_2}\)

t₂ = 1 hour and 20 minutes = \(1\frac{1}{3} \ hour = \frac{4}{3} \, hour\)

Therefore;

\(v_2 = \dfrac{74 \ mile}{1\frac{1}{3} \ hour} = 55.5 \ mph\)

With the units left out, we have;

The average speed required for the remainder of the trip, v₂ = 55.5

Learn more about calculation of speed here:

https://brainly.com/question/13664094

https://brainly.com/question/17345820

https://brainly.com/question/13511093

Answer: its actually 900

Step-by-step explanation:

Answer:

Step-by-step explanation:

The upper and lower angles are vertical angles, so congruent:

  (5x -5)° = 55°

  x - 1 = 11 . . . . . . . divide by 5°

  x = 12

_____

The 55° angle and y° are a linear pair, so are supplementary.

  y° = 180° -55°

  y = 125 . . . . . . . simplify, divide by °

Answer:453rft

Step-by-step explanation:

Answer:

-1.6r + 1.8

Step-by-step explanation:

-1.6 (r+2) +5

^ the -1.6 can be distributed to the (r+2) because it's basically multiplying

that becomes --> -1.6r + -3.2 + 5

Now the -3.2 and 5 are like terms so they can be solved together

-> -3.2 + 5 = 1.8

Now, -1.6r and 1.8 are not like terms because 1.8 does not have an r attached to it so you cannot do nothing from there

your answer becomes = -1.6r + 1.8

If x is in the nullspace of A, then Ax = 0. Consider the augmented matrix

\(\left[\begin{array}{ccc|c}1&-1&2&0\\0&1&-3&0\end{array}\right]\)

Add row 2 to row 1 to get this into reduced-row echelon form:

\(\left[\begin{array}{ccc|c}1&0&-1&0\\0&1&-3&0\end{array}\right]\)

Then x = [x₁, x₂, x₃]ᵀ such that

x₁ - x₃ = 0

x₂ - 3 x₃ = 0

If you let x₃ = 1, you end up with x₁ = 1 and x₂ = 3, so x = [1, 3, 1]ᵀ.

More generally, if you let x₃ = y, then any vector of the form [y, 3y, y]ᵀ would belong to the nullspace.

Check that this is orthogonal to the rows of A :

[1, -1, 2] • [1, 3, 1]ᵀ = 1•1 + (-1)•3 + 2•1 = 1 - 3 + 2 = 0

[0, 1, -3] • [1, 3, 1]ᵀ = 0•1 + 1•3 + (-3)•1 = 0 + 3 - 3 = 0

\( \sf \longrightarrow \: 12 \times ( - 4) \times ( - 5)\)

\( \sf \longrightarrow \: 12 \times 20\)

\( \sf \longrightarrow \: 240\)

Answer:

The 36th derivative of f(x) = cos(2x) is \(2^{17}\)* cos(2x).

To find the 36th derivative of the function f(x) = cos(2x), we can apply the chain rule repeatedly. The chain rule states that if we have a composite function y = f(g(x)), then its derivative is given by dy/dx = f'(g(x)) * g'(x).

Let's start by finding the first few derivatives of f(x) = cos(2x):

f'(x) = -2sin(2x)

f''(x) = -4cos(2x)

f'''(x) = 8sin(2x)

f''''(x) = 16cos(2x)

We observe a pattern where the derivatives of cos(2x) alternate between sin(2x) and cos(2x), with the signs changing accordingly.

Based on this pattern, we can see that the 36th derivative will be:

f^(36)(x) =\((-1)^{17} * 2^{17} *\) cos(2x)

Simplifying this expression, we have:

f^(36)(x) = \(2^{17} * cos(2x)\)

Therefore, the 36th derivative of f(x) = cos(2x) is\(2^{17\) * cos(2x).

It's important to note that in this case, the number 36 is even, and since the derivatives of cos(2x) follow a repeating pattern every 4 derivatives, the sign (-1) raised to the power of 17 accounts for the change in sign in the 36th derivative.

For more such questions on derivative visit:

https://brainly.com/question/23819325

#SPJ8

The coordinates of each points are:

A = (-0.5, -5)

B = (0.8, -1.8)

C = (-2.6, -2.2)

D = (-1.5, -8.9)

E = (2.5, -6.5)

F = (-1.5, 3.1)

G = (-2.4, 4.1)

H = (1.5, 3)

I = (2.7, 1.5)

J = (-1.5, 0)

K = (-6.5, 0)

We have,

The coordinates of each point are in an ordered form.

i.e

(x, y)

x is the x-axis value.

y is the y-axis value.

Thus,

A = (-0.5, -5)

B = (0.8, -1.8)

C = (-2.6, -2.2)

D = (-1.5, -8.9)

E = (2.5, -6.5)

F = (-1.5, 3.1)

G = (-2.4, 4.1)

H = (1.5, 3)

I = (2.7, 1.5)

J = (-1.5, 0)

K = (-6.5, 0)

Learn more about coordinates here:

https://brainly.com/question/13118993

#SPJ1

Answer:

x = 2

Step-by-step explanation:

First, subtract 3 from both sides.

2x + 3 = 7

     - 3    -3

2x       = 4

Then, divide both sides by 2.

2x / 2 = 4 / 2

x = 2

Answer:

the solution for x is x = 2

Step-by-step explanation:

To solve for x, we need to get x by itself on one side of the equation. First, we can subtract 3 from both sides to get:

2x + 3 - 3 = 7 - 3

Simplifying the left side gives us:

2x = 4

Then, we can divide both sides by 2 to get:

2x / 2 = 4 / 2

Simplifying the left side gives us:

x = 2

Answer: 39

Step-by-step explanation:

30-8=22

22/2=11

11+2=13

13 times 3 =39

There is a Weak positive association between the amount of goals scored and the number of wins a hockey team has. Most of the data points fall between 4 goals scored and 5  number of wins. Causation cannot be established because their relationship was not in a controlled setting.

When if a relationship between two variables is said to be  negative, it is one that does not just necessarily mean that the association is weak. Although though both variables tend to increase in reaction to one another, a weak positive correlation depicts that the relationship is not very strong.

Therefore, even though  the data tells us that there is a weak positive relationship that exist between the two variables, it is vital to know that that correlation does not equal causation.

Learn more about data points from

https://brainly.com/question/30588709

#SPJ1

Answer:

c) 1

Step-by-step explanation:

Solving for the value of s,

→ 3s - 12 = -9

→ 3s = -9 + 12

→ s = 3/3

→ [ s = 1 ]

Thus, option (c) is correct.

1a) An equation that gives the width `y` of the book, if it has `x`-hundred pages printed on bond paper is; y = ¹/₂ + ¹/₄x

1b) Ledger paper has a thickness of 2/5 in. per `100` pages, the equation is; y = ¹/₂ + ²/₅x

2) The equation will be; y = ²/₃ +¹/₄x

1) We are told that the front cover and the back cover have a thickness of 1/4 inches and they also have a thickness of 1/4 inch. Thus;

The addition of both gives to the book thickness of;

1/4 + 1/4 = 1/2 inch, despite how many pages the book  has.

We are told that for every hundred pages, a thickness of 1/4 inch is added to the book, then the equation is:

y = ¹/₂ + ¹/₄x

where;

y is the width of the book in inches.

x is every hundred pages printed on bond paper.

1b) If ledger paper has a thickness of 2/5 in. per 100 pages, then the equation is now;

y = ¹/₂ + ²/₅x

2) If both front and back covers now, have a thickness of 1/3 inches instead of 1/4 inches each, then the equation will be;

y = 2(1/3) +¹/₄x

y = ²/₃ +¹/₄x

Read more about Algebraic Word Problems at; https://brainly.com/question/21405634

#SPJ1