Answer the question and explain your answer. I will be marking brainiest! If you have the correct answer and explain why it’s correct, I will probably pick YOU as brainiest! :)
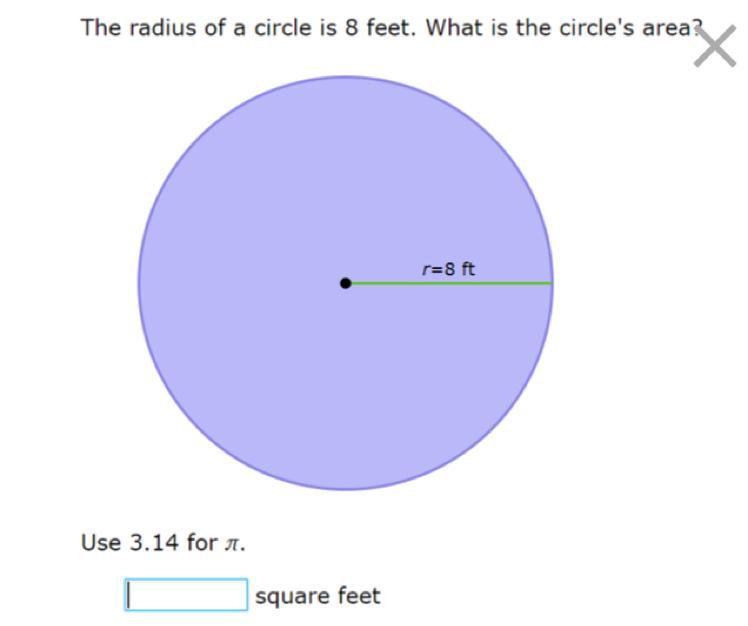
Answers
Answer:
A = 200.96 sq ft
Step-by-step explanation:
formula for area of a circle: A = π·r²
A = (3.14)·(8²)
A = 64·(3.14)
A = 200.96
Related Questions
Please help!!!!!!!!!!!!!!

Answers
therefore your answer is 8 cups
calculate the Geometric mean for the
distribution 8, 6, 3, 5 and 4
Answers
Answer:
Step-by-step explanation:
The geometric mean is the average of the 5 numbers
8 + 6 + 3 + 5 + 4 Just add.
Total = 26
There are 5 elements, so the average = 26/5 = 5.2
Draw a diagram of and of when x is 3.
Answers
How am I supposed to answer this question? I don't understand.
Answer:
Step-by-step explanation:
Here the graph :)

Gordon Miller's job shop has four work areas, A, B, C, and D. Distances in feet between centers of the work areas are: A B C D A − 5 9 7 B − − 6 8 C − − − 11 D − − − − Workpieces moved per week between work areas are: A B C D A − 900 900 500 B − − 500 200 C − − − 600 D − − − − It costs Gordon $22 to move 1 work piece 1 foot.What is the weekly total material handling cost of the layout?
Answers
Answer: $600,600
Step-by-step explanation:
Total handling cost :
Workpiece moved * cost * distance
Work area A :
-, (5 × 22 × 900), (9 × 22 × 900), (7 × 22 × 500)
-, 99000, 178200, 77000
Work area B:
-, -, (6 × 22 × 500), (8 × 22 × 200)
-, -, 66000, 35200
Work area C:
-, -, -, (11 × 22 × 600)
-,-,-, 145200
Work area D:
-, -, -, -
Total weekly handling cost :
(99000 + 178200 + 77000 + 66000 + 35200 + 145200)
= $600,600
Kindly check attached picture for more explanation

Billy walks 1/2 of a mile in 1/3 of an hour. What is Billy's walking speed?
A. 2/3
B. 3/2
C. 1/6
D. 6 mph
Answers
Answer: B
Step-by-step explanation:
multiply the 1/2 of a mile by 3 (to complete the full hour)
What is the volume of the solid?
Cheese yd
21.8 yd
19.2 yd
40.8 yd
please help!

Answers
Answer:
Step-by-step explanation:
Area of right triangular base = ½ × 3.2 × 6 = 9.6 square yards
Volume = 96 × 2 = 19.2 cubic yards
help
I need an answer

Answers
The correct option that indicates the quadrant that contains the translation of the shaded figure is the option B
B. III
What is a translation transformation?A translation is a transformation in which the size, relative position of the points on the pre-image, are preserved but the location of the pre-image changes to obtain the image.
The shape of the shaded figure is an L-shape
The geometric figure in quadrant II and IV are a reflection of the shaded figure, across the y-axis and across the x-axis, respectively which is not a translation transformation.
The geometric figure in quadrant III can be obtained from the shaded figure by a translation 4 units to the left and 5 units downwards, which can be expressed as <-4, -5>, which is a translation transformation, therefore;
The quadrant that contains a translation of the shaded figure is the quadrant IIILearn more on translation transformation here: https://brainly.com/question/11134096
#SPJ1
Write an equation describing the relationship of the given variables: y varies inversely as the cube root of x and when x=8, y=6
Answers
The equation describing the relationship between x and y is:
\(y = 12/x^{(1/3)}\)
A function's inverse function reverses the action of a function, or f.
If y varies inversely as the cube root of x, we can write the following equation:
\(y = k/x^{(1/3)}\)
If the corresponding elements of two sequences of numbers, frequently experimental data, have a constant ratio, known as the coefficient of proportionality or proportionality constant, then the two sequences of numbers are proportional or directly proportional.
where k is a constant of proportionality.
To solve for k, we can use the given information that when x=8, y=6:
\(6 = k/8^{(1/3)}\)
Simplifying the right side:
\(6 = k/2\\k = 12\)
Substituting k back into the equation, we get:
\(y = 12/x^{(1/3)}\)
Therefore, the equation describing the relationship between x and y is:
\(y = 12/x^{(1/3)}\)
for such more question on variables
https://brainly.com/question/28248724
#SPJ4
Two pedestrians simultaneously left two villages 27 km apart and walked toward each other, meeting after 3 hours. The first pedestrian walked at a speed of 4 km per hour. At what speed (in km per h) did the second pedestrian walk?
Answers
The speed of the second pedestrian is 5 kilometers per hour.
At what speed did the second pedestrian walk?Let's say that the speed of the second pedestrian is S.
We know that the other pedestrian walks at a speed of 4km/h, and they (together) travel a distance of 27km in 3 hours, then we can write the linear equation:
(4km/h + S)*3h = 27km
It says that both pedestrians work, together, a total of 27km in 3 hours.
Now we can solve that linear equation for S, to do this, we need to isolate S in the left side of the equation.
4km/h + S = 27km/3h = 9 km/h
S = 9km/h - 4km/h = 5km/h
The speed of the second pedestrian is 5 kilometers per hour.
If you want to learn more about speed:
https://brainly.com/question/4931057
#SPJ1
At Turtle Elementary, the kindergarten teachers lined up their students by 6s and there
were none left over. They lined them up again by 8s and there were none left over. They
tried to line them up again by 10s, but there were 2 left over. What is the least number
of students that could be in kindergarten at Turtle Elementary?
Answers
Answer:
Step-by-step explanation:
denote x as total students
lcm of 6 and 8 is 24 (so none left over)
keep trying becuz you wanna find the lowest possible number
48, 72
72 works.
amber has $300 in cash, $11,300 in investements and an automobile worth $13,400. She owes $3,900 on her auto los . What is her net worth?
Answers
Answer:
300+11300+13400-3900=21100
Step-by-step explanation:
GIVING 100 POINTS FOR THESE 3 PROBLEMS

Answers
Answer:
Step-by-step explanation:
\(A=\frac{a+b}{2}*h=\frac{4+7}{2}*3=16.5cm^2\)
\(A=\frac{ab}{2} =\frac{4*6}{2} =12in^2\)
\(A=wl=6*5=30in^2\)
\(12+30=42in^2\)
\(A=\frac{a+b}{2}h=\frac{28+40}{2}*30=1020ft^2\)
Wall = A=\(\frac{ab}{2} =\frac{6*30}{2}=90ft^2\)
Answer:
16.5cm²42in²90ft²Step-by-step explanation:
Question 1:
A = (a+b/2)h
A = (4+7/2)3
A = (11/2)3
A = (5.5)3
A = 16.5cm²
Question 2:
A = bh/2 = 6*4/2 = 24/2 = 12
A = bh = 6*5 = 30
A = 12 + 30 = 42
A = 42in²
Question 3:
A = (a+b/2)h
A = (28+40/2)30
A = (68/2)30
A = (34)30
A = 1020ft²
A = bh/2
A = 30*6/2
A = 180/2
A = 90ft²
Best of Luck!
Seven friends go to the local sandwich shop. All six people order the combination meal, which includes a drink and a veggie wrap for $4.95. One person thinks the total bill for all six friends will be around $20.00 Is that a reasonable estimate? Why? A. No, a reasonable estimate is around 6 times $7 = $42 B No, a reasonable estimate is around 5 times $6 = 30 C. No, a reasonable estimate is around 10 times $5 = 50 D Yes, a reasonable estimate is around 4 times $5 - $20 please help and don't just do for points
Answers
Answer: B
Step-by-step explanation:
$4.95 x 6 people = 29.7 ≈ $30
Answer:
utyfgkjnhm,b
Step-by-step explanation:
utgydfyr
the student government claims that 70% of all students favor an increase in student fees to buy indoor potted plants for the classrooms. a random sample of 12 students produced 2 in favor of the project.
(a) What is the probability that 2 or fewer in the sample will favor the project, assuming the student government's claim is correct? (Use 3 decimal places.) (b) Do the the data support the student government's claim, or does it seem that the percentage favoring the increase in fees is less than 70%? The data do not give us any indication that the percent favoring the increase in fees differs from 70%. The data seem to indicate that the percent favoring the increase in fees is greater than 70%. The data seem to indicate that the percent favoring the increase in fees is less than 70%. The data seem to indicate that the percent favoring the increase in fees is equal to 70%.
Answers
The probability that 2 or fewer in the sample will favor the project is 4.368 × 10⁻⁶ and Also The data seem to indicate that the percent favoring the increase in fees is less than 70%
According to the question,
It is given that according to the student's government
The probability that number of students in favor of increment in fees : p = 0.70
The probability that number of students against the increment : q = 0.30
Sample Size : n = 12
Number of students follows Binomial distribution
(a) We have to find the probability that 2 or fewer in the sample will favor the project
P( x ≤ 2) = P(0) + P(1) + P(2)
As we know ,
P(x) = ⁿCₓpˣq⁽ⁿ⁻ˣ⁾
=> P( x ≤ 2) = ¹²C₀p⁰q¹² + ¹²C₁p¹q¹¹ + ¹²C₂p²q¹⁰
=> P( x ≤ 2) = 1×(0.30)¹² + 12×(0.70)(0.30)¹¹ + 12×11/2 × (0.70)²(0.30)¹⁰
=> P( x ≤ 2) = (0.30)¹⁰ [ 0.09 + 0.21 + 0.48]
=> P( x ≤ 2) = 5.9×10⁻⁶[0.78]
=> P( x ≤ 2) = 4.368 × 10⁻⁶
Which is very close to zero
(b) The data doesn't support the student government claim.
The data seem to indicate that the percent favoring the increase in fees is less than 70%.
To know more about Binomial distribution here
https://brainly.com/question/29137961
#SPJ4
Nikhil and Mae work at the same company. Nikhil has been at the company 4 time+s as long as Mae. Nikhil's time at the company is 8 more than 2 times Mae's time. The following system of equations models the scenario: x = 4y x = 8 + 2y How many years has each person been employed by the company? Nikhil has been with the company for 16 years, while Mae has been there for 4 years. Nikhil has been with the company for 24 years, while Mae has been there for 6 years. Nikhil has been with the company for 20 years, while Mae has been there for 5 years. Nikhil has been with the company for 12 years, while Mae has been there for 3 years
Answers
Applying the system of equations given, we can conclude that: a. Nikhil has been with the company for 16 years, while Mae has been there for 4 years.
How to Apply a System of Equations?To solve the system of equations, let's substitute the value of x from the first equation into the second equation:
x = 4y
8 + 2y = 4y
Simplifying the equation, we get:
8 = 2y
Dividing both sides by 2:
4 = y
Now, substitute the value of y back into the first equation to find x:
x = 4y
x = 4(4)
x = 16
Therefore, Nikhil has been employed by the company for 16 years, and Mae has been employed for 4 years.
The correct answer is option a. Nikhil has been with the company for 16 years, while Mae has been there for 4 years.
Learn more about System of Equations on:
https://brainly.com/question/13729904
#SPJ1
Help Quickly! A truck needs 7 gallons of fuel to travel 56 miles. Can the truck travel 48 miles with 6 gallons of fuel? Explain.
Giving brainliest

Answers
Yes, 7/56 and 6/48 are proportional because 7×48 = 56×6. Therefore, the correct answer is option B.
Given that, a truck needs 7 gallons of fuel to travel 56 miles.
The truck travel 48 miles with 6 gallons of fuel.
Here, the proportion is
7:56::6:48
We know that, the proportion is product of extremes = product of means
7×48 = 56×6
336 = 336
Therefore, the correct answer is option B.
To learn more about the proportional relationship visit:
brainly.com/question/12917806.
#SPJ1
Solve for the unknown values
X = ?
Y = ?

Answers
Step-by-step explanation:
So 95 is a linear pair. a linear pair adds up to 180 so 180 - 95 = 85
X = 85
y = 50
anyone know the answer to this?

Answers
Answer:
0.99.Step-by-step explanation:
Remove the decimal point.
Then, divide.
I'll show you an image.

Two dice are rolled. Determine the probability of the following. ("Doubles" means both dice show the same number.)
Rolling an even number or doubles
Answers
The probability of the Doubles" means both dice show the same number is 36.
What is probability?When we don't know how an event will turn out, we can discuss the likelihood or likelihood of several outcomes. Statistics is the study of events that follow a probability distribution.
The probabilities of these two outcomes must be added in order to get the likelihood of rolling an even number or doubles, but since we have already tallied those outcomes twice, the probability of rolling both doubles and an even number must be subtracted. The probability of rolling doubles and an even number is 1/36 since rolling two sixes is the only method to get a double and an even number.
The likelihood of rolling an even number or doubles is thus:
The formula for P(even number or doubles) is P(even number) = P(even number) + P(doubles) - P(even number and doubles) = 1/2 + 1/6 - 1/36 = 19/36.
The odds of rolling an even number or two doubles are 19/36.
Therefore, the probability of the Doubles" means both dice show the same number is 36.
Learn more about probability, here:
https://brainly.com/question/30034780
#SPJ1
Need to find the expression that represents the width !

Answers
The given area is
\(A=x^3+4x^2-11x-30\)The length is
\(L=x^2-x-6\)Since the rule of the area ofthe rectangle is
\(A=L\times W\)Then to find the width, divide the area b the length
\(\begin{gathered} W=\frac{A}{L} \\ \\ W=\frac{x^3+4x^2-11x-30}{x^2-x-6} \end{gathered}\)We will just divide thefirst terms and thelst terms to find the answer
\(\begin{gathered} \frac{x^3}{x^2}=x \\ \frac{-30}{-6}=5 \end{gathered}\)Then the width is
\(W=x+5\)The answer is B
5x-3(-5y+6x) +4y i need help please
Answers
To simplify the expression \(\displaystyle\sf 5x-3(-5y+6x)+4y\), we can follow the order of operations, which involves simplifying the expressions within parentheses, applying the distributive property, and combining like terms.
Using \(\displaystyle\sf \) tags for formatting, the expression becomes:
\(\displaystyle\sf 5x-3(-5y+6x)+4y\)
First, we simplify the expression within the parentheses:
\(\displaystyle\sf 5x-3(-5y+6x)+4y\)
\(\displaystyle\sf 5x+15y-18x+4y\)
Next, we can combine the like terms:
\(\displaystyle\sf 5x-18x+15y+4y\)
\(\displaystyle\sf -13x+19y\)
Therefore, the simplified expression is \(\displaystyle\sf -13x+19y\).
\(\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}\)
♥️ \(\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}\)
Given that the following is a Rhombus, find the missing sides.

Answers
Answer:
AE = 6
AC = 12
BD = 16
AB = 10
Step-by-step explanation:
In a rhombus, which is equilateral, the diagonals bisect each other so,
AE = EC so 6
AC = AE + EC, which is 6+6
BD = ED + EB or 8+8
AB = BC so 10
Find the area of the figure shown below and choose the appropriate result.

Answers
Answer:
The answer is 39 cm squared
-5/6x =-10/3 solver for x
Answers
Answer:
X = 4
Step-by-step explanation:
Remove the fraction first by multiplying with 6 both sides.
Then leave the variable alone by diving with - 5
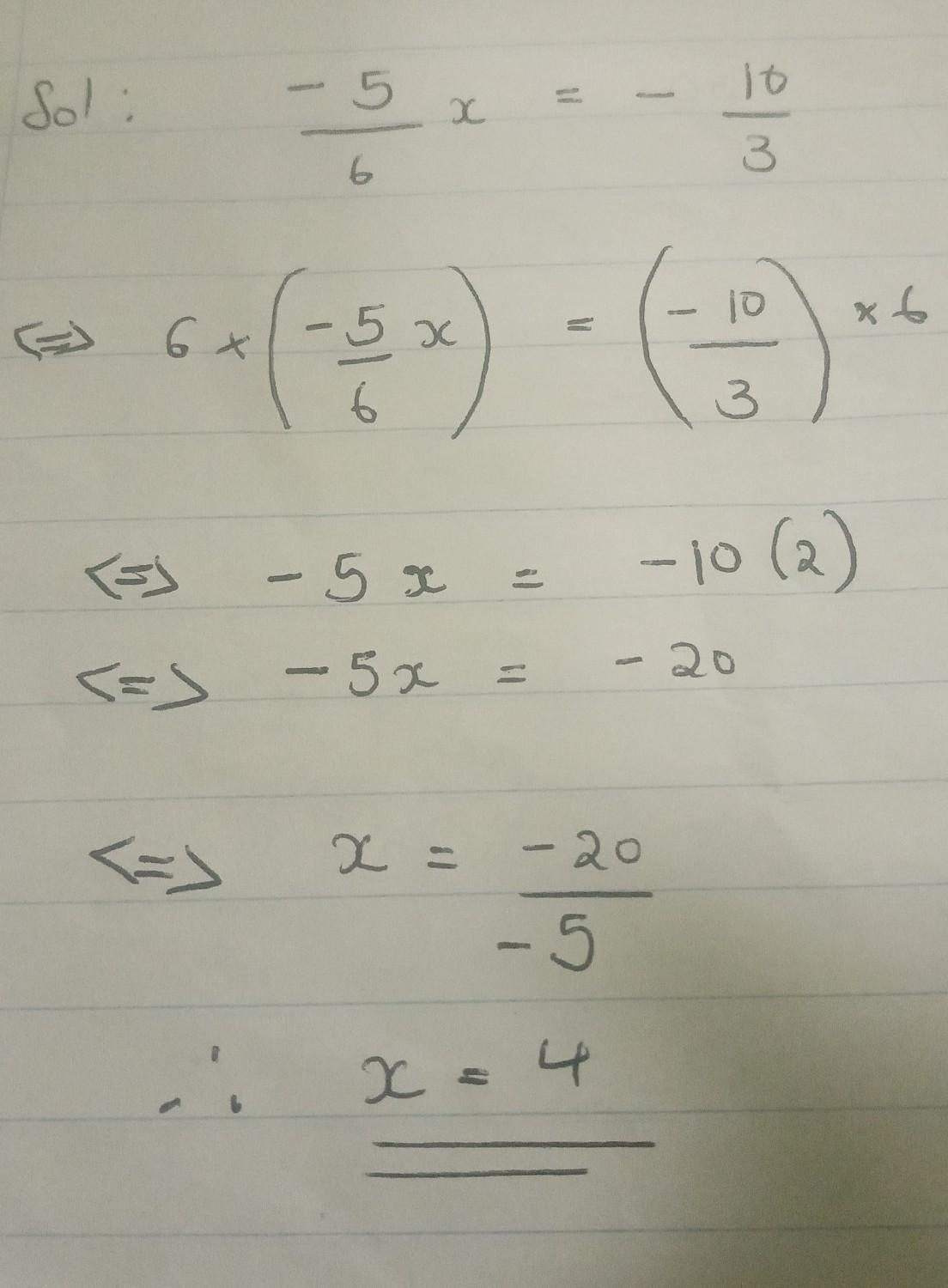
-------------------------------------------------------------------------------------------------------------
Answer: \(\textsf{x= 4}\)
-------------------------------------------------------------------------------------------------------------
Given: \(\textsf{-5/6x = -10/3}\)
Find: \(\textsf{The value of x}\)
Solution: In order to get the value of x we must multiply both sides by -6/5 to help cancel the coefficient on the left side to leave x by itself.
Multiply both sides by -6/5
\(\textsf{-5/6x * -6/5 = -10/3 * -6/5}\)\(\textsf{x = -10/3 * -6/5}\)\(\textsf{x = (-10 * -6)/(3 * 5)}\)Simplify the expression
\(\textsf{x= 60/15}\)\(\textsf{x= 4}\)Therefore, the value of the unknown variable x is 4.
What is the solution to the equation 4x + 2(x − 2) = 4x + x − 12? (1 point)
Question 13 options:
1)
−8
2)
−1
3)
1
4)
8
Answers
Answer:
It's -8
Step-by-step explanation:
DISTRIBUTE :
4x + 2( x - 2 ) = 4x + x - 12
4x + 2x - 4 = 4x + x - 12
COMBINE LIKE TERMS :
4x + 2x - 4 = 4x + x - 12
6x - 4 = 4x + x - 12
COMBINE LIKE TERMS :
6x - 4 = 4x + x - 12
6x - 4 = 5x - 12
ADD 4 TO BOTH SIDES :
6x - 4 = 5x - 12
6x - 4 + 4 = 5x - 12 + 4
ADD THE NUMBERS/ SIMPLIFY :
6x = 5x - 8
SUBTRACT 5x FROM BOTH SIDES :
6x = 5x - 8
6x - 5x = 5x - 8 - 5x
SIMPLIFY :
x = -8
What are the TERMS in the expression: 7x − 5y − x + 6
A: 7, 5 and 6
B: 7x, 5y, x, and 6
C: x, and y
Answers
Answer: B i think
Step-by-step explanation:
A term can be a number, a variable, product of two or more variables or product of a number and a variable. An algebraic expression is formed by a single term or by a group of terms.
-4|7 – 6k|= 14 solve for k

Answers
Answer:
no solution
Step-by-step explanation:
-4|7 – 6k| = 14
Divide both sides by -4.
|7 - 6k| = -14/4
|7 - 6k| = -7/2
An absolute value can never equal a negative number since an absolute value is always non-negative. Therefore, there is no solution.
Answer: no solution
Determine the number of solutions you will have for the system 4y + x = 16 and y = 4 – x.
Answers
Equaling both equations, it is found that the correct option that states the number of solutions you will have for the system is:
D: one solutionThe equations are:
\(4y + x = 16 \rightarrow x = 16 - 4y\)
\(y = 4 - x \rightarrow x = 4 - y\)
Equaling both equations for x, we have that:
\(16 - 4y = 4 - y\)
\(3y = 12\)
\(y = \frac{12}{3}\)
\(y = 4\)
\(x = 4 - y = 4 - y = 0\)
Hence, the system has one solution, which is (0,4), and option d is correct.
You can learn more about the number of solutions a system of equations has at https://brainly.com/question/25960609
Find the exact solutions of the given equation in the interval .
sin 4x= –2sin 2x

Answers
The exact solutions of the given equation in the interval are;
A: x = 0, π/2, π, ³/₂π
How to find the exact solutions of trigonometric equations?
We are given the equation as;
sin 4x = –2sin 2x
Writing the equation in standard form gives;
sin 4x + 2sin 2x = 0
Using trigonometric Identity, substitute (sin 4x) with (2sin 2x.cos 2x) to get;
2sin 2x cos 2x + 2sin 2x = 0
Factorize to get;
2sin 2x(cos 2x + 1) = 0
A. sin 2x = 0
The unit circle will give us 3 solutions for 2x as follows;
2x = 0
Thus; x = 0
2x = π
Thus; x = π/2
2x = 2π
Thus; x = π
B. cos 2x = - 1
The unit circle gives 2 solutions for 2x as;
2x = π
Thus; x = π/2
2x = 3π
Thus; x = ³/₂π
Read more about solutions of trigonometric equations at; https://brainly.com/question/28921050?source=archive
#SPJ1
Complete question is;
How do you find the exact solutions of the equation sin4x = −2sin2x in the interval [0, 2π)?
Solve for x. Round your answer to the nearest tenth.

Answers
The Pythagorean theorem should help you out. Since you already know two sides of the triangle, you can do a^2 + b^2 = c^2
So in this problem, 16.5^2 + 9.2^2 =
272.25 + 84.64 = 356.89
Pasty you would take the square root of 356.89 and you would get x = 18.89 or 18.9 rounded to the nearest tenth
You can check your work by the Pythagorean theorem once more. 16.5^2 + 9.2^2 = 18.9^2 and you should get the same approximate answer (it will be a little bigger because you rounded)