an ice cream company is going to open new stores in los angeles, chicago, and new orleans. the monthly cost for a square foot .find the total monthyl rent for all three stores.find the total monthyl rent for of rental space in each city was follows. los angeles $5.25, chicago $6.95 and new orleans $4.25. the store in los angels will be 560 square , chicago will be 330 square feet and new orleans will be 495 square feet.
Answers
The total monthly rent for these three stores is $8,786.25.
What is total ?
Total refers to an entire or complete amount, and the verb "to total" means to combine two numbers or to destroy anything. In mathematics, you add integers to get the total; the outcome is the total. The result of adding 8 and 8 is 16.
The outcome of adding two or more numbers or phrases is known as the sum in mathematics. The sum is a method of bringing things together as a result. To put it another way, adding two or more numbers together results in a new result or total.
The monthly cost for a square foot of rental space in each city is as follows:
Place Monthly Cost for a Square Foot
Los Angeles $5.75
San Francisco $6.95
Seattle $4.25
It is also provided that the store in Los Angeles will be 580 square feet, the store in San Francisco will be 500 square feet, and the store in Seattle will be 465 square feet.
Compute the total monthly rent for these three stores as follows:
Total Monthly Rent = Monthly Cost for a Square Foot × Area
= (5.75 * 580) +(6.95 * 500) +(4.25 * 465)
= 3335 + 3475 + 1976.25
= 8786.25
Thus, the total monthly rent for these three stores is $8,786.25.
To learn more about total from the given link
https://brainly.com/question/18798695
#SPJ1
Related Questions
. Joaquin played basketball with his friends from 1:10 to 3:35. He arrived home 20 minutes later. How many minutes passed from the time Joaquin started playing basketball until the time he arrived at home?
Answers
Answer:
165 minutes
Step-by-step explanation:
To solve for the number of minutes that Joaquin played for, we can use this expression:
(let 'a' represent how much time passed from the time Joaquin started playing basketball until the time he arrived at home)
1:10 + a = 3:35Subtracting 1:10 from each side:
1:10 - 1:10 + a = 3:35 - 1:101:10 - 1:10 cancels out to 0, while 3:35 - 1:10 is equal to 2:25.
So, the expression is now:
a = 2:25So, 2 hours and 25 minutes passed.
If we know that 1 hour is equivalent to 60 minutes, we can use this expression to solve for however many minutes are in 2 hours:
2 × 60 = 120Now we need to add on the number of minutes and the time it took him to get home:
120 + 25 + 20 = 165Therefore, 165 minutes passed from the time Joaquin started playing basketball until the time he arrived at home.
A convex lens with focal length f centimeters will project the image of an object on a
point behind the lens. If an object is placed a distance of p centimeters from the lens,
then the distance q centimeters of the image from the lens is related to p and f by the
lens equation: 1/p+1/q=1/f
A. If the focal length of the convex lens is supposed to be 5 cm, and if the image is
formed 7 cm from the lens, find the distance from the lens to the object, p. (It’s not necessary to simplify your answer.)
B. Find an expression that gives q as a function of p, assuming that the focal length is a constant of 5 centimeters.
C. Sketch a graph of q as a function of p (i.e., q(p)), assuming that the focal length is a
constant of 5 centimeters. Show any important features of the graph.
D. Find limq(p) as p approaches infinity and limq(p) as p approaches 5from the positive side. What do these limits represent physically? What must
happen to the distance of the image and the object?
Answers
Answer:
A. Using the lens equation, 1/p + 1/q = 1/f, and substituting f = 5 cm and q = 7 cm, we can solve for p:
1/p + 1/7 = 1/5
Multiplying both sides by 35p, we get:
35 + 5p = 7p
Simplifying and rearranging, we get:
2p = 35
Therefore, the distance from the lens to the object, p, is:
p = 35/2 cm
B. Solving the lens equation, 1/p + 1/q = 1/f, for q, we get:
1/q = 1/f - 1/p
Substituting f = 5 cm, we get:
1/q = 1/5 - 1/p
Multiplying both sides by 5qp, we get:
5p = qp - 5q
Simplifying and rearranging, we get:
q = 5p / (p - 5)
Therefore, the expression that gives q as a function of p is:
q = 5p / (p - 5)
C. Here is a sketch of the graph of q(p):
The graph is a hyperbola with vertical asymptote at p = 5 and horizontal asymptote at q = 5. The image distance q is positive for object distances p greater than 5, which corresponds to a real image. The image distance q is negative for object distances p less than 5, which corresponds to a virtual image.
D. Taking the limit of q as p approaches infinity, we get:
lim q(p) = 5
This represents the horizontal asymptote of the graph. As the object distance becomes very large, the image distance approaches the focal length of the lens, which is 5 cm.
Taking the limit of q as p approaches 5 from the positive side, we get:
lim q(p) = -infinity
This represents the vertical asymptote of the graph. As the object distance approaches the focal length of the lens, the image distance becomes infinitely large, indicating that the lens is no longer able to form a real image.
In order for the lens to form a real image, the object distance p must be greater than the focal length f. When the object distance is less than the focal length, the lens forms a virtual image.
what is 2x to the power of 2
helpppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppp
Answers
Answer:
2x^2 = (2 x 2) x (2 x 2)
= 4 x 4
= 16
I hope this helps you
list the angles in order from smallest to largest. show your work.

Answers
Answer:
∠R, ∠P, ∠QStep-by-step explanation:
The greater side has greater angle opposite
Sides in ascending order:
17, 21, 26Angles in ascending order:
∠R, ∠P, ∠QAt time T equals zero, water begins to drip out of the pipe into an empty bucket. After 42 minutes, there are 6 inches of water in the bucket. Right Ellen air function rule to model how many inches of water W are in the bucket after any number of minutes T.
Answers
the values of 'm' and 'b' are 0.5 and 0 respectively.
Step-by-step explanation:
A marketing firm conducts a survey to determine the ages of their survey subjects who like a new health drink.
This is the resulting data from their survey:
49, 63, 78, 22, 41, 39, 75, 61, 63, 65,
58. 37. 45, 52, 81, 75, 78, 72, 68, 59,
72, 85, 63, 61, 75, 39, 41, 48, 59,55
61, 25, 61, 52, 58, 71, 75, 82, 49, 51
The mean age of the subjects who like the new health drink is (type your answer...)
and the median age of the subjects is (type your answer..)
Answers
Answer:
Mean = 59.1, Median = 61
(there might have been a mistake in calculation (a lot of numbers!))
Step-by-step explanation:
The sample size is 40,
Now, the formula for the mean is,
Mean = (sum of the sample values)/(sample size)
so we get,
\(Mean = (49+63+78+22+41+39+75+61+63+65+58+37+45+52+81+75+78+72+68+59+72+85+63+61+75+39+41+48+59+55+61+25+61+52+58+71+75+82+49+51)/40\\Mean = 2364/40\\Mean = 59.1\)
To find the median, we have to sort the list in ascending (or descending)order,
we get the list,
22,25,37,39,39,41,41,45,48,49,
49,51,52, 52,55,58, 58, 59, 59, 61,
61, 61, 61, 63, 63, 63, 65, 68, 71, 72,
72, 75, 75, 75, 75, 78, 78, 81, 82, 85
Now, we have to find the median,
since there are 40 values, we divide by 2 to get, 40/2 = 20
now, to find the median, we takethe average of the values above and below this value,
\(Median = ((n/2+1)th \ value + (n/2)th \ value )/2\\where, \ the\ (n/2)th \ value \ is,\\n/2 = (total \ number \ of \ samples) /2\\n/2=40/2\\(n/2)th = 20\\Hence\ the (n/2)th \ value \ is \ the \ 20th \ value\)
And the (n+1)th value is the 21st value
Now,
The ((n/2)+1)th value is 61 and the nth value is 61, so the median is,
Median = (61+61)/2
Median = 61
The selling price of a ring is $900. This represents $150 less than three times the cost of the ring. Find the cost of the ring.
Answers
3x=1050
x=350
Helppp meee Pleaseee

Answers
Answer:
4
Step-by-step explanation:
I like to use the FOIL method! I've attached a quick picture of how it works below, but basically you multiply the first terms. Next, multiply the outside/outer terms. Then, multiply the inside/inner terms. Lastly, you multiply the last terms.
In this question, the binomial is (x + 2)².
You can expand this to be (x + 2)(x + 2).
When you expand it using the FOIL method, you get x times x, which is x².
Next, the outside/outer terms are x and 2, which is 2x.
Then, you multiply the inside/inner terms 2 and x, which is 2x.
Last, you multiply the last terms, which are 2 and 2, which is 4.
When you put them together, it looks like this:
x² + 2x + 2x + 4.
You can simplify this to x² + 4x + 4.
So your answer is 4.

One angle measures 18°, and another angle measures (6d − 6)°. If the angles are complementary, what is the value of d? d = 2 d = 13 d = 31 d = 36.2
Answers
The value of d for the given angles will be equal to d = 13. The correct option is B.
What is the complementary angle?The angle is defined as the span between two intersecting lines or surfaces at or close to the point where they meet.
Complementary angles are formed when the sum of two angles equals 90 degrees. 30 degrees and 60 degrees, for example, are complementary angles.
Given that one angle measures 18° and another angle measures (6d − 6)°.
The value of d will be calculated as,
18 + 6d - 6 = 90
6d + 12 = 90
6d = 90 - 18
6d = 78
d = 78 / 6
d = 13
To know more about complementary angles follow
https://brainly.com/question/20728641
#SPJ1
Plot the points (-6,8)(−6,8)left parenthesis, minus, 6, comma, 8, right parenthesis and (0,8)(0,8)left parenthesis, 0, comma, 8, right parenthesis on the coordinate plane below.
Answers
Answer:
hello I cant help you right now try again later
what is the quotient? can someone please help.

Answers
Answer:
-3
Step-by-step explanation:
hope this helps
An industrial machine made 9,096 cans of diet soda and 5times as many regular soda over the course of 53 minutes.Then the regular soda were placed into 2shipping boxes with each shipping box containing the same number of soda. How many regular sodas were in each shipping box?
Answers
Using proportions, it is found that 22,740 regular sodas were in each shipping box.
What is a proportion?A proportion is a fraction of a total amount.
We have that the number of regular soda cans is 5 times 9,096, hence:
R = 5 x 9,096 = 45,480.
Each of the two boxes contain the same number of sodas, hence:
N = 45,480/2 = 22,740.
22,740 regular sodas were in each shipping box.
More can be learned about proportions at https://brainly.com/question/24372153
2 pounds 6 ounces = ounces
Answers
2 pounds 6 ounces in ounces is equivalent to 38 ounces.
The given measurement is -
2 pounds 6 ounces
In 1 pound, there are 16 ounces.
So, we can write that -
2 pounds 6 ounces = 2 x 16 + 6
2 pounds 6 ounces = 38 ounces
So, 2 pounds 6 ounces in ounces is equivalent to 38 ounces.
To solve more questions on unit conversion, visit the link-
brainly.com/question/11805053
#SPJ1
Given the geometric sequence an with the following information, find a7.

Answers
To find the value of Az in the geometric sequence, we can use the given information. The geometric sequence is represented as follows: A3, 60, 160, 06 = 9.
From this, we can see that the third term (A3) is 60 and the common ratio (r) is 160/60.
To find Az, we need to determine the value of the nth term in the sequence. In this case, we are looking for the term with the value 9.
We can use the formula for the nth term of a geometric sequence:
An = A1 * r^(n-1)
In this formula, An represents the nth term, A1 is the first term, r is the common ratio, and n is the position of the term we are trying to find.
Since we know A3 and the common ratio, we can substitute these values into the formula:
60 =\(A1 * (160/60)^(3-1)\)
Simplifying this equation, we have:
\(60 = A1 * (8/3)^260 = A1 * (64/9)\)
To isolate A1, we divide both sides of the equation by (64/9):
A1 = 60 / (64/9)
Simplifying further, we have:
A1 = 540/64 = 67.5/8.
Therefore, the first term of the sequence (A1) is 67.5/8.
Now that we know A1 and the common ratio, we can find Az using the formula:
Az = A1 * r^(z-1)
Substituting the values, we have:
Az =\((67.5/8) * (160/60)^(z-1)\)
However, we now have the formula to calculate it once we know the position z in the sequence.
For more such questions on geometric sequence
https://brainly.com/question/24643676
#SPJ8
evaluate the following polynomial when x = - 3
+6x² – 3x+5
2x
Answers
Answer:
-93
Step-by-step explanation:
Substitute by - 3 instead of X
Determine whether the given value is a statistic or a parameter. A study was conducted of all 1575 workers in a certain state.
Answers
Answer:
Step-by-step explanation:
Consider the following functions. f=[(-1,1),(1,-2),(3,-4) and g=[(5,0),(-3,4),(1,1),(-4,1)} Find (f-g)(1) =
Answers
The difference between the functions give:
(f - g)(1) = f(1) - g(1) = -3
How to find the difference between the functions?
For two functions f(x) and g(x), the difference is defined as:
(f - g)(x) = f(x) - g(x).
Then:
(f - g)(1) = f(1) - g(1)
By looking at the given tables, we know that:
f(1) = -2
g(1) = 1
Replacing that we get:
(f - g)(1) = f(1) - g(1) = -2 - 1 = -3
If you want to learn more about difference of functions:
https://brainly.com/question/17431959
#SPJ1
The number of calories burned by a 90-pound cyclist is proportional to the number of hours the cyclist rides. The equation to represent this relationship is y = 225x. What is the constant of proportionality?
A:135
B:225
C:315
D:90

Answers
Answer:
The constant of proportionality is 225
Step-by-step explanation:
Given
\(y = 225x\)
Required
Determine the constant of proportionality (k)
A direct proportion is represented as:
\(y = kx\)
Where k is the constant of proportionality
By comparing:
\(y = kx\) to \(y = 225x\)
Hence:
\(k = 225\)
Graph the function
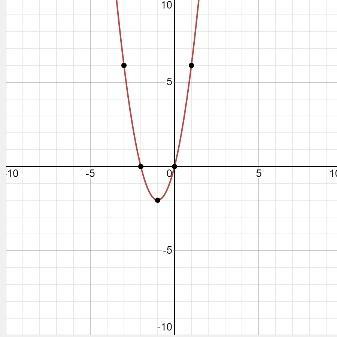
y = 2x^2+4x
Answers
Answer:
Hey!
Step-by-step explanation:
Hope this helps you!
Best of luck! <3

what is a 2 step equation equivalent to 12?
Answers
Answer:
\(\sqrt{x-3} = 3\)
Step-by-step explanation:
A 12 cm by 12 cm square piece of paper has 5 holes punched out of it. 4 of the holes are circles of radius 3 cm and 1 of the holes is a circle of radius 1 cm. The paper and punched holes can be visually interpreted as below. Determine the area of paper remaining after the holes have been punched out.

Answers
5 holes have been punched into a 12 cm by 12 cm square piece of paper. The area of remaining paper will be 27.714 cm².
Firstly, we will calculate the area of the square of paper in which the holes are punched.
Side of square = 12 cm
Area of square = side²
= (12) ²
= 144 cm²
Now, we will calculate the area of the bigger punch holes
Radius of big punch hole = 3 cm
Area of 1 big punch = π (radius) ²
= 22/7 × (3)²
22 / 7 × 9
= 198 / 7 cm²
Area of 4 punches = 4 × 198/7
= 792/7 cm²
Now, we will calculate the area of smaller punch whose radius is 1cm
Area = 22/7 × 1²
= 22/7 cm²
Now, we will calculate the total area covered by circles
Total area covered by circles = area of small punch + area of 4 big punch
= 22/7 + 792/7
= 814 /7 cm²
Remaining area = area of square - area of circles
= 144 - 814/7
= (1008 - 814) / 7
= 194 / 7
= 27.714 cm²
To know more about area:
https://brainly.com/question/27683633
#SPJ1
I'm stuck on this!!can someone pls help me

Answers
Step-by-step explanation:
i and iii are correct. you are supposed to substitute and find the correct value

the Pythagorean theorem
please help answer all the questions

Answers
Answer:
Step-by-step explanation:
A.)
\(a^{2} + b^{2} = c^{2}\)
\(16^{2} +20^{2}= c^{2}\)
256 + 400 = \(c^{2}\)
656 = \(c^{2}\)
25.6 = c
__________________________________________________________
B.)
\(a^{2} + b^{2} = c^{2}\)
\(25^{2}+ 10^{2} = c^{2}\)
625 + 100 = \(c^{2}\)
725 = \(c^{2}\)
26.9 = c
__________________________________________________________
C.)
\(a^{2} + b^{2} = c^{2}\)
\(12^{2} +10^{2}= c^{2}\)
144 + 100 = \(c^{2}\)
244 = \(c^{2}\)
15.6 = c
__________________________________________________________
D.)
\(a^{2} + b^{2} = c^{2}\)
\(26^{2}+ 24^{2} =c^{2}\)
676 + 576 = \(c^{2}\)
1,252 = \(c^{2}\)
35.4
__________________________________________________________
Sry it takes a lot of time to put in these equations and all that
Hope it helped!
This figure consists of a rectangle and a quarter circle.
What is the perimeter of this figure?
Use 3.14 for π.
Enter your answer as a decimal in the box.
cm

Answers
Answer:
75.27
Step-by-step explanation:
Rectangle = 20+2+2+20-11=47
quarter circle = 1/4(2)(11)(3.14)=17.27 + 11 = 28.27
47+28.27=75.27
Answer:
75.27.cm
Step-by-step explanation:
it works i got a 100 on the test
its Distributive Property please help lol..

Answers
Answer:
d= -4
Step-by-step explanation:
First you multiply the 3 by 6. You don't multiply the Coefficient with the variable.
(6x3)+5d = -2
Then you'll get: 18 + 5d = -2
At this point you just subtract from both sides
18 + 5d= -2
-18 -18
This becomes 5d = -20
\(\frac{5d}{5}\) =\(\frac{-20}{5}\)
-20/5 equals -4.
Answer:
I believe your answer will be d = -2/3
Step-by-step explanation:
hope it helps! (sorry im late- cough-)
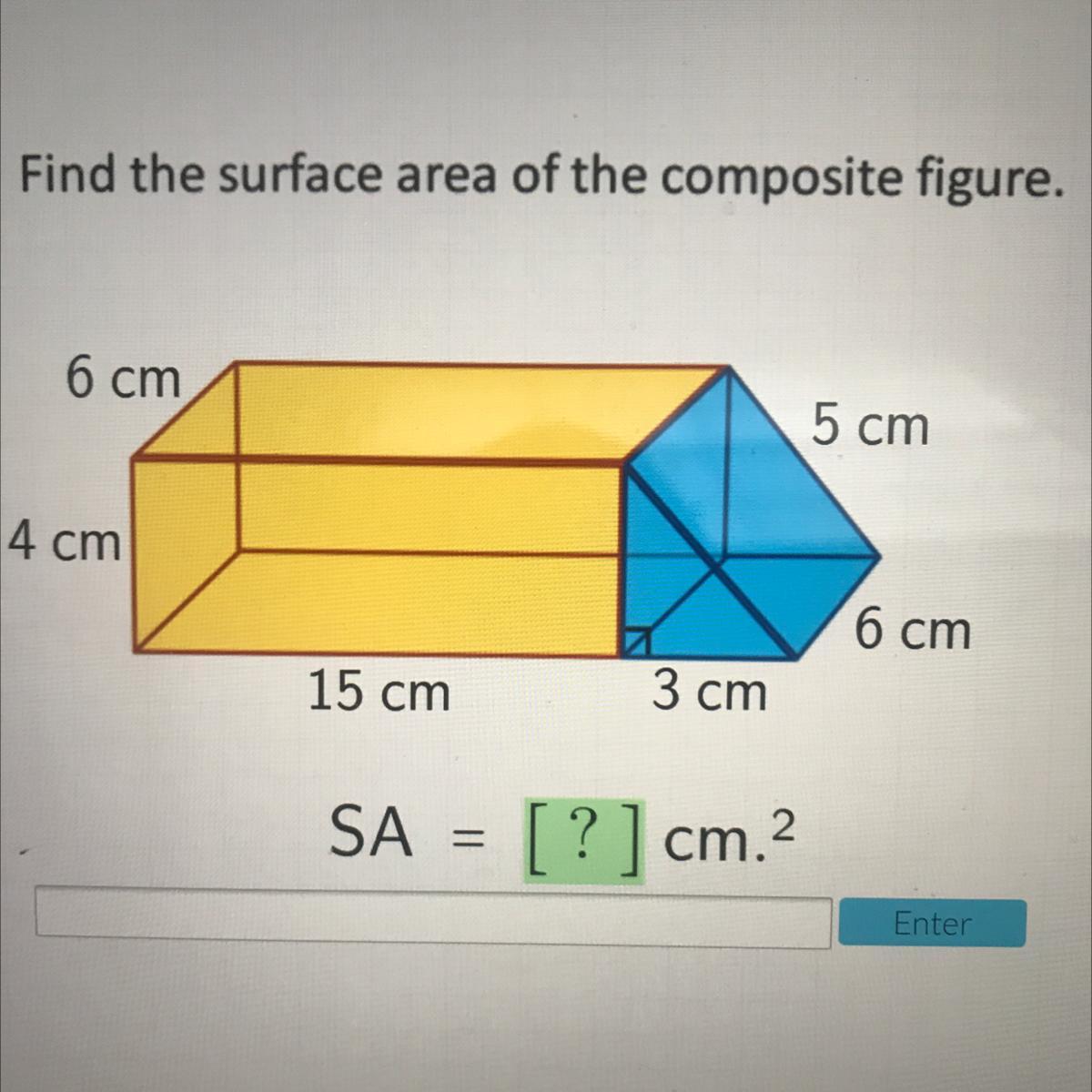
Find the surface area of the composite figure.
6 cm
5 cm
4 cm
6 cm
15 cm
3 cm
Answers
The surface area of the given composite figure will be 384 square cm.
What is surface area?The space occupied by any two-dimensional figure in a plane is called the area. The area of the outer surface of any body is called the surface area.
In the given image we have a composite figure one is a rectangular cuboid and the other is a triangular prism. The surface area will be equal to the sum of all the outer sides of the figure.
The surface area of the triangular shape will be calculated as:-
SA = 2( Area of triangle ) + Area of rectangular surfaces
SA = 2 ( (1/2) B x H ) + (5 x 6 ) + ( 6 x 3 )
SA = ( 3 x 4 ) + ( 30 ) + ( 18 )
SA = 12 + 30 + 18
SA = 60 square cm
The surface area of the rectangular cuboid will be calculated as:-
SA = ( 4 x 6 ) + 2 ( 158 x 4 ) + 2 ( 15 X 6 )
SA = 24 + 120 + 180
SA = 324 square cm
Total surface area will be = 324 + 60 = 384 square cm.
Therefore the surface area of the given composite figure will be 384 square cm.
To know more about a surface area follow
https://brainly.com/question/25292087
#SPJ1
Alex and Morgan or ask to solve 2x-5=5x+7+3x X equal 5
Answers
Answer:
no solution?
Step-by-step explanation:
2(5)-5=5(5)+7+3(5) <-- plug in 5
10−5=25+7+15
5=32+15
5=47
What is the length of AC

Answers
Answer:
5.8
Step-by-step explanation:
The angle bisector makes the triangle sides on either side of it proportional.
AC/CD = AB/BD
AC = CD·AB/BD
AC = 2(8.1/2.8) = 8.1/1.4 ≈ 5.7857 . . . . substitute shown values, evaluate
AC ≈ 5.8
Swornima is an unmarried nurse in a
hospital. Her monthly basic salary is Rs
48,000. She has to pay 1% social
security tax on her income up to Rs
5,00,000 and 10% income tax on Rs
5,00,001 to Rs 7,00.000. She gets 1
months' salary as the Dashain
allowance. She deposits 10% of her
basic salary in Citizen Investment Trust
(CIT) and gets 10% rebate on her
income tax. Answer the following
questions. (i) What is her annual
income? How much tax is rebated to
her? (iii) How much annual income tax
should she pay?
Answers
To calculate Swornima's annual income and the amount of tax she should pay, let's break down the information provided:
Monthly basic salary: Rs 48,000
Social security tax rate: 1%
Income tax rate on income up to Rs 5,00,000: 0% (no tax)
Income tax rate on income from Rs 5,00,001 to Rs 7,00,000: 10%
Dashain allowance: 1 month's salary
Deposit in Citizen Investment Trust (CIT): 10%
Rebate on income tax: 10%
(i) Annual Income:
Swornima's monthly basic salary is Rs 48,000, so her annual basic salary would be:
Annual Basic Salary = Monthly Basic Salary x 12
= Rs 48,000 x 12
= Rs 5,76,000
Additionally, she receives 1 month's salary as the Dashain allowance, which we can add to her annual income:
Annual Income = Annual Basic Salary + Dashain Allowance
= Rs 5,76,000 + Rs 48,000
= Rs 6,24,000
Swornima's annual income is Rs 6,24,000.
(ii) Tax Rebate:
Swornima receives a 10% rebate on her income tax. To calculate the rebate, we need to determine her income tax first.
(iii) Annual Income Tax:
First, let's calculate the income tax for the range of income from Rs 5,00,001 to Rs 7,00,000. The tax rate for this range is 10%.
Taxable Income in this range = Rs 6,24,000 - Rs 5,00,000
= Rs 1,24,000
Income Tax in this range = Taxable Income x Tax Rate
= Rs 1,24,000 x 0.1
= Rs 12,400
Now, let's calculate the total annual income tax:
Total Annual Income Tax = Income Tax in the range Rs 5,00,001 to Rs 7,00,000
= Rs 12,400
Next, we calculate the rebate on income tax:
Tax Rebate = Total Annual Income Tax x Rebate Rate
= Rs 12,400 x 0.1
= Rs 1,240
Swornima's annual income tax is Rs 12,400, and she receives a tax rebate of Rs 1,240.
To summarize:
(i) Swornima's annual income is Rs 6,24,000.
(ii) Swornima's tax rebate is Rs 1,240.
(iii) Swornima should pay an annual income tax of R
Use the Chain Rule to find ∂z/∂s and ∂z/∂t. (Enter your answer only in terms of s and t. Please use * for multiplication between all factors.)\(z = x^{7}y^{7}, x = s cos(t), y = s sin(t)\)
Answers
Applying the Chain Rule, the derivatives are given as follows:
\(\frac{\partial z}{\partial s} = 7(s\cos{t})^6(s\sin(t))^6(y\cos{t} + x\sin{t})\)\(\frac{\partial z}{\partial t} = 7s(s\cos{t})^6(s\sin{t})^6(-y\sin{t} + x\cos{t})\)What is the derivative of Z as a function of s?
The function Z is defined as follows:
z = x^7y^7.
The variables x and y are functions of variables s and t, as follows:
x = s cos(t).y = s sin(t).Hence the derivative of z as a function of s is given as follows:
∂z/∂s = (dz/dx)(dx/ds) + (dz/dy)(dy/ds).
Hence, applying the derivative rules for the exponents, and for the exponents, we have that:
\(\frac{\partial z}{\partial s} = 7x^6y^7\cos{(t)} + 7y^6x^7\sin{(t)} = 7x^6y^6(y\cos{t} + x\sin{t})\)
Replacing the values of x and y, we have that:
\(\frac{\partial z}{\partial s} = 7(s\cos{t})^6(s\sin(t))^6(y\cos{t} + x\sin{t})\)
What is the derivative of Z as a function of t?We follow the same logic as above, only that now the inside derivatives, that is, the derivatives of x and y, are as function of t and not of s, hence:
∂z/∂t = (dz/dx)(dx/dt) + (dz/dy)(dy/dt).
Then:
\(\frac{\partial z}{\partial t} = -7x^6y^7s\sin{(t)} + 7y^6x^7s\cos{(t)} = 7sx^6y^6(-y\sin{t} + x\cos{t})\)
Then, replacing x and y as functions of s and t, we have that:
\(\frac{\partial z}{\partial t} = -7x^6y^7s\sin{(t)} + 7y^6x^7s\cos{(t)} = 7s(s\cos{t})^6(s\sin{t})^6(-y\sin{t} + x\cos{t})\)
More can be learned about the Chain Rule at https://brainly.com/question/26731132
#SPJ1