An engineering study indicates that 8.5% of the bridges in a large state are structurally deficient. The state's department of transportation randomly samples 100 bridges. What is the probability that exactly 6 bridges in the sample are structurally deficient
Answers
Answer:
\(P(X=6)=(100C6)(0.085)^6 (1-0.085)^{100-6}=0.1063\)
Then the probability that exactly 6 bridges in the sample are structurally deficient is 0.1063 or 10.63%
Step-by-step explanation:
Let X the random variable of interest "number of bridges in the sample are structurally deficient", on this case we now that:
\(X \sim Binom(n=100, p=0.085)\)
The probability mass function for the Binomial distribution is given as:
\(P(X)=(nCx)(p)^x (1-p)^{n-x}\)
Where (nCx) means combinatory and it's given by this formula:
\(nCx=\frac{n!}{(n-x)! x!}\)
And we want to find this probability:
\( P(X=6)\)
And if we use the probability mass function and we replace we got:
\(P(X=6)=(100C6)(0.085)^6 (1-0.085)^{100-6}=0.1063\)
Then the probability that exactly 6 bridges in the sample are structurally deficient is 0.1063 or 10.63%
Related Questions
MC1103: A travel agent books passages on three different tours, with half of her customers choosing tour T1, one-third choosing tour T2, and the remaining one-sixth choosing tour T3. The agent has noted that 3/4 of those who take T1 return to book passage again, 2/3 of those who take T2 return, and 1/2 of those who take T3 return. If a customer does return, what is the probability that the person first went on tour T2
Answers
Using conditional probability, it is found that there is a 0.3266 = 32.66% probability that the person first went on tour T2.
Conditional Probability
\(P(B|A) = \frac{P(A \cap B)}{P(A)}\)
In which
P(B|A) is the probability of event B happening, given that A happened. \(P(A \cap B)\) is the probability of both A and B happening. P(A) is the probability of A happening.In this problem:
Event A: Customer returns.Event B: Customer first went on tour T2.The percentages associated with a return are:
3/4 = 0.75 of 0.5(choosing T1).2/3 = 0.6667 of 1/3 = 0.3333(choosing T2).1/2 = 0.5 of 1/6 = 0.1667(choosing T3).Hence:
\(P(A) = 0.75(0.5) + 0.667(0.3333) + 0.5(0.1667) = 0.6806611\)
The probability of both returning and first going on T2 is:
\(P(A \cap B) = 0.667(0.3333)\)
Hence, the conditional probability is:
\(P(B|A) = \frac{P(A \cap B)}{P(A)} = \frac{0.667(0.3333)}{0.6806611} = 0.3266\)
0.3266 = 32.66% probability that the person first went on tour T2.
A similar problem is given at https://brainly.com/question/14398287
100 PTS AND BRAINLIEST WRONG ANSWERS REPORTED
The function p(w)=230(1.1)^W represents the number of specialty items produced at the old factory w
weeks after a change in management. The graph represents the number of specialty items produced at the
new factory during the same time period.
(a) During Week 0, how many more specialty items were produced at the old factory than at the new
factory? Explain.
(b) Find and compare the growth rates in the weekly number of specialty items produced at each factory.
Show your work.

Answers
Answer:
40; 0.1 and 0.16
Step-by-step explanation:
a. We know that p(w)=230(1.1)^W represents the number of specialty items produced at the old factory.
This equation is in the form of an exponential growth function:
f(x)=a(1+r)^x
where a is the initial value, r is the growth rate, and x is the number of time intervals.
That means that for p(w)=230(1.1)^W:
230 is the initial value, and 0.1 is the growth rate. (1.1-1)
Therefore, for week 0, there were 230 specialty items produced at the old factory.
We can also plug in 0 for w (0 time intervals) to get the same answer
That would look like:
p(0)=230(1.1)^0
p(0)=230(1)
p(0)=230
On the other hand, for the new factory, if you go find 0 on the x-axis, you'll notice that 190 specialty items were produced in week 0.
230-190=40
This means that our answer for a is that 40 more specialty items were produced at the old factory than the new factory.
_____
b. Our first step for this question would be to find the equation for the graph.
We can immediately recognize that this is an exponential growth function, similar to the other equation.
As a reminder, exponential growth functions are in the form: f(x)=a(1+r)^x
We can put it in terms of production and weeks:
p(w)=a(1+r)^w
We know that the initial value is 190 by the graph.
p(w)=190(1+r)^w
Now we just need to find the growth rate:
We can do this by choosing a value (other than the first point) and plugging it in. Let's use (1, 220) which is in the form (w, p)
Plug it in to the equation:
220=190(1+r)^1
220=190(1+r)
Distribute
220=190+190r
Subtract 190 from both sides
30=190r
Divide 190 from both sides
r=0.1578947368 (round how your teacher asks)
Next, all we have to do is find the growth rate for the old factory:
p(w)=230(1.1)^W
1.1=1+r
Therefore, r=0.1
The growth rate at the old factory is 0.1.
When comparing them, we'll realize that the growth rate at the new factory is about 0.06 higher.
#1
For old factory
p(w)=230(1.1)^wSo
week =0\(\\ \rm\dashrightarrow p(0)=230(1.1)^0=230(1)=230\)
For nEW factory
On graph y intercept is 190Difference:-
230-190=4040 items were more produced
#2
For old factory
Turn it to p(1+r)^t form where r is rate of change\(\\ \rm\dashrightarrow 230(1+0.1)^t\)
Growth rate is 0.1For new factory
(0,190)(1,220)Find slope:-
\(\\ \rm\dashrightarrow m=\dfrac{220-190}{1}=30\)
Find growth rate
m/b(b is y intercept)30/1903/190.16New factory has greater growth rate
Determine if the two triangles are congruent. If they are, state how you know.
A.
AAS
B.
ASA
C.
SSS
D.
SAS
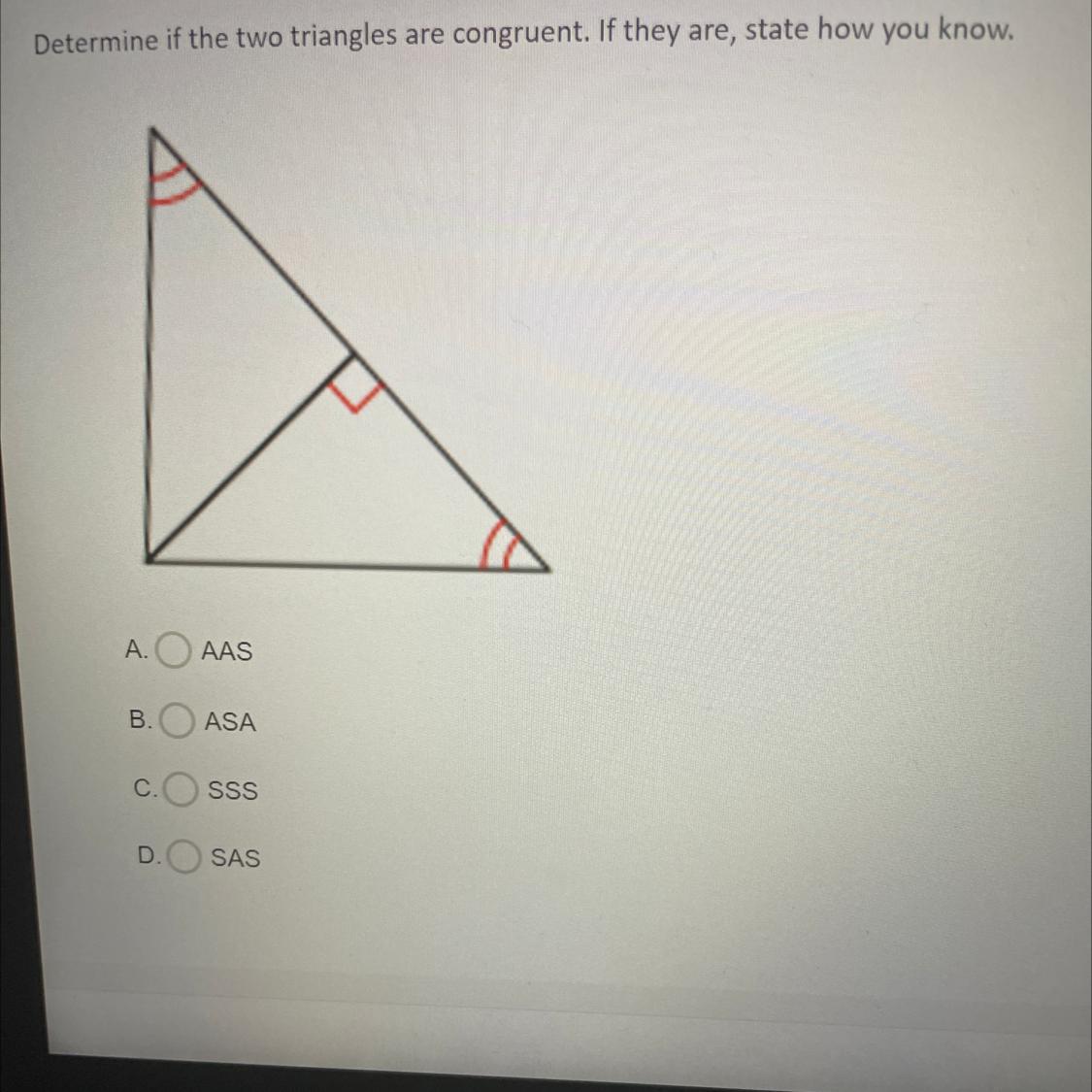
Answers
Answer:
not congruent
Step-by-step explanation
only one side has a 90 degree angle
Simplify the expression (ab^2)*(-b^4a^3)^2
Answers
if any doubt leave a comment below

HEELLLLLLLLLLLLLLLLPPPPPPPPPPP PLZZZZZZZZZ!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!1

Answers
Answer:
x = 21
Step-by-step explanation:
equation:
⇒ 44 + 6x + 10 = 180
add like terms:
⇒ 44 + 6x + 10 = 180
⇒ 54 + 6x = 180
subtract 54 on both sides
⇒ 54 - 54 + 6x = 180 - 54
⇒ 6x = 126
divide 6 on both sides
⇒ \(\frac{6x}{6} = \frac{126}{6}\)
⇒ x = 21
to check:
44 + (6x + 10) = 180
44 + (6 x 21 + 10) = 180
44 + 136 = 180
180 = 180
6x+10 and 44 are supplementary angles, therefore they will equal 180.
now we have the equation 6x+10+44=180
now we solve for x and get 21
I need help ASAP thank you

Answers
Answer:
Volume: 1080
Surface area: 654
Step-by-step explanation:
Part A:
How to solve surface Area: 2×(9×15 + 9×8 + 15×8)
How to solve volume: 9x15x8
Part B:
Surface Area
Part C:
Volume
Hope this helps
Given AC and BD bisect each other at O prove AC is congruent to c

Answers
The Value of CD from the second equation into the first equation:2AC = AB + OC + OD⇒ 2AC = AB + AB (By substituting OC = OA and OD = OB)⇒ 2AC = 2AB⇒ AC Therefore, AC is Congruent to c .
Since AC and BD bisect each other at O, we can say that AO = OC and BO = OD.
We need to prove that AC = CD.To do this, we can use the segment addition postulate which states that if a line segment is divided into two parts, the length of the whole segment is equal to the sum of the lengths of the two parts.
Let us draw a diagram to represent the given information:From the diagram, we can see that:AO + OB = AB (By segment addition postulate)OC + OD = CD (By segment addition postulate)AO = OC (Given)BO = OD (Given)
Now, we can substitute the values of AO and OC as well as BO and OD into the equations above:AO + OB = AB ⇒ OC + OB = AB (Substituting AO = OC)OC + OD = CDNow, we can add both equations:OC + OB + OC + OD = AB + CD ⇒ 2(OC + OD) = AB + CDWe know that OC = AO and OD = BO.
Therefore, we can write:2(AO + BO) = AB + CDSince AO = OC and BO = OD, we can write:2(OA + OD) = AB + CDNow, substituting AO = OC and BO = OD, we can write:2AC = AB + CD
Finally, we can substitute the value of CD from the second equation into the first equation:2AC = AB + OC + OD⇒ 2AC = AB + AB (By substituting OC = OA and OD = OB)⇒ 2AC = 2AB⇒ AC
Therefore, AC is congruent to c .
For more questions on Congruent.
https://brainly.com/question/1675117
#SPJ8
Translate this sentence into an equation. The product of Mabel's age and 4 is 56. Use the variable m to represent Mabel's age.
Answers
Answer:
4m = 56
Step-by-step explanation:
4 * m = 56
4m = 56
4/4m = 56/4
m = 14
I don't need help but I am giving the answer to everyone :) hope it helps

Answers
The number of cannonballs in illustration is 506.
What is illustration?Math Illustrations enables you to produce more useful geometry figures for your students in less time by fusing the constraint-based design of Geometry Expressions with simple-to-use sketching and graphing features.
The number of cannonballs in the first layer = 1² = 1
Number of cannonballs in the second layer = 2² = 4
Number of cannonballs in the third layer = 3² = 9
So, the generalized formula to count the balls is given as
= n(n + 1) (2n + 1)/ 6
Here, n= the total number of layers
Put n =11
11(11 + 1)(2(11) + 1) / 6
= 11(12)(23)/6
= 3036/6
= 506
To learn more about illustration, visit:
https://brainly.com/question/17221744
#SPJ1
Help I need the intercept please.

Answers
At a business meeting at Panera Bread , the bill for two cappuccinos and three caffe lattes was $19.75. At another table, the bill for one cappuccino and two lattes was $11.97 . How much did each type of beverage cost? Help!!
Answers
Answer:
too much
Step-by-step explanation:
i'm broke
A student is graduating from college in 18 months but will need a loan in the amount of $6,720 for the last three semesters. The student may receive either an unsubsidized Stafford Loan or
a PLUS Loan. The terms of each loan are:
Unsubsidized Stafford Loan: annual interest rate of 3.99%, compounded monthly, and a grace period of six months from time of graduation.
PLUS loan: annual interest rate of 4.99%, compounded monthly, with a balance of $7,241.17 at graduation
Which loan will have a higher balance and by how much at the time of repayment?
O The Stafford loan will have a higher balance by $107.41 at the time of repayment.
O The PLUS loan will have a higher balance by $107.41 at the time of repayment.
O The Stafford loan will have a higher balance by $36.53 at the time of repayment.
O The PLUS loan will have a higher balance by $36.53 at the time of repayment.
Answers
The Stafford loan will have a higher balance of $36.53 at the time of repayment.
The correct option is C.
What is a loan calculation formula?The formula:
PV = PMT/i[1 - {1/(1+i)ⁿ]
PV denotes the loan sum.
PMT stands for "monthly payment," I for "interest rate" (interest rate % divided by 12), and "n" for the number of months (term of the loan in months)
To compare the balances of the two loans at the time of repayment, we need to calculate the total amount owed for each loan.
For the Unsubsidized Stafford Loan:
The total loan amount is $6,720, and the annual interest rate is 3.99%, compounded monthly.
Therefore, the monthly interest rate is 3.99% / 12 = 0.3325%. The loan has a grace period of 6 months, so interest will not start accruing until 6 months after graduation.
The loan will be repaid over a period of 10 years, or 120 months.
Using the formula for the future value of an annuity, the total amount owed for the Unsubsidized Stafford Loan is:
FV = PMT x [(1 + r)ⁿ - 1] / r
where PMT is the monthly payment, r is the monthly interest rate, and n is the number of months.
We can solve PMT using a loan repayment calculator, such as the one found on bankrate.com, and we get a monthly payment of $73.80. Plugging this into the formula, we get:
FV = $73.80 x [(1 + 0.003325)¹¹⁴ - 1] / 0.003325
FV = $9,222.41
Therefore, the total amount owed for the Unsubsidized Stafford Loan at the time of repayment is $9,222.41.
For the PLUS Loan:
The loan amount is $7,241.17, and the annual interest rate is 4.99%, compounded monthly. Therefore, the monthly interest rate is 4.99% / 12 = 0.4158%. Interest starts accruing immediately, and the loan will be repaid over a period of 10 years, or 120 months.
Using the same formula, the total amount owed for the PLUS Loan is:
FV = PMT x [(1 + r)ⁿ- 1] / r
Again, using a loan repayment calculator, we get a monthly payment of $78.93. Plugging this into the formula, we get:
FV = $78.93 x [(1 + 0.004158)^120 - 1] / 0.004158
FV = $9,258.94
Therefore, the total amount owed for the PLUS Loan at the time of repayment is $9,258.94.
Comparing the two loan amounts, we see that the Unsubsidized Stafford Loan will have a higher balance of $36.53 ($9,222.41 - $9,258.94) at the time of repayment.
Therefore, the answer is:
The Stafford loan will have a higher balance of $36.53 at the time of repayment.
To learn more about loan calculations;
https://brainly.com/question/28244942
#SPJ1
g^4+ 5h
when g=2 & h=4
Answers
Answer: 36
Step-by-step explanation:
g^4+5h
2^4+5(4)
16+20
36
Help please!! I’ll give brainliest if you show work as well. Thank you!!!

Answers
Answer:
TWO CRACKERS
Step-by-step explanation:
I'm assuming they want to find x. Here we see that these two are similar triangles, so the sides are reflective. 5x/5 should be equal to 4/x, so 5x/5 = 4/x. If we use cross multiplying we get 5x^2 = 20. divide both sides by 5 and we get x^2 = 4 or x = 2.
Hope this helped
During the exponential phase, e.coli bacteria in a culture increase in number at a rate proportional to the current population. If growth rate is 1.9% per minute and the current population is 172.0 million, what will the population be 7.2 minutes from now?
Answers
During the exponential phase, e.coli bacteria in a culture increase in number at a rate proportional to the current population. If growth rate is 1.9% per minute and the current population is 172.0 million, the population 7.2 minutes from now can be calculated using the following formula:
P(t) = P ₀e^(rt)where ,P₀ = initial population r = growth rate (as a decimal) andt = time (in minutes)Substituting the given values, P₀ = 172.0 million r = 1.9% per minute = 0.019 per minute (as a decimal)t = 7.2 minutes
The population after 7.2 minutes will be:P(7.2) = 172.0 million * e^(0.019*7.2)≈ 234.0 million (rounded to the nearest tenth)Therefore, the population of e.coli bacteria 7.2 minutes from now will be approximately 234.0 million.
For more such questions on population
https://brainly.com/question/29885712
#SPJ8
Fred needs to write the equation of the line. He used (10, 64) and (12.5, 73) to find the slope, which is 3.6. The equation of the trend line is
Answers
Answer:
y = 3.6x + 28
Step-by-step explanation:
y = Mx + c
64 = 3.6(10) + c
64 = 36 + c
64 - 36 = c
28 = c
Find the slope of the line to the right.

Answers
9514 1404 393
Answer:
-3/2
Step-by-step explanation:
Points are marked 2 units apart on the x-axis. Between a given point and the one to its right, the y-value changes by -3. The slope is ...
slope = rise/run = (change in y)/(change in x)
slope = -3/2
Find the missing number so that the equation has no solutions.
5x + 18 = -x − 7 + x
Answers
The missing number in the equation is 4
How to determine the missing numberFrom the question, we have the following parameters that can be used in our computation:
5x + 18 = -x − 7 + x
Express the blanks properly
So, we have
5x + 18 = []x − 7 + x
For the equation to have no solution, the following must be true
5x = []x + x
So, we have
[]x = 4x
Divide
[] = 4
Hence, the missing number is 4
Read more about equation at
https://brainly.com/question/2972832
#SPJ1
In the Gaussian integral, how does the left side of this equation equal the right side? An answer would be really appreciated, thank you.

Answers
the left side of this equation equal the right side through the process of completing the square that establishes the equality between the left side and the right side of the Gaussian integral equation.
How do we calculate?
using completing the square method:
Starting with the left side of the equation:
∫\(e^(^-^x^2)\) dx
\(e^(^-^x^2) = (e^(^-x^2/2))^2\)
∫\((e^(^-^x^2/2))^2 dx\)
let u = √(x²/2) = x = √(2u²).
dx = √2u du.
∫ \((e^(^x^2/2))^2 dx\)
= ∫ \((e^(^-2u^2)\)) (√2u du)
The integral of \(e^(-2u^2)\)= √(π/2).
∫ \((e^(-x^2/2))^2\) dx
= ∫ (√2u du) \((e^(-2u^2))\\\)
= √(π/2) ∫ (√2u du)
We substitute back u = √(x²/2), we obtain:
∫ \((e^(-x^2/2))^2\)dx
= √(π/2) (√(x²/2))²
= √(π/2) (x²/2)
= (√π/2) x²
A comparison with the right side of the equation shows that they are are equal.
Learn more about Gaussian integral equation at:
https://brainly.com/question/33550421
#SPJ1
Solve for brainliest

Answers
Answer:
Step-by-step explanation:
In this equation, 500 is the coefficient of the variable h, 4,000 is the constant, and E and h are both variables. Therefore, the equation should be written as:
E = 500h + 4000
Question 2 help please

Answers
Answer:
The measure of the vertex angle is 94 degrees ⇒ A
Step-by-step explanation:
In any triangle, the sum of the measures of its interior angle is 180°In the isosceles triangle, the two base angles are equal in measures∵ In an isosceles triangle, the measure of the base angle = (2x + 5)
∵ The base angles of the isosceles triangles are equal in measures
∴ The measures of the base angles are (2x + 5), (2x + 5)
∵ The measure of the vertex angle = (5x - 1)
∵ The sum of the measure of the three angles = 180°
∴ (2x + 5) + (2x + 5) + (5x - 1) = 180
→ Add the like terms in the left side
∵ (2x + 2x + 5x) + (5 + 5 + -1) = 180
∴ 9x + 9 = 180
→ Subtract 9 from both sides
∴ 9x + 9 - 9 = 180 - 9
∴ 9x = 171
→ Divide both sides by 9 to find x
∴ x = 19
→ Substitute the value of x in the measure of the vertex angle to find it
∵ The measure of the vertex angle = 5x - 1
∴ The measure of the vertex angle = 5(19) - 1
∴ The measure of the vertex angle = 95 - 1
∴ The measure of the vertex angle = 94°
∴ The measure of the vertex angle is 94 degrees
Hexagon DEFGHI is translated on the coordinate plane below to create hexagon D′E′F′G′H′I′: Hexagon DEFGHI and Hexagon D prime E prime F prime G prime H prime I prime on the coordinate plane with ordered pairs at D 2, 5, at E 5, 5, at F 6, 3, at G 5, 1, at H 2, 1, at I 1, 3, at D prime negative 6, negative 2, at E prime negative 3, negative 2, at F prime negative 2, negative 4, at G prime negative 3, negative 6, at H prime negative 6, negative 6, at I prime negative 7, negative 4
Answers
Answer: To find the image of a figure under a translation, you need to apply the same translation to every point in the figure.
In this case, the image of hexagon DEFGHI is hexagon D′E′F′G′H′I′. To find the image of each point, you can apply the translation that maps point D to point D′.
For example, to find the image of point E under the translation, you can apply the same translation that maps point D to point D′:
Point D is located at (2, 5).
Point D′ is located at (-6, -2).
The translation that maps point D to point D′ is a translation 6 units to the left and 2 units down.
To find the image of point E under this translation, you can apply the same translation to point E:
Point E is located at (5, 5).
The image of point E is located at (5 - 6, 5 - 2) = (-1, 3).
You can follow the same process to find the images of the other points under the translation.
Alternatively, you can use the coordinates of point D and point D′ to find the translation vector that describes the translation. The translation vector is a displacement that describes the change in position of a point under the translation.
In this case, the translation vector is given by the displacement from point D to point D′:
Point D is located at (2, 5).
Point D′ is located at (-6, -2).
The translation vector is given by the displacement (-6 - 2, -2 - 5) = (-8, -7).
To find the image of any point under the translation, you can add the translation vector to the coordinates of the point. For example, to find the image of point E under the translation, you can add the translation vector to the coordinates of point E:
Point E is located at (5, 5).
The translation vector is (-8, -7).
The image of point E is located at (5 - 8, 5 - 7) = (-3, -2).
You can follow the same process to find the images of the other points under the translation.
Step-by-step explanation:
Is this the correct answer?

Answers
Answer:
Yes. This is half a square, a full square has 360 degrees total because it has 4 right angles which are each 90. We know that there is a 50 degree and 90 degree angle, and since this is split it is 180 total. 180-140=40 degrees, so yes.
Bob rides his bike he records his time and distance each time he stops for water how many miles will Bob have traveled if you stopped after 180 minutes continue in the same pattern enter your answer in the first response parks and to the equation represents the relationship between Bob’s distance and the time he stops for water in the second response box use D for the distance you travel in t for the time in minutes
Answers
The equation represents of Bob’s distance is D = 1/4t
How to determine the equation represents of Bob’s distanceThe complete question is added as an attachment
From the question, we have the following parameters that can be used in our computation:
The table of values
On the table of values, we can see that
The distance multiplied by 4 gives the time
Mathematically, this is represented as
4 * D = t
Divide by 4
D = 1/4t
Hence, the equation is D = 1/4t
Read more about functions at
https://brainly.com/question/4025726
#SPJ1

please help now i hate this i keep getting a 60!!!


Answers
Answer: b
Step-by-step explanation:
it goes up by 8 each time
Please use the Quadratic Formula to find the zeros of the function below.
g(x) = 2x2 + x + 25
Answers
Answer:
Step-by-step explanation:

HELP PLEASE I NEED HALP

Answers
Answer:
16
Step-by-step explanation:
8x2
Which of the following equations has the solution x= all real numbers?

Answers
After solving the equations, the equation which holds true for every real number x will be equal to 5(3 - x) + 7x = 3x + 15 - x. Hence, option B is correct.
What is an equation?Mathematical expressions with two algebraic symbols on either side of the equal (=) sign are called equations.
This relationship is illustrated by the left and right expressions being equal to one another. The left-hand side equals the right-hand side is a basic, straightforward equation.
As per the given information in the question,
Let's check the option one by one,
A.
5(3 - x) + 7x = 3x + 10 - x
15 - 5x + 7x = 2x + 10
2x + 15 = 2x + 10
2x - 2x = 10 - 15
0 = -5, this is not possible.
B.
5(3 - x) + 7x = 3x + 15 - x
15 - 5x + 7x = 2x + 15
2x + 15 = 2x + 15
Here, we can see that LHS = RHS are equal, then this holds true for every real number x.
2x - 2x = 15 - 15
0 = 0, universally true.
To know more about equation:
https://brainly.com/question/29657983
#SPJ1
The domain of (fg)(x) consists of the numbers x that are in the domains of both f and g.
Answers
The statement "The domain of (fg)(x) consists of the numbers x that are in the domains of both f and g" is FALSE.
Domain is the values of x in the function represented by y=f(x), for which y exists.
THe given statement is "The domain of (fg)(x) consists of the numbers x that are in the domains of both f and g".
Now we assume the \(g(x)=x+2\) and \(f(x)=\frac{1}{x-6}\)
So here since g(x) is a polynomial function so it exists for all real x.
\(f(x)=\frac{1}{x-6}\) does not exists when \(x=6\), so the domain of f(x) is given by all real x except 6.
Now,
\((fg)(x)=f(g(x))=f(x+2)=\frac{1}{(x+2)-6}=\frac{1}{x-4}\)
So now (fg)(x) does not exists when x=4, the domain of (fg)(x) consists of all real value of x except 4.
But domain of both f(x) and g(x) consists of the value x=4.
Hence the statement is not TRUE universarily.
Thus the given statement about the composition of function is FALSE.
Learn more about Domain here -
https://brainly.com/question/2264373
#SPJ10
consider a two-factor factorial design with three levels for facts a, three levels for factor b, and four replicates in each of the nine cells
a. how many degrees of freedom are there in determining the A variation and the factor B variation
b. how many degrees of freedom are there in dreaming the interaction variation
c. how many degrees of freedom are there in determining the random variation
d. how many degrees of freedom are there in determining the total variation
Answers
In calculating the factor A variation, there are two degrees of freedom. In determining the variation of factor B, there are two degrees of freedom.
What is a two-factorial design?A two-factor factorial design is an experiment that collects data for all potential values of the two factors of the study. The design is a balanced two-factor factorial design if equivalent sample sizes are used for every of the possible factor combinations.
Suppose we have two components, A and B, each of which has a high number of levels of interest. We will select a random level of component A and a random level of factor B, and n observations will be taken for each experimental combination.
From the data given:
a.
In calculating the factor A variation, there are two degrees of freedom.
In determining the variation of factor B, there are two degrees of freedom.
b.
Finding the degree of freedom using the interaction variation, there are four degrees of freedom.
c.
In finding the random variable, there are 9(4-1) = 27 degrees of freedom.
d.
In calculating the total variable, there are 9*4-1 =35 degrees of freedom.
Learn more about using a two-factor factorial design for determining the degree of freedom here:
https://brainly.com/question/14292694
#SPJ1