Answers
Answer:
See below
Step-by-step explanation:
The domain of \(f\) is non-negative real numbers, and the domain of \(g\) is real numbers.
\((f\circ g)(x) = 2\sqrt{2}|x|^5\) (I skipped calculation details), so \((f\circ g)(9) = 2 \sqrt{2} \cdot 9^5\).
Related Questions
Brainliest to the one thats right
Answers
Answer:
Option C is correct.
Step-by-step explanation:
In option C, the fractions are on one side and the constants are on the other. The fractions also have the same denominator. So, Option C is correct.
Consider the polynomial
(4mn^2n - 2mn + 6) + (6mn^2 - 1) - (mn^2 - 2 + 9mn)
Combine all like terms and enter the coefficients for each term into the blanks below
Answers
The required coefficients are:4, -1, -11, and 7.
Coefficients refer to the numerical values that are assigned to variables in mathematical equations, models, or formulas. They indicate the relative importance or contribution of each variable in the equation. Coefficients are used to determine the relationship between variables and are often estimated through statistical analysis or optimization techniques.
In algebraic equations, coefficients are the numbers multiplied by variables. For example, in the equation 2x + 3y = 5, the coefficients are 2 and 3.
In statistical models, such as linear regression, coefficients represent the slopes or weights assigned to the predictor variables. These coefficients indicate how much the response variable is expected to change for a unit change in the corresponding predictor variable, assuming all other variables are held constant.
We need to consider the polynomial:
(4mn^2n - 2mn + 6) + (6mn^2 - 1) - (mn^2 - 2 + 9mn)
To combine the like terms and find the coefficients of each term, we can write the polynomial in the following form:
4mn^2n - 2mn + 6 + 6mn^2 - 1 - mn^2 + 2 - 9mn
Taking the coefficients of the terms with "mn^2"4mn^2n - mn^2
Taking the coefficients of the terms with "mn"-2mn - 9mn = -11mn
Taking the coefficients of the constant terms6 + 2 - 1 = 7
Therefore, the required coefficients are:4, -1, -11, and 7.
For more such questions on coefficients , Visit:
https://brainly.com/question/1038771
#SPJ8
Determine the correct inventory amount on December 31.
I am so lost and have no clue what to do. Any help is appreciated!
Answers
The adjusted balance of Blossom's inventory account is $214,680.
Define rate of interestThe rate of interest, also known as the interest rate, is the percentage amount charged by a lender or financial institution for the use of borrowed money or for the extension of credit. It is the cost of borrowing money, typically expressed as an annual percentage of the amount borrowed or owed.
Goods shipped FOB shipping point on December 28 to Splish Company for $53,940 were not included in the physical inventory count. Therefore, we need to add this amount to the year-end balance of inventory:$286,950 + $53,940 = $340,890Goods shipped FOB destination to Blossom for $97,100 were not included in the physical inventory count. Therefore, we need to subtract this amount from the year-end balance of inventory: $340,890 - $97,100 = $243,79Goods received FOB shipping point on January 2 for $26,120 were not included in the physical inventory count. Therefore, we need to add this amount to the year-end balance of inventory: $243,790 + $26,120 = $269,91Goods shipped FOB destination to Ehler of Canada for $55,230 were not included in the physical inventory count. Therefore, we need to subtract this amount from the year-end balance of inventory: $269,910 - $55,230 = $214,680Goods received FOB destination on January 2 for $38,960 were included in the physical inventory count. Therefore, we do not need to make any adjustments for this transaction.Therefore, the adjusted balance of Blossom's inventory account is $214,680.
To know more about percentage , visit:
https://brainly.com/question/29306119
#SPJ1
Which answers describe the shape below? Check all that apply.
31
A
A. Quadrilateral
B. Rhombus
C. Trapezoid
D. Parallelogram
E. Rectangle
F. Square
Answers
Answer:
A and D are correct. This is a parallelogram, which is a quadrilateral. B is not correct because not all the sides are congruent. C is not correct. E and F are not correct because this parallelogram does not have any right angles.
how do u solve this problem 1 1/4 x 42/3
Answers
Answer:
17.5
Step-by-step explanation:
{ 1 \(\frac{1}{4}\) = 5/4 }
1 \(\frac{1}{4}\) * 42/3 = 5/4 * 42/3
= 210/12
= 17.5
A jar contains 7 red marbles and 10 blue marbles. What is the probability of choosing a blue marble?
This answer should be written as a decimal. Answer to two decimal places.
Answers
The probability of choosing a blue marble is 0.59.
What is probability?Probability is the occurence of likely events. It is the area of mathematics that deals with numerical estimates of the likelihood that an event will occur or that a statement is true. An event's probability is a number between 0 and 1.
The jar contains 7 red marbles and 10 blue marbles.
The probability of choosing a blue marble will be:
= Number of blue marbles / Total marbles
= 10/17
= 0.59
Learn more about probability on:
brainly.com/question/24756209
#SPJ1
Help what type of function is this
Answers
A right rectangular prison is shown with some measurements given in units. The length of the diagonal from point A to point B is 13 units. What is the height, h, of the prison in units?
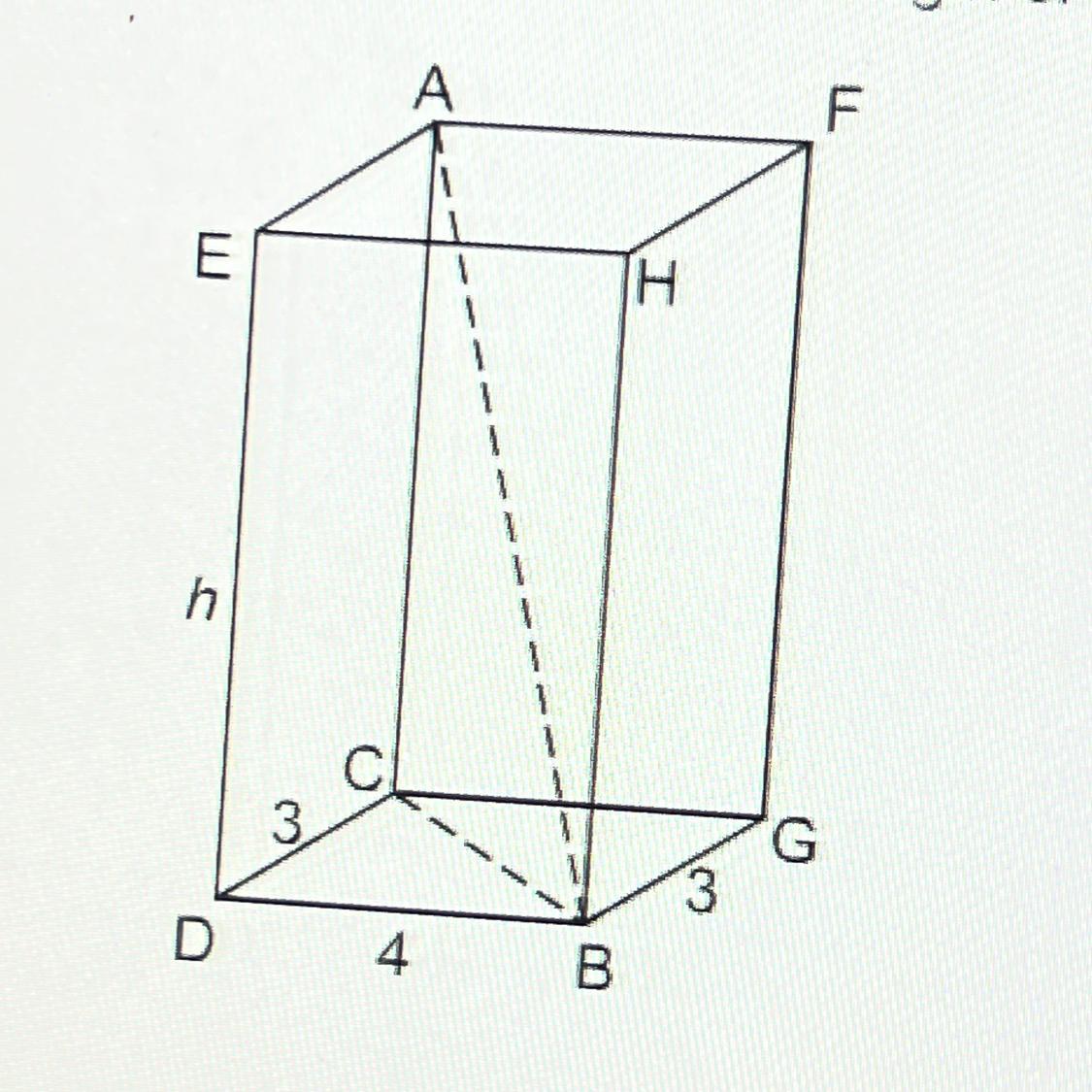
Answers
The required value of h, representing the height of the three-dimensional rectangle, is 12.
The diagonal of a three-dimensional rectangle is defined by the equation d² = x² + y² + h². To solve for h, we can rearrange the equation as follows:
h² = d² - x² - y²
Given the values d = 13, x = 3, and y = 4, we can substitute them into the equation:
h² = 13² - 3² - 4²
h² = 169 - 9 - 16
h² = 144
Taking the square root of both sides, we find:
h = 12
Therefore, the value of h, representing the height of the three-dimensional rectangle, is 12.
Learn more about the diagonal of the right rectangular prison here:
https://brainly.com/question/13839054
#SPJ1
prove that n!<n^n for n≥2
Answers
Answer:
Step-by-step explanation:
Hello,
We will prove it by induction.
Step 1 - for n=2
2!=2*1=2
2^2=4
and 2 < 4 so this is true for n=2
Step2 - We assume that this is true for k and we have to prove it for k+1.
Induction hypothesis is \(k!<k^k\)
\((k+1)!=(k+1)k!\)
We use the induction hypothesis and we we can write that
\((k+1)!=(k+1)k!<(k+1)k^k<=(k+1)(k+1)^k=(k+1)^{k+1}\\\\\text{As }k <= k+1\)
so, we prove it for k+1
Step 3- conclusion
for n >= 2 we just proved that \(n!<n^n\)
Circle Project 1. Draw a point at (1, -2) 2. Draw an 8-unit long radius 3. Using a compass, Draw a circle with your point from step one as your center and the point from step two as the side. 4. Using a protractor, draw a 70 degree arc 5. Draw a central angle which intercepts your arc 6. Draw an inscribed angle which intercepts a 40 degree arc 7. Draw a tangent line 8. Draw a secant line 9. Write the equation of your circle.
Answers
Answer:
I can explain how to complete each of the steps you have provided.
1. Draw a point at (1, -2)
This is a simple step. Just mark a dot on your paper at the coordinates (1, -2).
2.
Draw an 8-unit long radius
Using your compass, set the radius to 8 units. Place the compass on the point you drew in step 1 and draw a circle around it, making sure that the radius is 8 units long.
3. Using a compass
Draw a circle with your point from step one as your center and the point from step two as the side: This step is already completed in step 2.
4. Using a protractor draw a 70 degree arc
Place your protractor on the center of the circle (the point you drew in step 1) and draw a 70 degree arc on the circle.
5. Draw a central angle which intercepts your arc
Use a straight edge to draw a line from the center of the circle to each endpoint of the arc you drew in step 4. This creates a central angle, which is an angle whose vertex is at the center of the circle and whose sides intercept the circle.
6. Draw an inscribed angle which intercepts a 40 degree arc
Use a straight edge to draw a line from one endpoint of the 70 degree arc to the other endpoint. Then, draw a perpendicular bisector of this line, which intersects the center of the circle. This creates a 40 degree arc on the circle. Draw a line from the center of the circle to one endpoint of the 40 degree arc, and draw a line from that endpoint to the other endpoint of the 40 degree arc. This creates an inscribed angle, which is an angle whose vertex is on the circle and whose sides intercept the circle.
7. Draw a tangent line
Choose a point on the circle that is not on the 70 degree arc. Draw a line from that point tangent to the circle.
8. Draw a secant line
Choose two points on the circle that are not on the 70 degree arc. Draw a line through those points, which intersects the circle at two points.
9. Equation of your circle
The equation of a circle with center (a,b) and radius r is (x-a)^2 + (y-b)^2 = r^2. Using the coordinates of the center from step 1 and the radius from step 2, the equation of the circle is (x-1)^2 + (y+2)^2 = 64.
what is an equation of the line that is parallel to y=-5+6 and passes through the poing (-4,-1)
Answers
Answer:
y=5x+19
Step-by-step explanation:
y+1=-5(x+4)
y+1=-5x-20
Subtract 1 (like terms)
y=-5x-21
Larry starts at the bottom of a long staircase. He climbs exactly of the stairs. Then, he goes back down exactly 2/3 of the way to the bottom. From that spot, he climbs exactly of the way to the top. Finally, from there he 1/2 2/3 climbs 6 stairs to reach the top. How many stairs are in the staircase?
Answers
There are a total of 27 steps on the staircase.
What are Fractions?Fractions are numbers which are of the form a/b where a and b are real numbers. This implies that a parts of a number b.
Let x be the total number of steps in the staircase.
Larry climbs exactly 2/3 of the stairs.
Number of steps Larry climbed = 2x/3
She goes back exactly 1/2 of the way to the bottom.
Number of steps returned = (2x/3) (1/2) = 2x/6 = x/3
She is at x/3 steps from the bottom.
From that spot, she climbs exactly 2/3 of the way to the top.
Remaining steps to the top = x - x/3 = 2x/3
Number of steps Larry climbed = 2/3 of the way to the top = (2/3)(2x/3) = 4x/9
So we get,
x/3 + 4x/9 + 6 = x
x - x/3 - 4x/9 = 6
x - 7x/9 = 6
2x/9 = 6
2x = 54
x = 27
Hence there are 27 steps in the staircase.
To learn more about Fractions, click :
https://brainly.com/question/8482939
#SPJ1
The complete question is as follows :
Lara starts at the bottom of a long staircase. She climbs exactly 2/3 of the stairs. Then, she goes back down exactly 1/2 of the way to the bottom. From that spot, she climbs exactly 2/3 of the way to the top. Finally from there, she climbs 6 stairs to reach the top. How many stairs are in the staircase?
A cylinder has a base radius of 9 feet and a height of 4 feet. What is its volume in
cubic feet, to the nearest tenths place?
Answers
The volume of the cylinder will be equal to 1017.87 cubic feet.
What is volume?Volume is defined as the space occupied by any object in the three-Dimensions. For the cylinder, the volume will be calculated by radius and the height of the cylinder.
Given that:-
The volume of the cylinder will be calculated by using the formulas below:-
V = πr²h
V = π ( 9 )² 4
V = 1017.87 cubic feet.
Therefore the volume of the cylinder will be equal to 1017.87 cubic feet.
To know more about Volume follow
https://brainly.com/question/1972490
#SPJ1
27. What is the reflection image of (5, –3) across the y-axis? (–5, 3) (–5, –3) (–3, 5) (5, 3)
Answers
The search results are unrelated to the question of finding the reflection image of (5, -3) across the y-axis. To find the reflection image of a point across the y-axis, we need to change the sign of the x-coordinate of the point. Therefore, the reflection image of (5, -3) across the y-axis is (-5, -3).
Use the graph of the parabola to fill in table
Answers
Solution
a) The parabola opens downward
b) x - intercept is: -6 , -2
y-intercept is: -3
c) Vertex is the turning point: (-4, 1)
d) The axis of symmetry is x = -4
The box plots below show the math scores of students of two different classes, which statement is correct
Answers
Answer:
B
Step-by-step explanation:
Given the data:
Class A 55 72 75 89 95
Class B 55 70 75 94 100
CLASS A :
Minimum - 55
Lower quartile - 72
Median - 75
Upper quartile - 89
Maximum - 95
CLASS B :
Minimum - 55
Lower quartile - 70
Median - 75
Upper quartile - 94
Maximum - 100
Evaluating the statements given :
The median score of Class A is greater than the median score of Class B.
Median A = 75 ; Median B = 75 (median are equal), hence, A is not true
The lower quartile of Class A is greater than the lower quartile of Class B.
Lower quartile A = 72 ; Lower quartile B = 70 (A is greater than B) , hence, B is true
The upper quartile of Class A is greater than the upper quartile of Class B.
Upper quartile A = 89 ; Upper quartile B = 94 (A is less than B) , hence, statement is not true
The maximum score of Class A is greater than the maximum score of Class B.
Maximum A = 94 ; maximum B = 100 ; A < B ; Hence, statement is not true
Factor the expression using the GCF 2r - 10
Answers
Answer:2(r-5)
Step-by-step explanation: divide 2 on both sides which gives you 5 and then you write 2(r-5).
Hope it helps :)
The perimeter of a rectangular room is 60 feet. Let x be the width of the room (in feet) and let y be the length of the room (in feet). Select all of the equations below that could model this
situation
A. 2(x + y) = 60
B. 2x + 2y = 60
C. x+2y = 60
D. 2x + y = 60
E. x+y = 60
Answers
Answer:
A and B are the correct answers
The equation that represent the given situation is 2 ( x +y) = 60 and 2x +2y = 60, the correct option is A, and B.
What is an Equation?An equation is a mathematical statement formed when two algebraic expressions are equated using an equal sign.
The equations are useful in determination of unknown parameters.
A rectangle is a polygon with four sides, the opposite sides of a rectangle is parallel and equal.
The perimeter of a rectangular room is 60 feet.
The perimeter of a rectangle is given by,
P = 2 ( Length + Breadth)
Let x be the width of the room (in feet).
Let y be the length of the room (in feet).
Substituting the values in the formula to get the equation.
60 = 2 ( x +y)
2 ( x +y) = 60 ---------- (1)
2x +2y = 60 ------------(2)
Therefore, the equations that could model this is situation 2 ( x +y) = 60 and 2x +2y = 60.
To know more about Equation
https://brainly.com/question/10413253
#SPJ6
Suppose that 40% of all adults regularly consume coffee, 50% regularly consume carbonated soda, and 60% regularly consume at least one of these two products
Answers
logan is buying his baby sister a stacking toy with his allowance. the cost of a wooden stacking toy is $25.50. a plastic stacking toy costs 1/3 the price of the wooden toy. sales tax on either would be 6%. how much more will logan pay if he buys the wooden toy instead of the plastic toy?
Answers
Logan will pay $18.02 more if he buys the wooden stacking toy instead of the plastic stacking toy.
The cost of the plastic stacking toy is 1/3 the cost of the wooden stacking toy:
Cost of plastic toy = (1/3) x $25.50 = $8.50
If Logan buys the wooden toy, he will pay:
Cost of wooden toy = $25.50
To find the amount of sales tax on either toy, we can multiply the cost of the toy by the tax rate of 6%:
Sales tax = 6% x cost of toy
Sales tax on the wooden toy = 6% x $25.50 = $1.53
Sales tax on the plastic toy = 6% x $8.50 = $0.51
If Logan buys the wooden toy, he will pay an extra:
Total cost difference = Cost of wooden toy - Cost of plastic toy + Sales tax on wooden toy - Sales tax on plastic toy
Total cost difference = ($25.50 - $8.50) + ($1.53 - $0.51)
Total cost difference = $17 + $1.02
Total cost difference = $18.02
To learn more about toy here:
brainly.com/question/13338775
#SPJ1
Solve for x
2/5(2)^x = 32/5
Answers
Rearrange = 2^ 1+x /5 =32/5
Multiply = 5 x 2^x+1/5 = 5 x 32/5
Cancel multiplied terms in denominator= 2^ x+1=32
X +1=5
Subtract 1 from both sides
X+1-1= 5-1
New term= x=5-1=4
X=4
Show how to answer thanks
A rectangle has a length that is 1 more than three times the width the area is 52 square feet. find the length and the width
Answers
9514 1404 393
Answer:
width: 4 ftlength: 13 ftStep-by-step explanation:
Let w represent the width of the rectangle. Then the length is 3w+1 and the area is ...
w(3w+1) = 52
3w² +w -52 = 0
To factor this equation, we need factors of 3·52 = 156 that have a difference of 1. These values are 12 and 13, so we can rewrite the equation as ...
3w² +13w -12w -52 = 0
w(3w +13) -4(3w +13) = 0
(w -4)(3w +13) = 0
The positive value of w that makes a factor zero is ...
w = 4
Then the length is 3w+1 = 3(4) +1 = 13.
The length is 13 ft; the width is 4 ft.
Please Help!! Solve For X
Answers
The value of x in the given figure is 8.
In the given figure there are two lines which are parallel.
We have to find the value of x.
In the straight line the sum of angles is 180 degrees.
8x+1+115=180
8x+116=180
Subtract 116 from both sides:
8x=180-116
8x=64
Divide both sides by 8:
x=64/8
x=8
Hence, the value of x in the given figure is 8.
To learn more on Angles click:
https://brainly.com/question/28451077
#SPJ1
prove that a rectangle has congruent diagonals
Answers
Answer:
Look below
Step-by-step explanation:
Lets say there is a rectangle abcd
One way is: Triangle ABC is congruent to triangle DCB
Another way is: Since a rectangle is a parallelogram too, segment ab=dc. This is because opposite sides of a parallelogram are congruent.
what's the way to finding a solution?
Answers
-9x=180
x=-20
Hope it helps! All ya gotta do is add -4 and -5. Which is -9, and then you do 180 divided by -9 and it equals -20
Difference between polynomial and multinational
Answers
Answer: A polynomial is an algebraic expression with 1, 2 or 3 variables, whereas, a multinomial is a type of polynomial with 4 or more variables.
Step-by-step explanation:
which linear equation represents the same relationship shown in the graph Below?
Answers
Notice that the y-intercept of the line in the graph is 5. Set x=0 on the given equations to find which of them satisfy that condition. It turns out that there are two possibilities:
\(y=-\frac{2}{5}x+5\)\(y=-\frac{5}{2}x+5\)Furthermore, we can see that when x=2, then y=0 on the graph. substitute x=2 on those equations to find which of them satisfy that condition:
\(\begin{gathered} y=-\frac{2}{5}(2)+5 \\ =-\frac{4}{5}+5 \\ =4.2 \end{gathered}\)\(\begin{gathered} y=-\frac{5}{2}(2)+5 \\ =-5+5 \\ =0 \end{gathered}\)Then, the equation:
\(y=-\frac{5}{2}x+5\)is the only one which matches the line on the image.
A kitchen sink holds 24 gallons of water. A full sink drains at 3 gal
Answers
What's 48 divided by 2 (9 + 3)
Answers
Answer:
288
Step-by-step explanation:
First add 9 + 3
Then multiply it by 2
Finally divide it with 48
The value of the given expression 48 ÷ 2 (9 + 3) is 288, which is determined by orders of PEMDAS.
To evaluate the expression 48 ÷ 2 (9 + 3), we follow the order of operations, which is commonly known as PEMDAS (Parentheses, Exponents, Multiplication, and Division from left to right, Addition, and Subtraction from left to right).
Let's break down the expression step by step:
Simplify the expression inside the parentheses:
9 + 3 = 12
Multiply:
48 ÷ 2 * 12
Divide:
48 ÷ 2 = 24
Multiply:
24 * 12 = 288
Therefore, the value of the expression 48 ÷ 2 (9 + 3) is 288.
Learn more about the PEMDAS rule here :
https://brainly.com/question/20876480
#SPJ6
What is the value of the below expression?
48÷ 2 (9 + 3)
An isosceles triangle whose sides are 5cm, 5cm and 6cm is inscribed in a circle. Find the radius of the circle.
Answers
Answer:
To find the radius of the circle inscribed in an isosceles triangle, we can use the following formula:
r = (a/2) * cot(π/n)
where r is the radius of the inscribed circle, a is the length of one of the equal sides of the isosceles triangle, and n is the number of sides of the polygon inscribed in the circle.
In this case, we have an isosceles triangle with two sides of 5cm and one side of 6cm. Since the triangle is isosceles, the angle opposite the 6cm side is bisected by the altitude and therefore, the two smaller angles are congruent. Let x be the measure of one of these angles. Using the Law of Cosines, we can solve for x:
6^2 = 5^2 + 5^2 - 2(5)(5)cos(x)
36 = 50 - 50cos(x)
cos(x) = (50 - 36)/50
cos(x) = 0.28
x = cos^-1(0.28) ≈ 73.7°
Since the isosceles triangle has two equal sides of length 5cm, we can divide the triangle into two congruent right triangles by drawing an altitude from the vertex opposite the 6cm side to the midpoint of the 6cm side. The length of this altitude can be found using the Pythagorean theorem:
(5/2)^2 + h^2 = 5^2
25/4 + h^2 = 25
h^2 = 75/4
h = sqrt(75)/2 = (5/2)sqrt(3)
Now we can find the radius of the inscribed circle using the formula:
r = (a/2) * cot(π/n)
where a = 5cm and n = 3 (since the circle is inscribed in a triangle, which is a 3-sided polygon). We can also use the fact that the distance from the center of the circle to the midpoint of each side of the triangle is equal to the radius of the circle. Therefore, the radius of the circle is equal to the altitude of the triangle from the vertex opposite the 6cm side:
r = (5/2) * cot(π/3) = (5/2) * sqrt(3) ≈ 2.89 cm
Therefore, the radius of the circle inscribed in the isosceles triangle with sides 5cm, 5cm, and 6cm is approximately 2.89 cm.