A store sells a package of 25 trading cards 5.25. What is the cost of one trading card
The unit price is _____ per card

Answers
Related Questions
Let f be a nonnegative measurable function on E
(1) Show there is an increasing sequence of nonnegative simple functions on E, each of finite support, which converges pointwise on E to
(2) Show that, f=sup φ simple, of finite supportand 0 os fonE}
Answers
If f is F-measurable and non-negative on E ∈ F and µ(E) = 0
thenREf dµ = 0.ProofLet 0 ≤ s ≤ f be a simple, F-measurable function. So s =PNn=1 anχAnfor some an ≥ 0,
An ∈ F. Then IE(s) = PNn=1 anµ(An ∩ E). But µ ismonotone which means that µ(An ∩ E) ≤ µ(E) = 0 for all n and so IE(s) =0 for all such simple functions.
Hence I(f, E) = {0} and so REf dµ =sup I(f, E) = 0. ¥Lemma 4.7 If g ≥ 0 and REgdµ = 0 thenµ{x ∈ E : g(x) > 0} = 0.Proof Let A = {x ∈ E : g(x) > 0} and An = {x ∈ E : g(x) >1n}.
Thenthe sets An = E ∩ {x : g(x) >1n} ∈ F satisfy A1 ⊆ A2 ⊆ A3 ⊆ ... withA =S∞n=1 An. By lemma 4.1 µ(A) = limn→∞ µ(An). Usingsn(x) = ½ 1nif x ∈ An0 otherwise,so sn ≤ g on An we have1nµ(An) = IAn(sn)≤RAngdµ by the definition of RAn≤REgdµ
Thereom 4.4(iii)= 0 by assumption.So µ(An) = 0 for all n and hence µ(A) = 0. ¥Definition If a property P holds on all points in E \ A for some set A withµ(A) = 0 we say that P holds almost everywhere (µ) on E, written as a.e.(µ)on E.
(*It might be that P holds on some of the points of A or that the set ofpoints on which P does not hold is non-measurable.
This is immaterial. Butif µ is a complete measure, such as the Lebesgue-Steiltje’s measure µF, thenthe situation is simpler.
Assume that a property P holds a.e.(µ) on E.
Thedefinition says that the set of points, D say, on which P does not hold can becovered by a set of measure zero, i.e. there exists A : D ⊆ A and µ(A) = 0.
Yet if µ is complete then D will be measurable of measure zero.In this section we are not assuming that µ is complete.)

pleas anwear fast
Graph the function.
�
(
�
)
=
4
⋅
(
3
2
)
�
f(x)=4⋅(
2
3
)
x
f, left parenthesis, x, right parenthesis, equals, 4, dot, left parenthesis, start fraction, 3, divided by, 2, end fraction, right parenthesis, start superscript, x, end superscript
Answers
The graph of the function f(x) = 4(2/3)^x is added as an attachment
How to determine the graph of the functionFrom the question, we have the following parameters that can be used in our computation:
f(x)=4⋅(
2
3
)
x
Express the equation properly
So, we have
f(x) = 4(2/3)^x
The above expression is a an equation of a exponential function
Next, we plot the graph using a graphing tool
To plot the graph, we enter the equation in a graphing tool and attach the display
See attachment for the graph of the function
Read more about graphs at
https://brainly.com/question/30390162
#SPJ1

What number would come next in this sequence? 1, 2, 6, 22
Answers
The next number in the sequence 1, 2, 6, 22 is 86.
What is Sequence?Sequence is an enumerated collection of objects in which repetitions are allowed and order matters.
The given sequence is 1, 2, 6, 22
Consider the provided sequence 1, 2, 6, 22, ____ ?
Observe the pattern of the sequence.
To obtain the sequence you need to add the next even square of 2 in the previous number.
1+2⁰=2
Now the next even number is 2.
2+2²=6
Now 6+2⁴=6+16=22
Therefore, the next number should be:
22+2⁶=86
Hence, the next number in the sequence 1, 2, 6, 22 is 86.
To learn more on Sequence click:
https://brainly.com/question/21961097
#SPJ1
what is −3x−6+(−1) ?
Answers
Answer:
-3x-7
Step-by-step explanation:
Super is a ride-sharing company. The Chief of Operations wants the revenue (output value) to be seven times the cost of service operations (input cost). Suppose that each regular car earns a value of $1500 per month and premium cars earn $2500 per unit per month. The monthly cost of operating a regular car is $100 per month and $500 per premium car. Super currently has 19 regular cars. How many premium cars do they need to achieve a productivity ratio of 7? (Enter your response rounded to whole number.)
Answers
Super would need 2 premium cars to achieve a productivity ratio of 7.
How to find the productivity ratio?Let's call the number of premium cars "x".
The total revenue from the regular cars would be $1500 * 19 = $28,500 per month.
The total revenue from the premium cars would be $2500 * x.
The total cost of the regular cars would be $100 * 19 = $1900 per month.
The total cost of the premium cars would be $500 * x.
The Chief of Operations wants the revenue to be 7 times the cost of service operations, so we can write the following equation:
($28,500 + $2500x) / ($1900 + $500x) = 7
Expanding and simplifying the equation, we get:
$2500x + $28,500 = 7($1900 + $500x)
$2500x + $28,500 = $13,300 + 7$500x
$11,200 = 6$500x
$11,200 / $6,500 = x
x = 1.723
Rounding up, Super would need 2 premium cars to achieve a productivity ratio of 7.
To know more about ratio visit:
https://brainly.com/question/13419413
#SPJ1
HELPP PLS need help to find answer

Answers
Area of the shape is 70 units²
We have,
The given shape is a trapezium.
The area of the trapezium.
= 1/2 x height x (sum of the [parallel sides)
Now,
Height = 7
Parallel sides = 10 and 10
So,
Area of the shape.
= 1/2 x 7 x (10 + 10)
= 1/2 x 7 x 20
= 7 x 10
= 70 units²
Thus,
The area of the shape is 70 units²
Learn more about trapezium here:
https://brainly.com/question/22607187
#SPJ1
Find the midpoint of the segment with the following endpoints.
(4, -10) and (0,0)
Answers
Answer:(2, -5)
Step-by-step explanation:
1. Which of the following triangles is classified as a right triangle?
a triangle with side lengths of 5, 12, 16
a triangle with side lengths of 10, 11, 14
a triangle with side lengths of 3, 4, 6
a triangle with side lengths of 12, 16, 20
Answers
Answer:
a triangle witih side lengths of 12,16,20
Kristen owns a bakery and is making a cake for a wedding. The dimensions of the cake are shown below. Answer each of the questions below.
What is the frosted area of the top cake? (Round to the nearest tenth)
What is the frosted area of the bottom cake? (Round to the nearest tenth)
What is the total surface area of cake that will be frosted?

Answers
Answer:
$22.5.
Step-by-step explanation:
The total revenue that is gained from the sales of the cakes is determined by multiplying the number of cakes by the price. If we let x be the number of $1 that should be deducted from the price and y be the total revenue,
y = (25 - x)(100 + 5x)
Simplifying,
y = 2500 + 25x - 5x²
We get the value of x that will give us the maximum revenue by differentiating the equation and equating the differential to zero.
dy/dx = 0 = 25 - 10x
Calculate the value for the for the following scores 20, 60, 30, 50 given:
begin inline style begin display style sum for blank of end style end style x squared =
Answers
The sum of the scores is equal to 160.
What is a mean?In Mathematics, a mean is sometimes referred to as an average and it can be defined as a ratio of the sum of the total number in a data set (population) to the frequency of the data set.
How to calculate the mean for a data set?Mathematically, the mean for this set of scores can be calculated by using the following formula:
Mean = [F(x)]/n
For the total number of scores (data set), we have;
∑x = 20 + 60 + 30 + 50
∑x = 160.
Mean = [F(x)]/n = 160/4 = 40.
Read more on mean here: brainly.com/question/9550536
#SPJ1

4
If Randy flips a coin 3 times, what is the probability that it will come up heads 3 times?
Answers
Hi there! :)
Answer:
\(P(heads) = \frac{1}{8}\)
Step-by-step explanation:
Probability of a coin landing on heads:
\(P(heads) = \frac{1}{2}\)
Find the probability of getting heads 3 times:
\(\frac{1}{2} * \frac{1}{2} * \frac{1}{2} = \frac{1}{8}\)
Therefore, the probability of the coin showing heads for 3 tosses is:
\(P(heads) = \frac{1}{8}\)
A cube has a volume of 27 cubic inches. What is the length of each edge of the cube?
Answers
Step-by-step explanation:
cube answer=3
?^3=27
3^3=27
Answer:
3x3x3
Step-by-step explanation:
Since volume is height times width times length, it would be 3x3x3=27. Hope this helps!
Question:-
The area of two similar triangles are 81 cm2 and 49 cm² respectively. If one of the sides of the first triangle is 6.3 cm, find the corresponding side of the other triangle.
Answers
Let's assume that the corresponding side of the second triangle is \(\displaystyle\sf x\).
The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides. Therefore, we can set up the following proportion:
\(\displaystyle\sf \left( \dfrac{x}{6.3} \right)^{2} =\dfrac{49}{81}\)
To find \(\displaystyle\sf x\), we can solve the proportion above:
\(\displaystyle\sf \left( \dfrac{x}{6.3} \right)^{2} =\dfrac{49}{81}\)
Taking the square root of both sides:
\(\displaystyle\sf \dfrac{x}{6.3} =\sqrt{\dfrac{49}{81}}\)
Simplifying the square root:
\(\displaystyle\sf \dfrac{x}{6.3} =\dfrac{7}{9}\)
Cross-multiplying:
\(\displaystyle\sf 9x = 6.3 \times 7\)
Dividing both sides by 9:
\(\displaystyle\sf x = \dfrac{6.3 \times 7}{9}\)
Calculating the value:
\(\displaystyle\sf x = 4.9\)
Therefore, the corresponding side of the second triangle is \(\displaystyle\sf 4.9 \, cm\).
\(\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}\)
♥️ \(\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}\)
Answer:
Step-by-step explanation:
let's assume that the corresponding side of the second triangle is .
The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides. Therefore, we can set up the following proportion:
To find , we can solve the proportion above:
Taking the square root of both sides:
Simplifying the square root:
Cross-multiplying:
Dividing both sides by 9:
Calculating the value:
Therefore, the corresponding side of the second triangle is 4.9cm
hope it helped u dear...........
During the cold winter months, a sheet of ice covers a lake near the Arctic Circle. At the
beginning despring, the ice starts to melt.
3
The variable s models the ice sheet's thickness (in meters) t weeks after the beginning of spring.
8 = -0.25t+4
By how much does the ice sheet's thickness decrease every 6 weeks?
Answers
The sheet decreased by 1.5 meters and is now at 2.5 meters.
How to illustrate the equation?An equation is the statement that illustrates the variables given. In this case, two or more components are taken into consideration to describe the scenario.
In this case, s=−0.25t + 4 represents the thickness of the ice over t weeks. To find the thickness at 6 weeks, substitute t=6.
s = -0.25(6)+4
s = 2.5 meters
It started at t= 0 at 4 meters. So it decreased by (4 - 2.5) = 1.5 meters.
The start of spring has 4 meters because when t= 0, s= -0.25(0)+4 = 4
Learn more about equations on:
https://brainly.com/question/2972832
#SPJ1
During the cold winter months, a sheet of ice covers a lake near the Arctic Circle. At the beginning of spring, the ice starts to melt.
The variable s models the ice sheet's thickness (in meters) t
weeks after the beginning of spring.
s=−0.25t+4s=-0.25t+4
s=−0.25t+4
By how much does the ice sheet's thickness decrease every 6 weeks?
The volume of the rectangular pyramid below is 56 units³. Find the value of x.
Height=7
Width=6
Length=x
Answers
The length of the rectangular pyramid is 4 units.
How to find the value of the length?For a rectangular pyramid of length L, width W, and height H, the volume is given by:
V = L*W*H/3
in this case we know that the volume is 56 cubic units, and that:
Height=7
Width=6
Length=x
Replacing all of that in the equation above we will get:
56 = x*6*7/3
56 = 14x
56/14 = x
4 = x
The length is 4 units.
Learn more about volume at:
https://brainly.com/question/1972490
#SPJ1
Plz help I need help

Answers
Determine which conic section is represented based on the given equation: 4x^2+9xy+4y^2-36y-125=0
Answers
The conic section of the equation 4x² + 9x +4y² - 36y - 125 = 0 is a circle
Selecting the conic section of the equationThe given equation is
4x² + 9xy + 4y² - 36y - 125 =0
The above equation is an illustration of a circle equation
The standard form of a circle equation is
(x - a)² + (y - b)² = r²
Where
(a, b) is the center
r is the radius
While the general form of the equation is
ax² + fx + by² + gy + c =0
Where c is a constant
Recall that, we have
4x² + 9x + 4y² - 36y - 125 =0
This is the general form
We can convert to the standard form as follows
Divide through by 4
x² + 2.25x + y² - 9y - 31.25 =0
Next, we complete the square of the x-terms and the y-terms
For the x-terms, we have
x² + 2.25x = x² + 2.25x + (2.25/2)² - (2.25/2)²
x² + 2.25x = (x + 2.25/2)² - (2.25/2)²
For the y-terms, we have
y² - 9y = y² - 9y + (9/2)² - (9/2)²
y² - 9y = (y - 9/2)² - (9/2)²
Substitute the new x and y terms
So, x² + 2.25x + y² - 9y - 31.25 = 0 becomes
(x + 2.25/2)² - (2.25/2)² + (y - 9/2)² - (9/2)²- 31.25 =0
Evaluate the sum of like terms
(x + 2.25/2)² + (y - 9/2)² - 3377/64 = 0
So, we have
(x + 9/8)² + (y - 9/2)² = 3377/64
Using the above as a guide, we can conclude that the conic section of the equation is a circle
Read more about conic section at
brainly.com/question/9702250
#SPJ1
Find the slope of the line y= -1/3x-6
Answers
Answer:
-1/3
Step-by-step explanation:
y=mx+b where m=slope and b=y-intercept.
Central High School plays Eastern High School in a basketball game. Eastern had double the score of Central before Central scored a three-pointer as the game ended.
The variable, c, represents Central's score before the three-pointer. Express the total points scored in the game as a variable expression. Check all that apply.
2c + c
3c + 3
2c + 3
2c + c – 3
2c – c + 3
2c + c + 3
Answers
What is the DOMAIN of the relationship shown here?
Write your answer in algebraic notation.
O 0
all x values
0-3
0 -3 sy 30
4
.3
-2
.
0
3
4
5
6
- 1
all y values
15
-
о
Sign out

Answers
Answer:
Step-by-step explanation:
All "x" values
x ∈ ( - ∞ , ∞ )
Absolute value -1+5 |n|=44 pls show work

Answers
Answer:
n = -9 or 9
Step-by-step explanation:
-1 + 5|n| = 44
~Add 1 to both sides
5|n| = 45
~Divide 5 to both sides
|n| = 9
~Knowing the absolute value rule, the answer can be positive or negative.
Best of Luck!
Answer:
The value of n is 9 or -9.Step-by-step explanation:
-1 + 5|n| = 44=> 5|n| = 44 + 1=> 5|n| = 45=> |n| = 45/5=> |n| = 9 or -9=> n = 9 or -9Hence, the value of n is 9 or -9.
Hoped this helped.
\(BrainiacUser1357\)
Find the value of the remaining variable in the formula. Use 3.14 as an approximation
for л (pi).
P = 2L+2W (perimeter of a rectangle); L = 9, W=7
Answers
Given:
L = 9
W = 7
Substituting these values into the formula:
P = 2(9) + 2(7)
P = 18 + 14
P = 32
Therefore, the value of the remaining variable, which is the perimeter (P) of the rectangle, is 32.
El valor de y varía directamenete con x. Si x =4 , entonces y=10 ¿cual es el valor de x y cuabdo y=25.
Answers
Answer:
el valor de x cuando y = 25 es 10
Step-by-step explanation:
If triangles ABC and DEF are similar, what is y? Show your work.

Answers
The value of y is 18
What are similar triangles?Similar triangles have the same corresponding angle measures and proportional side lengths. The angles of the two triangle must be equal and it not necessary they have equal sides.
Therefore the corresponding angles of similar triangles are congruent and the ratio of corresponding sides of similar triangles are equal.
Therefore;
14/21 = 12/y
14y = 21 × 12
14y = 252
divide both sides by 14
y = 252/14
y = 18
Therefore the value of y is 18.
learn more about similar triangles from
https://brainly.com/question/14285697
#SPJ1
What’s the domain of F(x)=|x|, g(x)=x+9 find domain for f o g
Answers
The domain of the functions F(x)=|x|, g(x)=x+9, f o g is x ∈ R the functions exist for all real numbers.
What is a function?
It is defined as a special type of relationship, and they have a predefined domain and range according to the function every value in the domain is related to exactly one value in the range.
The function f(x):
f(x) = |x|
The domain of the function is:
x ∈ R
g(x) = x + 9
The domain of the function:
x ∈ R
f o g = f(g(x)) = |x + 9|
The domain of the function f o g is x ∈ R
Thus, the domain of the functions F(x)=|x|, g(x)=x+9, f o g is x ∈ R the functions exist for all real numbers.
Learn more about the function here:
brainly.com/question/5245372
#SPJ1
X=Y+Y xy So, x=X-Y/Yy True False

Answers
The statement X = Y + Yxy is True.
The equation given is:
X = Y + Yxy
To find x = (X- Y) / Yy we have to substitute the value of x in X = Y + Yxy as
X = Y + Yxy
X = Y + Yy (X-Y) / Yy
To solve for x, we can rearrange the equation as:
X = Y + X - Y
X = X
Thus, the statement is True.
Learn more about Equation here:
https://brainly.com/question/29657983
#SPJ1
4/1=8/2,so 8 cups = quarts
Answers
Answer:
8 cups eqaul 2 quarts
Step-by-step explanation:
Consider the function f(x)=2x−−√−8. If f−1(x) is the inverse function of f(x), find f−1(2)
Answers
\(f^(-1)(2) = 6\), which is consistent with our earlier result.
What is inverse function?A function that "undoes" another function is known as an inverse function. If f(x) is a function, then f(x inverse, )'s indicated by f-1(x), is a function that accepts f(x output )'s as an input and outputs f(x initial )'s input.
Given the function f(x) = √(2x - 8), if f^(-1)(x) is the inverse function of f(x), what is \(f^(-1)(2)\)?
Solution:
To find f^(-1)(2), we need to find the value of x such that \(f(x) = 2\) . We can set up an equation:
\(f(x) = \sqrt(2x - 8) = 2\)
Squaring both sides, we get:
\(2x - 8 = 4\)
\(2x = 12\)
\(x = 6\)
Therefore, \(f^(-1)(2) = 6.\)
We can also verify this result by using the definition of an inverse function. If f^(-1)(x) is the inverse function of f(x), then by definition:
\(f(f^(-1)(x)) = x\)
We can substitute x = 2 and solve for f^(-1)(2):
\(f(f^(-1)(2)) = 2\)
\(f^(-1)(2) = (f(6))^(-1)\)
f(6) = √(2(6) - 8) = √4 = 2
Therefore,\(f^(-1)(2) = 6\), which is consistent with our earlier result.
Learn more about function here:
https://brainly.com/question/2541698
#SPJ1
what is the amount if local tax withheld on this W-2
A) $2294
B) $2340
C) $256
D) 4599

Answers
Step-by-step explanation:
the local tax is B) $2340 thats what i got
Question 6 Which of the following is the graph of f(x) = x² = 5x + 4?
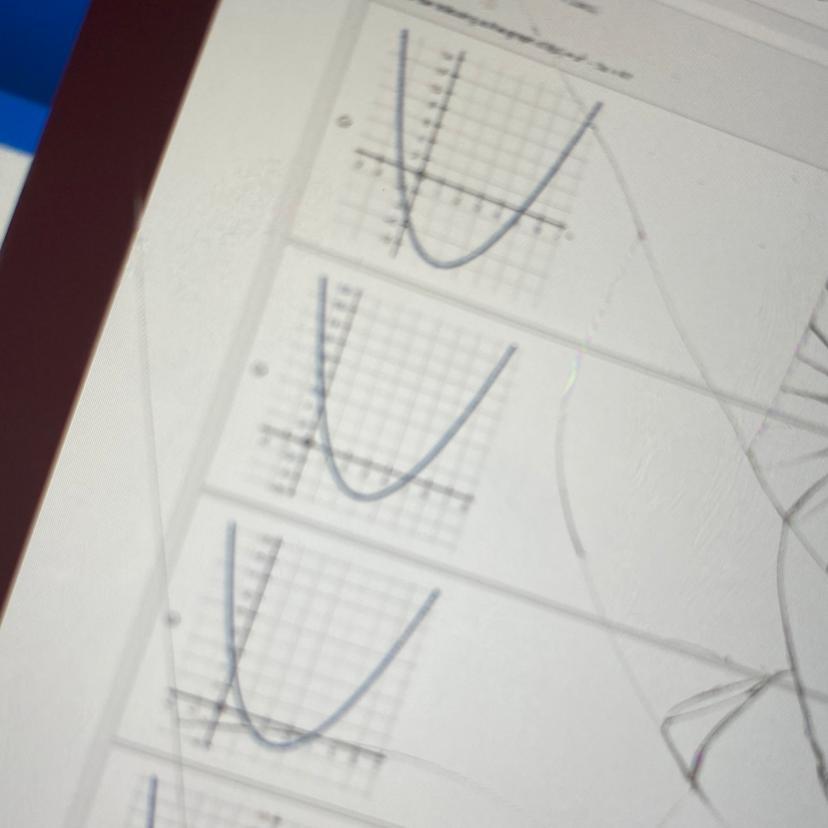
Answers
Given: The equation x² = 5x + 4
We have to draw the the graph for the given equation.
Consider the given equation,
x^2 - 5x - 4 = 0
The vertex of the parabola of the form f(x) = ax^2 + bx + c is given by x = -b/2a
Here,
a= 1
b= -5
c= -4
vertex = x = 5/2= 2.5
Also, the y coordinate at x = 2.5 is,
y = (2.5)^2 -5(2.5)-4
y = -10.25
Thus the vertex of parabola is (2.5 , -10.25)
y - intercept is the point where x = 0
put x = 0 in given equation
f(x) = 0 - 0 -4
f(x) = -4
hence y intercept is at (0, -4).
Now, we calculate x- intercept
x- intercept is where y is equal to 0.
Put f(x) = 0
We have,
x^2 - 5x - 4 = 0
by using quadratic formula,
x = -b ±√b² - 4ac/2a
x=5 ±√-5² - 4 (1)(-4)/2
x= 5±√41/2.
Hence with the obtained values the graph of the equation is obtained.
Learn more about Parabola,
https://brainly.com/question/29267743
#SPJ1