a sample of size 115 will be drawn from a population with mean 48 and standard deviation 12 . use the ti-83 plus/ti-84 plus calculator. (b) find the 25th percentile of x . round the answer to at least two decimal places. the 25th percentile is
Answers
Using the ti-83 plus/ti-84 plus calculator, the 25th percentile of x is equal to 47.25 with a mean of 48 and a standard deviation of 12, respectively.
what is mean ?A dataset's mean is calculated by dividing the sum of all values by the total number of values. The term "average" is frequently used to describe it because it is the most widely used central tendency metric.
calculation
a) µ = 48
σ = 12
n= 115
X = 45
Z =(X - µ )/(σ/√n) = (45-48)/(12/√115)= -2.68
P(X<45) = P(Z<-2.68) = 0.0037
b) µ = 48.00
σ = 12.00
n= 115.00
P(X ≤ x) = 0.2500
z value at 0.25= -0.674 (excel formula =NORMSINV(0.25))
z=(x-µ)/(σ/√n)
X=z * σ/√n +µ= -0.674*12/√115+48= 47.25
Using the ti-83 plus/ti-84 plus calculator, the 25th percentile of x is equal to 47.25 with a mean of 48 and a standard deviation of 12, respectively.
To know more about mean visit :-
https://brainly.com/question/13451489
#SPJ4
Related Questions
any one can. solve this please

Answers
Answer:
4/1 is the answer
Step-by-step explanation:
according to rules 1st divide then multiple
last addition and subtraction
HELP PLEASE
I've been working on this problem ALL DAY and I can't seem to figure it out. I know what the answer is, but I don't know how to get there.
2x^2 + 9x + 3 = 0. If r and s represent the solutions, what is r^2 + s^2?
The answer should be 17.25 but I keep getting 10.something. If you genius' out there solve this and give me a step by step breakdown, I will give brainliest!
Answers
The value of r² + s² is 17.25 if r and s represents the solution of the given quadratic equation 2x² + 9x + 3 = 0.
To find the sum of squares of the solutions of the given quadratic equation, we can use the formula
r² + s² = (r + s)² - 2rs
where r and s are the roots of the quadratic equation.
In this case, we have the equation
2x² + 9x + 3 = 0
We can use the quadratic formula to find the roots:
x = (-b ± √(b² - 4ac)) / 2a
where a = 2, b = 9, and c = 3.
Plugging in these values, we get
x = (-9 ± √(9² - 4(2)(3))) / 4
Simplifying
x = (-9 ± √69) / 4
So the roots are
r = (-9 + √69) / 4
s = (-9 - √69) / 4
To find r² + s², we need to compute (r + s)² - 2rs
(r + s)² - 2rs = ((-9 + √69)/4 + (-9 - √69)/4)² - 2((-9 + √69)/4)((-9 - √69)/4)
Simplifying
= ((-18)/4)² - 2((-9 + √69)/4)((-9 - √69)/4)
= (9/2)² - 2((81 - 69)/16)
= 81/4 - 3/2
= 69/4
= 17.25
Hence, the sum of squares of the solutions of the given quadratic equation 2x² + 9x + 3 = 0 is 17.25.
To know more about quadratic equation here
https://brainly.com/question/30098550
#SPJ1
The diameter of a circle is 7 ft. Find its area to the nearest tenth.

Answers
Given that diameter of a circle is 7 ft, its area to the nearest tenth is 38.5 square feet.
What is the area of the circle?Area of a circle is the region occupied by the circle in a two-dimensional plane. It can be determined easily using a formula, A = πr2 where r is the radius of the circle.
To find the radius, we can divide the diameter by 2: r = d/2 = 7/2 = 3.5 ft
Now we can plug this into the formula for the area:
A = πr^2
A = π(3.5)^2
A ≈ 38.48
Therefore, rounding to the nearest tenth, the area of the circle is approximately 38.5 square feet.
Read more about area
brainly.com/question/25292087
#SPJ1
Could someone help? Thanks

Answers
Answer:
x = -3, y = -0.512
x = -1, y = -3.2
x = 0, y = -8
x = 2, y = -50
Step-by-step explanation:
show that if a ⊆ c and b ⊆ d, then a × b ⊆ c × d
Answers
(x, y) is an element of the set c × d, since x is an element of c and y is an element of d.
Since (x, y) was an arbitrary element in a × b, we can conclude that every element in a × b is also in c × d. Thus, we have shown that if a ⊆ c and b ⊆ d, then a × b ⊆ c × d.
To show that if a ⊆ c and b ⊆ d, then a × b ⊆ c × d, follow these steps:
Step 1: Understand the notation.
a ⊆ c means that every element in set a is also in set c.
b ⊆ d means that every element in set b is also in set d.
Step 2: Consider the Cartesian products.
a × b is the set of all ordered pairs (x, y) where x ∈ a and y ∈ b.
c × d is the set of all ordered pairs (x, y) where x ∈ c and y ∈ d.
Step 3: Show that a × b ⊆ c × d.
To prove this, we need to show that any ordered pair (x, y) in a × b is also in c × d.
Let (x, y) be an arbitrary ordered pair in a × b. This means that x ∈ a and y ∈ b.
Since a ⊆ c, we know that x ∈ c because every element in set a is also in set c.
Similarly, since b ⊆ d, we know that y ∈ d because every element in set b is also in set d.
Now, we have x ∈ c and y ∈ d, so the ordered pair (x, y) belongs to c × d.
Step 4: Conclusion
Since any arbitrary ordered pair (x, y) in a × b also belongs to c × d, we can conclude that a × b ⊆ c × d.
Learn more about Set:
brainly.com/question/28492445
#SPJ11
What is the "Area" of 4.4mm, 3.9mm and 8.7mm
Answers
Answer:
4.4 x 3.9 x 8.7 = 149.292
To find an area multiply all given side lengths and make sure to know what shape you are finding the area too because different shapes have different formula's. Parallelograms such as square rectangle or any parallel pair will be just L x W x H or L x W depends if its 2d or 3d
A
8
B
7
D
С
CD = [?]
Enter the number that belongs in
the green box
Enter
![A8B7DCD = [?]Enter the number that belongs inthe green boxEnter](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/P4nQX9m89l4IkqZ1ouA9NYHW0yg0043p.png)
Answers
Answer:
the number that belongs in the green box is 8
What is the equation of the following graph? Use equation y = mx + b (picture included)
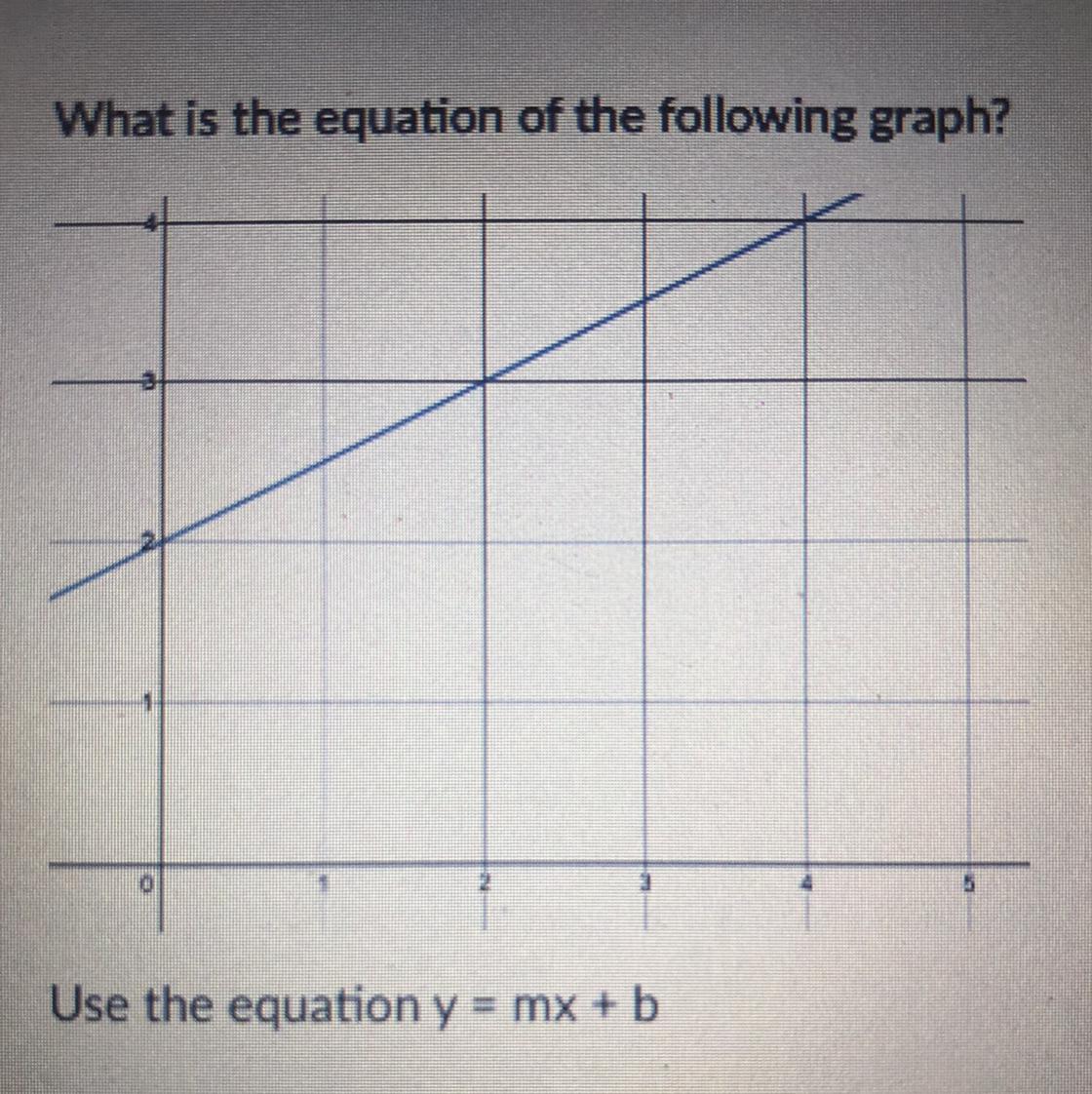
Answers
y=1/2x+2
Which function is a second-degree function? Responses A. y = xy = x B. y = 3x - 7y = 3 x - 7 C. y = x2 y = x 2 D. y = 3
Answers
In the given options, only option C has the form of a second-degree function, y = x², where a=1, b=0, and c=0.
Therefore, the correct answer is C.
What is the polynomial equation?
A polynomial equation is an equation in which the variable is raised to a power, and the coefficients are constants. A polynomial equation can have one or more terms, and the degree of the polynomial is determined by the highest power of the variable in the equation.
The function y = x² is a second-degree function because it contains a variable, x, raised to the second power.
Option A, y = x, is a first-degree function because it contains a variable, x, raised to the first power.
Option B, y = 3x - 7, is a first-degree function because it contains a variable, x, raised to the first power.
Option D, y = 3, is a constant function because it does not contain any variable raised to any power.
Therefore, the answer is option C, y = x² has the form of a second-degree function.
To learn more about the polynomial equation visit:
brainly.com/question/1496352
#SPJ1
4. In your own words describe the difference between the natural breaks, quantile, and equal interval classification schemes that can be used to make a thematic map. Refer to lecture and homework 8.
Answers
The natural breaks, quantile, and equal interval classification schemes are methods used to categorize data for the purpose of creating thematic maps. Each scheme has its own approach and considerations: Natural Breaks, Quantile, Equal Interval.
Natural Breaks (Jenks): This classification scheme aims to identify natural groupings or breakpoints in the data. It seeks to minimize the variance within each group while maximizing the variance between groups. Natural breaks are determined by analyzing the distribution of the data and identifying points where significant gaps or changes occur. This method is useful for data that exhibits distinct clusters or patterns.
Quantile (Equal Count): The quantile classification scheme divides the data into equal-sized classes based on the number of data values. It ensures that an equal number of observations fall into each class. This approach is beneficial when the goal is to have an equal representation of data points in each category. Quantiles are useful for data that is evenly distributed and when maintaining an equal sample size in each class is important.
Equal Interval: In the equal interval classification scheme, the range of the data is divided into equal intervals, and data values are assigned to the corresponding interval. This method is straightforward and creates classes of equal width. It is useful when the range of values is important to represent accurately. However, it may not account for data distribution or variations in density.
In summary, the natural breaks scheme focuses on identifying natural groupings, the quantile scheme ensures an equal representation of data in each class, and the equal interval scheme creates classes of equal width based on the range of values. The choice of classification scheme depends on the nature of the data and the desired representation in the thematic map.
Learn more about interval from
https://brainly.com/question/30460486
#SPJ11
q1.2: what power of 2 is the smallest representable positive normalized number? submit the exponent only.
Answers
The smallest representable positive number is 2149, or roughly 1.4*10-45.
Lets take a 32-bit floating point integer (IEEE 754) with the following bits,
0-22 for the mantissa (23 bits), 23-30 for the exponent ( 8 bits), and 31 for the sign (1bit)
The decimal counterpart of this expression would be if we put all zeros in the mantissa and all ones in the exponent.
The way of representing huge numbers in terms of powers is known as an exponent.
Exponent, then, is the number of times a number has been multiplied by itself. For instance, the number 6 is multiplied by itself four times, yielding 6 6 6 6. You can write this as 64. In this case, the exponent is 4 and the base is 6. This can be understood as 4 increased to the power of 6.
The exponent is represented by the symbol ^ . This symbol is known as a carrot . As an illustration, 4 raised to 2 can be expressed as 4^2 .
To learn more about exponents
brainly.com/question/5497425
#SPJ4
The diagram shows the shape of a putting green in a miniature golf course. One part of the green is a sector of a circle. To the nearest square foot, what is the area of the putting green?
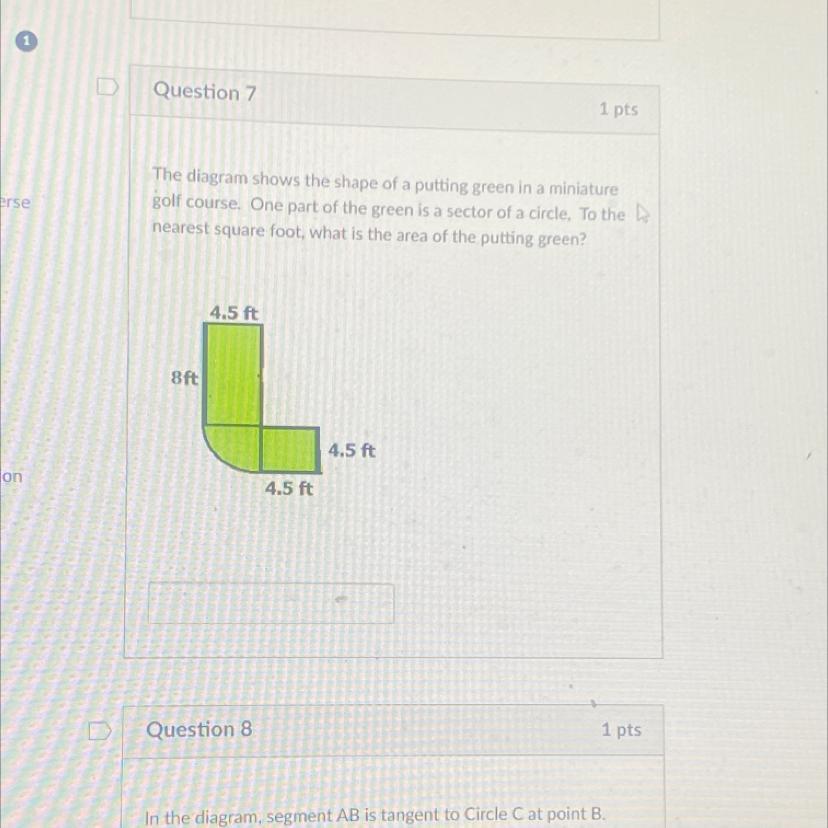
Answers
Given the diagram shows the shape of a putting green in a miniature golf course.
We will find the area of the putting green by dividing it into 3 sections as shown in the following figure:
Area (1) is the area of a rectangle with dimensions 4.5 and 8 feets
so, the area (1) = 4.5 x 8 = 36 feet²
Area (2) is the area of a square with a side length of 4.5 feet
So, the area (2) = 4.5 x 4.5 = 20.25 feet²
Area (3) is the area of the sector of a circle with a radius = 4.5 feet
The sector represents the quarter of the circle
so, Area (3) =
\(\frac{1}{4}\pi *r^2=\frac{1}{4}*\pi *4.5^2=15.9043\text{ }feet^2\)So, the total area is the sum of the three areas:
\(Total\text{ }Area=36+20.25+15.9043=72.1543\)Rounding to the nearest square foot
So, the answer will be: Area = 72 feet²

Classify the following as direct, inverse, or neither.
nf=1/2 f
Answers
The value of n for the expression nf = 1/2f will be n = 1/2.
What is an expression?The mathematical expression combines numerical variables and operations denoted by addition, subtraction, multiplication, and division signs.
Mathematical symbols can be used to represent numbers (constants), variables, operations, functions, brackets, punctuation, and grouping. They can also denote the logical syntax's operation order and other properties.
Given that the expression is nf = 1/2f. The value of n will be calculated as,
n x f = ( 1/2 ) x f
n = ( 1/2 ) x f / f
n = 1/2
The value of n in the expression nf = 1/2f is 1/2.
To know more about an expression follow
https://brainly.com/question/600196
#SPJ1
Use the Divergence Theorem to compute the net outward flux of the field F=<-x, 3y, 2z> across the surface S, where S is the boundary of the tetrahedron in the first octant formed by the plane x+y+z=1
Answers
The net outward flux across the boundary of the tetrahedron is: 5, using the concept of gradient of function.
What is the gradient of a function in a vector field?The gradient of a function is related to a vector field and it is derived by using the vector operator ∇ to the scalar function f(x, y, z).
Given vector field:
F = ( -x, 3y, 2 z )
Δ . F = (i δ/δx + j δ/δy + k δ/δz) (-x, 3y, 2 z )
Δ . F = [δ/δx(-x)] + δ/δy (3y) + δ/δz (2z)]
Δ . F = - 1 + 3 + 2
Δ . F = 4
According to divergence theorem;
Flux = ∫∫∫ Δ . (F) dv
x+y+z = 1; so, 1st octant
x from 0 to 1y from 0 to 1 -xz from 0 to 1-x-y∫₀¹∫₀¹⁻ˣ∫₀¹⁻ˣ⁻y (4) dz dy dx
= 4 ∫₀¹∫₀¹⁻ˣ (1 - x - y) dy dx
= 5
Therefore, we can conclude that the net outward flux across the boundary of the tetrahedron is: 5
To learn more about the gradient of a function refer to:
brainly.com/question/6158243
#SPJ4
Find the coordinates of point G that lies along the directed line segment from F(-1, -1) to H(-8, 20) and partitions the segment in the ratio of 5:2.
Answers
Answer:
coordinates of point g is ( -6, 14)
Step-by-step explanation:
The coordinates of the point which divides the point (x1,y1) and (x2,y2) in m:n ratio is given by (nx1+mx2)/(m+n), (ny1+my2)/(m+n).
___________________________________________
given point
F(-1, -1) to H(-8, 20)
ratio : 5:2
the coordinates of point g is
(2*-1+5*-8)/(5+2), (2*-1+5*20)/(5+2)
=> (-2 -40/7 , -2+100/7)
=> (-42/7, 98/7)
=>( -6, 14)
Thus , coordinates of point g is ( -6, 14)
Together Gabe and Dylan can paint Mrs. Gravitt's classroom in 5 hours. Gabe works twice as fast as
Dylan. How many hours would it take each of them individually to paint the room?
Answers
2 ( 3x - 1) = -6x -2
Answers
Answer:
6x -2 is the solved answer for the bracketed question.
Step-by-step explanation:
6x- 2 is not = to -6x -2
Answer: x=0
Step-by-step explanation:
if you are sloving fo x
2(3x-1) = -6x-2 cancel equal terms
6x-2=-6x-2 move the variable to the left
6x=-6x collect like terms
12x=0 divide both sides
x=0
Suppose q=ce kt satisfies the differential equation dq dt=−0. 03q. What (if anything) does this tell you about the values of c and k
Answers
This tells us that c and k must be related such that ck = -0.03.This differential equation tells us that the rate of change of q with time (dq/dt) is equal to a negative constant, -0.03.
This differential equation tells us that the rate of change of q with time (dq/dt) is equal to a negative constant, -0.03. This means that q is decreasing over time. Therefore, c and k must be related such that ck = -0.03, since this constant is the product of c and k. This tells us that c and k must be related, but does not tell us the exact value of either c or k.
Learn more about equation here
https://brainly.com/question/29657992
#SPJ4
Which of the following is equivalent to (5y + 3x) + 9x?
Answers
Answer:
12x+5y
Step-by-step explanation:
Combine 3x and 9x to get 12x.
hope it helped :)
Need help asap, thanks

Answers
Answer:
C
Step-by-step explanation:
What equation could be written for this table?

Answers
Answer:
y = 3 + 1/2 * x
Step-by-step explanation:
Help me with number three

Answers
Answer:
Volume: 16.76 cm^3
Surface area: 40.67 cm^2
Step-by-step explanation:
To find volume, you use the formula V=πr^2*h/3
To find the surface area you use formula A=πr(r+√h^2+r^2)
Answer:
V = 16.76
Surface Area = 40.67
Step-by-step explanation:
V=πr2h
A=πrl+πr2
Am I right or wrong (don't answer the last one!)

Answers
Answer:
1) Distributive Property of Multiplication (The terms are distributed)
2) Addition property of equality (Adding 14 to both sides)
3) Simplifying (We simplified the expression)
4) Division property of equality (Dividing both sides by 6)
Answer:
\(\boxed{\mathrm{view \: explanation}}\)
Step-by-step explanation:
- 14 + 6m = 10
Distributive Property of Multiplication
2 is distributed to -7 and 3m
- 14 + 14 + 6m = 10 + 14
Addition Property of Equality
Adding 14 to both sides.
6m = 24
Simplifying
Simplifying the equation.
\(\displaystyle \frac{6m}{6} =\frac{24}{6}\)
Division Property of Equality
Dividing both sides by 6.
The graph shows Manuela's earnings for the number of hours she spends tutoring.
Use the graph to answer problems 4 and 5.
How much does Manuela earn for each hour of tutoring? Explain.
Earnings ($)
100
90
80
70
60
50
40
30
20
10
0
4 6 8 10 12 14 16 18 20
Hour U
Answers
Answer:
To determine how much Manuela earns for each hour of tutoring based on the given graph, we need to look at the slope of the line. The slope represents the change in earnings for each change in hours.
From the graph, we can see that when Manuela tutors for 2 hours, she earns $20, and when she tutors for 10 hours, she earns $80. So the change in earnings is $80 - $20 = $60.
Similarly, the change in hours is 10 - 2 = 8.
Therefore, the slope of the line (representing Manuela's hourly earnings) is:
slope = change in earnings / change in hours
slope = $60 / 8
slope = $7.50/hour
Therefore, Manuela earns $7.50 for each hour of tutoring.
Find the limit. Tim (x --> 0) sin(2x)/9x
Answers
The limit of sin(2x)/(9x) as x approaches 0 is 0.Therefore lim(x → 0) sin(2x) / (9x) = 0.
To find the limit as x approaches 0 for the function sin(2x)/(9x), we'll use the limit properties and the squeeze theorem.
Step 1: Recognize the limit
The given limit is lim(x → 0) sin(2x) / (9x).
Step 2: Apply the limit properties
According to the limit properties, we can distribute the limit to the numerator and the denominator:
lim(x → 0) sin(2x) / lim(x → 0) (9x).
Step 3: Apply the squeeze theorem
We know that -1 ≤ sin(2x) ≤ 1. Dividing both sides by 9x, we get:
-1/(9x) ≤ sin(2x) / (9x) ≤ 1/(9x).
Now, as x → 0, both -1/(9x) and 1/(9x) approach 0. Therefore, by the squeeze theorem, the limit of sin(2x)/(9x) as x approaches 0 is also 0.
So, lim(x → 0) sin(2x) / (9x) = 0.
To know more about limits, visit:
https://brainly.com/question/21891582
#SPJ11
help me please do it guys

Answers
Step-by-step explanation:
Angle of four sides of rhombus is 360
125+p=360
p=360-125
p=235
hope this helps you
have a good day.
Nahla wants to rent a boat and spend at most $46. The boat costs $6 per hour, and Nahla has a discount coupon for $8 off. What are the possible numbers of hours Nahla could rent the boat?
Answers
Answer:
Nahla can rent the boat for 9 hours.
Step-by-step explanation:
Nahla has $46 and a coupon for $8 off. Which you ADD to the total that she could spend.
46 + 8 = 54
If each hour costs Nahla $6, how many hours can she rent the boat for if she has a total of $54?
54 ÷ 6 = 9
Nahla can rent the boat for 9 hours.
A small bottle of water holds 7 ounces of water. How many ounces of water do 9 bottles hold?
Answers
Step 1
Given;
\(A\text{ small bottle of water holds 7 ounces of water}\)Required; How many ounces of water do 9 bottles hold?
Step 2
To do this we will use the ratio;
\(\frac{1\text{ bottle}}{9\text{ bottles}}=\frac{7\text{ ounces}}{x}\)\(\begin{gathered} x=7(9) \\ x=63\text{ ounces} \end{gathered}\)Answer;
\(9\text{ bottles of water holds 63 ounces}\)The total cost of n shirts is $15. The shirts are priced at a constant rate of $3 each.
Which equation models this situation?
Answers
Answer:
3*x=15
Step-by-step explanation:
i think-
PLEASE HELP
In the following figure (AB) (CD). Suppose that m<1=32 (degrees). What is the m<6 ? Explain your reasoning.
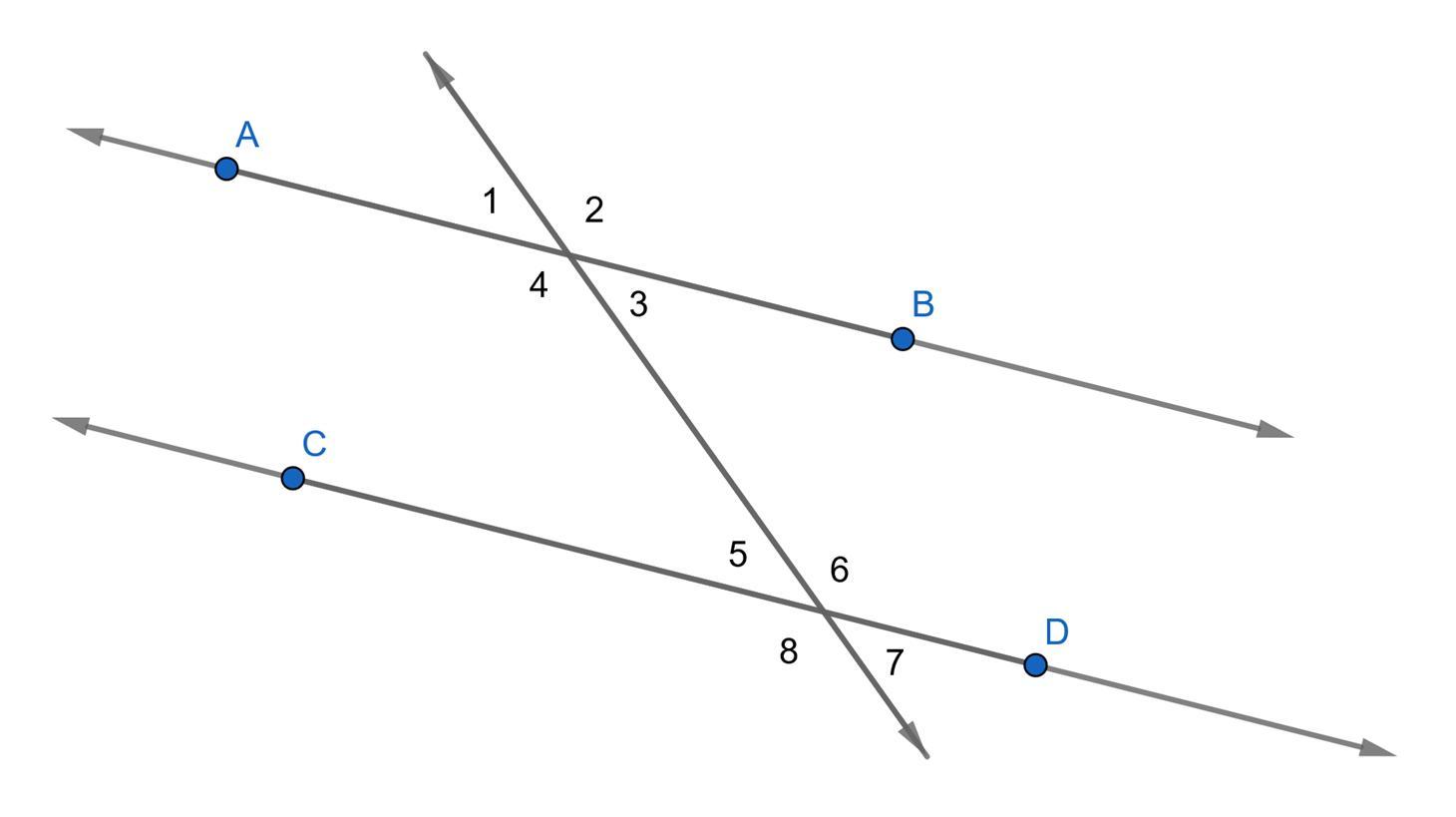
Answers
Answer:
m∠6 = 148°
Step-by-step explanation:
From the figure attached,
AB and CD are two parallel line and another transverse line is intersecting these line at two distinct points.
Since, m∠1 = 32°,
∠1 and ∠4 are supplementary angles [Linear pair of angles]
m∠1 + m∠4 = 180°
32° + m∠4 = 180°
m∠4 = 180° - 32°
m∠4 = 148°
Since, ∠4 ≅ ∠6 [Alternate interior angles]
m∠4 = m∠6 = 148°
Therefore, m∠6 = 148°
Answer:
148°Step-by-step explanation:
see attached
