A mixture is 25% red paint, 30% yellow paint, and 45%water. If 4 quarts of red paint are added to 20 quarts of the mixture, what is the percentage of red paint in the new mixture?
Answers
To make this very simple I’m going to say that initially red= 5 quarts. Add 4 to that 5 to get 9 and then divide 9 by 24. This equals .375, so you would then multiply by 100 and get 37.5%. Hope this helps you out!
Related Questions
Find the surface area of the regular pyramid.

Answers
Answer:
D
Step-by-step explanation:
It helps to break the pyramid into shapes
triangles: ((b x h) ÷ 2) x 5
((4 x 8) ÷ 2) x 5= 80in
base: 27.5in
total sa: 27.5 + 80 = 107.5in
A license plate has 7 characters. Each character can be a capital letter or a digit except for 0. How many license plates are there in which no character appears more than once and the first character is a digit?
Answers
Answer:
The number of possible license plates will be;
8,714,977,920
Step-by-step explanation:
The number of digits is 1-9 making 9
The number of alphabets is A-Z making a total 26
Number of characters is 26 + 9 = 35
Now for the 1st character
we have 9 choices
Second character, we have 34 choices since no character appear more than once
Third character, we have 33 choices
fourth 32 choices
fifth 31 choices
sixth 30 choices
seventh 29 choices
Number of possible license plates will be;
9 * 34 * 33 * 32 * 31 * 30 * 29 = 8,714,977,920
Roxy knows that she can deduct the depreciation expense of her ice cream delivery truck from her taxes over the truck’s useful life of 8 years. She can depreciate 3,100 per year. If she paid $21,000 to buy the truck, what is its salvage value?
Answers
Answer:
4,300
Step-by-step explanation:
I don’t have an explanation just trust me it’s right
How to translate equation into a sentence j + 16 = 35
Answers
Answer:
j plus sixteen is thirty-five
Step-by-step explanation:
Answer:
The sum of an unknown number and 16 gives a total of 35. find the unknown number
hope this helps
Please look at the picture and answer the question thank you

Answers
Answer:
-2x^2+5y^3+
Step-by-step explanation:
5 plus the product of 39 and a number e
Answers
The required solution is 5+39e.
What is arithmetic?
The branch of mathematics dealing with the properties and manipulation of numbers. a science that deals with the addition, subtraction, multiplication, and division of numbers. Fractions, decimals, percentages, fractions, square root, exponents, and other arithmetic operations are used to achieve mathematical simplifications
Given :
Write down the question as an algebra problem, with the unknown as X
The unknown is a number plus 5, so we write it as (X+5). The product is four times (X+5), so we write it as 39(X+5). Set it equal to e, as per the question, 5+39e
Learn more about arithmetic here:
brainly.com/question/13249066
#SPJ9
The data represents the heights of eruptions by a geyser.
Use the heights to construct a stemplot. Identify the two values that are closest to the middle when the data are sorted in order from lowest to highest.

Answers
The values nearest to these middle elements are 60 and 63 inches.
The dataset is given as:
62 33 50 90 80 50 40 70 50 63 74 53 55 64 60 60 78 70 43 82
Then, we sort the information elements in ascending request
33 40 43 50 50 50 53 55 60 60 62 63 64 70 70 74 78 80 82 90
The length of the dataset is 20.
Thus, the elements at the middle are the tenth and the 11 elements.
From the arranged dataset, these elements are: 60 and 62
Thus, the values nearest to this median are 60 and 63
to know more about the median click here:
https://brainly.com/question/14532771
#SPJ1
In March of 2018, a survey asked 801 US adults whether they had at least one subscription to a video-streaming service. Of the 801 participants in the survey, 457 indicated they subscribed to at least one video-streaming service. What is the correct 95 percent confidence interval for the proportion of all US adults who would say they subscribe to a video-streaming service?
Answers
Answer:
The 95% confidence interval for the proportion of all US adults who would say they subscribe to a video-streaming service is (0.5362, 0.6048).
Step-by-step explanation:
In a sample with a number n of people surveyed with a probability of a success of \(\pi\), and a confidence level of \(1-\alpha\), we have the following confidence interval of proportions.
\(\pi \pm z\sqrt{\frac{\pi(1-\pi)}{n}}\)
In which
z is the zscore that has a pvalue of \(1 - \frac{\alpha}{2}\).
Of the 801 participants in the survey, 457 indicated they subscribed to at least one video-streaming service.
This means that \(n = 801, \pi = \frac{457}{801} = 0.5705\)
95% confidence level
So \(\alpha = 0.05\), z is the value of Z that has a pvalue of \(1 - \frac{0.05}{2} = 0.975\), so \(Z = 1.96\).
The lower limit of this interval is:
\(\pi - z\sqrt{\frac{\pi(1-\pi)}{n}} = 0.5705 - 1.96\sqrt{\frac{0.5705*0.4295}{801}} = 0.5362\)
The upper limit of this interval is:
\(\pi + z\sqrt{\frac{\pi(1-\pi)}{n}} = 0.5705 + 1.96\sqrt{\frac{0.5705*0.4295}{801}} = 0.6048\)
The 95% confidence interval for the proportion of all US adults who would say they subscribe to a video-streaming service is (0.5362, 0.6048).
Prove that the only automorphism of a well-ordered set is the identity?
Answers
The only automorphism of a well-ordered set is the identity.
To prove this statement, we need to show that any automorphism of a well-ordered set must be the identity function. An automorphism is a bijective function that preserves the order structure of the set.
Assume we have a well-ordered set (W, ≤), where W is the set and ≤ is the order relation.
Let f: W → W be an automorphism of the set.
We aim to prove that f is the identity function, i.e., f(x) = x for all x ∈ W.
Suppose, for contradiction, that there exists an element a ∈ W such that f(a) ≠ a.
Since f is a bijective function, there must exist some b ∈ W such that f(b) = a.
Since (W, ≤) is well-ordered, there is a least element c in the set {x ∈ W : f(x) ≠ x}.
Let d = f(c). Since f is an automorphism, f(c) ≠ c, and thus d ≠ c.
Since (W, ≤) is well-ordered, there is a least element e in the set {x ∈ W : f(x) = d}.
Consider the element f(e). Since f is a bijective function, there must exist some f^{-1}(f(e)) = e' ∈ W such that f(e') = f(e) = d.
By the definition of automorphism, f(f^{-1}(y)) = y for all y ∈ W. Applying this property to e', we have f(f^{-1}(f(e'))) = f(e') = d.
However, f^{-1}(f(e')) = e' ≠ c, and thus f(e') ≠ d. This contradicts the fact that e is the least element in the set {x ∈ W : f(x) = d}.
Therefore, our assumption that there exists an element a such that f(a) ≠ a is false.
Since we assumed f(a) ≠ a for arbitrary a ∈ W, it follows that f(x) = x for all x ∈ W.
Hence, the only automorphism of a well-ordered set is the identity function.
Therefore, we have proven that the only automorphism of a well-ordered set is the identity function.
For more such questions on automorphism, click on:
https://brainly.com/question/30894112
#SPJ8
write inequality shown y=-11/7x-4
Answers
Answer:The inequality represented by the equation y = -11/7x - 4 can be written as:
y ≤ -11/7x - 4
This represents a less than or equal to inequality, indicating that the values of y are less than or equal to the expression -11/7x - 4.
Step-by-step explanation: .
Two cyclists start from 98 miles apart and begin racing toward each
other. Three hours later, they have not yet met and the distance between
them is 2 miles. How fast is each of them biking if one bikes 3 mph
slower than the other?
Answers
We want to find the velocities of two cyclists in the given situation.
The velocity of one cyclist is 17.5 mi/h, and the velocity of the other cyclist is -14.5 mi/h.
The information that we have is that:
The cyclists start from 98 miles apart.After 3 hours, they are 2 miles apart.One of them has a speed 3 mph slower than the other.Let's say that cyclist 1 starts in the position 0 and has a velocity v₁.
Then the position equation of cyclist 1 is:
p₁(t) = v₁*t
Now cyclist 2 starts at the position 98 miles, and has a velocity v₂, then we can write the position equation of cyclist 2 as:
p₂(t) = v₂*t + 98mi
Assuming that cyclist 2 is the slower one, we can write:
v₂ = -(v₁ - 3mi/h)
Where the negative sign comes because they move in opposite directions.
Then the position equation becomes:
p₂(t) = -(v₁ - 3mi/h)*t + 98mi
Then we know that after 3 hours they are 2 miles apart, then we can write:
p₂(3h) - p₁(3h) = 2mi
Then we need to solve:
-(v₁ - 3mi/h)*3h + 98mi - (v₁*3h) = 2mi
(-6h)*v₁ + 9mi + 98mi = 2mi
(-6h)*v₁ + 107mi = 2mi
(-6h)*v₁ = 2mi - 107mi = -105mi
v₁ = -105mi/(-6h) = 17.5 mi/h
So the velocity of cyclist 1 is 17.5 mi/h
And the velocity of cyclist 2 is:
v₂ = -(17.5 mi/h - 3mi/h) = -14mi/h.
If you want to learn more, you can read:
https://brainly.com/question/11549992
cuanto tiempo le demorará a juan doblar su depósito de $500.00al 9% de interés simple?
Answers
SIMPLE INTREST = P X NX R/100
P= 500 ,N=?, R=9%
AMOUNT WILL ONLY GET DOUBLE WHEN INTREST EQUALS TO DEPOSIT.
SI=500
\(on\text{ solving,500=500}\ast9\ast\frac{n}{100}-\longrightarrow\text{ n=100/9}\)n=100/9
n=11.11
so it will take about 11.11 years
The answer is 11.11 years
Write and solve an inequality to find the possible values of x.

Answers
The inequality tha calculates the possible values of x is x < 2
How to determine the inequality tha calculates xFrom the question, we have the following parameters that can be used in our computation:
The figure
Where, we have
3x + 2 < 10
And, we have
2x + 6 < 10
Evaluate the expressions
So, we have
3x < 8 and 2x < 4
Evaluate
x < 8/3 and x < 2
Hence, the inequality tha calculates x is x < 2
Read more about inequality at
https://brainly.com/question/32124899
#SPJ1
Solve the equation: 3x - 2/4 = 2x – 8 Explain your reasoning / show work:
Answers
Reduce the fraction
Move terms
Collect like terms and calculate
A marketing company wanted to test what makes people purchase more cereal and they varied box size and flashy/simple graphics. Which of the following would be the main effects tested in this study? a. the results comparing each box size and comparing flashy vs Simple graphics b. behavior of purchasing cereal c. the results comparing each box size only d. the results comparing flashy vs. simple graphics only
Answers
Option A is correct that is the results comparing each box size and comparing flashy vs simple graphics.
Given this, a marketing firm tested several package variations, including size, complexity, and simplicity, to determine which would encourage customers to buy more cereal.
Which of the following would be the key conclusions of the study?
We are aware of this since we are comparing various box and graphic sizes.
When contrasting the sizes of each box and the flashy vs. simple images, the influence of the research can be noticed.
The comparison of the sizes of each box and the effectiveness of flashy vs. straightforward images shows that Option A is the best choice.
To learn more about graphics visit: https://brainly.com/question/29082830
#SPJ4
Write x^2 - 8x + 10 in the form
(x + a)^2 + B
Answers
\(x^2-8x+10=x^2-8x+16-6=(x-4)^2-6\)
ab-c/d has a value of 24. write the values if :-
1- a, b, c, d are all positive.
2- a, b, c, d are all negative.
3- a, b, c, d are mixed of negative and positive.
WRITE ANSWERS FOR 1, 2 AND 3
Answers
The values of ab, b - c, and c/d are 6, -1, and 4 respectively when a = 2, b = 3, c = 4 and d = 1.Using BODMAS rule, we can simplify the given expression.ab - c/d = 24
Given ab-c/d has a value of 24.Now, we have to find the value ofab, b - c, and c/d.Multiplying d on both sides, we getd(ab - c/d) = 24dab - c = 24d...(1)Now, we can find the value of ab, b - c, and c/d by substituting different values of a, b, c and d.Value of ab when a = 2, b = 3, c = 4 and d = 1ab = a * b = 2 * 3 = 6.
Value of b - c when a = 2, b = 3, c = 4 and d = 1b - c = 3 - 4 = -1Value of c/d when a = 2, b = 3, c = 4 and d = 1c/d = 4/1 = 4Putting these values in equation (1), we get6d - 4 = 24dSimplifying, we get-18d = -4d = 2/9
For more such questions on BODMAS rule
https://brainly.com/question/28832666
#SPJ8
Find the unit rate (constant of proportionality) of the distance traveled.
Number of hours
0.25 1.5 2.5 3
Distance traveled (km) 3 18 30 36
Answers
Answer:
12.
Step-by-step explanation:
if to re-write the given condition, then
\(\frac{3}{0.25} =\frac{18}{1.5} =\frac{30}{2.5} =\frac{36}{3} ;\)
it is clear, the required constant is 12 (12 per hour).
Factorise 2 + x^3 - 3x^6
answer is (2 + 3x^3)(1 - x)(1 + x + x^2)
need working out
Answers
Let w = x^3
Square both sides to find that w^2 = (x^3)^2 = x^(3*2) = x^6
In short: w^2 = x^6
The given expression 2+x^3-3x^6 turns into 2+w-3w^2 and rearranges into -3w^2+w+2
Set this equal to zero and use the quadratic formula. We'll plug in
a = -3b = 1c = 2So,
\(w = \frac{-b\pm\sqrt{b^2-4ac}}{2a}\\\\w = \frac{-1\pm\sqrt{(1)^2-4(-3)(2)}}{2(-3)}\\\\w = \frac{-1\pm\sqrt{25}}{-6}\\\\w = \frac{-1\pm5}{-6}\\\\w = \frac{-1+5}{-6} \ \text{ or } \ w = \frac{-1-5}{-6}\\\\w = \frac{4}{-6} \ \text{ or } \ w = \frac{-6}{-6}\\\\w = -\frac{2}{3} \ \text{ or } \ w = 1\\\\\)
If w = -2/3, then that rearranges to the following
w = -2/3
3w = -2
3w+2 = 0
This makes (3w+2) a factor of -3w^2+w+2
If w = 1, then it rearranges to w-1 = 0.
This makes (w-1) a factor of -3w^2+w+2
--------------------
To summarize the previous section, we found the factors of -3w^2+w+2 were:
(3w+2)(w-1)It leads to (3w+2)(w-1)
We must stick a negative out front because the leading coefficient is negative.
Therefore, -3w^2+w+2 = -(3w+2)(w-1)
You can use the FOIL rule to confirm.
--------------------
Recall we made w = x^3
Let's replace each w with x^3
-(3w+2)(w-1)
-(3x^3+2)(x^3-1)
This tells us that 2+x^3-3x^6 factors to -(3x^3+2)(x^3-1)
The next task is to factor x^3-1 using the difference of cubes factoring rule.
a^3 - b^3 = (a-b)(a^2 + ab + b^2)
x^3 - 1^3 = (x-1)(x^2 + x*1 + 1^2)
x^3 - 1 = (x-1)(x^2 + x + 1)
--------------------
So,
2+x^3-3x^6
-3x^6 + x^3 + 2
-(3x^3+2)(x^3-1)
-(3x^3+2)(x-1)(x^2 + x + 1)
-(2 + 3x^3)(-(1-x))(1 + x + x^2)
(2 + 3x^3)(1 - x)(1 + x + x^2)
Take careful notice that x-1 turned into -(1-x) in the 3rd step. The negative out front for -(1-x) cancels out with the original negative out front.
Hi guys can someone help me with this fast? Find the distance between each pair of points
Thanks!

Answers
Answer:
there are 3 ways to answer this and I don't know which way you teacher wants it so I have included sqare root, simplified square root, and rounded four decimal places
I also counted to the points since they were not included (also I forgot to put the - in front of the 2 of (-6,-2) but I did put it in the equation)

The list below shows the scores for each of Sarah’s homework assignments.
100, 95, 47, 83, 87, 89, 89
If the score 47 is removed from the list, which of the following statements is true
Answers
The correct statement regarding the mean of the data-set when the score of 47 is removed is given as follows:
The mean increased by about 6.
How to calculate the mean of a data-set?The mean of a data-set is given by the sum of all observations in the data-set divided by the number of observations, which is also called the cardinality of the data-set.
The observations for this problem are given as follows:
100, 95, 47, 83, 87, 89, 89.
There are 7 observations, and their sum is given as follows:
100 + 95 + 47 + 83 + 87 + 89 + 89 = 590.
Hence the mean is of:
590/7 = 84.29.
Removing the observation of 47, there will be 6 observations, with a sum of 590 - 47 = 543, hence the mean is of:
543/6 = 90.5.
Meaning that the mean increases by about 6.
More can be learned about the mean of a data-set at https://brainly.com/question/1136789
#SPJ1
If the perimeter of the rectangle below is cut in half, what is the area of the new rectangle?
No links, docs, files, drives etc
I will mark the correct answer brainlyest
You earn many points

Answers
For what value of A is the function, (x), continuous at x=0?

Answers
(i) \(\lim_{x \to \frac{\pi^-}{2}}\) h(x) = 3
(ii) \(\lim_{x \to \frac{\pi^+}{2}}\) h(x) = -1
(iii) h(0) = 1/7
The value of λ must be 7, for h(x) to be continuous at x = 0.
The given function is,
h(x) = 1/7, when x = 0
= 1 - 2 cos 2x, when x < π/2
= 1 + 2 cos 2x, when x > π/2
= x cos x/sin λx, when x < 0
Now,
(i) \(\lim_{x \to \frac{\pi^-}{2}}\) h(x) = \(\lim_{x \to \frac{\pi^-}{2}}\) (1 - 2 cos 2x) = 1 - 2 cos π = 1 + 2 = 3
(ii) \(\lim_{x \to \frac{\pi^+}{2}}\) h(x) = \(\lim_{x \to \frac{\pi^+}{2}}\) (1 + 2 cos 2x) = 1 + 2 cos π = 1 - 2 = -1
(iii) h(0) = 1/7
Since the function is continuous at x = 0, so
\(\lim_{x \to 0}\) h(x) = h(0)
\(\lim_{x \to 0}\) x cos x/sin λx = 1/7
\(\lim_{x \to 0}\) cos x.\(\lim_{x \to 0}\) 1/λ(sinλx/λx) = 1/7
1/λ = 1/7
λ = 7
Hence the value of λ must be 7.
To know more about continuous here
https://brainly.com/question/30089268
#SPJ1
Of the at-home games, what proportion of games were wins? (Note: Some answers are rounded to two decimal places
Answers
Answer:
0.33
Step-by-step explanation:
See comment for complete question
Given
\(H = 60\%\)
\(W=25\%\)
\(HW = 20\%\) --- at-home wins
Required
The proportion of at-home games that were wins
This proportion is represented as:
\(Pr = HW : H\)
Substitute values for HW and H
\(Pr = 20\% : 60\%\)
Divide by 20%
\(Pr = 1 : 3\)
Express as fraction
\(Pr = 1 /3\)
\(Pr = 0.33\)
A house is on an 80,000 sq. ft lot. About how many acres is the lot? There are 43.560 square feet in a acre?
Answers
6. Maggie works at The Drug Store five days a week. Last week, she worked a
total of 35 hours. She worked the same number of hours every day, except
Saturday, when she worked 11 hours. How many hours did she work on the
other days?
Answers
Answer: 7
and maybe 5.83
Step-by-step explanation:
If she worked 5 days a week, and worked the same hours of those days, then the answer is 7. You simply divide 35/5 which gives you that answer. And they’ve already given you the answer for Saturday, so yeah.
But you did say she only worked 5 days a week—in 35 hours. And you also said “how many hours did she work on the other days”. If Saturday’s hours was already stated, then are you implying she worked for 6 days instead of 5? Because there’s 7 days a week and if Saturday is unaccounted for, then she worked 6 days. In that case, your answer would be 5.83.
I need the answer please

Answers
Answer:
\( \frac{x - 9}{2} = 5 \\ x - 9 = 5 \times 2 \\ x = 10 + 9 \\ x = 19\)
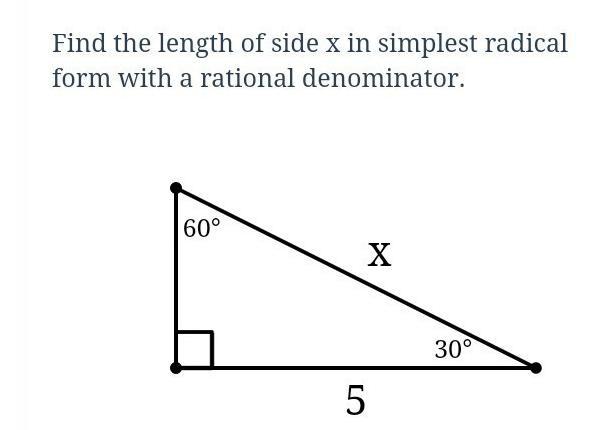
Find the length of side X in simple radical form with a rational denominator
Answers
The length of side X in simple radical form with a rational denominator is 25/√3.
What is a 30-60-90 triangle?In Mathematics and Geometry, a 30-60-90 triangle is also referred to as a special right-angled triangle and it can be defined as a type of right-angled triangle whose angles are in the ratio 1:2:3 and the side lengths are in the ratio 1:√3:2.
This ultimately implies that, the length of the hypotenuse of a 30-60-90 triangle is double (twice) the length of the shorter leg (adjacent side), and the length of the longer leg (opposite side) of a 30-60-90 triangle is √3 times the length of the shorter leg (adjacent side):
Adjacent side = 5/√3
Hypotenuse, x = 5 × 5/√3
Hypotenuse, x = 25/√3.
Read more on 30-60-90 triangle here: brainly.com/question/30283450
#SPJ1
Missing information:
The question is incomplete and the complete question is shown in the attached picture.
simplify 4 times 18 over 6 times 5 over 5
A. 12 B. 0 C. 60 D. 3
Answers
Answer:
c.60
Step-by-step explanation:
What is 50% of 20?.........................
Answers
Answer:
10
Step-by-step explanation:
50%, or 1/2 of 20 is 10.
Answer:
10!
Step-by-step explanation:
50% is half, so half of 20 is 10!