A factory uses a special kind of lubricant to maintain its four milling machines. The weekly lubricant usage for each machine can be approximated with a normal distribution. This distribution has a mean of 30 gallons and a standard deviation of 11.5 gallons, and it can be considered as an independent random variable (zero covariance, zero correlation) from machine to machine. Suppose at the beginning of the week, the factory has a total of 150 gallons of lubricant in stock. The factory will not receive any replenishment of lubricant from its supplier until the end of the week.Assume that the total lubricant usage (four machines combined) also follows a normal distribution.
Required:
What is the probability that the factory will run out of lubricant before the next replenishment arrives?
Answers
Answer:
0.0968 = 9.68% probability that the factory will run out of lubricant before the next replenishment arrives
Step-by-step explanation:
When the distribution is normal, we use the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the zscore of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.
This distribution has a mean of 30 gallons and a standard deviation of 11.5 gallons
Since there are four machines, we have that:
\(\mu = 30*4 = 120\)
\(\sigma = 11.5\sqrt{4} = 11.5*2 = 23\)
What is the probability that the factory will run out of lubricant before the next replenishment arrives?
More than 150 gallons, so this is 1 subtracted by the pvalue of Z when X = 50.
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{150 - 120}{23}\)
\(Z = 1.3\)
\(Z = 1.3\) has a pvalue of 0.9032
1 - 0.9032 = 0.0968
0.0968 = 9.68% probability that the factory will run out of lubricant before the next replenishment arrives
Related Questions
Part I: A secant is a line or segment thatpasses through a circle in two places. In thediagram above, find the m< ACE which isformed by two secants.1. Determine the method of finding themACE by circling one of the statementsbelow.2. Use the relationship you established inpart 1 to find the m
Answers
To answer this question we will use the two secants theorem, the two secants theorem states:
\(angle\text{ formed by two secants=}\frac{1}{2}(diffrence\text{ betw}een\text{ the arcs formed).}\)Therefore, we can establish the following relationship:
\(m\angle ACE=\frac{m\hat{AE}-m\hat{DB}}{2}\text{.}\)Substituting the given values for the arcs, we get:
\(m\angle ACE=\frac{110^{\circ}-45^{\circ}}{2}=32.5^{\circ}.\)To determine m\(m\angle BAD=\frac{1}{2}(45^{\circ}-0^{\circ})=22.5^{\circ}.\)
Answer:
\(\begin{gathered} m\angle ACE=\frac{m\hat{AE}-m\hat{DB}}{2}, \\ m\angle ACE=32.5^{\circ}, \\ m\angle BAD=22.5^{\circ}. \end{gathered}\)find the surface area
Answers
The Surface area of Triangular Prism is 132 cm².
We have have the dimension of prism as
Sides = 3 cm, 4 cm, 5 cm
and, l = 10 cm
and, b= 4 cm
Now, Surface area of Triangular Prism as
= (sum of sides) l + bh
= (3 + 4 + 5)10 + 4 x 3
= 12 x 10 + 12
= 120 + 12
= 132 cm²
Thus, the Surface area of Triangular Prism is 132 cm².
Learn more about Surface Area here:
https://brainly.com/question/29298005
#SPJ1
If a certain number x is multiplied by 6
It will be equal to four less than twice
the same number?
Answers
Answer: x= -1
Step-by-step explanation: 6x = 2x-4 4x= -4 and x=-1
From the given statement the unknown number is found to be - 1
The given statements can written in algebraic form as follows;
the unknown number = x
the number is multiplied by 6 = 6x
four less than twice the same number = 2x - 4
then, from the given statement the final equation equation becomes;
6x = 2x - 4
This unknown number can be solved by collecting similar terms together;
6x - 2x = -4
4x = -4
divide through by 4
\(\frac{4x}{4} = \frac{-4}{4} \\\\x = -1\)
Thus, the unknown number is - 1
Learn more here: https://brainly.com/question/24369824
Simplify.
- 2x - } – 5x + i + x
-
х
-
17/3
-
3
+
10
х
Enter your answer in the box.
Do not use decimals in your answer.
Answers
Answer:
I'dont think it's 77 or not right
Given info:-
Evaluate:
[(1⅕ - 2/5).(-3/5)³]÷(-9)
⇛[6/5 - 2/5).(3³/5³)]÷(-9)
Take the LCM 5 & 5 is 5.
⇛[(6-2 /5). (3*3*3/5*5*5)]÷(-9)
⇛[(4/5).(27/125)]÷(-9)
⇛[4/5 × 27/125)]÷(-9)
⇛[(4*27)/(5*125)]÷(-9)
⇛[20/625] ÷ (-9)
⇛[20/625] ÷ 1/9
⇛20/625 × 9/1
⇛(20*9)/(625*1)
⇛180/625
Now, reduce the fraction by extracting and cancaling out with 5.
⇛36/125 or 0.228 Ans.
Hope this helps!
Tree heights: Cherry trees in a certain orchard have heights that are normally distributed with mean μ = 112 inches and standard deviation σ = 10 inches. Use the TI-84 PLUS calculator to answer the following. Round the answers to at least two decimals. (a) Find the 22nd percentile of the tree heights. (b) Find the 80th percentile of the tree heights. (c) Find the first quartile of the tree heights. (d) An agricultural scientist wants to study the tallest 1% of the trees to determine whether they have a certain gene that allows them to grow taller. To do this, she needs to study all the trees above a certain height. What height is this? Part: 0 / 40 of 4 Parts Complete Part 1 of 4 Find the 22nd percentile of the tree heights. The 22nd percentile of tree heights is inches.
Answers
Answer:
Explained below.
Step-by-step explanation:
Let X represents the tree heights.
It is provided that X follows a normal distribution with mean μ = 112 inches and standard deviation σ = 10 inches.
(a)
Compute the 22nd percentile of the tree heights as follows:
\(P(X<x)=0.22\\\\P(Z<z)=0.22\)
The z-score for the corresponding probability is, z = -0.77.
Compute the value of x as follows:
\(z=\frac{x-\mu}{\sigma}\\\\-0.77=\frac{x-112}{10}\\\\x=112-(0.77\times 10)\\\\x=104.3\)
Thus, the 22nd percentile of the tree heights is 104.3 inches.
(b)
Compute the 80th percentile of the tree heights as follows:
\(P(X<x)=0.80\\\\P(Z<z)=0.80\)
The z-score for the corresponding probability is, z = 0.84.
Compute the value of x as follows:
\(z=\frac{x-\mu}{\sigma}\\\\0.84=\frac{x-112}{10}\\\\x=112+(0.84\times 10)\\\\x=120.4\)
Thus, the 80th percentile of the tree heights is 120.4 inches.
(c)
Compute the first quartile of the tree heights as follows:
\(P(X<x)=0.25\\\\P(Z<z)=0.25\)
The z-score for the corresponding probability is, z = -0.67.
Compute the value of x as follows:
\(z=\frac{x-\mu}{\sigma}\\\\-0.67=\frac{x-112}{10}\\\\x=112-(0.67\times 10)\\\\x=113.3\)
Thus, the first quartile of the tree heights is 113.3 inches.
(d)
The tallest 1% of the trees, i.e. P (X > x) = 0.01.
That is, P (X < x) = 0.99.
⇒ P (Z < z) = 0.99
The corresponding z-value is, z = 2.33.
Compute the value of x as follows:
\(z=\frac{x-\mu}{\sigma}\\\\0.99=\frac{x-112}{10}\\\\x=112+(0.99\times 10)\\\\x=121.9\)
Thus, the tallest 1% of the trees are more than 121.9 inches tall.
What is the slope of the line passing through the points (2,
-5) and (4, 1)?
Answers
The slope of the line passing through the points (2,-5) and (4, 1) is 3.
What is a Slope of a line?The ratio of the change in the y-coordinate to the change in the x-coordinate is known as the slope in mathematics. Δy and Δx are used to represent both the net change in the y-coordinate and the net change in the x-coordinate, respectively.The formula for the change in y-coordinate with respect to the change in x-coordinate is as a resultm = Δy/Δx = change in y/change in x
where "m" represents a line's slope.
Given, the points of the line are (2, -5) and (4, 1).
Now, to calculate the slope of the line passing through the two points.
Using the formula, one may get the slope of the line connecting the points
Slope, m = y₂ - y₁ / x₂ - x₁
So, m = ( 1 - (-5)) / (4 - 2)
= 6/2
= 3
So, the slope of the line is 3.
To know more about the slope of a line visit:
https://brainly.com/question/16180119
#SPJ9
I think it’s 40%, am I correct?
Answers
my thought process is
There are 100 ticks (20 spaces with 5 marks)
the area it wants has 6 large spaces (6*5=30) and 3 marks
30+3 is 33
Sawyer got a gift card for his birthday and
wants to use it for a new video game. The game
costs $60, but his gift card only covers 50% of
that. His mom agrees to cover the rest, but says
he must pay the money back in three weeks.
How much does he have to pay each week if he
pays the same amount each week?
Answers
Answer:
Sawyer has to pay $10 each week to pay his mom back
Step-by-step explanation:
Sawyer got a gift card that he wants to use to purchase a video game that costs $60, but he can only cover 50% of it, that is, $30.
The remaining $30 will be covered by his mom, given he pays the money back in three weeks.
If he pays the same amount each week, then each week he should pay $30 / 3 = $10
Sawyer has to pay $10 each week to pay his mom back
Is 2y=4x proportional
Answers
please answer! will give brainliest
Answers
Answer:
1.4
Step-by-step explanation:
Dancing Pools sells swimming pools in 4 sizes. The small pool is 72 feet
long and 18 feet wide. The medium pool is 80 feet long and 20 feet wide. The
large pool is 88 by 22. If the new superduper Coffeetable pool is 96 feet long,
how wide will it be?
Answers
9514 1404 393
Answer:
24 ft
Step-by-step explanation:
Adding 8 ft to the length adds 2 ft to the width. The largest pool is 8 ft longer than the next-largest, so is expected to be 2 ft wider.
22 ft + 2 ft = 24 ft
The Coffeetable pool is expected to be 24 ft wide.
Answer:
24
Step-by-step explanation:
Because the wideness of the pool increase by 2 feet wide whenever the size of the increases
The rectangle below has the dimensions:
5.3 × 5.7
Create another rectangle that is scaled to 4
times the size of the current rectangle.
Answers
Answer:
A rectangle of 10.6 x 11.4 dimensions.
Step-by-step explanation:
(5.3*2)*(5.7*2)=5.3*4*5.7=10.6x11.4.
In circle O O, O P = 2 OP=2 and the length of ⌢ = 7 9 π PQ ⌢ = 9 7 π. Find the area shaded below. Express your answer as a fraction times π π.
Answers
The measure of angle POQ is given as follows:
30º.
What is the area of a circle?The area of a circle of radius r is given by π multiplied by the radius squared, as follows:
A = πr²
The radius of the circle in this problem is given as follows:
r = OP = 2.
(distance of the center O to point P on the circumference).
Hence the area of the circle is given as follows:
A = 4π.
The area of the sector is given as follows:
π/3.
The ratio of the area of the sector and the area of the circumference is given as follows:
(π/3)/(4π) = 1/12.
The entire area has a measure of 360º, hence the angle measure is obtained as follows:
1/12 x 360 = 30º.
Missing InformationThe problem is given by the image presented at the end of the answer.
More can be learned about angle measures at https://brainly.com/question/25716982
#SPJ1
One hundred samples of five data points were randomly selected from each of four populations. The medians of each population's samples were plotted as shown below. Another random sample was then taken from one of the populations and recorded as follows:
{1, 20, 5, 0, 5}
From which population was this sample MOST likely selected?
A. Population A
B. Population B
C. Population C
D. Population D
Answers
The population from which the sample was most likely selected is given as follows:
A. Population A.
How to obtain the population from which the data was most likely selected?To look at the population from which the samples were most likely selected, we look at the medians for each interval.
In a box and whisker plot, the median is the middle point between the bars of the data-set.
The sample taken is given as follows:
{1, 20, 5, 0, 5}
The sample can be ordered as follows:
0,1, 5, 5 and 20.
The median of the sample is the middle term, which is of 5.
The medians for each population are given as follows, from the box and whisker plots:
Population A: 5.Population B: 10.Population C: 15.Population D: 20.Due to the median of 5, the sample was most likely taken from Population A, and the first option is correct.
More can be learned about box and whisker plots at https://brainly.com/question/3473797
#SPJ1
Answer:
population a
Step-by-step explanation:
if the sum of the interior Angele measures of a convex ploygon is 2.60 how many sides does the polygon have?
Answers
Answer:
The polygon has 14 sides.
Explanation:
Given that the sum of the interior angles of the polygon is 2,160.
\(T=2,160\)Recall that the sum of interior angles of a polygon can be calculated using the formula;
\(\begin{gathered} T=180(n-2) \\ \text{where;} \\ n=\text{ number of sides} \\ T=\text{ sum of the interior angles of the polygon.} \end{gathered}\)Substituting the value of T, to solve for n;
\(\begin{gathered} 2,160=180(n-2) \\ \frac{2160}{180}=n-2 \\ 12=n-2 \\ n=12+2 \\ n=14 \end{gathered}\)Therefore, the polygon has 14 sides.
The rear windshield wiper of a car rotated 120 degrees,as shown. Find the area cleared by the wiper. 25inch,120 degrees, 14inch
Answers
The rear windshield wiper of a car rotated 120 degrees, as shown in the figure. The area cleared by the wiper blade is approximately 205.875 square inches.
The problem states that a car’s rear windshield wiper rotates 120 degrees, as shown in the figure. Our aim is to find the area cleared by the wiper.
The wiper's arm is represented by a line segment and has a length of 14 inches.
The wiper's blade is perpendicular to the arm and has a length of 25 inches.
Angular degree measure indicates how far around a central point an object has traveled, relative to a complete circle. A full circle is 360 degrees, and 120 degrees is a third of that.
As a result, the area cleared by the wiper blade is the sector of a circle with radius 25 inches and central angle 120 degrees.
The formula for calculating the area of a sector of a circle is: A = (θ/360)πr², where A is the area of the sector, θ is the central angle of the sector, π is the mathematical constant pi (3.14), and r is the radius of the circle.
In this situation, the sector's central angle θ is 120 degrees, the radius r is 25 inches, and π is a constant of 3.14.A = (120/360) x 3.14 x 25²= 0.33 x 3.14 x 625= 205.875 square inches, rounded to the nearest thousandth.
Therefore, the area cleared by the wiper blade is approximately 205.875 square inches.
For more such questions on area, click on:
https://brainly.com/question/25292087
#SPJ8
find the missing coordinate of p, using the fact that p lies on the unit circle in the given quadrant. ( , -7/25) is in the 4th quadrants
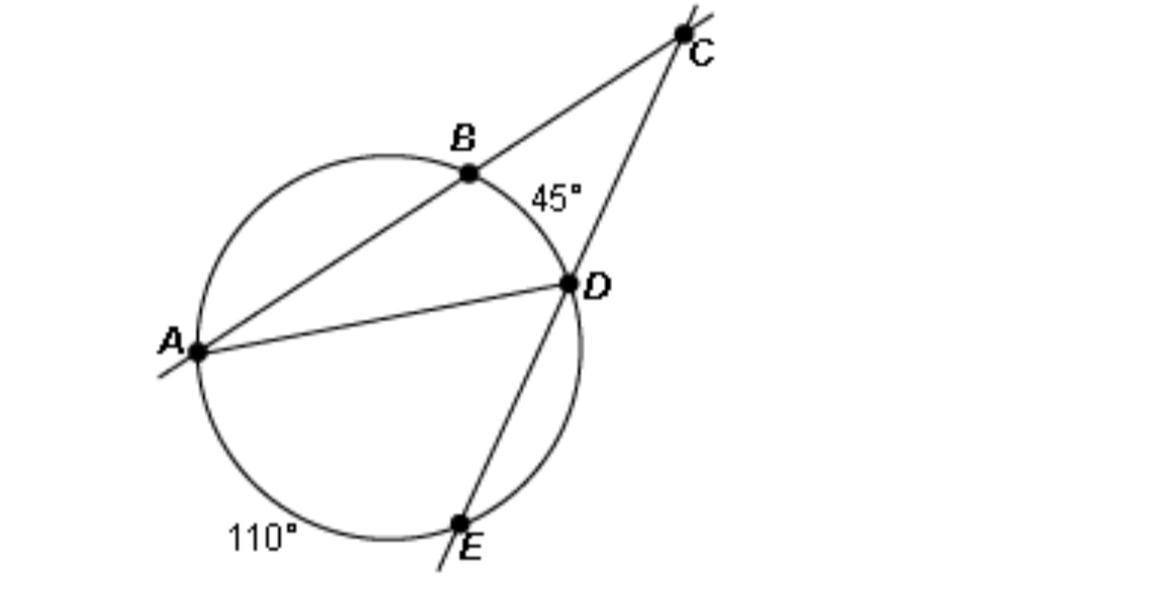
Answers
The missing x coordinate is (24/25).
What is a Circle ?
A circle is a closed, two-dimensional object where every point in the plane is equally spaced from a central point. The line of reflection symmetry is formed by all lines that traverse the circle.
As per the given data:
p lies on the unit circle
radius of circle = 1 unit
p is in 4th quadrant:
Let's assume p as (x, (-7/25))
equation of the circle:
x² + y² = 1
x² + (-7/25)² = 1
x² = 1 - (49/625)
x² = (576/625)
x = ± 24/25
But as point is in 4th quadrant, x will be positive.
x = (24/25)
The coordinate of point p is ((24/25), (-7/25))
To learn more on circles, click:
brainly.com/question/29142813
#SPJ1
A circle has center (3, -5) and the point (-1, -8) lies on the circumference of the circle. What is the equation of the circle in Standard Form?
Answers
Answer:
\( {(x - 3)}^{2} + {(y + 5)}^{2} = {5}^{2} \)
Step-by-step explanation:
First find the radius
Which is the distance between the 2 points.
Radius =5
The answer in the standad form is above.
The equation of the circle in Standard Form is (x - 3)² + (y + 5)² = 25
The standard equation of a circle is given as:
(x - a)² + (y - b)² = r²
where (a, b) is the center of the circle and r is the radius of the circle.
Given the center as (3, -5) hence the radius of the circle is the distance between (3, -5) and (-1, -8). Hence:
\(Radius=\sqrt{(-8-(-5))^2+(-1-3)^2} \\\\Radius=5\ units\\\)
hence:
(x - 3)² + (y - (-5))² = 5²
(x - 3)² + (y + 5)² = 25
The equation of the circle in Standard Form is (x - 3)² + (y + 5)² = 25
Find out more at: https://brainly.com/question/13658927
Fifteen percent of 168
Answers
Answer:
25.2
Step-by-step explanation:
168 x .15 = 25.2
\(\large\text{Hey there!}\)
\(\rm{15\%\ of\ 168}\\\\\rm{= 15\% \times 168} \\\\\rm{= \dfrac{15}{100}\times 168}\\\\\rm{= \dfrac{15}{100}\times \dfrac{168}{1}}\\\\\rm{=\dfrac{15\times168}{100\times1}}\\\\\rm{= \dfrac{2,520}{100}}\\\\\rm{= 25.2}\)
\(\huge\text{Therefore, your answer should be: }\)
\(\huge\boxed{\frak{25.2}}\huge\checkmark\)
\(\huge\text{Good luck on your assignment \& enjoy your day!}\)
~\(\frak{Amphitrite1040:)}\)
Need help in this plssss
Answers
Answer:
Store #1
Step-by-step explanation:
I buy 4 5/8 blue fabric and 2 1/8 green fabric how much blue than green did i buy
Answers
Answer:
2.5
Step-by-step explanation:
We Know
You buy 4 5/8 blue fabric and 2 1/8 green fabric .
4 5/8 = 37/8 = 4.625 blue fabric
2 1/8 = 17/8 = 2.125 green fabric
How much blue than green did you buy?
We Take
4.625 - 2.125 = 2.5
So, you buy 2.5 blue more than green.
Question:-
The area of two similar triangles are 81 cm2 and 49 cm² respectively. If one of the sides of the first triangle is 6.3 cm, find the corresponding side of the other triangle.
Answers
Let's assume that the corresponding side of the second triangle is \(\displaystyle\sf x\).
The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides. Therefore, we can set up the following proportion:
\(\displaystyle\sf \left( \dfrac{x}{6.3} \right)^{2} =\dfrac{49}{81}\)
To find \(\displaystyle\sf x\), we can solve the proportion above:
\(\displaystyle\sf \left( \dfrac{x}{6.3} \right)^{2} =\dfrac{49}{81}\)
Taking the square root of both sides:
\(\displaystyle\sf \dfrac{x}{6.3} =\sqrt{\dfrac{49}{81}}\)
Simplifying the square root:
\(\displaystyle\sf \dfrac{x}{6.3} =\dfrac{7}{9}\)
Cross-multiplying:
\(\displaystyle\sf 9x = 6.3 \times 7\)
Dividing both sides by 9:
\(\displaystyle\sf x = \dfrac{6.3 \times 7}{9}\)
Calculating the value:
\(\displaystyle\sf x = 4.9\)
Therefore, the corresponding side of the second triangle is \(\displaystyle\sf 4.9 \, cm\).
\(\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}\)
♥️ \(\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}\)
Answer:
Step-by-step explanation:
let's assume that the corresponding side of the second triangle is .
The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides. Therefore, we can set up the following proportion:
To find , we can solve the proportion above:
Taking the square root of both sides:
Simplifying the square root:
Cross-multiplying:
Dividing both sides by 9:
Calculating the value:
Therefore, the corresponding side of the second triangle is 4.9cm
hope it helped u dear...........
The flat rate for your service runs $9.50 per hour. To cover costs, you charge the flat rate plus 15% of that rate for the first 8 hours, and 10% of that rate on the second 8 hours. You estimate that a particular job will take 16 hours.
Answers
Answer:
9.50x 4=38
3x10=30 + 2x4 =38
so 10 deliveries
Step-by-step explanation:
N
2) A sample of size n= 49 is obtained. The population mean
is m= 80 and the population standard deviation is s = 14.
Find the probability that the sample has a sample average
between 78.3 and 85.1, (5 points)
-
Answers
Answer:
0.7969
Step-by-step explanation:
Given that: A sample of size n= 49 is obtained. The population mean is m= 80 and the population standard deviation is s = 14.
The z score measures the number of standard deviation by which the raw sore is above or below the mean. It is given by the equation:
\(z=\frac{x-m}{\frac{s}{\sqrt{n} } }\)
For x = 78.3, the z score is:
\(z=\frac{x-m}{\frac{s}{\sqrt{n} } }=\frac{78.3-80}{\frac{14}{\sqrt{49} } } =-0.85\)
For x = 85.1, the z score is:
\(z=\frac{x-m}{\frac{s}{\sqrt{n} } }=\frac{85.1-80}{\frac{14}{\sqrt{49} } } =2.55\)
P(78.3<x<85.1) = P(-0.85<z<2.55) = P(z<2.55) - P(z<-0.85) = 0.9946 - 0.1977 = 0.7969
Answer:
P(78.3 < x' < 85.1) = 0.7969
Step-by-step explanation:
Given:
Sample size, n = 49
mean, u = 80
Standard deviation \( \sigma \) = 14
Sample mean, ux' = population mean = 80
Let's find the sample standard deviation using the formula:
\( \sigma \bar x = \frac{\sigma}{\sqrt{n}} \)
\( = \frac{14}{\sqrt{49}} = \frac{14}{7} = 2 \)
To find the probability that the sample has a sample average between 78.3 and 85.1, we have:
\( P(78.3 < \bar x < 85.1) = \frac{P[(78.3 -80)}{2} < \frac{(\bar x - u \bar x)}{\sigma \bar x} < \frac{(85.1 -80)}{2}] \)
= P( -0.85 < Z < 2.55 )
= P(Z < 2.55) - P(Z <-0.85 )
Using the standard normal table, we have:
= 0.9946 - 0.1977 = 0.7969
Approximately 0.80
Therefore, the probability that the sample has a sample average between 78.3 and 85.1 is 0.7969
5. Write the division problem as a
multiplication equation with a
missing factor. The find the quotient.
2.1 /0.7
Answers
The quotient in this division problem is 3,4.
What is division problem?
There are three main parts to a division problem that are -the dividend, the divisor, and the quotient. The dividend is the number that will be the divided. The division is the number of (people )that the the number is being divided by among And The quotient is the answer.
a division is a process of a splitting a specific of amount into the equal parts.
Sol-
The formula is -
a/b=?
b×?=a
We can write a division statement as a multiplication statment
12/4=3
4×3=12
Thus
The quotients in this division problem are 3 and 4.
To learn more about division problem click-
https://brainly.com/question/25289437
#SPJ9
Winnie wrote the following riddle: I am a number between 60 and 100. My ones digit is two less than my tens digit. I am a prime number. What humber does Winnie's riddle describe? Explain.
Answers
Answer:
the answer is 97
Step-by-step explanation:
because 97 is between 60 and 100, 7 is less than 9, and it is a prime number. it couldn't be 64 because 64 is even, making it a composite number. it also couldn't be 75 because 75 is divisible by 5. it couldn't be 86 because 86 is divisible by 2. 97 is the only one left.
a X/a2.=a4 , find the missing exponent (x)
Answers
Remember
when you have a division of two number with exponents,let the base and subtract the exponents
\(\frac{a^m}{a^n}=a^{m-n}\)Step 1
\(\begin{gathered} \frac{a^x}{a^2}=a^4 \\ it\text{ is} \\ \frac{a^x}{a^2}=a^{x-2}=a^4 \end{gathered}\)then
\(x-2=4\)Step 2
solve for x
\(\begin{gathered} x-2=4 \\ \text{add 2 in both sides} \\ x-2+2=4+2 \\ x=6 \end{gathered}\)therefore, the missing exponent is 6
12. The calculation of property tax is based on the
Answers
The tax revenue generated from property taxes is often used to fund expressions public services such as schools, parks, and infrastructure projects in the local community.
what is expression ?In mathematics, you can multiply, divide, add, or subtract. An expression is constructed as follows: Number, expression, and mathematical operator A mathematical expression is made up of numbers, variables, and functions (such as addition, subtraction, multiplication or division etc.) It is possible to contrast expressions and phrases. An expression or algebraic expression is any mathematical statement that has variables, integers, and an arithmetic operation between them. For example, the expression 4m + 5 has the terms 4m and 5, as well as the provided expression's variable m, all separated by the arithmetic sign +. The calculation of property tax is typically based on the assessed value of the property and the tax rate set by the local government. The assessed value is determined by a government-appointed assessor who evaluates the value of the property based on factors such as its location, size, age, and condition. The tax rate is then applied to the assessed value to determine the amount of tax owed by the property owner. The tax revenue generated from property taxes is often used to fund public services such as schools, parks, and infrastructure projects in the local community.
To know more about expressions visit :-
https://brainly.com/question/14083225
#SPJ1
8) John wishes to make a line
plot of the heights in inches for a soccer team. The heights are
listed below. How many dots
would be above the greatest
height recorded?
Answer options
1
2
3
4
Answers
There are three dots in the greatest height recorded.
We have,
From the table,
We see that,
The greatest height is 75 inches.
The lowest height is 62 inches.
Now,
If we make a line plot with dots above the height as:
* *
* * * * *
* * * * *
62 66 68 72 75
Thus,
There are three dots in the greatest height recorded.
Learn more about line plots here:
https://brainly.com/question/29573088
#SPJ1
At first an athlete jogs at 5 miles per hour and then jogs at 8 miles per hour traveling 11 miles in 1.6 hours. How long does the athlete jog at each speed? (Hint: Lett represent the amount of time the athlete jogs at 5 mph. Then 1.6 - t represents the amount of time the athlete jogs at 8 mph)
Answers
Answer:
15
Step-by-step explanation: