a convex mirror, like the passenger-side rearview mirror on a car, has a focal length of -2.8 m. an object is 5.6 m from the mirror.
Answers
The image's distance from the mirror is -1.87, by using the mirror equation.
Note:- Although the question is missing, I believe the issue is asking where the image is located.
To find the solution to the problem, the mirror equation can be used:
Mirror equation = \(\frac{1}{f}+\frac{1}{d_{o} }+\frac{1}{d_{i} }\)
Where,
f = mirror's focal length
\(d_{o}\) = object's distance from the mirror
\(d_{i}\) = image's distance from the mirror
The focal length is assumed to be negative for a convex mirror in our problem.
f = -2.8 m
The object's distance (do) = 5.6m
By using the mirror equation, the image's distance from the mirror can be determined
\(\frac{1}{f}+\frac{1}{d_{o} }+\frac{1}{d_{i} }\)
i.e, \(\frac{1}{d_{i} } = \frac{1}{f} -\frac{1}{d_{o} }\)
= \(-\frac{1}{2.8} -\frac{1}{5.6}\) = \(-\frac{3}{5.6}\)
= - 0.5357
\(d_{i} =\) \(-\frac{5.6}{3}\)
= -1.87 m
The virtual nature of the image is indicated by the negative sign (located behind the mirror)
To know more about Convex mirror visit here:
https://brainly.com/question/27518252
#SPJ4
Related Questions
For each equation below, determine if the given value is a solution or not. 12- x= x, x = 3
Answers
Answer:
no that is not a solution
Step-by-step explanation:
12-x=x or 12-3=3 is not a solution because the answer doesnt make the equation
The length of the sides of the triangle are in the ratio 3:4:5 and it’s perimeter is 144 cm find its area and height corresponding to the longest side
Answers
144 = 3x + 4x + 5x (combine like terms)
144 = 12x (divide both sides by 12)
x = 12
To find the side lengths, multiply 3, 4 and 5 by 12. This means the triangle has sides of 36, 48 and 60 centimetres.
Because this is a right triangle, two of the sides are the base and the height. The hypotenuse (longest side) is not the base nor the height because it is not directly adjacent to the right angle. In this case, the hypotenuse is 60 cm.
A = bh/2
A = (36 cm)(48 cm)/2
A = 864 cm^2
Therefore the area is 864 cm^2.
I’m not sure what is meant by the “height corresponding to the longest side”, sorry.
Hope this helps!
what is x for 3 = x+2
Answers
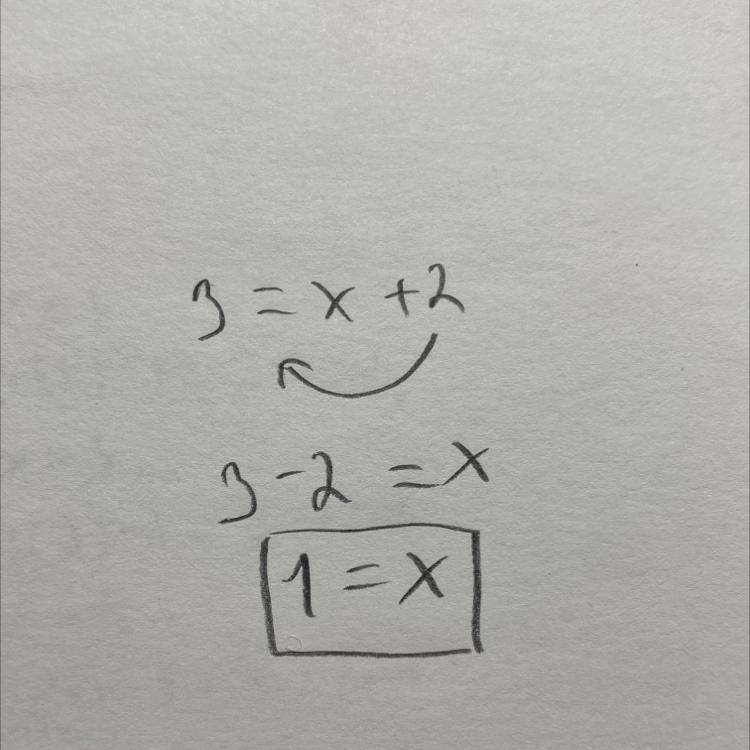
Answer: 4x - 2 = 3x + 1
Your welcome you can thank me later <3
Write the equation of the circle with the given information.
Center: (5, -13)
Radius: 11
Answers
Answer:
(x - 5)² + (y + 13)² = 121
Step-by-step explanation:
The equation of a circle in standard form is
(x - h)² + (y - k)² = r²
where (h, k) are the coordinates of the centre and r is the radius
Here (h, k ) = (5, - 13 ) and r = 11 , then
(x - 5)² + (y - (- 13))² = 11² , that is
(x - 5)² + (y + 13)² = 121
-8/9 + (-2)/57
find the absolute value of the following rational number
Answers
The absolute value of the Rational number -474/513 is 474/513.
To find the sum of the rational numbers -8/9 and -2/57, you need to have a common denominator. The least common multiple (LCM) of 9 and 57 is 513. So, you can rewrite the fractions with a common denominator:
-8/9 = (-8/9) * (57/57) = -456/513
-2/57 = (-2/57) * (9/9) = -18/513
Now, you can add the fractions:
-456/513 + (-18/513) = (-456 - 18)/513 = -474/513
To find the absolute value of the rational number -474/513, you simply ignore the negative sign and take the value as positive:
| -474/513 | = 474/513
Therefore, the absolute value of the rational number -474/513 is 474/513.
For more questions on Rational .
https://brainly.com/question/30339525
#SPJ8
How do you write equations in Point-slope form?
Answers
For a line with a slope a and a known point (h, k), the point-slope form is:
y = a*(x - h) + k
How to write an equation in point slope form?A general linear equation can be written in slope-intercept form as:
y = a*x + b
Where a is the slope and b is the y-intercept.
If we know that a line passes through a point (h, k), then the point-slope form of that line is:
y = a*(x - h) + k
Notice that particularly, the y-intercept can be written as (0, b), then the slope-intercept form is also a point-slope:
y = a*(x - 0) + b
y = a*x + b
Learn more about linear equations by reading:
https://brainly.com/question/1884491
#SPJ1
HELP ME PLEASE!!!!!!!!!!!!

Answers
1) The three main trigonometric ratios of the given triangle are:
sin B = 5/9.43
cos B = 8/9.43
tan B = 5/8
2) The measure of angle A is: ∠A = 39.6°
3) The length of side x is: x = 39.5 mm
How to find the trigonometric ratios?The six trigonometric ratios of a right angle triangle are:
sin x = opposite/hypotenuse
cos x = adjacent/hypotenuse
tan x = opposite/adjacent
cot x = 1/tan x
sec x = 1/cos x
cosec x = 1/sin x
1) The three main trigonometric ratios of the given triangle are:
sin B = 5/9.43
cos B = 8/9.43
tan B = 5/8
2) The measure of angle A is gotten from:
∠A = cos⁻¹ (47/61)
∠A = 39.6°
3) The length of side x using trigonometric ratios is:
21/x = tan 28
x = 21/tan 28
x = 39.5 mm
Read more about Trigonometric ratios at: https://brainly.com/question/13276558
#SPJ1
Evaluate. 1 1/2+3/4÷(−1/3)−2/3 Enter your answer as a mixed number in simplest form
Answers
Answer:
-1 5/12
Step-by-step explanation:
1 1/2+3/4÷(−1/3)−2/3
3/2-2/3+3/4*3/-1
9-4/6-9/4
5/6-9/4
20-54/24
-34/24
-17/12
-1 5/12
Find the function with the given derivative whose graph passes through the point P.r'(theta)=9+sec^2(theta), P(pi/4,2)
Answers
The given derivative is:
\(r^{\prime}(\theta)=9+\sec ^2\theta\)Integrate w. r. t. theta to get:
\(\begin{gathered} r(\theta)=\int (9+\sec ^2\theta)d\theta \\ =9\int d\theta+\int \sec ^2\theta d\theta \end{gathered}\)Use the formulae given by:
\(\int d\theta=\theta+c,\int \sec ^2\theta d\theta=\tan \theta+c\)To get the solution as follows:
\(r(\theta)=9\theta+\tan \theta+c\)The given point is P(pi/4,2) so it follows:
\(\begin{gathered} 2=9(\frac{\pi}{4})+\tan \frac{\pi}{4}+c \\ 2-\frac{9\pi}{4}-1=c \\ c=1-\frac{9\pi}{4} \end{gathered}\)Substitute the value to get the required answer as follows:
\(r(\theta)=9\theta+\tan \theta+1-\frac{9\pi}{4}\)The above function is the required answer.
The height h of an object thrown from the top of a ski lift 1240 feet high after t seconds is h=-16t2 +32t+1240. For what times is the height of the object at least 1000 feet?
←
The height of the object is at least 1000 feet from seconds to seconds.
Answers
Check the picture below.
so the parabolic path of the object is more or less like the one shown below in the picture, now this object has an initial of 1240 ft, as it gets thrown from the ski lift, so from 0 seconds is already higher than 1000 feet.
\(h=-16t^2+32t+1240\hspace{5em}\stackrel{\textit{a height of 1000 ft}}{1000=-16t^2+32t+1240} \\\\\\ 0=-16t^2+32t+240\implies 16t^2-32t-240=0\implies 16(t^2-2t-15)=0 \\\\\\ t^2-2t-15=0\implies (t-5)(t+3)=0\implies t= \begin{cases} ~~ 5 ~~ \textit{\LARGE \checkmark}\\ -3 ~~ \bigotimes \end{cases}\)
now, since the seconds can't be negative, thus the negative valid answer in this case is not applicable, so we can't use it.
So the object on its way down at some point it hit 1000 ft of height and then kept on going down, and when it was above those 1000 ft mark happened between 0 and 5 seconds.

If y=5x-3and 3x-y=-1, what is the value of y?
A. 7
B. -1
C. 2
D. -8
Answers
Draw a quick picture to find the product of 3×800
Answers
Answer:
daymn
it's gonna be okay
On a standardized exam, the scores are normally distributed with a mean of 300 and a standard deviation of 40. Find the z-score of a person who scored 300 on the exam.
Answers
A z-score of 0 indicates that the person's score is equal to the mean, so they are right at the Average Performance level.the z-score of a person who scored 300 on the exam is 0.
The z-score of a person who scored 300 on the exam, we can use the formula:
z = (x - μ) / σ
where z is the z-score, x is the raw score, μ is the mean, and σ is the standard deviation.
In this case, the person scored 300 on the exam, which is equal to the mean (μ). Therefore, we can substitute these values into the formula:
z = (300 - 300) / 40
Simplifying the equation, we have:
z = 0 / 40
Since any number divided by zero is undefined, we can conclude that the z-score of a person who scored 300 on the exam is 0.
The z-score measures the number of standard deviations a data point is away from the mean. In this case, a z-score of 0 indicates that the person's score is equal to the mean, so they are right at the average performance level.
To know more about Performance .
https://brainly.com/question/29807565
#SPJ11
What is the constant in 12r + r/2-19
Answers
Answer:
constant is - 19
Step-by-step explanation:
the constant is the term in an expression with no variable attached to it.
12r + \(\frac{r}{2}\) - 19
the only term without the variable r attached to it is - 19
then the constant term is - 19
Nikhil and Mae work at the same company. Nikhil has been at the company 4 time+s as long as Mae. Nikhil's time at the company is 8 more than 2 times Mae's time. The following system of equations models the scenario: x = 4y x = 8 + 2y How many years has each person been employed by the company? Nikhil has been with the company for 16 years, while Mae has been there for 4 years. Nikhil has been with the company for 24 years, while Mae has been there for 6 years. Nikhil has been with the company for 20 years, while Mae has been there for 5 years. Nikhil has been with the company for 12 years, while Mae has been there for 3 years
Answers
Applying the system of equations given, we can conclude that: a. Nikhil has been with the company for 16 years, while Mae has been there for 4 years.
How to Apply a System of Equations?To solve the system of equations, let's substitute the value of x from the first equation into the second equation:
x = 4y
8 + 2y = 4y
Simplifying the equation, we get:
8 = 2y
Dividing both sides by 2:
4 = y
Now, substitute the value of y back into the first equation to find x:
x = 4y
x = 4(4)
x = 16
Therefore, Nikhil has been employed by the company for 16 years, and Mae has been employed for 4 years.
The correct answer is option a. Nikhil has been with the company for 16 years, while Mae has been there for 4 years.
Learn more about System of Equations on:
https://brainly.com/question/13729904
#SPJ1
Ian took out a $19,000 personal loan to pay for his home renovations. He will not make a payment for 5 years and there is a 15% interest rate. How much will be owed in 5 years with monthly compounding?
Round your answer to the nearest cent.
Do NOT round until your final answer.
Answers
The amount owed in 5 years with monthly compounding, considering a $19,000 personal loan with a 15% interest rate, will be $34,558.52.
1. Convert the interest rate to a decimal: 15% = 0.15.
2. Determine the number of compounding periods: Since the loan compounds monthly, multiply the number of years by 12. In this case, 5 years * 12 months/year = 60 months.
3. Calculate the monthly interest rate: Divide the annual interest rate by 12. In this case, 0.15 / 12 = 0.0125.
4. Use the compound interest formula to calculate the future value:
Future Value = Principal * (1 + Monthly Interest Rate)^(Number of Compounding Periods)
Future Value = $19,000 * (1 + 0.0\(125)^{(60\))
5. Evaluate the expression inside the parentheses: (1 + 0.0\(125)^{(60\)) ≈ 1.954503.
6. Multiply the principal by the evaluated expression: $19,000 * 1.954503 = $37,133.57 (unrounded).
7. Round the final answer to the nearest cent: $34,558.52.
Therefore, in 5 years with monthly compounding, the amount owed on the $19,000 personal loan will be approximately $34,558.52.
For more such questions on interest rate, click on:
https://brainly.com/question/25720319
#SPJ8
HELPP PLSS What is the volume of the triangular prism?
A) 180 cm3
B)360 cm3
C) 720 cm3
D)1440 cm3

Answers
Answer: D. 1440cm
Step-by-step explanation:
volume=lengthxwidthxheight
8x15x12=1440
rewrite 5-6 using the additive inverse and display the help this are the answers

Answers
Answer:
Additive inverse of (5-6) is (6-5),
------------------------------
So:
(5-6)+(6-5)=0
5-6+6-5=0
5-6=-6+5
-------------------------
Left <--- -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6 ---> Right
Move 5 places to the right of -6 and you should land on -1.
How can the system of equation be represented in a matrix 3x−2y=−25, 5x−2y=−39
?
Answers
Answer:
{x,y}={7,-2}
Step-by-step explanation:
3x - 2y = 25
-5x + 2y = -39
[2] 2y = 5x - 39
[2] y = 5x/2 - 39/2
// Plug this in for variable y in equation [1]
[1] 3x - 2•(5x/2-39/2) = 25
[1] -2x = -14
// Solve equation [1] for the variable x
[1] 2x = 14
[1] x = 7
4) During a school carnival, students from the middle school raised money by selling crafts, food, game tickets, and school play admissions. Of each dollar earned, $0.15 came from games. Craft sales earned 3 times as much as games. Food sales were 4 times the amount earned from the play.
Crafts-blank
Play-blank
Games-$0.15
Food-$0.32
If the total sales were $500, then:
How much was earned from the craft sales?
How much was earned from the play?
Answers
$225 was earned from the craft sales
and $40 was earned from the play.
Given, During a school carnival, students from the middle school raised money by selling crafts, food, game tickets, and school play admissions.
Of each dollar earned, $0.15 came from games. Craft sales earned 3 times as much as games. Food sales were 4 times the amount earned from the play.
Let the amount earned by play be x,
Now, Games earned = 0.15×500 = $75
Also, crafts earned 3×75 = $225
Now, as play earned x, then food earned 4x.
According to question,
x + 75 + 225 + 4x = 500
5x + 300 = 500
5x = 200
x = 40
So, the amount earned by Play be, $40
and the amount earned by Food be $160.
Hence, $225 was earned from the craft sales
and $40 was earned from the play.
Learn more about Linear Equations here https://brainly.com/question/24085666
#SPJ1
what is f(g(13)) ? A mapping diagram is shown.
Answers
Answer:
im about 90% sure its 32
Step-by-step explanation:
Can someone please help me? Thank you

Answers
Answer:
A=1/2PA
Step-by-step explanation:
DO THE FORMULA
15+16+17+24 = 72
area of rectangle is length x width
15x16=240
area of triangle is base x height divide by 2
8x15=120
120 divide by 2 is 60
add 240 and 60 to give you 300
Please help it’s due tomorrow

Answers
Answer:
Step-by-step explanation:

The ships were 4000miles apart at midnight and were headed directly toward each other. if they collided at 8 am, find the speed of both ships if one was 20 miles per hour faster.
Answers
Answer:
The slower ship is going 240 mph
The faster ship is going 260 mph
Step-by-step explanation:
midnight to 8 am is 8 hours, the distance shortened between the ships each hour was 500 miles so if the slower ship's speed is x and the faster ship's speed is y:
x + y = 500
and the question tells us that
x + 20 = y
Using the substitution method we can substitute the y in the first question for the second's.
x + (x + 20) = 500
solve:
x + x + 20 = 500
2x + 20 = 500
2x + 20 - 20 = 500 - 20
2x = 480
(2x) / 2 = 480 / 2
x = 240
Now that we have x we can now substitute the x into the second equation
(240) + 20 = y
260 = y
y = 260
And after adding the unit of measurement (Miles Per Hour) we get the speed of the slower ship (x) to be 240 MPH, and the speed of the faster ship (y) to be 260 MPH.
Jamie's family has completed 80% of a trip. They have traveled 40 miles. How far is the trip?
Answers
Answer:
50
Step-by-step explanation:
because forty is eighty percent of 50
A box contains 54 coins which are either 20-cent coins or 50-cent coins. If the total value of all the coins is $20.70, find the number of 20-cent coins in the box. LOF 1 11.
Answers
Number of 20-cent coins in the box are 33.
1. Let's assume the number of 20-cent coins to be x and the number of 50-cent coins to be y.
2. We can set up two equations based on the given information:
- x + y = 54 (since the total number of coins in the box is 54)
- 0.20x + 0.50y = 20.70 (since the total value of all the coins is $20.70)
3. We can multiply the second equation by 100 to get rid of the decimals:
- 20x + 50y = 2070
4. Now, we can use the first equation to express y in terms of x:
- y = 54 - x
5. Substitute the value of y in the second equation:
- 20x + 50(54 - x) = 2070
6. Simplify and solve for x:
- 20x + 2700 - 50x = 2070
- -30x = -630
- x = 21
7. Substituting the value of x back into the first equation:
- 21 + y = 54
- y = 33
8. Therefore, there are 21 20-cent coins and 33 50-cent coins in the box.
For more such questions on Number, click on:
https://brainly.com/question/30752681
#SPJ8
Factories 6ax2-3ay-8bx2+4by
Answers
=[2\(x^{2}\)-y][3a-4b] This is the factorized form of 6a\(x^{2}\)-3ay - 8 b\(x^{2}\) + 4by
What is factorization ?To factorize a number, use the factorization formula. Factorization is the process of dividing a whole into components that, when multiplied together, equal the original number. The factorization approach simplifies any algebraic or quadratic equation by using the basic factorization formula, which represents the equations as the product of factors rather than expanding the brackets. Any equation may have an integer, a variable, or the algebraic expression itself as a factor.
6a\(x^{2}\)-3ay - 8 b\(x^{2}\) + 4by
Rearrange the expression
6a\(x^{2}\) -8bx² -3ay +4by
2\(x^{2}\)[3a-4b] - y[3a-4b]
=[2\(x^{2}\)-y][3a-4b]
This is the factorized form of 6a\(x^{2}\)-3ay - 8 b\(x^{2}\) + 4by
To learn more about factorization visit :
brainly.com/question/24182713
#SPJ10
90×4/9=40 is this equation true
Answers
The equation is correct, and the value on both sides of the equation is 40.
To verify if the equation 90 × 4/9 = 40 is true, we can perform the calculation on both sides and compare the results.
On the left side of the equation:
90 × 4/9 = (90 × 4) / 9 = 360 / 9 = 40
On the right side of the equation:
40
Both sides of the equation evaluate to 40, which means they are equal. Therefore, the equation 90 × 4/9 = 40 is indeed true.
In summary, the equation is correct, and the value on both sides of the equation is 40.
To learn more about equation :
https://brainly.com/question/17145398
#SPJ11
BRAINIEST TO WHOEVER CAN ANSWER THIS QUESTION!

Answers
Answer:B
Step-by-step explanation:
Step-by-step explanation:
This is a circle with center, h,k = 3,2 and radius = 2
circle equation is ( x-h)^2 + (y-k)^2 = r^2
so:
(x-3)^2 + (y-2)^2 = 4
Help me please I will mark as brainliest!!

Answers
Answer:
A is answer
Step-by-step explanation:
Cuz once you solve it isn't a fraction any more
I think