A ball is thrown vertically upward from the ground. Its distance in feet from the ground in t seconds is s equals negative 16 t squared plus 256 t. After how many seconds will the ball be 1008 feet from the​ ground?

Answer:

3/70

Step-by-step explanation:

Answer:

I think its 21/10

Step-by-step explanation:

because when you divide fractions you have to multiply.

Answer:

x = 31°

Step-by-step explanation:

the sum of the 3 angles in a triangle = 180° , that is

x + 54° + 95° = 180°

x + 149° = 180° ( subtract 149° from both sides )

x = 31°

Answer:

(C) Multiply first equation by -2 and second equation by 3, solution (1, 1)

Step-by-step explanation:

Simultaneous equations are set of equations which possess a common solution. The equations can be solved by eliminating one of the unknowns by multiplying each of the equations in a way that a common coefficient is obtained in the unknown to be eliminated.

Given the simultaneous equations:

3x - 5y = -2

2x + y = 3

First step:

Multiply first equation by -2 and multiply second equation by 3,

-6x + 10y = 4

6x + 3y = 9

Second step:

Add the two equations together,

13y = 13

Divide both sides by 13

y = 1

Third step:

Put y = 1 in the first equation

3x - 5(1) = -2

3x - 5 = -2

3x = 5 - 2

3x = 3

Divide both sides by 3:

x = 1

solution (x,y) = (1,1)

Option C

Learn more about simultaneous equations: https://brainly.com/question/30293776

#SPJ1

Answer:

2.50%

Step-by-step explanation:

To find the percentage of financial services companies that earned revenue greater than 35 million dollars, you need to use the standard normal distribution and the empirical rule. The empirical rule tells you that around 68% of values are within 1 standard deviation from the mean, around 95% of values are within 2 standard deviations from the mean, and around 99.7% of values are within 3 standard deviations from the mean.

First, you need to standardize the revenue value of 35 million dollars by converting it into a z score. A z score tells you how many standard deviations away from the mean a value is. The formula for z score is:

z = (x - M) / SD

where x is the value, M is the mean, and SD is the standard deviation.

Plugging in the given values, we get:

z = (35 - 80) / 22

z = -2.05

This means that 35 million dollars is 2.05 standard deviations below the mean.

Next, you need to use the empirical rule to find the percentage of values below this z score. Since 95% of values are within 2 standard deviations from the mean, and 35 million dollars is slightly more than 2 standard deviations below the mean, we can estimate that around 97.5% of values are below this z score. This means that only around 2.5% of values are above this z score.

Therefore, the percentage of financial services companies that earned revenue greater than 35 million dollars is approximately 2.5%. You can round this answer to the nearest hundredth and get 2.50%.

Answer: I believe it’s 10 ft

Step-by-step explanation:

Answer:

c

Step-by-step explanation:

The total area of the three triangles is square units is 36 and the area of the figure is square units is 60.

The triangle can be defined as a three-sided polygon in geometry, and it consists of three vertices and three edges. The sum of all the angles inside the triangle is 180°.

From the figure, the area of triangles can be calculated using the:

Area = (1/2)height×base length

Area of three triangle = 1/2(4×6) + 1/2(6×4) + 1/2(4×6)

Area of three triangle = 1/2(24×3) = 36 square units

Area of the figure = area of three triangle + area of the rectangle

= 36 + 6×4

= 60 square units

Thus, the total area of the three triangles is square units is 36 and the area of the figure is square units is 60.

Learn more about the triangle here:

brainly.com/question/25813512

#SPJ1

Answer:

The equation of the line is;

Explanation:

Given that the line is perpendicular to the equation;

So, the slope of the line will be the negative inverse of the slope of the equation above;

Also, the line passes through the point;

Applying the point-slope form of linear equation;

Substituting the values of the slope and coordinates;

Therefore, the equation of the line is;

Answer:

\(\frac{1}{32} yards^{3}\)

Step-by-step explanation:

\(V=w*h*l\)

↓

\(V= \frac{1}{4} *\frac{1}{4} *\frac{1}{2}\)

=

\(\frac{1}{32} yards^{3}\\\)

Hope this helps!

Answer:

Gina has 5 large shipping boxes and 6 small shipping boxes.

Step-by-step explanation:

32 items to ship and 11 shipping boxes.

Large=4 items

4 X 5 = 20

Small=2 items

2 X 6 = 12

20 + 12 = 32

Answer:

1.3 m²

Step-by-step explanation:

The shape is a trapezoid.

Area of a trapezoid = ½(a + b)*h

Where, a = 0.8 m

b = 1.8 m

h = height of the trapezoid which is not given.

Therefore, find h using trigonometric function with 45° as reference angle:

Hypotenuse = 1.4 m

Opposite = h

Apply SOH, which is:

Sin 45 = Opp/Hyp

Sin 45 = h/1.4

1.4*Sin 45 = h

0.989949493 = h

h ≈ 1.0 m

✔️Area of Trapezoid = ½(0.8 + 1.8)*1 = 1.3 m²

The solutions to the equation sin(θ) = √2/2 over the interval [0, 2π) are θ = π/4 and θ = 3π/4.

What is the trigonometric ratio?

the trigonometric functions are real functions that relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in all sciences that are related to geometry, such as navigation, solid mechanics, celestial mechanics, geodesy, and many others.

We know that sin(θ) = √2/2 is one of the standard angles in trigonometry, and it corresponds to an angle of 45 degrees or π/4 radians.

To solve the equation sin(θ) = √2/2 over the interval [0, 2π), we need to find all values of θ that satisfy the equation within this interval.

Since sin(θ) is positive in the first and second quadrants of the unit circle, we know that the solutions lie in those quadrants.

The first solution is θ = π/4, which corresponds to the angle of 45 degrees or π/4 radians in the first quadrant.

The second solution is θ = 3π/4, which corresponds to the angle of 135 degrees or 3π/4 radians in the second quadrant.

Therefore, the solutions to the equation sin(θ) = √2/2 over the interval [0, 2π) are θ = π/4 and θ = 3π/4.

To learn more about the trigonometric ratio visit:

https://brainly.com/question/13729598

#SPJ1

Answer:

The quadratic equation is in the standard form: ax^2 + bx + c = 0. To use the quadratic formula to find the solutions, we need to identify the values of a, b, and c in the equation:

a is the coefficient of the x^2 term, which is -3 in this case.

b is the coefficient of the x term, which is -5 in this case.

c is the constant term, which is 9 in this case.

Therefore, the values of a, b, and c in the quadratic equation -3x^2 - 5x + 9 = 0 are:

a = -3

b = -5

c = 9

Answer:

112 ounces

Step-by-step explanation:

Clay weighs 9 times as much as his baby sister .

Clay weighs 63 pounds.

His baby sister weigh 63/9.

His baby sister weighs 7 pounds.

But to be converted to ounce.

1 pound = 16 ounces

7 pounds = 7*16 ounces

7 pounds = 112 ounces

The function is given as.

f(x)={(8,3),(4,1),(0,-1),(-4,-3) }​

The inverse function is determined as a function, which can reverse into another function.

Therefore the inverse function g(x) is obtained as

Hence the correct option is D.

Answer:

i hate math

Step-by-step explanation:

Answer:

Zero solutions.

Step-by-step explanation:

4x - 8 - 4x = 9

-8 = 9

No solutions.

Answer:

Zero

Step-by-step explanation:

because:

4x - 8 -4x = 9

combine like terms:

4x - 4x = 0x

then look at the equation:

-8 = 9

this is not true. therefore, it has no solutions.

Hope this helped!!

The true statements are

The value of f(–10) = 82

The graph of the function is a parabola.

The graph contains the point (20, –8).

A parabola is a type of conic section that is formed when a plane intersects a cone in such a way that the angle between the plane and the vertical axis of the cone is equal to the angle between the plane and a generator (a straight line passing through the vertex and the base of the cone).

The resulting shape is a symmetrical, U-shaped curve. The standard form of the parabola is a quadratic function.

Here we have

The quadratic function f(x) = x²/5 – 5x + 12

Now check each option as follows

1. The value of f(–10) = 82

To check this find f(-10) as follows

f(-10) =1/5 (-10)²– 5(-10) + 12 = 20 + 50 + 12 = 82

Hence, The value of f(–10) is equal to  82

2. The graph of the function is a parabola.

As we know the standard equation of a parabola is a quadratic function that is in the form of ax² + bx + c

Hence, the quadratic function represents a parabola

3. The graph of the function opens down.

In the given function f(x) = x²– 5x + 12, the coefficient of the x² term is 1. Since the coefficient of x² is positive, the parabola opens upwards.

Hence, The graph of the function opens down is false

4. The graph contains the point (20, –8).

To check this substitute the point in f(x)

=> –8 = 1/5(20)²– 5(20) + 12

=> –8 = 80 – 100 + 12

=> –8 = –8   [ Which is true ]

Hence, The graph contains the point (20, –8).

5. The graph contains the point (0, 0).

=>  0 = (0)²– 5(0) + 12

=>  0 = 12   [ which is not true ]

Hence, The graph doesn't contain the point (0, 0).

Therefore,

The true statements are

The value of f(–10) = 82

The graph of the function is a parabola.

The graph contains the point (20, –8).

Learn more about Parabola at

https://brainly.com/question/21685473

#SPJ9

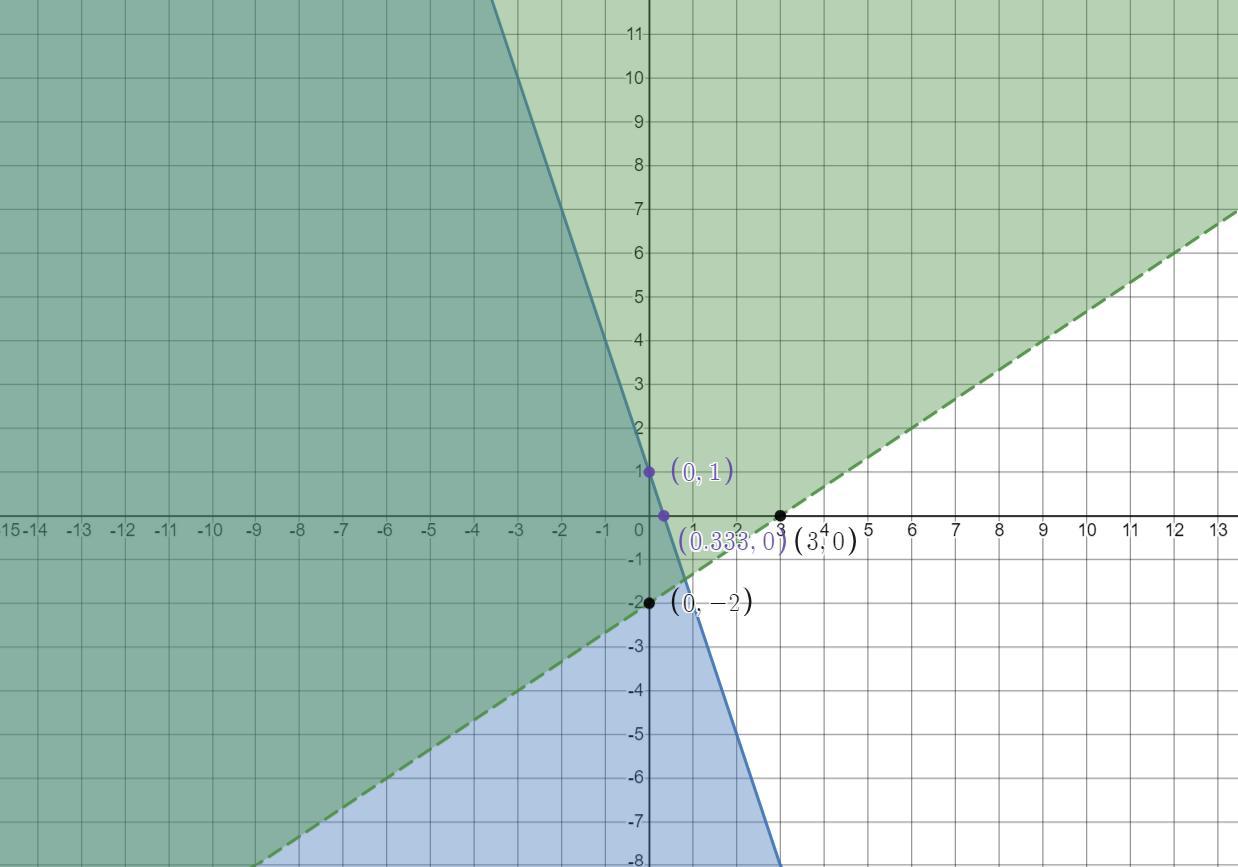
Given the System of Inequalities:

You can identify that the boundary lines are:

By definition, the Slope-Intercept Form of the equation of a line is:

Where "m" is the slope of the line and "b" is the y-intercept.

In this case, you can identify that the y-intercept of the first line is:

And the y-intercept of the second line is:

In order to find the x-intercept, you can substitute this value of "y" into each equation and solve for "x" (because the value of "y" is zero when the line intersects the x-axis):

Then, for the first line, you get:

And for the second line:

Now you know that the first line passes through these points:

And the second line passes through these points:

Notice that the symbol of the first inequality is:

That indicates the boundary line is solid and the shaded region is below the line.

The symbol of the second inequality is:

It indicates that is the boundary line is dashed and the shaded region is above the line.

The solution region is the intersection region between the inequalities.

Knowing the above, you can graph the System of inequalities.

Hence, the answer is:

Answer:

9 pigs

Step-by-step explanation:

If 4 of them didn't die, he'd have made 8 more dollars. 18/2=9.

The total weight of all the cantaloupes that weigh more than 2 1 / 2 pounds is 8 2 / 4 lb ​.

As shown on the line plot, the number of cantaloupes with a higher mass than 2 1 / 2 pounds are those which have a weight of 2 3 / 4 pounds.

There are enough of them that when they are added up, we get the sum of 8 2 / 4 lb​ as the total mass of the cantaloupes. This can also be written in decimals as 8. 5 lb.

In conclusion, option D. is correct.

Find out more on weight at https://brainly.com/question/18802926

#SPJ1

The correct answer is 3/2. In this case, x = 3/2, and its square, (3/2)^2 = 9/4, is rational. x satisfies the given condition.option (c)

To explain further, we need to understand the properties of rational and irrational numbers.

A rational number can be expressed as a fraction of two integers, while an irrational number cannot be expressed as a fraction and has non-repeating, non-terminating decimal representations.

In the given options, (a) √5102.0 (£) and (b) √2 are both irrational numbers.

Their squares, (√5102.0)^2 and (√2)^2, would also be irrational, violating the given condition. On the other hand, (d) 4/5 is rational, and its square, (4/5)^2 = 16/25, is also rational.

Option (c) 3/2 is rational since it can be expressed as a fraction. Its square, (3/2)^2 = 9/4, is rational as well.

Therefore, (c) 3/2 is the only option where x is rational, but its square is irrational, satisfying the condition mentioned in the question.

In summary, the number x that satisfies the given condition, where x^2 is irrational but x is rational, is (c) 3/2.option (c)

for such more questions on rational

https://brainly.com/question/30339525

#SPJ8

A: The reasonable domain to plot the growth function would be all positive integers for the number of days, d, since the growth occurs over time.

B: The y-intercept of the graph of the function f(d) represents the initial radius of the algae when d = 0. In this case, the y-intercept is 9 mm.

C: To find the average rate of change of the function from d = 3 to d = 9, we need to find the difference in the radius of the algae at d = 9 and d = 3 and divide by the difference in the number of days.

f(9) = 9(1.04)^9 = 12.81 mm

f(3) = 9(1.04)^3 = 10.46 mm

Average rate of change = (12.81 - 10.46) / (9 - 3) = 0.71 mm/day

The average rate of change represents the average amount by which the radius of the algae increases each day from d = 3 to d = 9.

Answer

its scale factor is ​4/3 and 0.75

Step-by-step explanation:

The time taken to reaches its maximum height is 3s.

In the question,

It is given that,

Height, h(t) = \(96t - 16t^{2}\)

The maximum value of the function is obtained if the first derivative of the function h (t) = 0.

\(\frac{dh(t)}{dt} = 96 - 32t = 0\)

⇒ \(t = 3\)

So, time taken to reach its max height is 3 seconds.

Learn about max height here

https://brainly.com/question/12298041

#SPJ1

Answer:

0.592

Step-by-step explanation:

Total Number of Students =125

Out of these, 74 reported that they have completed their required English 101 course.

To find the best point estimate for the proportion of students at the college who have completed their required English 101 course, we divide the number of students who said "yes" by the total number of students.

\(\text{Point Estimate }=\dfrac{74}{125} \\=0.592\)

Answer:

180 people

Step-by-step explanation:

Total of people surveyed = 1,000

% of people that selected travelling as their favorite hobby = 18 %

Number of people that selected travelling = % that selected travelling of 1,000

= 18% of 1,000

= 18/100 × 1,000

= 180 people

Therefore, 180 people selected travelling as their favorite hobby.

Answer:

error in Step 2

Step-by-step explanation:

2(x - 3) + 3x = 19

Step 1 : 2x - 6 + 3x = 19 ← simplify left side by collecting like terms

Step 2 : 5x - 6 = 19 ← add 6 to both sides

Step 3 : 5x - 6 + 6 = 19 + 6

Step 4 : 5x = 25 ← divide both sides by 5

Step 5 : x = 5

Error was made by student in Step 2 who should have added 2x and 3x, not multiplied 2 × 3

Answer: y= 2x - 5

Step-by-step explanation: lmk if u need explanation to solve

Answer: 23100 voters

Step-by-step explanation:

42*55000=2310000

2310000/100=23100 voters