80 – 2 x (3 + 2)Squared
Answers
Answer:
80-50x
Step-by-step explanation:
Answer:
30
.... just use a calculator
Related Questions
2 + (8 - 4) + 32 * 3
Answers
Answer: 102
Step-by-step explanation:
solved
helpppppp i need help with this rn

Answers
Subtract 83 from both sides 4t-7=97 then add 7 on each side 4t=104 then divide each side by 4 t=26 then plug 26 in for t and get your answer which should equal 97 then just add the other angle which was 83 and you will get 180
Jill can run 5 miles in 45 minutes. If she keeps the same pace, how long will it take her to run 18 miles?
Answers
Answer:
T = 162 minutes
Step-by-step explanation:
Given that,
Jill can run 5 miles in 45 minutes.
We need to find how long will it take her to run 18 miles.
\(5\ miles =45\ minutes\\\\1\ mile=(\dfrac{45}{5})\ minute\\\\1\ mile =9\ minute\)
So,
18 miles = (18×9) minutes
= 162 minutes
Hence, 162 minutes will be taken by her to run 162 minutes.
Leily was guessing Joseph’s number. He said that his number was composite, even, and a square number between 15 and 30. What is Joseph’s number?
Answers
The number that Joseph is thinking of that is between 15 and 30 is 16.
What is Joseph’s number?The first step is to determine the squares between 15 and 30. The square of a number is the product of a number with itself. For example, 16 is a square number.
Squares between 15 and 30 = 16, 25
The next step is to determine the even number. An even number is a number that is perfectly divisible by 2. An example of an even number is 4.
The even number that is a square between 15 and 30 is 16.
The last step is to determine the composite number. A composite number is a number that has more than 2 factors.
Factors of 16 = 1, 2, 4, 8, 16
To learn more about even numbers, please check: https://brainly.com/question/2289438
#SPJ1
the p-value is the probability that the null hypothesis is true.
t
f
Answers
The statement "the p-value is the probability that the null hypothesis is true" is not accurate.
The p-value is a statistical measure that is used to determine the strength of evidence against the null hypothesis. It represents the probability of observing the data or more extreme data, assuming that the null hypothesis is true.
To understand this concept better, let's break it down into steps:
1. Null hypothesis: In hypothesis testing, we start with a null hypothesis, which is a statement that assumes there is no significant difference or relationship between variables. For example, in a study comparing the effectiveness of two drugs, the null hypothesis would state that there is no difference in effectiveness.
2. Alternative hypothesis: Alongside the null hypothesis, we also have an alternative hypothesis, which states that there is a significant difference or relationship between variables. Using the previous example, the alternative hypothesis would suggest that there is a difference in effectiveness between the two drugs.
3. Test statistic: After defining the null and alternative hypotheses, we calculate a test statistic using the available data. The test statistic varies depending on the type of hypothesis test being conducted.
4. P-value interpretation: The p-value represents the probability of obtaining the observed data, or more extreme data, assuming that the null hypothesis is true. If the p-value is small (typically below a predetermined threshold, such as 0.05), it suggests that the observed data is unlikely to occur by chance alone if the null hypothesis is true. In this case, we reject the null hypothesis and provide support for the alternative hypothesis.
5. Conclusion: Based on the p-value and predetermined significance level, we make a conclusion regarding the null hypothesis. If the p-value is less than the significance level, we reject the null hypothesis in favor of the alternative hypothesis. If the p-value is greater than the significance level, we fail to reject the null hypothesis.
In summary, the p-value is not the probability that the null hypothesis is true. Instead, it represents the probability of obtaining the observed data or more extreme data, assuming the null hypothesis is true. By comparing the p-value to a predetermined significance level, we can make conclusions about the null hypothesis and provide evidence for the alternative hypothesis.
Know more about null hypothesis here:
https://brainly.com/question/28920252
#SPJ11
g/7-5=1 1/2 what deos g equals
Answers
Answer:
g = 45.5
Step-by-step explanation:
45.5 ÷ 7 = 6.5
6.5 - 5 = 1.5
Answer:
45 1/2
Step-by-step explanation:
45.5 / 7 = 6.5 - 5 = 1.5 or 1 1/2
Which of the following is correct equation for the trend line in the scatter plot? A. Y= 2/5 x -2 B. Y= 5x-1 C. Y= 5x +5 D. Y= -x+5

Answers
The equation for the trend line in the scatter plot will be Y= 5x-1. Option B is correct.
What is a scatter plot?In an effort to demonstrate how much one variable is influenced by another, scatter plots are used to depict data points on a horizontal and vertical axis.
When there is no connection between two variables, it is called a zero correlation. For instance, there is no correlation between IQ level and the quantity of tea consumed.
The graphs are attached in the attachment.
The equation for the trend line in the scatter plot will be Y= 5x-1.
Hence, option B is correct.
To learn more about the scatterplot refer to:
https://brainly.com/question/13984412#SPJ1
#SPJ1


somebody pls helpp meee

Answers
Answer:
1 and 3
Step-by-step explanation:
+ 3 & 1 belong to the solution
Whats the distance between -6 and 2
Answers
Answer:
4
Step-by-step explanation:
if you take -6 and subtract it by 2 it equals -4
A salesperson receives 12% commission on all the sales that she makes. Calculate the
commission on each sale.
a. A quarter page ad for $250.00
b. A full page ad for $800.00
Answers
b) 800.00 x 0.12 = $96
(Competing patterns among coin flips) Suppose that Xn, n 2 1 are i.i.d. random variables with P(X1 = 1) = P(X1 = 0) = }. (These are just i.i.d. fair coin flips.) Let A = (a1, a2, a3) = (0,1, 1), B = (b1, b2, b3) = (0,0, 1). Let TA = min(n 2 3: {X,-2, Xn-1, Xn) = A} be the first time we see the sequence A appear among the X, random variables, and define Tg similarly for B. Find the probability that P(TA < TB). (This is the probability that THH shows up before TTH in a sequence of fair coin flips.)
Answers
The probability of A appearing before B is \(\frac{4}{7}\).
To find the probability that TA < TB, we can use the fact that the probability of a certain pattern appearing in a sequence of coin flips is independent of the position in the sequence. In other words, the probability of A appearing at time n is the same as the probability of A appearing at time n+k for any k.
Using this fact, we can set up a system of equations to solve for the probability of TA < TB. Let p be the probability of A appearing before B, and q be the probability of B appearing before A. Then we have:
\(p = \frac{1}{2} + \frac{1}{2q}\) (since the first flip can be either 0 or 1 with equal probability)
\(q= \frac{1}{4p} + \frac{1}{2q} + \frac{1}{4}\) (if the first two flips are 0, the sequence B has appeared; if the first flip is 1 and the second is 0, the sequence is neither A nor B and we start over; if the first flip is 1 and the second is 1, we have a new chance for A to appear before B)
Solving for p, we get:
\(p=\frac{4}{7}\)
Therefore, the probability of A appearing before B is \(\frac{4}{7}\).
To know more about "Probability" refer here:
https://brainly.com/question/30034780#
#SPJ11
Please help me solve this guys

Answers
Answer:
Factored Form: y=(x+1) ( x+3)y=(x+1)(x+3)
X-intercepts: (-1,0), (-3,0)(−1,0),(−3,0)
Axis of Symmetry: x= -2x=−2
Vertex: (-2,-1)(−2,−1)
Domain: (\begin{gathered}(-\infty , \infty ), ( x | x ER)\\\end{gathered}
(−∞,∞),(x∣xER)
Range: y > =-1y>=−1
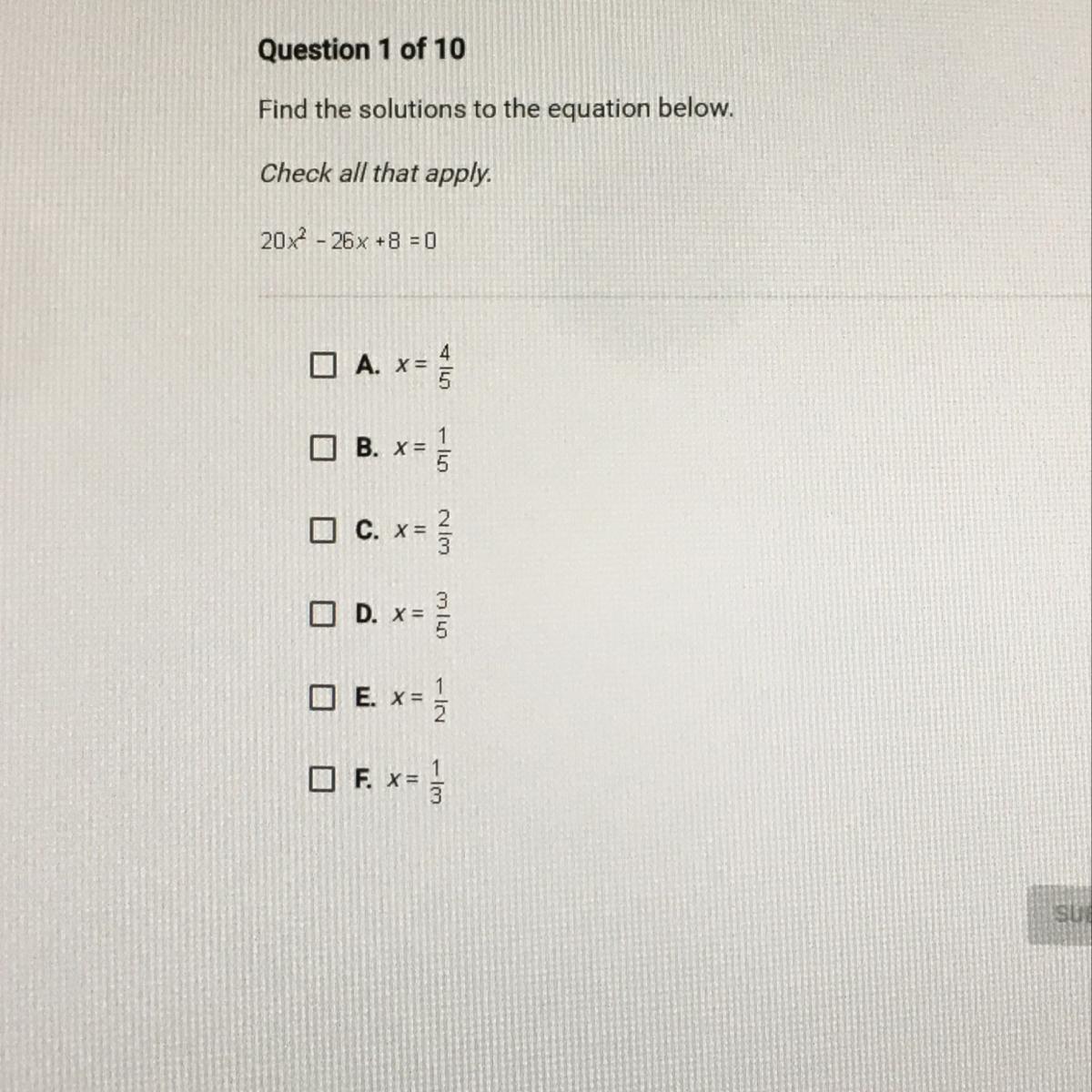
find the solutions to the equation below. 20x^2 - 26x + 8 = 0
Check all that apply.
A. x = 4/5
B. x = 1/5
C. x = 2/3
D. x = 3/5
E. x = 1/2
F. x = 1/4
Answers
To aid in sea navigation, Little Gull Island Lighthouse shines a light from a height of 91 feet above sea level with an unknown angle of depression. If the beam of light shines on the sea surface at a point that is 865 feet away from the base of the lighthouse, what is the angle of depression?
Answers
Answer:
\(\approx 6^\circ\)
Step-by-step explanation:
Given that:
Little Gull Island Lighthouse shines a light from a height of 91 feet above the sea level.
The angle of depression is unknown.
Distance of the point at sea surface from the base of lighthouse is 865 ft.
This situation can be modeled or can be represented as the figure attached in the answer area.
The situation can be represented by a right angled \(\triangle ABC\) in which we are given the base and the height of the triangle.
And we have to find the value of \(\angle BAD \ or \ \angle C\) (Because they are the internal vertically opposite angles).
Using tangent ratio:
\(tan\theta = \dfrac{Perpendicular}{Base}\)
\(tanC = \dfrac{AC}{BC}\\\Rightarrow tanC = \dfrac{91}{865}\\\Rightarrow tanC = 0.105\\\Rightarrow \angle C \approx 6^\circ\)
Therefore, the angle of depression is: \(\approx 6^\circ\)

A hockey player made 9 goals in 12 games. find the ratio of goals to games. a. 3:4 c. 1:3 b. 4:3 d. 3:1
Answers
==========================================================
Reason:
There are 9 goals in 12 games, which produces the ratio 9:12. The order of the values is important since we list the goals first (because we have "goals" before "games" mentioned).
After setting up 9:12, we divide both parts by the GCF 3
9/3 = 3
12/3 = 4
The ratio 9:12 fully reduces to 3:4 as the final answer
Find z so that 88% of the area is to the right of z.
Answers
• We are required to find Z so that the area is to the right, this means that the area is to be positive .
,• 88 % can be converted to 88/100 = 0.88
,• z = 1-0.88 = 0.12
The value tha corresponds with 0.12 = 0.04775
= 0.048
using the cumulative standard normal z score of 0.12 = 0.5478
write an equation for the horizontal line that passes through
Answers
the equation of the horizontal line passing through (-3, 4) is y = 4.
The equation of a horizontal line is of the form y = c, where c represents the y-coordinate of any point on the line. In this case, we are given that the line passes through the point (-3, 4). Since the line is horizontal, the y-coordinate remains constant for all points on the line.
Therefore, the equation of the horizontal line passing through (-3, 4) is y = 4. This means that no matter what x-value we choose, the y-value will always be 4.
In other words, all the points on this line will have a y-coordinate of 4.
Learn more about Horizontal line here
https://brainly.com/question/14183046
#SPJ4
Complete question is below
Write the equation of the horizontal line that passes through (-3, 4).
The equation for the horizontal line that passes through a given point is y = b.
A horizontal line is a straight line that is parallel to the x-axis. The equation of a horizontal line is of the form y = c, where c is a constant. Since the line is horizontal, the value of y remains constant for all values of x. Therefore, the equation of a horizontal line passing through a given point (a, b) is y = b.
Learn more:About equation here:
https://brainly.com/question/29538993
#SPJ11
Which method would be appropriate to factor the polynomial below. 55x^3-40x^2 -Difference of Squares -Basic Trinomial Factoring -AC Method -Sums of Cubes -Greatest Common Factor -Factors by grouping
Answers
Answer:
Greatest Common Factor
Step-by-step explanation:
Let \(55\cdot x^{3}-40\cdot x^{2}\), we proceed to demonstrate the appropriate form to factor the polynomial:
1) \(55\cdot x^{3}-40\cdot x^{2}\) Given.
2) \((5\cdot 11)\cdot (x^2\cdot x) +[5\cdot (-8)]\cdot x^{2}\) Definition of multiplication and subtraction/\(a^{b+c} = a^{b}\cdot a^{c }\)/\(-a\cdot b = (-a)\cdot b\)/Associative property
3) \((5\cdot x^{2})\cdot (11\cdot x)+ (5\cdot x^{2})\cdot (-8)\) Commutative and associative properties
4) \(5\cdot x^{2}\cdot (11\cdot x-8)\) Distributive property/Definition of subtraction/Result
Hence, we conclude that this polynomial can be factored by Greatest Common Factor.
This is part one of the problem posting part two after this

Answers
Answer:
new image should be 4 x 8
post the pictures for the questions
Step-by-step explanation:
If my answer is incorrect, pls correct me!
If you like my answer and explanation, mark me as brainliest!
-Chetan K
Write the equation of the quadratic function whose graph passes through \((-3,2)\), \((-1,0)\), and \((1,6)\).
Answers
Answer:
\(f(x)=x^2+3x+2\)
Step-by-step explanation:
We want to write the equation of a quadratic whose graph passes through (-3, 2), (-1, 0), and (1, 6).
Remember that the standard quadratic function is given by:
\(f(x)=ax^2+bx+c\)
Since it passes through the point (-3, 2). This means that when \(x=-3\), \(f(x)=f(-3)=2\). Hence:
\(f(-3)=2=a(-3)^2+b(-3)+c\)
Simplify:
\(2=9a-3b+c\)
Perform the same computations for the coordinates (-1, 0) and (1, 6). Therefore:
\(0=a(-1)^2+b(-1)+c \\ \\0=a-b+c\)
And for (1, 6):
\(6=a(1)^2+b(1)+c\\\\ 6=a+b+c\)
So, we have a triple system of equations:
\(\left\{ \begin{array}{ll} 2=9a-3b+c &\\ 0=a-b+c \\6=a+b+c \end{array} \right.\)
We can solve this using elimination.
Notice that the b term in Equation 2 and 3 are opposites. Hence, let's add them together. This yields:
\((0+6)=(a+a)+(-b+b)+(c+c)\)
Compute:
\(6=2a+2c\)
Let's divide both sides by 2:
\(3=a+c\)
Now, let's eliminate b again but we will use Equation 1 and 2.
Notice that if we multiply Equation 2 by -3, then the b terms will be opposites. So:
\(-3(0)=-3(a-b+c)\)
Multiply:
\(0=-3a+3b-3c\)
Add this to Equation 1:
\((0+2)=(9a-3a)+(-3b+3b)+(c-3c)\)
Compute:
\(2=6a-2c\)
Again, we can divide both sides by 2:
\(1=3a-c\)
So, we know have two equations with only two variables:
\(3=a+c\text{ and } 1=3a-c\)
We can solve for a using elimination since the c term are opposites of each other. Add the two equations together:
\((3+1)=(a+3a)+(c-c)\)
Compute:
\(4=4a\)
Solve for a:
\(a=1\)
So, the value of a is 1.
Using either of the two equations, we can now find c. Let's use the first one. Hence:
\(3=a+c\)
Substitute 1 for a and solve for c:
\(\begin{aligned} c+(1)&=3 \\c&=2 \end{aligned}\)
So, the value of c is 2.
Finally, using any of the three original equations, solve for b:
We can use Equation 3. Hence:
\(6=a+b+c\)
Substitute in known values and solve for b:
\(6=(1)+b+(2)\\\\6=3+b\\\\b=3\)
Therefore, a=1, b=3, and c=2.
Hence, our quadratic function is:
\(f(x)=x^2+3x+2\)
Name:
Quadrilateral ABCD is a rectangle.
A
B
I
D
5. If AG = -48 +24 and DG =9k + 102, find BD.
A. 96
B. -6
D. 48

Answers
Answer:
As AG = DG
so -4k +24 = 9k + 102
=> -4k - 9k = 102-24
=> -13k = 78
=> k = -6
So the length of DG = -4k + 24 = 24 + 24 = 48
As BG+DG = 2DG = 2(48) = 96 (ans)
So no. c is correct
Hope it helps
1) d=rt
d = distance traveled by a moving object
r = rate of speed
time the object travels
t = time the object travels
Your first stop is in Bend, which is 122 miles away. How
fast do you need to travel in order to make it there in 3
hours?
Answers
Answer:
41 mph
Step-by-step explanation:
122 = 3r
r = 40 2/3 mph
Which of these will not help you achieve a goal?
help please

Answers
Answer:
Hello! Mizuki here to help. The correct option you choose should be the second one(hoping you meet it)
Just hoping and not trying to achieve the goal won't help. The others are important step(s) to achieve a goal.
Step-by-step explanation:
Find five solution for the linear equation 2x - y = 2, and complete the table below
Answers
Answer:
x-intercept(s):
(
1
,
0
)
y-intercept(s):
(
0
,
−
2
)
Step-by-step explanation:
I need help with these question not sure what I'm doing wrong

Answers
Answer:
7. 9.4%
8. 9.4ft
Step-by-step explanation:
Question 7:
The percent grade is another term for slope
The slope formula is rise over run
The rise in question 7 is 1500 meters
The run in question 7 is 16km, or 16000 meters
1500/16000 is 0.09375. 0.09375 in percent is 9.375%
round to the nearest tenth, and it is 9.4%
Question 8:
To solve this question you must know what the pythagorean theorem is.
The pythagorean theorem: in a right triangle the square of the hypotenuse is equal to the sum of the squares of the two legs.
Famously known as a^2+b^2 =c^2
The "length" of the rail would be the hypotenuse
(the rise and the run are the legs of the "triangle")
the rise in question 8 is 5 feet
the run in question 8 is 8 feet
5^2 + 8^2 = c^2
25+64=c^2
89=c^2
√89 = √c^2
c = 9.43398113...
round to the nearest tenth to get 9.4 ft
Which expression is equivalent to 27s+18t+45?
A. 9s(3 + 18t + 45)
B. 3(9s + 6t + 15)
C. 2(27s + 9t + 45)
Answers
Answer:
B
Step-by-step explanation:
yeah it's B welcome lllllllll
please graph y≤ 2x-3
Answers

Find the equation of the line with a slope of − 1/2 through (4, 5)
Answers
Answer: Hello:
Slope - intercept form is y = mx + b.
Since -1/2 is your slope and 5 is your y - intercept, all you need to do is substitute those values into the equation:
y = -1/2 + 5
Hope this helps!
2n+1=157 what is the first number
Answers
Find the distance between each pair of points.
1. 1-4.6) and (3.-7)
2. (-6,-5) and (2.0)
M=(-12,-1)
M=
4. (0.-8) and (3.2)
3. (-1, 4) and (1-1)
Answers
The distances between each pair of points are as follows:
1. (1, -4.6) and (3, -7): 3.12 (rounded to two decimal places)
2. (-6, -5) and (2, 0): √89 (exact value)
M = (-12, -1) and M = (4, 0): √257 (exact value)
4. (0, -8) and (3, 2): √109 (exact value)
3. (-1, 4) and (1, -1): √29 (exact value)
We may use the distance formula to calculate the separation between each pair of points:
d = √((x₂ - x₁)² + (y₂ - y₁)²),
where the two points' coordinates are represented by (x1, y1) and (x2, y2), respectively.
Let's determine the separation between each pair of points:
1. (1, -4.6) and (3, -7):
d = √((3 - 1)² + (-7 - (-4.6))²)
= √(2² + (-2.4)²)
= √(4 + 5.76)
= √9.76
= 3.12 (rounded to two decimal places)
2. (-6, -5) and (2, 0):
d = √((2 - (-6))² + (0 - (-5))²)
= √(8² + 5²)
= √(64 + 25)
= √89 (exact value)
M = (-12, -1) and M = (4, 0):
d = √((4 - (-12))² + (0 - (-1))²)
= √(16² + 1²)
= √(256 + 1)
= √257 (exact value)
4. (0, -8) and (3, 2):
d = √((3 - 0)² + (2 - (-8))²)
= √(3² + 10²)
= √(9 + 100)
= √109 (exact value)
3. (-1, 4) and (1, -1):
d = √((1 - (-1))² + (-1 - 4)²)
= √(2² + (-5)²)
= √(4 + 25)
= √29 (exact value)
For more such question on distances. visit :
https://brainly.com/question/30395212
#SPJ8