3x-4x-14=9
Solve please
Answers
Answer:
x = -23
Step-by-step explanation:
3x-4x-14=9
-x = 9 + 14
-x = 23
x = -23
Related Questions
WEEK 2 Direction: Answer the following problems. 1. Jun wanted to know how much ice cream he got in on scoop. The radius of a scoop is 2 inches. Find the volum Use 3.14 for pi. (SHOW YOUR SOLUTION) a) What is asked in the problem? b) What are the given facts? c) What is the formula to be used? d) Number Sentence e) Final answer. (show your solution pls)
Answers
We are given the radius of the scoop and asked to find the volume of ice cream in one scoop. By using the formula for the volume of a sphere and substituting the given radius, we can calculate the volume. The final answer is approximately 33.49 cubic inches.
a) The problem asks for the volume of ice cream in one scoop.
b) The given fact is that the radius of the scoop is 2 inches.
c) The formula to be used is the volume of a sphere, which is given by V = (4/3)πr³, where V is the volume and r is the radius.
d) Number Sentence:
- Given: Radius (r) = 2 inches
- Formula: V = (4/3)πr³
- Substituting the value: V = (4/3)π(2)³
- Simplifying: V = (4/3)π(8)
- Evaluating: V = (4/3)(3.14)(8)
- Multiplying: V = 33.49333333 (approx.)
e) Final answer: The volume of ice cream in one scoop is approximately 33.49 cubic inches.
For more such questions on volume
https://brainly.com/question/1972490
#SPJ8
The product of 4 and the difference of a number and 7.
Answers
Answer:
simplified: 4x−28
Step-by-step explanation:
The product of 4 and the difference of a number and 7 can be written as 4(x-7) where x is the number you are looking for.
Choose the best option.
1.(101), in base 10 is equal to:
a)10
b)1
c)2
d)5
Answers
Answer:5
Step-by-step explanation:(1×2^2)+(0×2^1)+(1×2^0)=
1×4+0×2+1×1=
4+1=
5
Which expression represents the phrase ""the product of x and the quantity ‘10 minus x’""?
Answers
nobody can answer this by their own part 4

Answers
Answer:
28 days
Step-by-step explanation:
Day 1 = 3 m, day 1 end = 3 - 1 = 2 m
Day 2 end = 2 + 3 -2 = 3m
Day3 end = 3 + 3- 2 = 3 +1 = 4m
On 27th day end = 26+ 3 - 2 = 27 m
On 28th day =27 + 3 = 30 m
every day amy travels 30 miles one-way to work. The park-and-ride where she catches the train is 5 miles from her home. The average speed of the train is 15 mph faster than the average speed in her car. assuming she has no wait time for the train, her one-way trip takes 45 minutes. Find the speed of the car.
Answers
Answer:
Speed= 0.6666667 miles per hour
Step-by-step explanation:
You can find the average speed of an object if you know the distance traveled and the time it took. The formula for speed is speed = distance ÷ time. To work out what the units are for speed, you need to know the units for distance and time.
5⁶ • 5 how do i simplify
Answers
Which of the binomials below is a factor of this trinomial? 4x2 + 12x + 9A. 2x-3B. 2x-1C. 2x+1D. 2x+3
Answers
In order to factorate the trinomial, let's first find its roots using the quadratic formula:
\(\begin{gathered} b^2-4ac=12^2-4\cdot4\cdot9=144-144=0 \\ x_1=x_2=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}=\frac{-12+0}{2\cdot4}=-\frac{12}{8}=-\frac{3}{2} \end{gathered}\)Now we can write the trinomial in the form:
\(a(x-x_1)(x-x_2)\)So we have that:
\(4x2+12x+9=4(x+\frac{3}{2})(x+\frac{3}{2})=(2x+3)(2x+3)\)So 2x + 3 is a factor of the trinomial, therefore the answer is D.
The temperature of a cup of coffee varies according to Newton's Law of Cooling: dT dt equals negative k times the quantity T minus A, where T is the temperature of the coffee, A is the room temperature, and k is a positive constant. If the coffee cools from 100°C to 90°C in 1 minute at a room temperature of 25°C, find the temperature, to the nearest degree Celsius of the coffee after 4 minutes.
74
67
60
42
Answers
Answer:
67
Step-by-step explanation:
A = 25, T(0) = 100, T(1) = 90, find T(4)
dT/dt = -k(T - A)
d(T - A)/dt = -k(T - A)
d(T - A)/(T - A) = -k dt
ln(T - A) = lnC - kt
\(T(t) -A=Ce^{-kt}\\T(t) = A + Ce^{-kt} = 25 + Ce^{-kt}\\T(0) = 25 + C = 100\\C=75\)
\(T(t) = 25 + 75e^{-kt}\\T(1) = 25 + 75e^{-k} = 90\\75e^{-k} = 65\\e^{-k} = \frac{65}{75}, k = ln\frac{75}{65} = 0.1431\\T(t) = 25+75e^{-0.1431t}\\T(4) = 25+75e^{-0.1431\times4} = 67.3\)
Find the 75th term of the following arithmetic sequence 16,25,34,43
Answers
Answer:
\(\boxed {\boxed {\sf 682}}\)
Step-by-step explanation:
The nth term of an arithmetic sequence can be found using the following formula.
\(a_n=a+d(n-1)\)
where a is the first term, d is the common difference, and n is the term.
First, we should find the common difference.
We can do this by subtracting each term from the term following it. Basically, subtract the first term from the second term, the second from the third, and so on.
\(d= a_2-a_1\)
The second term is 25 and the first is 16.
\(d= 25-16\)
\(d=9\)
Now we know the common difference is 9. We also know the first term is 16 and we are looking for the 75th term.
\(d=9 \\a=16 \\n= 75\)
Substitute the values into the formula.
\(a_{75}=16+9(75-1)\)
Solve according the PEMDAS (Parentheses, Exponents, Multiplication, Division, Addition, Subtraction).
Solve the parentheses first.
\(a_{75}=16+9(74)\)
Multiply next.
\(a_{75}=16+666\)
Finally, add.
\(a_{75}=682\)
The 75th term in the sequence is 682.
Uri paid a landscaping company to mow his lawn. The company charged $74 for the service plus
5% tax. After tax, Uri also included a 10% tip with his payment. How much did he pay in all?
Answers
Uri paid a total of $85.47 for the landscaping service including tax and tip.
What is tax?Taxes are compulsory payments made by a government organisation, whether local, regional, or federal, to people or businesses. Tax revenues are used to fund a variety of government initiatives, such as Social Security and Medicare as well as public infrastructure and services like roads and schools. Taxes are borne by whoever bears the cost of the tax in economics, whether this is the entity being taxed, such as a business, or the final users of the items produced by the firm. Taxes should be taken into consideration from an accounting standpoint, including payroll taxes, federal and state income taxes, and sales taxes.
Given that company charged $74 for the service plus 5% tax.
The tax is 5%, that is:
Tax = 5% of $74 = 0.05 x $74 = $3.70
Cost after tax = $74 + $3.70 = $77.70
Now, tip is 10%:
Tip = 10% of $77.70 = 0.10 x $77.70 = $7.77
Total cost = $77.70 + $7.77 = $85.47
Hence, Uri paid a total of $85.47 for the landscaping service including tax and tip.
Learn more about tax here:
https://brainly.com/question/16423331
#SPJ1
A figure is shown, where lines CE and FD intersect at point B.
.
A figure is shown, where lines CE and FD intersect at point B.
.
Angle ABC is complementary to angle DBC.
What is the measure, in degrees of ?
Answers
Answer:
Step-by-step explanation:
Its 4.51
Find the value of x and y in simplified radical form.

Answers
x and y have the values 7 and 7√2, respectively.
The sides of a right triangle with 45-degree acute angles have a unique ratio of 1:1:2.
We can use this information to determine the values of x and y because the base is specified as being 7.
Let's give the perpendicular side the value of x, and the hypotenuse the value of y.
The perpendicular side (x) and the base (7) have the same length because the acute angles are both 45 degrees.
Consequently, x = 7.
We can determine that x:y:2x using the ratio of 1:1:2.
When we enter the value of x, we may calculate y:
7:y:√2(7)
Simplifying even more
7:y:7√2
Given that the hypotenuse (y) equals 72, we can write:
y = 7√2
Thus, x and y have the values 7 and 7√2, respectively.
Learn more about right triangle click;
https://brainly.com/question/30966657
#SPJ1
1. In a class of 60 students, a survey was conducted, 30 students had applied for Addis Ababa University, 25 students applied for Bahir Dar University and 24 students applied for Wachemo University. 11 students applied for both Addis Ababa and Bahir Dar Universities, 6 applied for both Addis Ababa and Wachemo Universities, 9 applied for both Wachemo and Bahir Dar Universities while 4 applied neither of the aforementioned universities. Find 1.. number of students that applied for all the universities. 2 number of students that applied for at least two of the universities. 3 number of students that applied at most two universities. 4 number of students that applied for Addis Ababa but not Bahir Dar University? Please I need your help?
Answers
1. Consult the linked question. \(n(A\cap B\cap W) = \boxed{3}\).
2. We have
\(n(A\cap B) = n(A\cap B \cap W) + n(A\cap B \cap W') \\\\ \implies 11 = 3 + n(A\cap B \cap W') \\\\ \implies n(A\cap B\cap W') = 8\)
Similarly we can find
\(n(A\cap B' \cap W) = 3\)
\(n(A'\cap B\cap W) = 6\)
\(n(A\cap B'\cap W') = 16\)
\(n(A'\cap B\cap W') = 8\)
\(n(A'\cap B'\cap W) = 12\)
Then the total number of students that applied to at least two of the universities is
\(\underbrace{n(A\cap B\cap W') + n(A\cap B'\cap W) + n(A'\cap B\cap W)}_{\text{only 2}} + \underbrace{n(A\cap B\cap W)}_{\text{all 3}} = \boxed{20}\)
3. There's a small ambiguity here. Are we interested in students that applied to zero universities? If so, there are
\(\underbrace{n(U\setminus(A\cup B\cup W))}_{\text{none}} + \underbrace{n(A\cap B'\cap W') + n(A'\cap B\cap W') + n(A'\cap B'\cap W)}_{\text{only 1}} = \boxed{40}\)
If we want students that applied to at least 1 school, we omit the first term and get a total of 36.
4. Split this set of students into those that also applied to Wachemo and those that did not.
\(n(A \cap B') = n(A\cap B' \cap W) + n(A\cap B'\cap W') = \boxed{19}\)

what is the percent of decrease from 100 to 49
Answers
A boy runs a distance of 200km in 25seconds. What is his average speed
Answers
Answer:
8 km average speed
Step-by-step explanation:
Answer:
His average speed is 28,800 km per hour.
Step-by-step explanation:
He runs 480 km per minute. Then I multiply 480 by 60 to get 28,800 km.
:))
What is the meaning of "\( \varphi (x,y)\) be \( y\wedge \phi (x)\) "?
![What is the meaning of "[tex] \varphi (x,y)[/tex] be [tex] y\wedge \phi (x)[/tex] "?](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/qBCO5ypO9m13MpdV66LMvZB6FUp8SIQM.png)
Answers
The reasoning presented lacks explicit explanations and logical connections between the steps, making it difficult to fully understand the intended proof strategy.
The given proof aims to show that the Separation Axioms can be derived from the Replacement Schema using a particular construction involving a formula p(x, y). Let's analyze the proof step by step:
Define the formula p(x, y) as x = yo(x).
This formula states that for each x, y pair, x is equal to the unique object y such that y is obtained by applying the operation o to x.
Define the set F as {(x, x) (x)}.
This set F contains pairs (x, x) where x is the unique object obtained by applying the operation (x) to x.
Claim: F(X) = {y (x = X)p(x, y)} = {y: (x = X)x = y^o(x)} = {x: (3x € X)o(x)} = {x X: (x)}.
This claim asserts that F(X) is equivalent to {y (x = X)p(x, y)}, which is further equivalent to {y: (x = X)x = y^o(x)}, and so on.
The proof states that since (x, y) satisfies the functional formula VaVyVz(p(x, y)^(x, z) y = z), it follows that (x, y) is a functional formula.This step emphasizes that the formula p(x, y) satisfies certain properties that make it a functional formula, which is relevant for the subsequent deductions.
Finally, the proof concludes that the Separation Axioms follow from the Replacement Schema, based on the previous steps.
For more such questions on explicit
https://brainly.com/question/30394385
#SPJ8
7
Felicia is making trail mix. The recipe calls for 3 cups pretzels and 1.5 cups of m&m's.
She wants to make 27 cups of trail mix for a birthday party. How many cups of pretzels and m&m's does she need?
Answers
Answer:
81 Cups of Pretzels and 40.5 Cups of M&M's
Step-by-step explanation:
p= Pretzels
m= M&M;s
3p+1.5m= 1
3(27)+ 1.5(27)
81 + 40.5
1)5/6 of 3/4÷7/8×2/2
2)3/2of3/4÷8/2
Answers
Step-by-step explanation:
\( (\frac{5}{6} \times \frac{3}{4} ) \times \frac{8}{7} \times 1 \\ = \frac{5}{8} \times \frac{8}{7} \\ = \frac{5}{7} \)
\(( \frac{3}{2} \times \frac{3}{4} ) \times \frac{2}{8} \\ = \frac{9}{8} \times \frac{2}{8 } \\ = \frac{9}{32} \)
Record Examination) are normally distributed with a mean of 555 and a standard
deviation of 110. Use the 68-95-99.7 Rule to find the percentage of people taking the test who score below 335.
The percentage of people taking the test who score below 335 is
Answers
Answer:
2.5%
Step-by-step explanation:
You want the percentage below 335 if the distribution is normal with a mean of 555 and a standard deviation of 110, using the empirical rule.
Z scoreThe z-score of 335 is ...
Z = (X -µ)/σ
Z = (335 -555)/110 = -220/110 = -2
DistributionThe empirical rule tells you that 95% of the distribution is between Z = -2 and Z = 2. That is, 5% of the distribution is evenly split between the tails Z < -2 and Z > 2. Half that value is in each tail.
P(X < 335) = 5%/2 = 2.5%
The percentage of people taking the test who score below 335 is 2.5%.
<95141404393>
Jack took a test and got 13/17. He took a retest and got 12/15.
Jack's grade
1. increased
2. decreased
3. stayed the same
Answers
Jack's grade increased
Jack took a test and got 13/17
13/17= 0.76
He retook the test and got 12/15
12/15= 0.8
0.76 is lesser and 0.8 is higher
Hence Jack's grade increased
Read more here
https://brainly.com/question/27536028?referrer=searchResults
#SPJ1
Consider the following game: You reach into a jar of money, and select a single bill at random to keep. There are 9 five-dollar bills, 5 ten-dollar bills, and 3 twenty-dollar bills in the jar. What should the cost of this game be in order for the game to be fair
Answers
Answer:
\(E(x)=\$9.118\)
Step-by-step explanation:
From the question we are told that:
Available bills
\(\$5=N0 9\\\\\$10=N0 5\)
\(\$20=N0 3\)
Therefore
Total Bills
\(n=5+9+3\)
\(n=17\)
Probability of selecting each bill
\(For\$5\)
\(P(\$5)=\frac{9}{17}\)
\(For\$10\)
\(P(\$10)=\frac{5}{17}\)
\(For\$20\)
\(P(\$20)=\frac{3}{17}\)
Generally the equation for Expected winning is mathematically given by
\(E(x)=\sum(X)*P(X)\)
\(E(x)=5*\frac{9}{17}+10*\frac{5}{17}+20*\frac{3}{17}\)
\(E(x)=\$9.118\)
Assortative mating is a nonrandom mating pattern where individuals with similar genotypes and/or phenotypes mate with one another more frequently than what would be expected under a random mating pattern. Researchers studying this topic collected data on eye colors of 204 Scandinavian men and their female partners. The table below summarizes the results (rows represent male eye color while columns represent female eye color). For simplicity, we only include heterosexual relationships in this exercise.
(please round any numerical answers to 4 decimal places)
Blue Brown Green Total
Blue 78 23 13 114
Brown 19 23 12 54
Green 11 9 16 36
Total 108 55 41 204
a) What is the probability that a randomly chosen male respondent or his partner has blue eyes?
b) What is the probability that a randomly chosen male respondent with blue eyes has a partner with blue eyes?
c) What is the probability that a randomly chosen male respondent with brown eyes has a partner with blue eyes?
d) What is the probability of a randomly chosen male respondent with green eyes having a partner with blue eyes?
e) Does it appear that the eye colors of male respondents and their partners are independent? Explain.
Answers
Answer:
a) P(male=blue or female=blue) = 0.71
b) P(female=blue | male=blue) = 0.68
c) P(female=blue | male=brown) = 0.35
d) P(female=blue | male=green) = 0.31
e) We can conclude that the eye colors of male respondents and their partners are not independent.
Step-by-step explanation:
We are given following information about eye colors of 204 Scandinavian men and their female partners.
Blue Brown Green Total
Blue 78 23 13 114
Brown 19 23 12 54
Green 11 9 16 36
Total 108 55 41 204
a) What is the probability that a randomly chosen male respondent or his partner has blue eyes?
Using the addition rule of probability,
∵ P(A or B) = P(A) + P(B) - P(A and B)
For the given case,
P(male=blue or female=blue) = P(male=blue) + P(female=blue) - P(male=blue and female=blue)
P(male=blue or female=blue) = 114/204 + 108/204 − 78/204
P(male=blue or female=blue) = 0.71
b) What is the probability that a randomly chosen male respondent with blue eyes has a partner with blue eyes?
As per the rule of conditional probability,
P(female=blue | male=blue) = 78/114
P(female=blue | male=blue) = 0.68
c) What is the probability that a randomly chosen male respondent with brown eyes has a partner with blue eyes?
As per the rule of conditional probability,
P(female=blue | male=brown) = 19/54
P(female=blue | male=brown) = 0.35
d) What is the probability of a randomly chosen male respondent with green eyes having a partner with blue eyes?
As per the rule of conditional probability,
P(female=blue | male=green) = 11/36
P(female=blue | male=green) = 0.31
e) Does it appear that the eye colors of male respondents and their partners are independent? Explain
If the following relation holds true then we can conclude that the eye colors of male respondents and their partners are independent.
∵ P(B | A) = P(B)
P(female=blue | male=brown) = P(female=blue)
or alternatively, you can also test
P(female=blue | male=green) = P(female=blue)
P(female=blue | male=blue) = P(female=blue)
But
P(female=blue | male=brown) ≠ P(female=blue)
19/54 ≠ 108/204
0.35 ≠ 0.53
Therefore, we can conclude that the eye colors of male respondents and their partners are not independent.
Determine which conic section is represented based on the given equation: 4x^2+9xy+4y^2-36y-125=0
Answers
The conic section of the equation 4x² + 9x +4y² - 36y - 125 = 0 is a circle
Selecting the conic section of the equationThe given equation is
4x² + 9xy + 4y² - 36y - 125 =0
The above equation is an illustration of a circle equation
The standard form of a circle equation is
(x - a)² + (y - b)² = r²
Where
(a, b) is the center
r is the radius
While the general form of the equation is
ax² + fx + by² + gy + c =0
Where c is a constant
Recall that, we have
4x² + 9x + 4y² - 36y - 125 =0
This is the general form
We can convert to the standard form as follows
Divide through by 4
x² + 2.25x + y² - 9y - 31.25 =0
Next, we complete the square of the x-terms and the y-terms
For the x-terms, we have
x² + 2.25x = x² + 2.25x + (2.25/2)² - (2.25/2)²
x² + 2.25x = (x + 2.25/2)² - (2.25/2)²
For the y-terms, we have
y² - 9y = y² - 9y + (9/2)² - (9/2)²
y² - 9y = (y - 9/2)² - (9/2)²
Substitute the new x and y terms
So, x² + 2.25x + y² - 9y - 31.25 = 0 becomes
(x + 2.25/2)² - (2.25/2)² + (y - 9/2)² - (9/2)²- 31.25 =0
Evaluate the sum of like terms
(x + 2.25/2)² + (y - 9/2)² - 3377/64 = 0
So, we have
(x + 9/8)² + (y - 9/2)² = 3377/64
Using the above as a guide, we can conclude that the conic section of the equation is a circle
Read more about conic section at
brainly.com/question/9702250
#SPJ1
HELP PLEASE!!!!!! Anaya bought a sweater that was on sale. The sweater originally cost $34.50 but was purchased for $27.60. What percentage of the original price was the discount?
Answers
Answer: 80%. Hope this helps, please consider making me Brainliest.
Step-by-step explanation:
To find the percentage, divide the sale cost by the original cost:
27.60/34.50
Let's multiply both sides by 10 to make the operation easier:
27.6/34.5 ( I eliminated the zero's because they kind of have no use) -->
276/345, now solve:
276/345 = 0.8
0.8 = 80%
The percentage is 80%.
Please answer this relatively quickly, I'm not in very much of a rush but would like to get this done.

Answers
Answer:
x=23
Step-by-step explanation:
2x-6/4 = 10
2x-6 = 10(4)
2x-6 = 40
2x = 40+6
2x = 46
x = 46/2
x = 23
Can you help me review these questions for Algebra I? I am trying to see which of my answers are possibly incorrect.
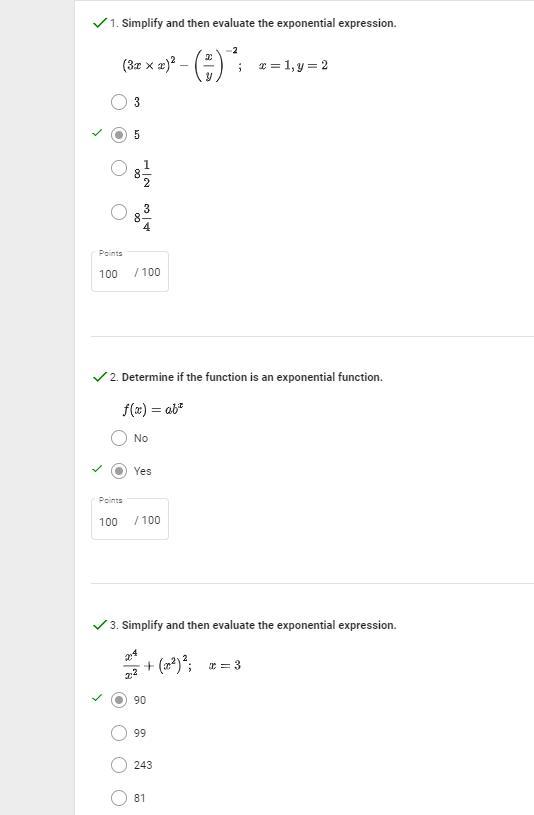
Answers
To find:
The value of given expression at x = 1 and y = 2.
\((3x\times x)^2-(\frac{x}{y})^{-2}\)Solution:
It is known that
\(a^{-b}=(\frac{1}{a})^b\)Substitute x = 1 and y = 2, in the expression and simplify as follows:
\(\begin{gathered} (3x\times x)^2-(\frac{x}{y})^{-2}=(3(1)\times1)^2-(\frac{1}{2})^{-2} \\ =(3)^2-(2)^2 \\ =9-4 \\ =5 \end{gathered}\)Thus, the answer is 5.
Many elementary school students in a school district currently have ear infections. A random sample of children in two different schools found that 16 of 40 at one school and 13 of 30 at the other had this infection. Conduct a test to answer if there is sufficient evidence to conclude that a difference exists between the proportion of students who have ear infections at one school and the other. Find the test statistic. [Suggestion: try to use a TI 83 or a similar calculator.]
Answers
Answer:
The test statistic is \(z = -0.28\)
Step-by-step explanation:
First, before finding the test statistic, we need to understand the central limit theorem and difference between normal variables.
Central Limit Theorem
The Central Limit Theorem estabilishes that, for a normally distributed random variable X, with mean \(\mu\) and standard deviation \(\sigma\), the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean \(\mu\) and standard deviation \(s = \frac{\sigma}{\sqrt{n}}\).
For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.
For a proportion p in a sample of size n, the sampling distribution of the sample proportion will be approximately normal with mean \(\mu = p\) and standard deviation \(s = \sqrt{\frac{p(1-p)}{n}}\)
Subtraction between normal variables:
When two normal variables are subtracted, the mean is the difference of the means, while the standard deviation is the square root of the sum of the variances.
A random sample of children in two different schools found that 16 of 40 at one school
This means that:
\(p_1 = \frac{16}{40} = 0.4, s_1 = \sqrt{\frac{0.4*0.6}{40}} = 0.0775\)
13 of 30 at the other had this infection.
This means that:
\(p_2 = \frac{13}{30} = 0.4333, s_2 = \sqrt{\frac{0.4333*0.5667}{30}} = 0.0905\)
Conduct a test to answer if there is sufficient evidence to conclude that a difference exists between the proportion of students who have ear infections at one school and the other.
At the null hypothesis, we test if there is no difference, that is:
\(H_0: p_1 - p_2 = 0\)
And at the alternate hypothesis, we test if there is difference, that is:
\(H_a: p_1 - p_2 \neq 0\)
The test statistic is:
\(z = \frac{X - \mu}{s}\)
In which X is the sample mean, \(\mu\) is the value tested at the null hypothesis and s is the standard error
0 is tested at the null hypothesis:
This means that \(\mu = 0\)
From the two samples:
\(p = p_1 - p_2 = 0.4 - 0.4333 = -0.0333\)
\(s = \sqrt{s_1^2+s_2^2} = \sqrt{0.0775^2+0.0905^2} = 0.1191\)
Value of the test statistic:
\(z = \frac{X - \mu}{s}\)
\(z = \frac{-0.0333 - 0}{0.1191}\)
\(z = -0.28\)
The test statistic is \(z = -0.28\)
I NEED HELP FINDING THIS ANSWER ASAP PLEASE AND THANK YOU

Answers
The coordinates of triangle after being reflected across y-axis: X"(-2, -5), Y"(-2, -2), Z"(-1, -4)
Given that the coordinates of triangle X(4, -5), Y(4, -2), Z(5, -4)
ΔXYZ is reflected across the line x = 3 and then reflects the image across the y-axis.
We need to find the coordinates of triangle after mentioned geometric transformation.
i) when ΔXYZ is reflected across the line x = 3
the coordinates of ΔX'Y'Z' are:
X'(2, -5), Y'(2, -2), Z'(1, -4)
The green triangle in the following graph.
ii) when ΔX'Y'Z' is reflected across the y-axis
the coordinates of ΔX"Y"Z" are:
X"(-2, -5), Y"(-2, -2), Z"(-1, -4)
The orange triangle in the following graph.
Therefore, the coordinates of triangle after being reflected across y-axis: X"(-2, -5), Y"(-2, -2), Z"(-1, -4)
Learn more about reflection here:
https://brainly.com/question/15487308
#SPJ1

Help and show work plz

Answers
Answer:
30
Step-by-step explanation:
If we have 4 integers that have an average of 9, then all the numbers will add up to \(9\cdot4=36\).
If we want the greatest number possible, the other 3 need to be the lowest possible.
Since they are all different, the lowest possible values of the first 3 numbers are 1, 2, and 3.
\(1 + 2 + 3 = 6\)
\(36 - 6 = 30\)
So 30 is the greatest value of one of the integers.
Hope this helped!