(3x-2)(2x2+5x-1) what is not equivalent to the product
Answers
The only option that is not an equivalent of the product of both polynomials is; C: 6x³ + 11x² − 13x + 2
What kinds of equations are there?Equations can be classified as either identities or conditioned equations. For each quantity of the variables, an identity is true. Only specific values of the variables make a conditional equation legitimate. The equals sign ("="), which separates two expressions, is a symbol for an equation.
Here,
We are given the expression;
(3x - 2)(2x² + 5x - 1)
The result of expanding the polynomial is;
6x³ + 11x² − 13x + 2
Looking at the given options as seen online, the only one that is not an equivalent of the given product is;
Option C) : 6x³ + 11x² − 13x + 2 is correct
To know more about equation , visit
brainly.com/question/12788590
#SPJ1
Related Questions
need help real baddddddddddddd

Answers
Answer:
x≥2 and x<2 : ∅
x≥2 or x<2 : All real numbers
x≤2 and x≥2 : 2
Step-by-step explanation:
the first one must follow both conditions, so no number would work.
the second one works with any number, so all real numbers.
the third one has only one condition that works, 2
If every 2 cm on a scale drawing is equal to 7 feet in real life, which lines on the drawing would be greater than 21 feet in real life? Select all that apply. A) 7 cm B) 5 cm C) 9 cm D) 12 cm
Answers
The correct answers are A) 7cm, C) 9cm and D) 12cm
Define the Conversion of units?The process of changing a given quantity that is expressed in one unit of measurement to another unit of measurement that is equivalent in value is referred to as conversion of units.
If every 2 cm on a scale drawing is equal to 7 feet in real life, then we can use proportions to find out which lines on the drawing would be greater than 21 feet in real life.
Let x be the length of a line on the scale drawing in centimeters. Then, we can set up the following proportion:
⇒ \(\frac{2cm}{7 feet} = \frac{x cm }{yfeet}\)
where y is the length of the line in real life. Solving for y, we get:
⇒ \(y = \frac{7 feet} {2cm} *x\)
⇒ \(y = 3.5 x feet\)
If we put x = 2cm (given) then, y = 7 feet
For y = 21 feet, the value of x = 6cm.
Therefore, any line on the scale drawing that is greater than 6cm in length corresponds to a length greater than 21 feet in real life.
So, the lines on the drawing that are greater than 21 feet in real life are:
A) 7cm, C) 9cm, D) 12cm
Therefore, the correct answers are A) 7cm, C) 9cm and D) 12cm
To know more about conversion, visit:
https://brainly.com/question/13016491
#SPJ1
Help please friendssssssssss

Answers
Answer: 6/(6+2x) ; (-infinity, -3) U (-3, infinity)
Step-by-step explanation:
(a) This can be read as f(x) composed of g(x). Plug in the expression given for g(x) for every x value in f(x):
(6/x)/(6/x+2)
I gave the terms in the denominator the same denominator to combine the bottom two terms into one term. 6/x + 2 is equal to 6/x + 2x/x -->
(6 +2x)/x
Do the classic keep, change, flip. \(\frac{6}{x} * \frac{x}{6+2x}\)
This simplifies to: \(\frac{6}{6+2x}\)
(b) Domain is all real numbers except for what makes the denominator equal to 0. 6 + 2x = 0 when x = -3. Therefore it is all real numbers except -3.
A student multiplies (4+5i) (3-2i) incorrectly and obtains 12-10i. What is the student's mistake? Select the two correct answers. A. They multiplied the second number by the real part of the first number. B. In the multiplication of the imaginary parts, the student forgot to square the i. C. The student has only multiplied the real parts and the imaginary parts. D. The student has added the real parts and multiplied the imaginary parts. E. The student has multiplied the second number by the imaginary part of the first number.
Answers
Answer:
B. In the multiplication of the imaginary parts, the student forgot to square the i. C. The student has only multiplied the real parts and the imaginary parts.Step-by-step explanation:
Before we figure out the student mistake, let us find the product of the complex numbers ourselves first.
(4+5i) (3-2i)
open the parenthesis
= 4(3)-4(2i)+3(5i)+5i(-2i)
= 12-8i+15i-10i²
Note that in complex number, i² = -1, hence the expression will become;
= 12-8i+15i-10(-1)
= 12-8i+15i+10
collect like terms by separating the real from imaginary part
= 12+10-8i+15i
= 22+7i
From the students answer i.e 12-10i, it can be concluded that;
In the multiplication of the imaginary parts, the student forgot to square the i and the student has only multiplied the real parts and the imaginary parts 4 and 3 to get 12
For each part, write the equation that represents the line in slope-intercept form (y = mx + b) and standard form (ax + by = c where a, b, and c are integers and a is not negative).

Answers
Answer:
Graph
\(y = -x+1\) --- Slope intercept form
\(y +x= 1\) --- Standard form
Points
\(y = 2x-2\) --- Slope intercept form
\(y -2x=-2\) --- Standard form
Step-by-step explanation:
Solving (a): The graph.
From the graph, we have:
\((x_1,y_1) = (1,0)\)
\((x_2,y_2) = (0,1)\)
First, calculate the slope
\(m = \frac{y_2 - y_1}{x_2 - x_1}\)
This gives:
\(m = \frac{1 - 0}{0 - 1}\)
\(m = \frac{1 }{- 1}\)
\(m = -1\)
The slope intercept equation is:
\(y = m(x-x_1)+y_1\)
So, we have:
\(y = -1(x-1)+0\)
\(y = -1(x-1)\)
\(y = -x+1\)
In standard form:
\(y = -x+1\)
Add x to both sides
\(y +x= x-x+1\)
\(y +x= 1\)
Solving (b): The points
From the graph, we have:
\((x_1,y_1) = (0,-2)\)
\((x_2,y_2) = (3,4)\)
First, calculate the slope
\(m = \frac{y_2 - y_1}{x_2 - x_1}\)
This gives:
\(m = \frac{4 - (-2)}{3 - 0}\)
\(m = \frac{6}{3}\)
\(m=2\)
The slope intercept equation is:
\(y = m(x-x_1)+y_1\)
So, we have:
\(y = 2(x-0)-2\)
\(y = 2(x)-2\)
\(y = 2x-2\)
In standard form:
\(y = 2x-2\)
Subtract 2x from both sides
\(y -2x= 2x-2x-2\)
\(y -2x=-2\)
Witch equation is represented by the graph below?
Answers
Solve for x:
)
(2 + 3x)
62
I
PLEASE SHOW WORK ON HOW YOU SOLVED FOR X

Answers
Answer:
x = 20
Step-by-step explanation:
These angles are vertical angles.
Vertical angles are congruent!! So we set them equal to one another.
2 + 3x = 62
-2 -2
3x = 60
---- ---
3 3
x = 20
Answer: x = 20
Concept:
Vertical angles: Pairs of opposite angles made by intersecting lines.
Vertical Angle Theorem: If 2 angles are vertical, then they are congruent.
If you cannot understand this, please refer to the attachment below for a graphical explanation.
Solve:
Given information
Angle 1 = (2 + 3x)°
Angle 2 = 62°
Set equation
Angle 1 = Angle 2
2 + 3x = 62
Subtract 2 on both sides
2 + 3x - 2 = 62 - 2
3x = 60
Divide 3 on both sides
3x / 3 = 60 / 3
\(\boxed{x=20}\)
Hope this helps!! :)
Please let me know if you have any questions

Which of the following could be the ratio between the lengths of the two legs
of a 30-60-90 triangle?
Check all that apply.
A. √2:2
B. √√3:√√3
C. √5:3
D. 1 √3
□ E. 1: √2
O F. 2:3
SUBMIT
Answers
Answer: E
Step-by-step explanation:
A scuba diver plans to go on two dives in one day. In the first, she will descend to 75 feet, and in the second she plans to descend to 43 feet. Estimate the difference between the depth of the two dives by first rounding to the nearest ten.
A) 30 feet
B) 40 feet
C) 120 feet
D) 32 feet
Answers
Answer:
A) 30
Step-by-step explanation:
If you do 75-43 feet, you get 32 feet. Round 32 to the nearest ten, and you get 30 feet
15 times 43^2 ====================
Answers
Answer:
27,735
Step-by-step explanation:
43*43=1849
1849*15=27,735
Answer:
27735Step-by-step explanation:
15 times 43^2
15 × 43² =
15 × 1849 =
27735
the current in the electronic circuit in the mobile phone was 0.12a the potential difference across the battery was 3.9V. calculate the resistance of the electronic circuit in the mobile phone
Answers
Answer:
Step-by-step explanation:
V = 3.9V
I = 0.12A
Ohm's Law, V = IR
Rearranging Ohm's Law, R = V/I
R = 3.9/0.12 = 32.5Ω
Finding the inverse of the cube of a bijective function. i About For a function f : R + R, we will define f-cube as f-cube(x) = (f(x))3 . (a) Prove that if f is a bijection, then f-cube is also a bijection. You can use the fact that for any two real numbers x and y, if x = y, then æ1/ well-defined real number. 1/3 = y1/3. Also for any real number x, x1/3 is a (b) For a bijection f, what is the inverse of f-cube? Justify your answer. Feedback?
Answers
if f is a bijection, then f-cube is also a bijection, and the inverse of f-cube is f^-1(y1/3). These results are important for understanding the properties of functions and their inverses.
Finding the inverse of the cube of a bijective function is an important step in understanding the properties of functions. To prove that f-cube is a bijection if f is a bijection, we can use the fact that for any two real numbers x and y, if x = y, then x1/3 = y1/3. This means that if f(x) = f(y), then (f(x))3 = (f(y))3, or f-cube(x) = f-cube(y). Since f is a bijection, this means that x = y, so f-cube is also a bijection.
To find the inverse of f-cube, we can use the fact that for any real number x, x1/3 is a well-defined real number. This means that if we have f-cube(x) = y, we can take the cube root of both sides to get f(x) = y1/3. Since f is a bijection, it has an inverse function f^-1, so we can apply this inverse to both sides to get x = f^-1(y1/3). This means that the inverse of f-cube is f^-1(y1/3).
In conclusion, if f is a bijection, then f-cube is also a bijection, and the inverse of f-cube is f^-1(y1/3). These results are important for understanding the properties of functions and their inverses.
Learn more about Bijection
brainly.com/question/13012424
#SPJ11
These box plots show daily low temperatures for a sample of days in two
different towns.
Town A
Town B
15 20
H
15 20 25 30
H
0 5 10 15
30
20
40
45
58
T
25 30 35 40 45 50 55 60
Degrees (F)
Click here for long description
Which statement is the most appropriate comparison of the spreads?
Answers
The most appropriate comparison of the spreads between the two towns is that Town A has a smaller spread than Town B.
To understand why this statement is true, let's analyze the box plots step by step:
1. Look at the box plots for Town A and Town B. In Town A, the box extends from approximately 15°F to 30°F, while in Town B, the box extends from around 20°F to 45°F.
2. The box in a box plot represents the interquartile range (IQR), which measures the spread of the data between the first quartile (Q1) and the third quartile (Q3). In Town A, the IQR is smaller because the range between Q1 and Q3 is narrower compared to Town B.
3. Additionally, examine the whiskers of the box plots. In Town A, the whiskers span from around 0°F to 45°F, while in Town B, the whiskers extend from approximately 15°F to 60°F.
4. The whiskers indicate the range of the data excluding any outliers. Town A has a smaller range because the whiskers cover a narrower temperature range compared to Town B.
5. Based on the observations from the box plots, it is clear that the spread of temperatures in Town A is smaller than that in Town B.
Therefore, the most appropriate comparison of the spreads is that Town A has a smaller spread than Town B.
For more such questions on comparison, click on:
https://brainly.com/question/30497593
#SPJ8
The operation is define by a+b=ab-ab
Evaluate
8 *(-4)
Answers
The answer is:
-32
Work/explanation:
Remember the integer rule:
\(\blacktriangleright\phantom{333}\sf{a\times(-b)=-ab}\)
In other words, we multiply a positive times a negative which results in a negative product.
Therefore,
8*(-4) = -32
Hence, the answer is -32.Help me with this ASAP pleaseeeeeee

Answers
Answer:
99
Step-by-step explanation:
You subtract 45 and 36 from 180
Which expression is equivalent to ?

Answers
Answer:
It's B or C, I can't see it clearly sorry!
Step-by-step explanation:
Can someone help me simplify and write in power form and show me step by step how to do it for both problem 8 and 9?

Answers
Answer:
\(\frac{-1.1x^{25} }{-1.1x^{11} }\) \(\frac{mx^{67} }{mx^{37} }\)
Step-by-step explanation:
Sine (-1.1) is the same as (-1.1) you just put them together and if the numbers are by each other you just add up the exponents. But if the question says this \(\frac{-1.1x^{2} }{-1.1x^{3} }\) than you subtract the exponents.
·\((-1.1)x^{13}X (-1.1)x^{12} = add\\\frac{-1.1x^{2} }{-1.1x^{2} } = subtract\)
Hope this helps. Have a blessed day :)
What is the expression, domain, and range for the inverse of f(x)?
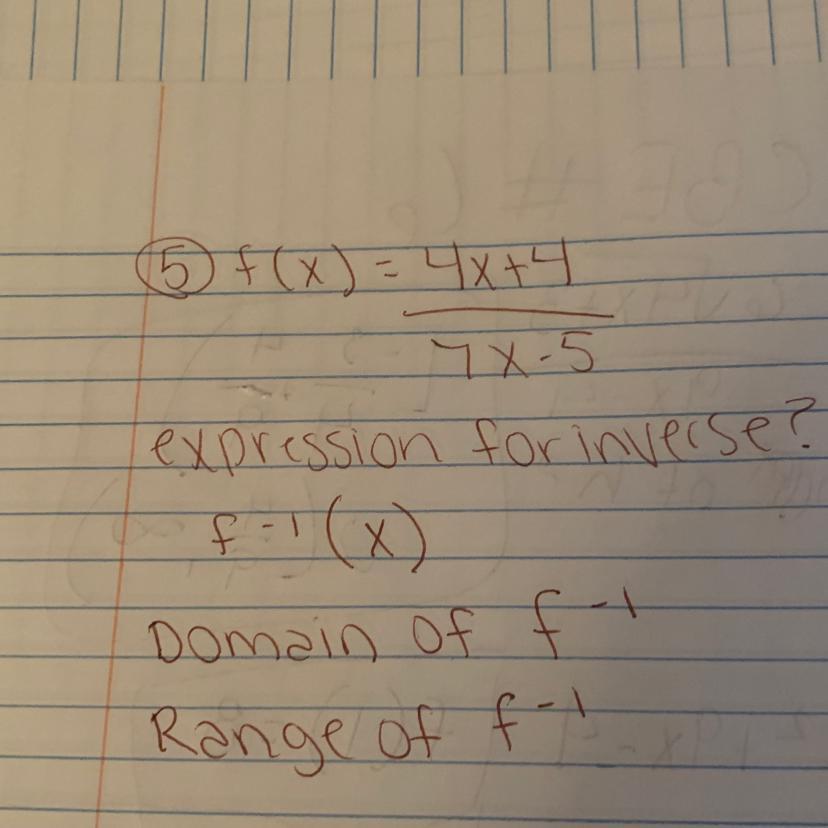
Answers
5.
\(f(x)=\frac{4x+4}{7x-5}\)1st step
Replace f(x) with y:
\(y=\frac{4x+4}{7x-5}\)2nd step:
Replace every x with a y and replace every y with an x:
\(x=\frac{4y+4}{7y-5}\)3rd step:
Solve for y:
\(\begin{gathered} x(7y-5)=4y+4 \\ 7xy-5x-4y-4=0 \\ y(7x-4)=5x+4 \\ y=\frac{5x+4}{7x-4} \end{gathered}\)4th step:
Replace y with f^-1(x)
\(f^{-1}(x)=\frac{5x+4}{7x-4}\)---------------------------------
The domain of f^-1(x) will be given by:
\(\begin{gathered} 7x-4\ne0 \\ \end{gathered}\)Since we can't divide by zero, so:
\(\begin{gathered} 7x\ne4 \\ x\ne\frac{4}{7} \\ so\colon \\ D\colon\mleft\lbrace x\in\R\colon x\ne\frac{4}{7}\mright\rbrace \\ or \\ D\colon(-\infty,\frac{4}{7})\cup(\frac{4}{7},\infty) \end{gathered}\)The range of f^-1(x) will be the domain of f(x), the domain of f(x) is given by:
\(\begin{gathered} 7x-5\ne0 \\ \end{gathered}\)Because we can't divide by zero, so:
\(\begin{gathered} 7x\ne5 \\ x\ne\frac{5}{7} \end{gathered}\)Therefore, the range of f^-1(x) is:
\(\begin{gathered} R\colon\mleft\lbrace y\in\R\colon y\ne\frac{5}{7}\mright\rbrace_{} \\ R\colon(-\infty,\frac{5}{7})\cup(\frac{5}{7},\infty) \end{gathered}\)what is an equivalent expression for 1/4x
please help ASAP.
Answers
Answer:
x/4
Step-by-step explanation:
Natasha cut a round pizza into 8 equal slices .What is the angle measure of each slice?Write and solve an equation.
Answers
Therefore 8a = 360, where a is each angle
If we divide both sides by 8 we get a = 45, so each angle is 45 degrees
A family is planning their vacation to Disney World. They will drive from a small town outside New Orleans,
Louisiana, to Orlando, Florida, a distance of 700 miles. They plan to average a rate of 55 mph. How long will this
trip take?
Answers
The time taken for the trip will be 12.7 hours.
How to calculate the value?It should be noted that time taken is calculated as:
Time = Distance / Speed
Distance = 700 miles
Speed = 55 mph
Time = 700/55
Time = 12.7 hours.
Therefore, the time taken for the trip will be 12.7 hours.
Learn more about expressions on:
brainly.com/question/22048677
#SPJ1
URGENT A bakery wanted to make their muffins more uniform in size. They reworked their equipment to do so. To test the changes, they made 25 muffins then measured each one. Which of the following should they use to determine whether or not the equipment changes worked?
Select one:
a.
mean
b.
mode
c.
range
d.
interquartile range
Answers
The bakery should use the range to determine whether or not the equipment changes have worked. The correct answer is C.
To determine whether the equipment changes made by the bakery have resulted in more uniform-sized muffins, they should use the measure of variability. The most suitable measure, in this case, would be the range.
The range is calculated by finding the difference between the maximum and minimum values in a data set. In this scenario, the bakery made 25 muffins and measured each one. By finding the range of the measurements, they can assess the spread of sizes among the muffins.
Here's how they can use the range to evaluate the effectiveness of the equipment changes:
Collect the measurements of all 25 muffins.
Determine the maximum and minimum measurements.
Calculate the range by subtracting the minimum measurement from the maximum measurement.
If the range of the muffin sizes is smaller compared to the range before the equipment changes, it suggests that the modifications have resulted in more uniform-sized muffins. Conversely, if the range remains similar or larger, it indicates that the changes might not have effectively improved the uniformity of muffin sizes.
Therefore, the bakery should use the range to determine whether or not the equipment changes have worked. The correct answer is C.
For more such answers on range
https://brainly.com/question/30389189
#SPJ11
A recycling center pays $0.10 per aluminum can and $0.05 per plastic bottle. The cheerleading squad wants to
raise $500.
Answers
Answer:
5000 aluminium cans
Step-by-step explanation:
So if the bring in ten aluminium bottles they make 1 dollar. If they bring in 50 they make 5 dollars.
If they 500 they make 50 dollars
If they bring in 5000 they make 500 dollars
Hope this helps!
PLEASE HELP !! ILL GIVE BRAINLIEST *EXTRA 40 POINTS* DONT SKIP :(( .!

Answers
Answer:
Angle 8 because it is a different measure to the other options.
Step-by-step explanation:
Congruent means the angles are the same and angle 8 is not the same as angle 7.
A car moves along a test track in the + x-direction. The velocity versus time graph below records this, with line segments L through P identifying different stages of motion. What is the average acceleration of the car between 6.0 and 8.0 seconds?

Answers
a.
For section L, the gradient is negative. So, the car is deceleratingFor section M , the gradient is zero. So, the car is moving with constant speedFor section O, the gradient is positive. So, the car is acceleratingFor section M , the gradient is zero. So, the car is moving with constant speedFor section P, the gradient is negative. So, the car is deceleratingb. The average acceleration of the car between 6.0 and 8.0 seconds is 15.0 m/s²
What is average acceleration?Average acceleration is the rate of change of velocity with time.
a. How to identify the line segments L through P?From the graph, we know that the gradient of each section is the acceleration of the car in each section.
For each section, we have the condition
gradient = 0, acceleration is zero,gradient is negative, accelereration is negative, gradient is positive, acceleration is positiveFor section L, the gradient is negative. So, the car is deceleratingFor section M , the gradient is zero. So, the car is moving with constant speedFor section O, the gradient is positive. So, the car is acceleratingFor section M , the gradient is zero. So, the car is moving with constant speedFor section P, the gradient is negative. So, the car is deceleratingb. What is the average acceleration of the car between 6.0 and 8.0 secondsThe average acceleration a = (v₂ - v₁)/(t₂ - t₁) where
t₁ = 6.0 s, v₁ = velocity at 6.0 s = 15.0 m/s, t₂ = 8.0 s, and v₁ = velocity at 8.0 s = 45.0 m/sSo, substituting the values of the variables into the equation, we have
a = (v₂ - v₁)/(t₂ - t₁)
a = (45.0 m/s - 15.0 m/s)/(8.0 s - 6.0 s)
a = (30.0 m/s)/(2.0 s)
a = 15.0 m/s²
So, the acceleration is 15.0 m/s²
Learn more about average acceleration here:
https://brainly.com/question/28850590
#SPJ1
To save for her newborn son's college education, Kelli Peterson will invest $1,500.00 at the end of each year for the next 18 years. The interest rate she expects to earn on her investment is 9%. How much money will she have saved by the time her son turns 18?
Answers
Answer:
9% of $1500 is $15 so she gains an extra $15 for each of the 18 years
$1500 in the bank each year for 18 years is $27000 after 18 years
$15 each year as well so that’s an extra $270 in the bank
The total in the bank is the sum of what she has invested and the interest so the total in the bank is $27270
Step-by-step explanation:
A spherical ball has a diameter of 10 inches. The ball has a slow leak in which the air escapes at the rate of 1.5 cubic inches per second. How long will it take the ball to deflate? Round to the nearest tenth.
Answers
It will take approximately 349.1 second for the ball with diameter of 10 to deflate.
What is volume of sphere?The formula for a sphere's volume is, V = (4/3)πr³ where V is the sphere's volume, r is its radius, and (pi) is a mathematical constant roughly equal to 3.14. According to this equation, a sphere's volume is equal to four-thirds of the sum of its radius's cube and the value of pi. In geometry and physics, this method is used to determine the volume of spherical objects like planets, balls, and bubbles.
The volume of a sphere is given as:
V = (4/3)πr³
Substituting the values:
V = (4/3)π(5)³ = 523.6 cubic inches
The rate is given as:
V = rt
Solving for t for the given rate we have:
t = V/r = 523.6/1.5 = 349.1 seconds
Hence, it will take approximately 349.1 seconds (or about 5.8 minutes) for the ball to deflate.
Learn more about volume of sphere here:
https://brainly.com/question/9994313
#SPJ1
2,17,82,257,626,1297 next one please ?
Answers
The easy thing to do is notice that 1^4 = 1, 2^4 = 16, 3^4 = 81, and so on, so the sequence follows the rule \(n^4+1\). The next number would then be fourth power of 7 plus 1, or 2402.
And the harder way: Denote the n-th term in this sequence by \(a_n\), and denote the given sequence by \(\{a_n\}_{n\ge1}\).
Let \(b_n\) denote the n-th term in the sequence of forward differences of \(\{a_n\}\), defined by
\(b_n=a_{n+1}-a_n\)
for n ≥ 1. That is, \(\{b_n\}\) is the sequence with
\(b_1=a_2-a_1=17-2=15\)
\(b_2=a_3-a_2=82-17=65\)
\(b_3=a_4-a_3=175\)
\(b_4=a_5-a_4=369\)
\(b_5=a_6-a_5=671\)
and so on.
Next, let \(c_n\) denote the n-th term of the differences of \(\{b_n\}\), i.e. for n ≥ 1,
\(c_n=b_{n+1}-b_n\)
so that
\(c_1=b_2-b_1=65-15=50\)
\(c_2=110\)
\(c_3=194\)
\(c_4=302\)
etc.
Again: let \(d_n\) denote the n-th difference of \(\{c_n\}\):
\(d_n=c_{n+1}-c_n\)
\(d_1=c_2-c_1=60\)
\(d_2=84\)
\(d_3=108\)
etc.
One more time: let \(e_n\) denote the n-th difference of \(\{d_n\}\):
\(e_n=d_{n+1}-d_n\)
\(e_1=d_2-d_1=24\)
\(e_2=24\)
etc.
The fact that these last differences are constant is a good sign that \(e_n=24\) for all n ≥ 1. Assuming this, we would see that \(\{d_n\}\) is an arithmetic sequence given recursively by
\(\begin{cases}d_1=60\\d_{n+1}=d_n+24&\text{for }n>1\end{cases}\)
and we can easily find the explicit rule:
\(d_2=d_1+24\)
\(d_3=d_2+24=d_1+24\cdot2\)
\(d_4=d_3+24=d_1+24\cdot3\)
and so on, up to
\(d_n=d_1+24(n-1)\)
\(d_n=24n+36\)
Use the same strategy to find a closed form for \(\{c_n\}\), then for \(\{b_n\}\), and finally \(\{a_n\}\).
\(\begin{cases}c_1=50\\c_{n+1}=c_n+24n+36&\text{for }n>1\end{cases}\)
\(c_2=c_1+24\cdot1+36\)
\(c_3=c_2+24\cdot2+36=c_1+24(1+2)+36\cdot2\)
\(c_4=c_3+24\cdot3+36=c_1+24(1+2+3)+36\cdot3\)
and so on, up to
\(c_n=c_1+24(1+2+3+\cdots+(n-1))+36(n-1)\)
Recall the formula for the sum of consecutive integers:
\(1+2+3+\cdots+n=\displaystyle\sum_{k=1}^nk=\frac{n(n+1)}2\)
\(\implies c_n=c_1+\dfrac{24(n-1)n}2+36(n-1)\)
\(\implies c_n=12n^2+24n+14\)
\(\begin{cases}b_1=15\\b_{n+1}=b_n+12n^2+24n+14&\text{for }n>1\end{cases}\)
\(b_2=b_1+12\cdot1^2+24\cdot1+14\)
\(b_3=b_2+12\cdot2^2+24\cdot2+14=b_1+12(1^2+2^2)+24(1+2)+14\cdot2\)
\(b_4=b_3+12\cdot3^2+24\cdot3+14=b_1+12(1^2+2^2+3^2)+24(1+2+3)+14\cdot3\)
and so on, up to
\(b_n=b_1+12(1^2+2^2+3^2+\cdots+(n-1)^2)+24(1+2+3+\cdots+(n-1))+14(n-1)\)
Recall the formula for the sum of squares of consecutive integers:
\(1^2+2^2+3^2+\cdots+n^2=\displaystyle\sum_{k=1}^nk^2=\frac{n(n+1)(2n+1)}6\)
\(\implies b_n=15+\dfrac{12(n-1)n(2(n-1)+1)}6+\dfrac{24(n-1)n}2+14(n-1)\)
\(\implies b_n=4n^3+6n^2+4n+1\)
\(\begin{cases}a_1=2\\a_{n+1}=a_n+4n^3+6n^2+4n+1&\text{for }n>1\end{cases}\)
\(a_2=a_1+4\cdot1^3+6\cdot1^2+4\cdot1+1\)
\(a_3=a_2+4(1^3+2^3)+6(1^2+2^2)+4(1+2)+1\cdot2\)
\(a_4=a_3+4(1^3+2^3+3^3)+6(1^2+2^2+3^2)+4(1+2+3)+1\cdot3\)
\(\implies a_n=a_1+4\displaystyle\sum_{k=1}^3k^3+6\sum_{k=1}^3k^2+4\sum_{k=1}^3k+\sum_{k=1}^{n-1}1\)
\(\displaystyle\sum_{k=1}^nk^3=\frac{n^2(n+1)^2}4\)
\(\implies a_n=2+\dfrac{4(n-1)^2n^2}4+\dfrac{6(n-1)n(2n)}6+\dfrac{4(n-1)n}2+(n-1)\)
\(\implies a_n=n^4+1\)
In the phrase “rise over sun” shat does “rise” indicate?
Answers
Chloe runs a farm stand that sells apples and peaches. Each pound of apples sells for
$3 and each pound of peaches sells for $4. Chloe sold 3 times as many pounds of
peaches as pounds of apples and she made $240 altogether. Graphically solve a
system of equations in order to determine the number of pounds of apples sold, x,
and the number of pounds of peaches sold, y.
pls help! plot on a line
Answers
Answer:
3x+4y=240; y=3x16 pounds of apples48 pounds of peachesStep-by-step explanation:
You want a system of equations and a graphical solution for the scenario that the weight of peaches sold (y) is 3 times the weight of apples sold (x), and the revenue from sales of apples at $3/lb and peaches at $4/lb was a total of $240.
EquationsThe revenue equation can be ...
3x +4y = 240
The relation between pounds of each fruit sold can be ...
y = 3x
GraphThe graph is attached. The solution is (x, y) = (16, 48).
16 pounds of apples and 48 pounds of peaches were sold.
__
Additional comment
We note that the 3x in the first equation can be substituted by y using the second equation. This gives 5y=240, or y = 48. Then 3x=48, so x=16. This agrees with the graphical solution, as it should.
