3x +2 = 9x + 20 for x
Answers
Answer:
Use a calculator solved :)))
Step-by-step explanation:
Answer:
x=-3
Step-by-step explanation:
3x+2=9x+20
3x-9x=20-2
-6x=18
X=-3
Related Questions
Suppose you start with one liter of vinegar and repeatedly remove 0.14 L, replace with water, mix, and repeat. a. Find a formula for the concentration after n steps. b. After how many steps does the mixture contain less than 9% vinegar?
Answers
Formula for the concentration after n steps is \(C(n) = C(0) * (0.86)^n\) and
after 11 steps, the mixture contains less than 9% vinegar.
What is concentration?
Concentration in science refers to the amount of a particular substance (the solute) that is dissolved in a given amount of a solution. It is typically expressed in units of moles per liter (M or mol/L) or as a percentage or fraction of the total solution.
a. Let C(n) be the concentration of vinegar after n steps. At each step, we remove 0.14 L of the mixture, which contains C(n) liters of vinegar. So we are left with (1 - C(n)) liters of water. We then add back 0.14 L of water, giving us a total volume of 1 liter. Therefore, the concentration after one step is:
\(C(1) = C(0) * \frac{1 - 0.14}{1}\)
where C(0) is the initial concentration of vinegar, which is 1 liter per liter or 100%. After two steps, we repeat the process:
C(2) = C(1) * \(\frac{1 - 0.14}{1}\)
Substituting the formula for C(1), we get:
C(2) = C(0) * \((\frac{1 - 0.14}{1}) * (\frac{1 - 0.14}{1})\)
or, more generally:
\(C(n) = C(0) * (0.86)^n\)
b. We want to find the smallest integer n such that C(n) < 0.09 or 9%. Substituting the formula from part (a), we get:
\(C(0) * (0.86)^n < 0.09\)
Dividing both sides by C(0), we get:
\((0.86)^n < 0.09\)
Taking the natural logarithm of both sides, we get:
n * ln(0.86) < ln(0.09)
Dividing both sides by ln(0.86), we get:
n > ln(0.09) / ln(0.86)
Using a calculator, we get:
n > 10.7
Since n must be an integer, the smallest possible value of n is 11. Therefore, after 11 steps, the mixture contains less than 9% vinegar.
To learn more about concentration visit the link:
https://brainly.com/question/17206790
#SPJ1
Using the graph determine the coordinates of the zeros of the parabola

Answers
Answer:
-5 and -The zeros of a parabola are the points on the parabola that intersect the line y = 0 (the horizontal x-axis). Since these points occur where y = 0,
NEED HELP 10-14!! SERIOUS ANSWERS ONLY 27 POINTS!! THANKS!

Answers
Answers:
10.
B: Austin did not combine -3 and -9 correctly.
11.
x=8.5
12.
2r-4s
13.
10x+3y
14.
k=2
suppose the acceleration function of an object moving along a line is given by a(t) =0.2t. find the position of the object if you know the initial velocity was v(0) =-3 and initial position was s(0) =1
Answers
Answer:
See below
Step-by-step explanation:
sf = s0 + v0 t + 1/2 at^2
1 + (-3)t + 1/2 (.2t) t^2 ( weird acceleration value)
s = 1 -3t + .1 t^3 You will need a 't' value to determine the position
For what values of x is the rational expression below undefined x-4/3x^2-65
Answers
3x^2-65=0
x^2=65/3
It is disconnected at x= + square root of (65/3) and at x= - square root(65/3)
What is the product of 3xand 2xy + 5xy 4?

Answers
(Mark me the brainliest if this has helped )
Step-by-step explanation:
option B is correct
as,
3x² × 2x³y = 6x⁵y
and
3x² × 5xy⁴ = 15x³y⁴
so,
6x⁵y + 15x³y⁴.
hope this answer helps you dear and may u have a great day ahead! take care
A total of 50 randomized samples were assigned into 5 different treatment groups in a pharmaceutical science experiment. Each group includes 10 persons (subjects). In order to test if any difference is discernible among these 5 treatments, one-way ANOVA was conducted for the study. Here are data we calculated: Sum of square between group = 232. Sum of square within group = 400.Subject Treatment 1 Treatment 2 Treatment 3 Treatment 4 Treatment 51 2
---
10ANOVA Summary Table
Source Sum of Square Degree of freedom Mean Square F
Between 232
Within 400
Totala. State null hypothesis and alternative hypothesis. b. Calculate the degree of freedom between group, and the degree of freedom within group. c. Mean squares between groups. d. Mean squares within groups.e. F ratiof. If critical value of F is 2.61, should we reject or accept the null hypothesis?g. State your conclusion for this research.
Answers
The null hypothesis is that there is no discernible difference among the 5 treatments. The alternative hypothesis is that there is a discernible difference among the 5 treatments
How to calculate the valuesDegree of freedom between groups is nothing but the number of treatments-1 i.e. 5-1=4 and degree of freedom within groups is nothing but total number of subjects- number of treatments i.e. 5*10-5=50-5=45
Mean squares between groups is calculated as follows:
Mean squares between groups= Sum of squares between groups/degrees of freedom between groups= 232/4=58
Mean squares within groups is calculated as follows:
Mean squares within groups= Sum of squares within groups/degrees of freedom within groups= 400/45= 8.89 rounded off to two decimal places
F ratio is calculated as follows:
F= Mean squares between groups/Mean squares within groups
= 58/8.89
= 6.524184477
Learn more about hypothesis on:
https://brainly.com/question/11555274
#SPJ1
What’s 2×100 +18-1+20
Answers
Answer:
it is 237
Step-by-step explanation:
Answer: 237
Step-by-step explanation:
You do not to do order of operations for this problem
2 x 100 = 200
200 + 18 = 218
218 - 1 = 217
217 + 20 = 237
Hope it helps!
Assume that when adults with smartphones are randomly selected,42 % use them in meetings or classes. If 30 adult smartphone users are randomly selected, find the probability that exactly 20 of them use their smartphones in meetings or classes.
Answers
The probability that exactly 20 out of 30 randomly selected adult smartphone users use their smartphones in meetings or classes is approximately 0.0802.
To find the probability that exactly 20 out of 30 randomly selected adult smartphone users use their smartphones in meetings or classes, we can use the binomial probability formula.
The binomial probability formula is given by:
P(X = k) = C(n, k) * p^k * (1-p)^(n-k)
Where:
P(X = k) is the probability of getting exactly k successes
n is the total number of trials (sample size)
k is the number of desired successes
p is the probability of success on a single trial
In this case:
n = 30 (number of adult smartphone users randomly selected)
k = 20 (number of users who use smartphones in meetings or classes)
p = 0.42 (probability of using smartphones in meetings or classes)
Plugging in the values into the formula:
P(X = 20) = C(30, 20) * (0.42)^20 * (1-0.42)^(30-20)
Calculating the values:
C(30, 20) = 30! / (20! * (30-20)!) = 30! / (20! * 10!) = 30,045
P(X = 20) = 30,045 * (0.42)^20 * (0.58)^10
Calculating the final result:
P(X = 20) ≈ 0.0802
Therefore, the probability is approximately 0.0802.
For more such questions on probability
https://brainly.com/question/251701
#SPJ8
29.For n ≥ 3, a pattern can be made by overlapping n circles, each of circumference 1 unit, so that each circle passes through a central point and the resulting pattern has order-n rotational symmetry.
For instance, the diagram shows the pattern where n = 7.
If the total length of visible ares is 60 units, what is n?

Answers
The value of n can be determined by finding the number of visible arcs in the pattern, which is 30 in this case.
To determine the value of n, we need to find the relationship between the total length of visible areas and the number of circles (n).
In the given pattern, each circle contributes to the visible area twice: once as its circumference and once as the overlapping part with the adjacent circles. Since the circumference of each circle is 1 unit, the visible area contributed by each circle is 2 units.
Therefore, the total length of visible areas can be expressed as 2n. Given that the total length is 60 units, we can set up the equation:
2n = 60
Solving this equation, we find:
n = 60/2 = 30
Thus, the value of n is 30.
For more questions on number of visible arcs:
https://brainly.com/question/31336038
#SPJ8
Solve the given initial-value problem.
y''' − 2y'' + y' = 2 − 24ex + 40e5x, y(0) =
1
2
, y'(0) =
5
2
, y''(0) = −
11
2
the values for the first 3 derivatives derivatives of y are 1/2, 5/2, -11/2 respectively
Answers
The given differential equation:
y''' − 2y'' + y' = 2 − 24ex + 40e5x,
y(0) = 1/2, y'(0) = 5/2, y''(0) = −11/2
Therefore, the next solution is 13/2
Differential Equation:
In mathematics, a differential equation is an equation relating one or more unknown functions to their derivatives. In applications, functions usually represent physical quantities, derivatives represent rates of change, and differential equations define the relationship between them. These relationships are common.
Now,
Given differential equation is
y''' - 2y'' +y' = 2- 24eˣ +40e⁵ˣ ------------ (1)
Auxiliary equation is m³ - 2m² +2m = 0
Now,
m(m² - 2m +2) = 0
⇒ m(m-1)² = 0
Therefore, m = 0,1,1
Therefore,
\(y_{c} = c_{1}+ c_{2} e^{x} + c_{2}x e^{x}\)
Now, we have to find the particular solution by method of undetermined coefficient.
\(y'_{y} = a + b(x^{2} e^{x} +2xe^{x} ) +5ce^{x}\)
⇒ \(y''_{p} = a + bx^{2} e^{x} +2bxe^{x} +5ce^{x}\)
⇒ \(y''_{p} = b(x^{2} e^{x} +2xe^{x}) + 2b(ex^{x}+ e^{x} +25ce^{x}\)
⇒ \(y'''_{p} = bx^{2} e^{x} +6bxe^{x} +6be^{x} +125ce^{5x}\)
Putting these values in differential equation (1), we get:
y'''(0) = 13/2
Complete Question:
Solve the given initial-value problem. y''' ? 2y'' + y' = 2 ? 24ex + 40e5x, y(0) = 1 2 , y'(0) = 5/ 2 , y''(0) = ? 13/ 2
Learn more about Differential Equation:
https://brainly.com/question/16663279
#SPJ4
SSTR = 6,750 H0: μ1=μ2=μ3=μ4
SSE = 8,000 Ha: at least one mean is different
nT = 20
Refer to Exhibit 10-16. The mean square between treatments (MSTR) equals
a. 400
b. 500
c. 1,687.5
d. 2,250
Answers
Answer:
\(SS_{total}=\sum_{j=1}^p \sum_{i=1}^{n_j} (x_{ij}-\bar x)^2 \)
\(SS_{between=Treatment}=SS_{model}=\sum_{j=1}^p n_j (\bar x_{j}-\bar x)^2 =6750\)
\(SS_{within}=SS_{error}=\sum_{j=1}^p \sum_{i=1}^{n_j} (x_{ij}-\bar x_j)^2 =8000\)
And we have this property
\(SST=SS_{between}+SS_{within}=6750+8000=14750\)
The degrees of freedom for the numerator on this case is given by \(df_{num}=k-1=4-1=3\) where k =4 represent the number of groups.
The degrees of freedom for the denominator on this case is given by \(df_{den}=df_{between}=N-K=20-4=16\).
And the total degrees of freedom would be \(df=N-1=20 -1 =19\)
We can find the \(MSTR=\frac{6750}{3}=2250\)
And \(MSE=\frac{8000}{16}=500\)
And the best answer would be:
d. 2,250
Step-by-step explanation:
We want to test the following null hypothesis:
\( H0: \mu_1 =\mu_2 =\mu_3 =\mu_4\)
If we assume that we have \(4\) groups and on each group from \(j=1,\dots,k\) we have \(k\) individuals on each group we can define the following formulas of variation:
\(SS_{total}=\sum_{j=1}^p \sum_{i=1}^{n_j} (x_{ij}-\bar x)^2 \)
\(SS_{between=Treatment}=SS_{model}=\sum_{j=1}^p n_j (\bar x_{j}-\bar x)^2 =6750\)
\(SS_{within}=SS_{error}=\sum_{j=1}^p \sum_{i=1}^{n_j} (x_{ij}-\bar x_j)^2 =8000\)
And we have this property
\(SST=SS_{between}+SS_{within}=6750+8000=14750\)
The degrees of freedom for the numerator on this case is given by \(df_{num}=k-1=4-1=3\) where k =4 represent the number of groups.
The degrees of freedom for the denominator on this case is given by \(df_{den}=df_{between}=N-K=20-4=16\).
And the total degrees of freedom would be \(df=N-1=20 -1 =19\)
We can find the \(MSTR=\frac{6750}{3}=2250\)
And \(MSE=\frac{8000}{16}=500\)
And the best answer would be:
d. 2,250
What is the distance between (-5, -8) and (-1, -16)
Answers
(4,-8)
Step-by-step explanation:
from -5 to -1 you would have to count from 1 to 4. and do the same for -8 to -16
If 3/8 of my money is $3840.00. How much did I have at first? *
A$11520.00
B$13425.00
C$12600.00
D$10750.00
E$10240.00
Answers
Answer:
E $10240.00
Step-by-step explanation:
The total amount of money is x.
3/8 × x = 3840
Multiply both sides by the reciprocal of 3/8 which is 8/3.
x = 3840 × 8/3
x = 10240
Answer: E $10240.00
Answer:
E. $10240.00
Step-by-step explanation:
$3840.00 is 3/8
so 3 ---> $3840
1 ---> $3840/3
1 ---> 1280
Then total money you had is ( 1280 * 8 ) = $10240
-12 divided by 3 5/9
Answers
your answer is 3.375
Dave runs a 10km race and beats his best time by 5%.
His best time was 60 minutes.
How long did it take him to complete the race?
Answers
Answer:
57 minutes
Step-by-step explanation:
Simply what is %5 of 60.
%5 of 60 can be found by multiplication by 0.05 x 60 giving you 3.
9. Find the sum of the first multiples of 5.
Answers
Answer:
75
Step-by-step explanation:
Use the arithmetic progression formula: S =n/2(2a + (n-1)d)
a = 5, d = 5, n = 5
S = 5/2((2(5) + (5-1)(5)) = 75
ILL GIVE BRAINLEST TO WHO EVER ANSWERS FIRST CORRECTLY I NEED THE ANSWER ASAP

Answers
Answer:
x = {2, 5 , -2}
Step-by-step explanation:
See photo for explanation:

At a baseball game, a vender sold a combined total of 183 sodas and hot dogs. The number of sodas sold was two times the number of hot dogs sold. Find the
number of sodas and the number of hot dogs sold.
Answers
Answer:
61 hot dogs
122 sodas
Step-by-step explanation:
x+x2=183
3x=183
183÷3=
61
What is the SLOPE of linear line: y = -x*
m= -1
m = 0
m = undefined
m = 1
Answers
I’m never 100% certain of my answers though but I’m pretty sure this is correct
The answer is 132 ft

Answers
Answer:
Lol, thank you for telling me this information..
A cashier worked an 8-hour day, and earned $58.00. The double number line shows the amount she earned for working different numbers of hours. For each question, explain your reasoning.
How much does the cashier earn per hour?
How much does the cashier earn if she works 3 hours? pls help me!!

Answers
Answer:
The cahier earns 7.25 an hour
and in three hours she will have 21.75
Answer:
Step-by-step explanation: IT Is The cashirs earns $7.25 each hour.She will have 21.7$
Please help me please
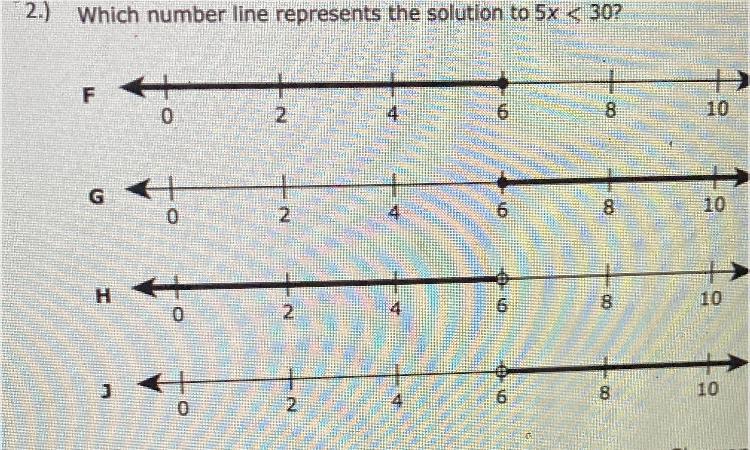
Answers
Answer:
5x<30
Open circle.
5x<30
Divide by 5
x < 6
Open circle, arrow to the left. Answer is H
Simplify all ratios and keep them as improper fractions
If arc cos = -8/17 and arc sin is negative, then arcsin is _____ and arctan is ______
Answers
To find arcsin, we need to use the identity:
sin(arcsin(x)) = x
Since arcsin is negative, sin(arcsin) is also negative. Therefore, we can say:
sin(arcsin) = -sqrt(1 - (cos)^2)
where (cos)^2 = 8/17
Substituting, we get:
sin(arcsin) = -sqrt(1 - (8/17))
Simplifying, we get:
sin(arcsin) = -sqrt(17/17 - 8/17)
Simplifying further, we get:
sin(arcsin) = -sqrt(9/17)
Therefore, arcsin = -sqrt(9/17)
To find arctan, we need to use the identity:
tan(arctan(x)) = x
Substituting, we get:
tan(arctan) = -8/17
Therefore, arctan = -8/17
So, arcsin is -sqrt(9/17) and arctan is -8/17.
The instructor noted the following scores on the last quiz of the semester for 8 students. Find the range of this data set 59,61,83,67,81,80,81,100
Answers
answer: the range is 41.
to find the range of this data set, we first need to find the minimum and maximum values - which are 59 and 100.
then we subtract the minimum from the maximum.
59 - 100 = 41.
Aiden leans a 30-foot ladder against a wall so that it forms an angle of 78^{\circ} ∘ with the ground. What’s the horizontal distance between the base of the ladder and the wall? Round your answer to the nearest hundredth of a foot if necessary.
Answers
Answer:
6.2 approx i believe
Step-by-step explanation:
Given: AAEB and ADFC, ABCD, AE || DF, EB || FC, AC = DB
Prove: AEAB AFDC

Answers
By proving that ΔEAB and ΔFDC have congruent corresponding angles and proportional corresponding sides, we can conclude that ΔEAB ≅ ΔFDC.
Proving that Triangles are EqualGiven:
- Triangle ΔAEB and ΔDFC
- Line ABCD is straight (implies AC and BD are collinear)
- AE is parallel to DF
- EB is parallel to FC
- AC = DB
To prove: ΔEAB ≅ ΔFDC
Recall that:
AE || DF
EB || FC
AC = DB
AE || DF, EB || FC (Parallel lines with transversal line AB)
Corresponding angles are congruent:
∠AEB = ∠DFC (Corresponding angles)
∠EAB = ∠FDC (Corresponding angles)
Corresponding sides are proportional:
AE/DF = EB/FC (Corresponding sides)
AC/DB = BC/DC (Corresponding sides)
AC = DB
BC = DC (Equal ratios)
ΔEAB ≅ ΔFDC (By angle-side-angle (ASA) congruence)
∠EAB = ∠FDC
∠AEB = ∠DFC
AC = DB, BC = DC
Therefore, by proving that ΔEAB and ΔFDC have congruent corresponding angles and proportional corresponding sides, we can conclude that ΔEAB ≅ ΔFDC.
Learn more about triangles here:
https://brainly.com/question/30104125
#SPJ1
A Bakery made 423 sandwiches in one day. What is that number rounded to the nearest hundred sandwiches?
Answers
Answer: 400
Step-by-step explanation:
how do you find questions that are unanswered and about math help me please and thanks
Answers
you can find some if you scroll down on the page we're on.
They should kinda look like questions in little boxes.
They'll be under the header "New Questions in Mathematics"
don't feel bad, it took me a while too, they kinda blend in & no one would scroll down that far. I hoped this help you or someone else
have a great day :D
Swimming Pool On a certain hot summer's day, 685 people used the public swimming pool. The daily prices are $1.25 for children and $2.50 for adults. The receipts for admission totaled $1352.50. How many children and how many adults swam at the public pool that day?
Answers
Answer:
120 children and 388 adults bought tickets for the swimming pool. Explanation: Create two simultanous equations:.