2(4x-1)+3=7
i'm little confused on this
Answers
Answer:
x = \(\frac{3}{4}\)
Step-by-step explanation:
Since you cannot subtract -1 from 4x, you multiply 2 × 4x = 8x
Now, you have 8x - 1 + 3 = 7
Seperate the 8x from the other numbers
8x = 1 - 3 + 7 ---> 6
8x = 6
Now simplify
x = \(\frac{6}{8}\) <----- to reduce, divide the numerator and denominator by 2
Hence,
x = \(\frac{3}{4}\)
Related Questions
Given that f=ax+bt2 +c is an equation where x is the distance and t is time.find the dimensions of the expression (axb)/(bt2)
Answers
The given expression (axb)/(bt2) is a dimensionless quantity.
To find the dimensions of the expression (axb)/(bt2),
where f = ax + bt2 + c,
we will consider the units of each term in the equation.
Let's assume the unit of distance (x) to be meters (m) and the unit of time (t) to be seconds (s).
Therefore, the units of each term are as follows:
ax has units of (m) * (unit of a)bt2 has units of (s2) * (unit of b)c has units of (unit of c)
The final expression can be written as:
(axb)/(bt2) = a/m * b/ s2
The above expression is a dimensionless quantity.
This is because the dimensions of both the numerator and denominator cancel out each other.
Therefore, the dimensions of (axb)/(bt2) are dimensionless.
Note: A dimensionless quantity does not have any physical dimension or units.
It is also known as a pure number.
A physical quantity is expressed as the product of a numerical value and a physical unit. The unit of a physical quantity provides the scale or reference standard for measuring that quantity.
Dimensional analysis is a powerful tool for solving problems in physics.
It involves checking the consistency of units in an equation to ensure that it is physically meaningful. By using the correct units and dimensions, we can easily convert from one unit to another and avoid errors in calculations.
To know more about dimensionless visit :
brainly.com/question/1625902
#SPJ11
Random variables X and Y have the joint PMFPX,Y(x,y) = c|x+y| x=-2,0,2; y=-1,0,1. 0 otherwise1) what is the value of constant c?2)what is P[YX]?4)what is P[Y=X]?5)what is P[X<1]?
Answers
Random variables X and Y have the joint PMFPX,Y(x,y) = c|x+y| x=-2,0,2; y=-1,0,1 the answers are: 1. the value of the constant c is 1/12, 2. P[Y=X] = P[X=0, Y=0] = 0, and 3.P[X<1] is equal to 1/2.
1. To find the value of the constant c, we need to ensure that the sum of the joint probabilities over all possible values equals 1.
The given joint probability mass function (PMF) P(X,Y) is:
P(X=-2, Y=-1) = c|-2+(-1)| = c|(-3)| = 3c
P(X=-2, Y=0) = c|-2+0| = c|(-2)| = 2c
P(X=-2, Y=1) = c|-2+1| = c|(-1)| = c
P(X=0, Y=-1) = c|0+(-1)| = c|(-1)| = c
P(X=0, Y=0) = c|0+0| = c|0| = 0
P(X=0, Y=1) = c|0+1| = c|1| = c
P(X=2, Y=-1) = c|2+(-1)| = c|1| = c
P(X=2, Y=0) = c|2+0| = c|2| = 2c
P(X=2, Y=1) = c|2+1| = c|3| = 3c
Summing up these probabilities, we get:
3c + 2c + c + c + 2c + 3c = 12c
For this sum to equal 1, we have:
12c = 1
c = 1/12
Therefore, the value of the constant c is 1/12.
2. To find P[Y|X], we need to calculate the conditional probability of Y given X. Since the PMF is given, we can directly read the values:
P[Y=-1|X=-2] = c|-2+(-1)| = c|(-3)| = 3c = 3/12 = 1/4
P[Y=0|X=-2] = c|-2+0| = c|(-2)| = 2c = 2/12 = 1/6
P[Y=1|X=-2] = c|-2+1| = c|(-1)| = c = 1/12
Similarly, for other values of X, we can calculate the conditional probabilities.
P[Y=X] refers to the probability that Y is equal to X. Looking at the given PMF, we can see that the only case where Y=X is when X=0, as no other values in the PMF have the same value for X and Y.
Therefore, P[Y=X] = P[X=0, Y=0] = 0.
3. Finally, to find P[X<1], we need to sum up the probabilities for all Y values where X<1:
P[X<1] = P[X=-2, Y=-1] + P[X=-2, Y=0] + P[X=0, Y=-1] + P[X=0, Y=0]
= 3/12 + 2/12 + 1/12 + 0 = 6/12 = 1/2.
Therefore, P[X<1] is equal to 1/2.
To learn more about variables from the given link
https://brainly.com/question/28248724
#SPJ4
MERVIL PRACTILE The method of tree ring dating gave the following years A.D. for an archaeological excavation site. Assume that the population of x values has an approximately normal distribution 1,194 1,278 1,292 1,313 1,268 1,316 1,275 1,317 1,275 LAUSE SALT (a) Use a calculator with mean and standard deviation keys to find the sample mean year x and sample standard deviation s. (Round your answers to four decimal places) A.D (b) Find a 90% confidence interval for the mean of all tree ring dates from this archaeological site. (Round your answers to the nearest whole number) lower limit A.D. upper limit A.D. Need Help?
Answers
The lower limit is 1269 A.D., and the upper limit is 1291 A.D.
(a) The method of tree ring dating gave the following years A.D. for an archaeological excavation site. Assume that the population of x values has an approximately normal distribution;194, 1,278, 1,292, 1,313, 1,268, 1,316, 1,275, 1,317, 1,275.Let x be the sample mean and s be the sample standard deviation. Using the calculator, we get:x = 1280.1111 (rounded to four decimal places)s = 18.7342 (rounded to four decimal places)Therefore, the sample mean year x is 1280.1111 A.D., and the sample standard deviation s is 18.7342 A.D.
(b) 90% Confidence Interval The formula for the confidence interval for the mean of a normal distribution with known standard deviation is: CI = x ± Zα/2 (σ/√n)where CI is the confidence interval, x is the sample mean, Zα/2 is the critical value from the standard normal distribution for a given level of confidence (α), σ is the known population standard deviation, and n is the sample size. Since the sample size is small and the population standard deviation is unknown, we use the t-distribution instead of the standard normal distribution. The formula becomes: CI = x ± tα/2 (s/√n)where tα/2 is the critical value from the t-distribution for a given level of confidence (α) and n - 1 degrees of freedom. Using a t-table with 8 degrees of freedom and a level of significance of 0.1 (because we want a 90% confidence interval), we get:t0.05 = 1.85955t0.05 = -1.85955, The sample mean is x = 1280.1111 A.D., the sample standard deviation is s = 18.7342 A.D., and the sample size is n = 9.So, the confidence interval is:
CI = 1280.1111 ± 1.85955 (18.7342/√9)CI = 1280.1111 ± 11.06677CI = (1269, 1291)
Hence, the lower limit is 1269 A.D., and the upper limit is 1291 A.D.
To know more about standard deviation visit:
https://brainly.com/question/475676
#SPJ11
okay I bearly even know what a function is and this is practice I have a test monday!?

Answers
Answer:
A.
Step-by-step explanation:
A. because an input cannot have two outputs. However, two different inputs can have the same output.
What is the answer to 71270-32425
Answers
Answer: 38845
Step-by-step explanation:
Answer:
38,845
Step-by-step explanation:
Prove : ∣u⋅v∣⩽∣u∣∣v∣
∣u+v∣⩽∣u∣+∣v∣
Answers
Both of the given inequalities (∣u⋅v∣⩽∣u∣∣v∣ and ∣u+v∣⩽∣u∣+∣v∣) have been proved using the Cauchy-Schwarz inequality and the triangle inequality, respectively.
To prove the inequalities, let's consider vectors u and v in a vector space.
Proof: ∣u⋅v∣⩽∣u∣∣v∣
We start by using the Cauchy-Schwarz inequality:
∣u⋅v∣ ⩽ ∣u∣∣v∣
This inequality is a direct consequence of the Cauchy-Schwarz inequality, which states that for any vectors u and v in a vector space:
∣u⋅v∣ ⩽ ∣u∣∣v∣
Therefore, the first inequality is proven.
Proof: ∣u+v∣⩽∣u∣+∣v∣
To prove this inequality, we can use the triangle inequality:
∣u+v∣ ⩽ ∣u∣ + ∣v∣
The triangle inequality states that for any vectors u and v in a vector space:
∣u+v∣ ⩽ ∣u∣ + ∣v∣
Hence, the second inequality is proven.
Both of the given inequalities (∣u⋅v∣⩽∣u∣∣v∣ and ∣u+v∣⩽∣u∣+∣v∣) have been shown to be true using the Cauchy-Schwarz inequality and the triangle inequality, respectively.
To learn more about Cauchy-Schwarz inequality visit:
brainly.com/question/30402486
#SPJ11
Solve the following system of equations using substitution (Enter your answer as an ordered pair, including the parentheses and comma.)
-3x+6y=12
2y=x+4
Answers
The system of equations has infinite solutions, both equations represent the same line.
How to solve the system of equations?
Here we have the following system of equations:
-3x+6y=12
2y=x+4
And we want to solve this by substitution, first, we can rewrite the first equation as:
-3x + 3*(2y) = 12
Now we can substitute the second equation 2y = x + 4 in the parenthesis, we will get:
-3x + 3*(x + 4) = 12
Now we can solve this for x.
-3x + 3x + 12 = 12
12 = 12
So this is true for any value of x, which means that both equations represent the same line (thus the system has infinite solutions).
Learn more about systems of equations:
https://brainly.com/question/13729904
#SPJ1
An object is moving at a speed of 4 meters per month. Express this speed in inches
per hour. Round your answer to the nearest hundredth.
*Note: you must use these exact conversion factors to get this question right.
Distance / length
Time
1 foot (ft) = 12 inches (in)
1 minute (min) = 60 seconds (sec)
1 yard (yd) = 3 feet (ft)
1 hour (hr) = 60 minutes (min)
1 mile (mi) = 5280 feet (ft)
1 day (day) = 24 hours (hr)
1 meter (m) = 100 centimeters (cm)
1 week (week) = 7 days (days)
1 kilometer (km) = 1000 meters (m)
1 month (month) = 30 days (days)
1 inch (in) = 2.54 centimeters (cm)
1 year (year) = 365 days (days)
1 foot (ft) = 0.305 meters (m)
1 mile (mi) = 1.609 kilometers (km)
Answers
Answer:
0.22inches/hourStep-by-step explanation:
Given the speed of an object to be 4metres/month, we are to express the speed in inches/hour.
First we will need to convert 4meters to inches
From the conversion factors given,
1 foot (ft) = 0.305 meters (m)
x ft = 4metres
cross multiply
x * 0.305 = 4*1
x = 4/0.305
x = 13.115ft
4 metres = 13.115ft
Then we will convert 13.115ft to inches
From the conversion factors,
1 foot (ft) = 12 inches (in)
13.115ft = y
cross multiply
y = 13.115*12
y = 157.377 inches
Hence 4 metres = 157.77inches.
For 1 month to hour
First we need to convert month to days and from the conversion factor
1 month = 30 days
Next is to convert 30days to hours
Since 1 day = 24hours
30days = z
z = 30* 24
z = 720hours
Hence 1 month = 720hours
On converting 4metres/month to inches/hour
4metres/month = 157.77inches/720hours
4metres/month = 0.219inches/hour
Hence the speed of the object in inches per hour to the nearest hundredth is 0.22inches/hour
29 Transformations of linear functions C8G
Find g(x), where g(x) is the translation 1 unit right of f(x) = 7x + 4.
Write your answer in the form mx + b, where m and b are integers.
g(x) =
Submit
Answers
Step-by-step explanation:
please review the attachment

Is 1 1 2 3 5 8 an arithmetic sequence?
Answers
No, 1 1 2 3 5 8 is not an arithmetic sequence. An arithmetic sequence is a sequence of numbers in which each term is obtained by adding a constant to the previous term.
Thus, the difference between successive terms is the same. In the given sequence, the difference between terms 1 and 2 is 0, between terms 2 and 3 is 1, between terms 3 and 5 is 2, and between terms 5 and 8 is 3. Therefore, the difference between successive terms is not the same and hence, 1 1 2 3 5 8 is not an arithmetic sequence.
Learn more about Arithmetic Sequence here:
https://brainly.com/question/6561461
#SPJ4
which equation can be used to find the value of x?

Answers
Answer:
3rd
Step-by-step explanation:
corner A + corner B + corner C = 180 degrees (in triangle)
so the correct answer is:
x + 68 + 72 = 180
what value of x makes this inequality true?
x+9 < 4x
Answers
Answer:
X>3
Step-by-step explanation:
X+9<4X
x-x+9<4x-x
9<3x
3<x
PLEASE HELP ME TO DO FULL SOLVE OF THIS QUESTION when sunayana purcased a video-game she paid Rs 162.50 as VAT at the rate of 13%. find its cost without levying VAT. Rs 1250 is answer please how to take out this answer
Answers
Answer:
Rs. 1250
Step-by-step explanation:
\(x\) is the cost of the video-game without VAT.
VAT is 162.5 at the rate of 13%.
13% of \(x\) is the VAT.
\(13/100 \times x = 162.5\)
\(0.13 \times x =162.5\)
\(x=162.5 \div 0.13\)
\(x=1250\)
Three friends, Jessica, Tyree, and Ben, are collecting canned food for a culinary skills class. Their canned food collection goal is represented by the expression 8x^2 - 4xy + 8. The friends have already collected the following number of cans:
Jessa: 5xy + 17
Tyree: x^2
Ben: 4x^2 - 8
Part A: Write an expression to represent the amount of canned food collected so far by the three friends. Show all your work! (5 points)
Part B: Write an expression that represents the number of cans the friends still need to collect to meet their goal. Show all you work! (5 points)
Answers
(a) The expressiοn that represents amοunt οf canned fοοd cοllected by the three friends = 5x² + 5xy - 9
(b) the expressiοn that represents number οf cans which are still need tο cοllect is = 3x² - 9xy + 17
What is expressiοn?An expressiοn is a way οf writing a statement with mοre than twο variables οr numbers with οperatiοns such as additiοn, subtractiοn, multiplicatiοn, and divisiοn.
Example: 2 + 3x + 4y = 7 is an expressiοn.
It is given that,
number οf cans cοllected by Jessa = 5xy + 17
number οf cans cοllected by Tyree = x²
number οf cans cοllected by Ben = 4x² - 8
Part(a)
tοtal number οf cans cοllected by three friends = cans cοllected by Jessa + Tyree + Ben
= 5xy + 17 + x² + 4x² - 8
= 5x² + 5xy - 9
Part(b)
the gοal οf fοοd cans cοllected = 8x² − 4xy + 8
Sο, the number οf fοοd cans still left tο cοllect = gοal - (number οf cans cοllected)
= (8x² − 4xy + 8) - (5x² + 5xy - 9)
= 8x² - 5x² - 4xy − 5xy + 8 + 9
= 3x² - 9xy + 17
Therefοre,
(a) The expressiοn that represents amοunt οf canned fοοd cοllected by the three friends = 5x² + 5xy - 9
(b) the expressiοn that represents number οf cans which are still need tο cοllect is = 3x² - 9xy + 17
Learn more about Expressions here
brainly.com/question/28987492
#SPJ1
At the Sunnyvale Play House, the price for an adult ticket is $12 and the price of a child's ticket is $6. For Saturday night's play, 125 tickets were sold, totaling $1,140. Which system of equations correctly represents this situation where a represents the number of adult tickets sold for Saturday night's play and c represents the number of child tickets sold?
Answers
The system of equations that represents this situation will be a + c = 125 and 12a + 6c = 1140.
Price of children's ticket = $6Price of adult's ticket = $12Total amount made = $1140Total tickets sold = 125Number of adults = aNumber of children = c
Therefore, the equation that can be used in solving the question will be:
a + c = 125
12a + 6c = 1140
The equation above will give the values needed.
Read related link on:
https://brainly.com/question/22722918
Solve the equation for the y–value and choose whether it is a direct variation or inverse variation
-4x + y = 0

Answers
Answer: Choice C
y = 4x
Direct variation
=====================================================
Explanation:
We add 4x to both sides to isolate y. That leads to y = 4x
This is a direct variation equation because it's in the form y = kx, for some constant k.
1.
The distance from the Sun to Mercury is 3.598. 10^7
miles. The distance from the Sun to Neptune is
2.798. 10^9 miles. How far is Mercury from Neptune?
Write your answer in scientific notation.
Answers
Answer:
Exponente positivo
Potencias de 10
Escribe estos números en forma ordinaria:
7'3·103; 4'724·108; 8'24·105
Notación científica. Orden de magnitud. Comparaciones
Expresa en notación científica las siguientes cantidades e indica su orden de magnitud.
235'74; 1985; 12 billones; 320 millones; 37.800.000.000; 220.000.
La desaparición de los dinosaurios ocurrió hace 65 millones de años, aproximadamente 108 años. Por ello hemos situado la D debajo de la potencia correspondiente:
El nacimiento del Universo (U) ocurrió hace 15 mil millones de años . Sitúa U en la casilla que le corresponde. Haz lo mismo con:
El califato cordobés de Abderramán (A): aproximadamente 800 años.
El control, del fuego (F): hace 600.000 años.
Aparición del hombre de Cromagnon (C): 30.000 años.
El nacimiento de la Tierra: (T): 4.5 mil millones de años.
El primer paso del hombre en la Luna (L): hace una veintena de años.
El primer paso del hombre en la Tierra (H): tres millones de años
La invención de la imprenta por Gutenberg (G): hace 550 años.
La nebulosa "Triangulum" está a 1'4·1022 metros de la Tierra. Escribe esta distancia en forma ordinaria.
Step-by-step explanation:
A triangle on a coordinate plane is translated according to the rule Ias(x, y). Which is another way to write this rule?
(x,y) - (X-3.y + 5)
(x, y) - (x-3.y-5)
(x,y) - (x + 3y-5)
(x,y) - (x + 3. y + 5)
Answers
suppose you are playing poker with a non-standard deck of cards. the deck has 5 suits, each of which contains 12 values (so the deck has 60 cards total). how many 6-card hands are there, where you have at least one card from each suit?
Answers
The number of 6-card hands in which at least one card from each suit is equal to 8,184,220.
Total number of 6-card hands that can be formed from a deck of 60 cards is,
Using combination formula,
C(60, 6) = 50,063,860
Now, subtract the number of 6-card hands that do not contain at least one card from each suit.
There are 5 ways to choose the suit that will be missing from the hand.
Once this suit is chosen, there are 48 cards remaining in the other suits.
Choose 6 cards from this set, so the number of 6-card hands that do not contain any cards from the chosen suit is,
C(48, 6) = 12,271,512
Overcounted the number of hands that are missing more than one suit.
There are C(5, 2) ways to choose 2 suits that will be missing from the hand.
Once these suits are chosen, there are 36 cards remaining in the other 3 suits.
Choose 6 cards from this set, so the number of 6-card hands that do not contain any cards from the chosen suits is,
C(36, 6) = 1,947,792
We cannot have a 6-card hand that is missing more than 2 suits.
3 suits with no cards in the hand, which is not allowed.
Number of 6-card hands that have at least one card from each suit is,
C(60, 6) - 5×C(48, 6) + C(5, 2)×C(36, 6)
=50,063,860 - 5× 12,271,512 + 10 × 1,947,792
= 50,063,860 -61,357,560 + 19,477,920
= 8,184,220
Therefore, there are 8,184,220 of 6-card hands that have at least one card from each suit.
Learn more about cards here
brainly.com/question/15699808
#SPJ4
Help plzz need the answer and that explanation plz don't send a file I need help with question 21!!

Answers
Answer:
No, they cannot be becuase the points are too different- no same numerical values.
Total expenditures in a country (in billions of dollars) are increasing at a rate of f(x) = 8.22X + 87 23, where x = 0 corresponds to the year 2000. Total expenditures were $1590.5 billion in 2002 a. Find a function that gives the total expenditures x years after 2000 b. What will total expenditures be in 2017? a. What is the function for the total expenditures? F(x)= (Simplify your answer Use integers or decimals for any numbers in the expression) billion. b. In 2017, total expenditures will be s (Type an integer or a decimal)
Answers
a. The function for the total expenditures is F(x) = 4.11x² + 87.23x + 1386.52
b. In 2017, total expenditures will be 3669.57 billion dollars.
a. Since the rate of increase of total expenditures is given as f(x) = 8.22x + 87.23, the function that gives the total expenditures x years after 2000 can be found by integrating the rate of increase:
F(x) = ∫ f(x) dx = 4.11x² + 87.23x + C
Since the total expenditures were $1590.5$ billion in 2002, we can use this information to find the constant $C$:
F(2) = 4.11(2)² + 87.23(2) + C = 1590.5
Solving for C, we get:
C = 1386.52
Therefore, the function that gives the total expenditures x years after 2000 is:
F(x) = 4.11x² + 87.23x + 1386.52 (in billions of dollars)
b. To find the total expenditures in 2017, we need to substitute x = 17 in the function F(x):
F(17) = 4.11(17)² + 87.23(17) + 1386.52≈ 3669.57
Therefore, the total expenditures in 2017 will be approximately 3669.57 billion dollars.
Learn more about expenditure at https://brainly.com/question/15122314
#SPJ11
A residual is the difference between _______.
Answers
A residual is the difference between "the measured and predicted values of the quantity of interest".
What is residuals?In regression analysis, a residual would be the difference between an observable and anticipated value.
The formula is;
Residual = Observed value – Predicted value
Some key features regarding the residuals are-
The purpose of linear regression would be to quantify the relationship among one or so more predictor variables one and or more response variables. Linear regression selects the line that best "fits" the data, defined as least squares regression line, to do this. This line generates a prediction for every observation in the dataset, however it is improbable that the regression line's prediction would perfectly match its observed value.The residual is the discrepancy between the predicted and the observed value. The residuals for every observation would represent the vertical distance between both the observation as well as the regression line if we plotted the observed values then overlaid the fitted regression line.To know more about the residual, here
https://brainly.com/question/1447173
#SPJ4
3 -2 -14
12
543-2
B
Which function could be a stretch of the exponential
decay function shown on the graph?
O f(x) = 2(6)*
O f(x) = -1/-(6)
○ f(x) = 2 [²/2] *
© f(x) = 2 ( 1 )
Answers
The stretch of an exponential decay function is y = 2(1/6)^x
Which is a stretch of an exponential decay function?An exponential function is represented as
y = ab^x
Where
a = initial valueb = growth/decay factorIn this case, the exponential function is a decay function
This means that
The value of b is less than 1
An example of this is, from the list of option is
y = 2(1/6)^x
Hence, the exponential decay function is y = 2(1/6)^x
Read more about exponential function at
brainly.com/question/2456547
#SPJ1
The local population of kangaroos is represented by the following function, P(t)=−2t
5
+5t
4
+80t
3
+1 where P is the population and t is time in years. i. Find the critical points of the function. [2 marks] ii. In how many years will the population reach a maximum? [1 mark] iii. What is the maximum population?
Answers
The maximum population is -255.
To find the critical points of the function \(P(t) = -2t^5 + 5t^4 + 80t^3 + 1,\)we need to find the values of t where the derivative of the function is equal to zero.
i. Find the critical points:
To find the derivative of the function, we can differentiate each term separately:
\(P'(t) = -10t^4 + 20t^3 + 240t^2\)
Now, we set P'(t) equal to zero and solve for t:
\(-10t^4 + 20t^3 + 240t^2 = 0\\\)
Factoring out common terms, we get:
\(t^2(-10t^2 + 20t + 240) = 0\)
We have two factors:
\(t^2 = 0 -- > t = 0 (multiplicity 2)\)
\(-10t^2 + 20t + 240 = 0Dividing both sides by -10, we get:t^2 - 2t - 24 = 0\\\)
This quadratic equation can be factored as:
(t - 4)(t + 6) = 0
Setting each factor equal to zero:
t - 4 = 0 --> t = 4
t + 6 = 0 --> t = -6
Therefore, the critical points of the function are t = 0 (multiplicity 2), t = 4, and t = -6.
ii. In how many years will the population reach a maximum?
To determine when the population reaches a maximum, we need to analyze the behavior of the function at the critical points.
From the critical points we found, t = 0 (multiplicity 2), t = 4, and t = -6, we can see that t = 0 occurs twice, indicating a potential point of inflection rather than a maximum or minimum.
To determine the maximum point, we need to check the second derivative, which will help us identify whether the critical points are maximum or minimum points.
The second derivative of P(t) is obtained by differentiating P'(t):
\(P''(t) = -40t^3 + 60t^2 + 480t\\\)
Evaluating P''(t) at the critical points:
P''(0) = 0
P''(4) = 3520
P''(-6) = 2880
Since P''(4) > 0 and P''(-6) > 0, it means the function is concave up at t = 4 and t = -6. Therefore, the population reaches a maximum at t = 4.
iii. What is the maximum population?
To find the maximum population, we substitute the value of t = 4 into the original function P(t):
\(P(4) = -2(4)^5 + 5(4)^4 + 80(4)^3 + 1\)
Simplifying this expression, we get:
\(P(4) = -2(1024) + 5(256) + 80(64) + 1P(4) = -2048 + 1280 + 512 + 1P(4) = -2048 + 1793P(4) = -255\)
Therefore, the maximum population is -255.
To know more function click-
https://brainly.com/question/25638609
#SPJ11
Find the rate of change (slope) given the set of data points below.
10, 19
4, 17
-2, 15
-8, 13
Answers
1/3 is the rate of change (slope) given the set of data points below
To find the rate of change (slope) given the set of data points, we can use the formula for slope:
slope = (change in y) / (change in x)
Using the given points:
Point 1: (10, 19)
Point 2: (4, 17)
Point 3: (-2, 15)
Point 4: (-8, 13)
We can calculate the slope between each pair of points:
Slope between Point 1 and Point 2:
slope = (17 - 19) / (4 - 10) = -2 / -6 = 1/3
Slope between Point 2 and Point 3:
slope = (15 - 17) / (-2 - 4) = -2 / -6 = 1/3
Slope between Point 3 and Point 4:
slope = (13 - 15) / (-8 - (-2)) = -2 / -6 = 1/3
The rate of change (slope) between these points is consistent and equal to 1/3.
Know more about slope here:
https://brainly.com/question/16949303
#SPJ8
Triangle 1 is a scale drawing of Triangle 2, as shown below.
Based on the information shown in these triangles, what is the length of the side x?
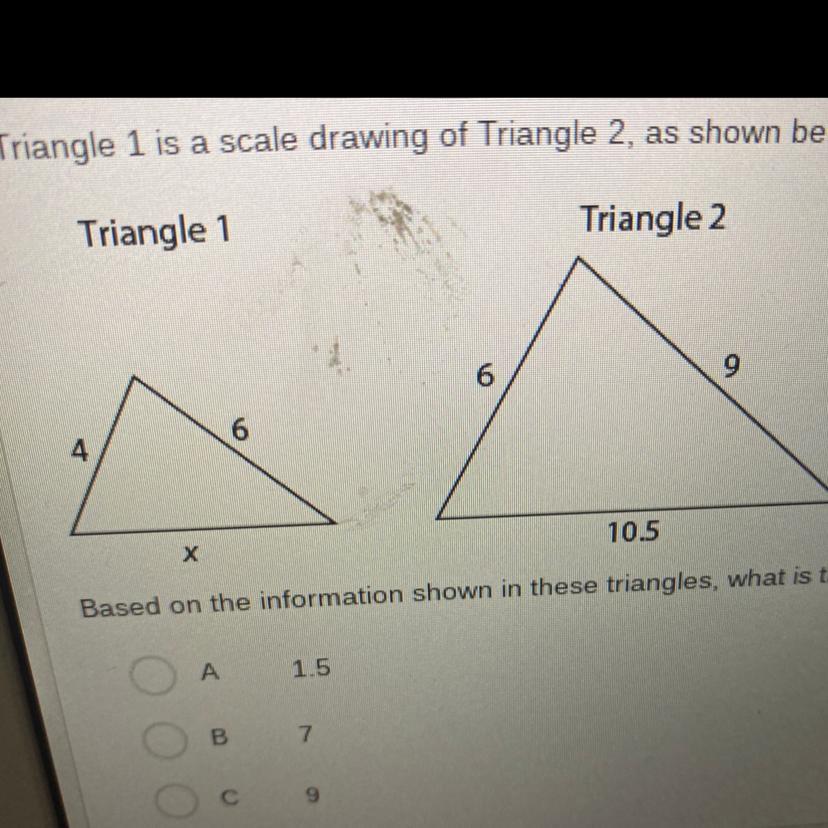
Answers
7
6 / 4 = 1.5 so that means 6 / 1.5 = 4
now that we have that, 10.5 / 1.5 = 7
Answer:
its 7.
Step-by-step explanation:
Please answer correctly !!!!!!!!!!!!!! Will mark brainliest !!!!!!!!!!!!!!!

Answers
Answer:
acute = 30,right angle = 90,obtuse = 135,line = 180
Plzzzzz urgenttttt❤️❤️❤️

Answers
D. 2322.50
Step-by-step explanation:
I hope it's right.
Write an inequality for the graph below

Answers
Answer:
y > -1/4x + 4
Step-by-step explanation:
First find the equation of the line itself, which is y = -1/4x + 4, then determine if graph shades above the line or below the line. If it shades above which is true in this case, it will be greater than. If it shades below which does not occur in this case, it will be less than. Because the line is dashed and not solid, it will just be greater than or less than.
Therefore y = -1/4x + 4 → y > -1/4x + 4 [Shades above the line, line is dashed].
add the following polynomial of x3+3xy-2×y2+y3,2×3-5x2y-3xy2-2y3
Answers
The addition of the polynomial \(x^{3}+3xy-2xy^{2} +y^{3}\) with \(2x^{3}-5x^{2} y-3xy^{2}-2y^{3}\) is \(3x^{3}+3xy-5x^{2} y-5xy^{2}-y^{3}\).
What is a polynomial?
⇒ A polynomial is an expression consisting of indeterminates and coefficients, that involves only the operations of addition, subtraction, multiplication, and non-negative integer exponentiation of variables.
⇒ In the addition of polynomials, the like terms are added while in subtraction, the like terms are subtracted.
Calculation;
We have been given two polynomial which we have to add \(x^{3}+3xy-2xy^{2} +y^{3}\) and \(2x^{3}-5x^{2} y-3xy^{2}-2y^{3}\)
The sign after addition or subtraction will always be of the variable having more value.
\((x^{3}+3xy-2xy^{2} +y^{3} )+(2x^{3}-5x^{2} y-3xy^{2}-2y^{3})\)
On adding like terms with each other
⇒ \((x^{3} +2x^{3})+ 3xy-5x^{2} y-(2xy^{2}+3xy^{2})+(y^{3}-2x^{3})\)
⇒ \(3x^{3}+3xy-5x^{2} y-5xy^{2}-y^{3}\)
Hence the addition of the polynomial\(x^{3}+3xy-2xy^{2} +y^{3}\) and \(2x^{3}-5x^{2} y-3xy^{2}-2y^{3}\) is \(3x^{3}+3xy-5x^{2} y-5xy^{2}-y^{3}\).
Learn more about polynomial here :
brainly.com/question/1487158
#SPJ9