2. Which of the following is the correct interpretation of confidence interval? (circle one)
a. If the same experimental process is done on many samples, with a given percentage certainty,
the population parameter will fall within a calculated range.
b. When many different processes are done on the same sample, with a given percentage certainty,
the population parameter will fall within a calculated range.
c. If the same experimental process is done on many samples, with a given percentage certainty,
each sample will determine its own calculated range with a given percentage certainty
3. In a certain study, a population parameter is predicted to be in the interval (42, 60) at a 95% confidence
level. What is a reasonable confidence interval if the confidence level is adjusted to 98%
Explain your answer.
Answers
Related Questions
For each pair of X and Y variables, decide which correlation coefficient to compute. Assume that the relationship between X and Y is linear. Phi Pearson r Spearman Point biserial o o X = whether a film's cast incudes an A-list movie star, and Y-the film's box office revenue. A high school senior ranks the colleges she has applied to in terms of their attractiveness to her. x - the college's tuition, and Y - the attractiveness rank the senior assigns to the college. X = whether a person slept with the lights on or off at night as an infant, and Y - whether the person is nearsighted as an adult. X = the average number of pages in a magazine, and Y = the magazine's subscription price.
Answers
The correlation coefficient chosen depends on the types of variables involved, and each coefficient is specifically designed for certain combinations of variables.
What is a Variable?
A variable is a quantity that can change in the context of a mathematical problem or experiment. We usually use one letter to represent a variable. The letters x, y, and z are common general symbols used for variables.
To determine which correlation coefficient to calculate for each pair of variables X and Y, we must consider the nature of the variables involved. Here is the corresponding correlation coefficient for each scenario you provided:
X = whether the film's cast includes film star A and Y = the film's box office receipts:
In this case, since both variables are binary (yes or no), the appropriate correlation coefficient to calculate is the point biserial correlation coefficient. This coefficient measures the strength and direction of the relationship between a binary variable (X) and a continuous variable (Y).
X = college tuition and Y = attractiveness rating assigned by a high school graduate:
Here, X represents a continuous variable (tuition), while Y represents an ordinal variable (attractiveness rank). You should use Spearman's rank correlation coefficient to determine the correlation between these variables. This coefficient evaluates a monotonic relationship between two variables, even if the relationship is not strictly linear.
X = whether the person slept at night with the lights on or off as an infant and Y = whether the person is myopic as an adult:
In this case, X is a binary variable (yes or no) and Y is also a binary variable. You can use the phi coefficient to assess the relationship between these variables. The phi coefficient is suitable for measuring the correlation between two binary variables.
X = the average number of pages in the magazine and Y = the price of a magazine subscription:
Here, X represents a continuous variable (number of pages) and Y represents another continuous variable (subscription price). For this scenario, the appropriate correlation coefficient to calculate is the Pearson correlation coefficient. This coefficient assesses the linear relationship between two continuous variables.
Note that the correlation coefficient chosen depends on the types of variables involved, and each coefficient is specifically designed for certain combinations of variables.
To learn more about Variable from the given link
https://brainly.in/question/48827794
#SPJ4
If (a^x a ^y) - a^z = a^m then express m in terms of x, y and z.
Answers
Answer:
m = x+y-z
Step-by-step explanation:
Given the expression.
(a^x a ^y) ÷ a^z = a^m
We are to express m in terms of x, y and z.
Using the multiplicative law of indices, the expression becomes:
a^{x+y} ÷ a^z = a^m
Applying the division rule in indices
a^{x+y} ÷ a^z = a^{x+y-z}
The equation becomes
a^{x+y-z} = a^m
Cancel out the base and equate the powers as shown:
x+y-z = m
Hence the expression of m in terms of x, y and z is m = x+y-z
Can someone help with this

Answers
Answer:
can you post the whole screen
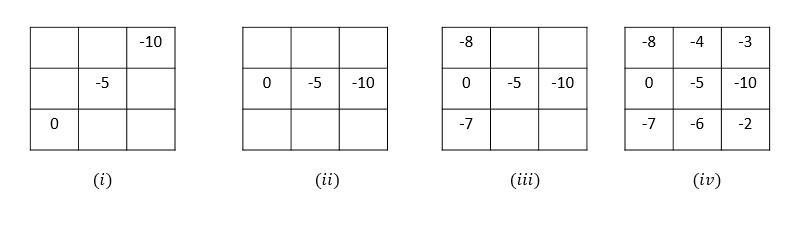
Lntegers 0, -2, -3, -4, -5, -6, -7, -8, and -10 to fill in a 3 x 3 magic square so that every row, column, and diagonal has the same sum. The sum must be -15.
Answers
The given numbers are 0, -2, -3, -4, -5, -6, -7, -8, and -10.
Sum of all the integers is -45.
There are 9 places in 3x3 magic square, so divide -45 by 9, we have -45/9=-5.
Put the number -5 at the center place in the magic square.
Now, take the integer having the largest magnitude, i.e -10.
There are two positions to place -10, one is diagonal positions and the other is non-diagonal positions and to make sum = -15, the other number with -5 and -10 must be 0 as shown in the figure (i) and (ii).
Now, the row and column having 0 must have -8 and -7 to make sum -15, which disregards the possibility of -10 at the diagonal place ( figure (i)). So, proceeds with the places in figure (ii), the possible places of -8 and -7 have been shown in figure (iii).
Now, as the sum of diagonals = -15, so place -3 and -2 at diagonal positions and also place the remaining numbers -4 and -6 to make the sum of numbers in columns and rows -15 as shown in figure (iv).
In a class of 25 students, some students play a sport, some play a musical instrument, some do both, some do neither. Complete the two-way table below. Due ASAP!

Answers
Does not do instrument and sport will be 2 (middle). Then you can go horizontol for does not play sport with the total being 7 (middle right) . 25 - 7 = 18 (top right). 18 - 16 = 2 (top left). 5 + 2 = 7(Bottom left)
Hope it helped because i cant really draw on it. :<
Two-way table for the given data is attached in the picture.
Two way table for the given data: Data given in each row will sum in the column 'total'. Data given in each column will sum in the last row.Last row → (Plays an instrument) + (does not play an instrument) = 25
Plays an instrument = 25 - 18 = 7
First column → Students play an instrument and plays a sport + Students play an instrument but don't play a sport = Column total
Students play an instrument and plays a sport + 5 = 7
Students play an instrument and plays a sport = 7 - 5 = 2
Column two → Students who do not play an instrument but play a sport + Students who do not play an instrument and do not play a sport = column total
16 + Students who do not play an instrument and do not play a sport = 18
Students who do not play an instrument and do not play a sport = 18 - 16
= 2
Second row → Students who play an instrument but do not play a sport + Student who neither play a sport nor play an instrument = Total of second row
Total of the second row = 5 + 2 = 7
First row → Students who play an instrument and play a sport + Students who do not play an instrument and play a sport = Total of first row
Total of the first row = 2 + 16 = 18
Therefore, two way table will be as shown in the picture attached.
Learn more about the two-way table here,
https://brainly.com/question/3921017?referrer=searchResults

A hunter shot 7 ducks. The hunter's dog recovered 5/7 of the ducks. How many ducks were recovered
Answers
Answer:
I think it would be 5/7
Explanation:
The question states "The hunter's dog recovered 5/7 of the ducks.", so I am guessing it would be 5/7
Hope this helps :)
Answer:
5 Ducks
Step-by-step explanation:
It is given that there were 7 ducks and 7 of those were shot in total. 7/7
It is also given that the dog retrieved 5/7 of them.
So, 7/7-5/7=2/7
2 ducks were not recovered, and 5 were
Hope I helped
The image below represents a 12 x 16 room with an 8 x 10 piece of linoleum centered in the room. The yellow and blue rectangles extend the length of their respective sides. Where these two rectangles overlap, there is a green rectangle. In the paragraph box, explain why the total colored area is 62 square feet.

Answers
The total area of the colored rectangles is 62 square feet
How to explain why the total colored area is 62 square feet?Given that: the room is 12 x 16 with an 8 x 10 piece of linoleum centered in the room
The shape will be treated as a composite rectangle. Thus, the room can be divided into smaller rectangles as shown in the image attached.
For the Yellow part:
Length(L) = 8 + 2 = 10 feet
width(W) = 3 feet
Area(A) = L × W
A = 10 × 3 = 30 square feet
For the Blue part:
Length(L) = 2 feet
Width(W) = 3 + 10 = 13feet
Area(A) = L × W
A = 13 × 2 = 26 square feet
For the Green part:
Length(L) = 2 feet
width(W) = 3 feet
Area(A) = L × W
A = 2 × 3 = 6 square feet
Total colored area = Area of Yellow + Area of Blue + Area of Green
Total colored area = 30 + 26 + 6 = 62 square feet
Therefore, the total colored area is 62 square feet
Learn more about area of composite rectangle on:
brainly.com/question/26992044
#SPJ1

pls help. i don't like math

Answers
Answer:
X = 5 3/8 (5 and 3 eighths)
Step-by-step explanation:
4/5x = 5 1/5 - 9/10
4/5x = 43/10
x=43/8
x= 5 3/8
Answer:
Exact Form: x=43/8
Decimal Form: 5.375
Mixed number form: x= 5 and 3/8
Step-by-step explanation: here is the steps

Condense logarithmic equation PLEASE!

Answers

ALREADY LATE PLS HELP!!!

Answers
Answer:
36 ounces
Step-by-step explanation:
9 x 4 = 36
134 x 0.01 what is it
Answers
how many trees are less than 12 m tall or at least 28 m tall?

Answers
The numbe of trees that are less than 12 m tall or atleast 28 m tall using from the histagram is 5
What is an Histagram?A histogram is a graph that shows the frequency of numerical data using rectangles.
In mathematics, "or" means addition.
From the question, to find the number of trees that are less than 12 m tall or atleast 28 m tall, we use the formula below.
Formula:
N = T+T'............... Equation 1Where:
N = The number of trees that are less than 12 m tall or atleast 28 m tallT = Number of trees that are less than 12 m tallT' = Number of trees that are atleast 28 m tallFrom the diagram,
T = 1+2 = 3 treesT' = 2 treesSubstitute these values into equation 1
N = 3+2N = 5 treesHence, the numbe of trees is 5.
Learn more about histagram here: https://brainly.com/question/251701
#SPJ2
A sample of bacteria taken from a river has an initial concentration of 2.1 million bacteria per milliliter and its concentration triples each week. (a) Find an exponential model that calculates the concentration after x weeks. (b) Estimate the concentration after 1.6 weeks. (a) B(x) = (Type an equation usingx as the variable.)
Answers
The exponential model that calculates the concentration of bacteria after x weeks can be represented by the equation B(x) = 2.1 million * (3^x), the concentration after 1.6 weeks would be approximately 14.87 million bacteria per milliliter.
This equation assumes that the concentration triples each week, starting from the initial concentration of 2.1 million bacteria per milliliter.
To estimate the concentration after 1.6 weeks, we can substitute x = 1.6 into the exponential model. B(1.6) = 2.1 million * (3^1.6) ≈ 14.87 million bacteria per milliliter. Therefore, after 1.6 weeks, the estimated concentration of bacteria in the river would be approximately 14.87 million bacteria per milliliter.
The exponential model B(x) = 2.1 million * (3^x) represents the concentration of bacteria after x weeks, where the concentration triples each week. By substituting x = 1.6 into the equation, we estimate that the concentration after 1.6 weeks would be approximately 14.87 million bacteria per milliliter.
Learn more about equation here:
https://brainly.com/question/29538993
#SPJ11
HELPPPP
Amanda buys a used car for $10,450. It depreciates in
value 11% each year. Write an equation to represent
how much the car is worth in n years.
Answers
Initial value is a term used in mathematics and other fields to refer to the starting value of a function or variable at the beginning of a given time period or process.
To represent how much the car is worth in n years, we need to use the following formula:
Value after n years = Initial value x (1 - depreciation rate)^n
In this case, the initial value of the car is $10,450 and the depreciation rate is 11% per year. So, we can substitute these values into the formula:
Value after n years = $10,450 x (1 - 0.11)^n
Simplifying this equation gives us:
Value after n years = $10,450 x 0.89^n
Therefore, if you want to find out how much the car is worth after a certain number of years, you can plug in the value of n into this equation and solve for the value.
I hope this helps! Let me know if you have any other questions.
To know more about Initial value visit:
https://brainly.com/question/13243199
#SPJ11
All students wrote the test with an average of 6 points. Exactly 60% of these students passed the test successfully. Those students who successfully passed the test received an average of 8 points. How many points were received on average by those students who did not pass the test successfully?
Answers
Answer:
The average points received by those students who did not pass the test successfully would be 4 points.
Step-by-step explanation:
Step 1: We know that all students wrote the test and received an average of 6 points.
Step 2: We also know that 60% of those students passed the test successfully and received an average of 8 points.
Step 3: This means that the remaining 40% of students did not pass the test successfully.
Step 4: Since the average points for all students was 6 points and the average points for those who passed the test was 8 points, the average points for those who did not pass the test would be 4 points.
HELP!!! WILL GIVE BRAINLEST AND POINTS!!! PLEASE SOLVE THESE TWO EQUATIONS!! -2(x + 4) = -16 x/3 + 5 = 10
Answers
Answer:
4, 15
Step-by-step explanation:
First of all, simplify the first equation. When you simplify, you get -2x-8 = -16, which you then add 8 to both sides. You get -2x = -8, so you divide both sides by -2 to get 4. In the second equation, you subtract 5 from both sides to get x/3= 5. Multiply both sides by 3 to get the value of x, and you'll get the equation of x=15, which is the answer.
write the additive and multiplicative imverse of -1/2 ?
Answers
Answer:
The additive inverse is \(\frac{1}{2}\), and the multiplicative inverse is -2.
Step-by-step explanation:
Hope this helped!
Find the sum of the digits in the product of: 1001x1001x1001
Answers
Answer:
1003003001
Step-by-step explanation:
1001x1001x1001=1003003001
Answer:
1,003,003,001
Step-by-step explanation:
\(1001^3=1,003,003,001\)
A mountain is in the shape of a cone whose height is about 3.8 kilometers and whose base radius is about 3 kilometers. Approximate the volume of the mountain in cubic kilometers.
The volume of the mountain is approximately cubic kilometers.
(Round to the nearest whole number as needed.)
Answers
Rounding to the nearest whole number, the approximate volume of the mountain is 36 cubic kilometers.
What is volume?Volume is a measure of the amount of space that a three-dimensional object occupies or contains. It is typically measured in cubic units, such as cubic meters, cubic centimeters, or cubic feet.
In the given question,
The volume of a cone can be calculated using the formula V = (1/3)πr²h, where r is the radius of the base, h is the height, and π is approximately 3.14.
Substituting the given values, we get:
V = (1/3) × 3.14 × 3² × 3.8
V ≈ 35.63
Rounding to the nearest whole number, the approximate volume of the mountain is 36 cubic kilometers.
To know more about volume, visit:https://brainly.com/question/30984370
#SPJ1
i need helppp
HELLPP!!!!!!!!!!!

Answers
√131 lies between 11 and 12.
What are whole numbers?The numbers that include natural numbers and zero are called whole numbers.
Given is the square root of 131.
We can write the square root of 131 as -
√131 = 11.45
We can write the whole numbers as -
11 < 11.45 < 12
Therefore, √131 lies between 11 and 12.
To solve more questions on numbers, visit the link below -
https://brainly.com/question/30034780
#SPJ1
Please I just need a simple explanation for this I will mark brainliest!!!!

Answers
Answer:
Step-by-step explanation:
Angle ACB = Angle YZX
In the reasoning SSS, u need 3 corresponding sides, and in this proof, u are given 2 sides and an angle, so technically the reason is SAS.
Angle ACB = Angle YZX
is the correct answer to the question
What are the 3 types of rigid transformations?
Answers
Three types of rigid transformations are Reflection, Rotation, and Translation. Rigid transformation, also called isometry.
A rigid transformation, also called isometry, is a transformation that doesn't change the size or shape of a geometric figure. The following are 3 types of rigid transformation:
1. Reflection
→ is the act of shifting an object's coordinates that flip it across a line without changing its shape or size. Horizontal (draw a figure to the left or right) or vertical (draw a figure to the up or down) reflections are possible. The result of reflection is a mirror image of the figure itself.
The figure is reflected across \(x-\) or \(y-\) axis, and then change \(x-\) or \(y-\) coordinate.
2. Rotation
→ is the non-modification of an object's size or shape by rotating it around an fixed point. A center of rotation is required to rotate an object. And the rotation did by using a degree.
The figure is rotated by a degree (ex: 90°), and then change \(x-\) or \(y-\) coordinate. Meanwhile, a point's center rotation stays at the same.
3. Translation
→ is sliding a figure in any direction without changing its size, shape, or orientation. Translation could be horizontal (make a figure left or right), or vertical reflections (make a figure up or down).
Vertical translation is shifting the graph along \(y-\) axis
Horizontal translation is shifting the graph along \(x-\) axis.
Here to learn more about Rigid Transformation:
https://brainly.com/question/1462871
#SPJ4
3)I NEED HELP FAST
Beth cuts a green apple into 6 slices. She ate 5 slices and gave 1 slice to her sister,
Eva. What fraction of the apple did Eva receive?
Answers
Answer:
uhhh ima guess 1/2
Step-by-step explanation:
because 6-5 is 1 and 1 is 1/2 in fractions ig
How would you describe the shape of the normal distribution?
Answers
The shape of the normal distribution is bell shape and it is also symmetrical from the left and right sides about the origins (mean).
What is a normal distribution?
A normal distribution is a function on some random variables, which represent the set of all those random variables in a symmetrical bell shape about the mean value.
It shows that the probability of occurrence of some data which is distributed over a function is more at or around the mean.
It is also known as probability distribution curve.
The normal distribution has two parameters:
MeanStandard deviationWhat is the shape of the normal distribution?
The normal distribution curve is at it's peak at the mean value. This shows that the probability of occurrence of the data or value is more concentrated or distributed about the mean. It is also symmetric about the mean. As we more further from the mean, we see that the normal distribution curve gradually decreases showing that the probability of occurrence of the data or the values decreases. The shape that this curve forms is like a bell-shaped. So the shape of normal distribution is bell shape.
Hence, the shape of the normal distribution is bell shape and it is also symmetrical from the left and right sides about the origins (mean).
Know more about "normal distribution" here: https://brainly.com/question/15103234
#SPJ4

solve for x

Answers
Answer:
x = 15.2
Step-by-step explanation:
you can use the Pythagorean Theorem on either half of the large triangle because you know one leg is 29/2 and the hypotenuse is 21
(29/2)² + x² = 21²
210.25 + x² = 441
x² = 230.75
x = \(\sqrt{230.75}\)
x = 15.2
A plane flying horizontally at an altitude of 1mi and a speed of 350mi/h passes directly over a radar station. Find the rate in mi/h at which the direct line distance from the plane to the radar station is increasing when it is 3mi away from the station. Let x= the horizontal distance from the plane to the radar station. Let y= the direct line distance from the plane to the radar station. a) What rate are you given? Express your answer in the form dx/dt or dy/dt= a number. Do not use parentheses around the dx/dt or the dy/dt. b) What rate are you trying to find? c) Write an equation relating x and y. Note: In order for WeBWorK to check your answer you will need to write your equation so that it has denominators. For example, an equation of the form 2/x=6/y should be entered as 6x=2y or y=3x or even y−3x=0. d) Use the chain rule to differentiate this equation and then solve for the unknown rate, leaving your answer in equation form. e) Substitute the given information into this equation and find the unknown rate. Express your answer in the form dx/dt or dy/dt=a number.
Answers
The rate at which the direct line distance from the plane to the radar station is increasing when it is 3 miles away from the station is approximately 332.11 mi/h.
a) The rate given is the speed of the plane, which is 350 mi/h. So we have dx/dt = 350 mi/h.
b) The rate we are trying to find is the rate at which the direct line distance from the plane to the radar station is increasing, which is dy/dt.
c) To write an equation relating x and y, we can use the Pythagorean theorem. The horizontal distance x is one side of a right triangle, the altitude 1 mi is the other side, and y is the hypotenuse. Therefore, we have the equation:
x² + 1² = y²
d) Differentiating the equation using the chain rule, we have:
2x(dx/dt) + 0 = 2y(dy/dt)
Simplifying, we get:
x(dx/dt) = y(dy/dt)
e) We are given that x = 3 mi and
dx/dt = 350 mi/h. Plugging these values into the equation from step d), we have:
(3 mi)(350 mi/h) = y(dy/dt)
Solving for dy/dt, we get:
dy/dt = (3 mi)(350 mi/h) / y
Since y is the direct line distance from the plane to the radar station, we can use the Pythagorean theorem to find its value when x = 3 mi:
x² + 1² = y²
(3 mi)² + 1² = y²
9 mi² + 1 mi² = y²
10 mi² = y²
y = √10 mi
Substituting this value into the equation for dy/dt, we have:
dy/dt = (3 mi)(350 mi/h) / (√10 mi)
dy/dt = 1050/√10 mi/h
Therefore, the rate at which the direct line distance from the plane to the radar station is increasing when it is 3 mi away from the station is approximately 332.11 mi/h.
To know more about differentiation, visit:
https://brainly.com/question/29972088
#SPJ11
A mixed bag of candy is 25% chocolate bars and 75% other filler candy. Of the chocolate bars, 50% of them contains caramel. Of the other filler candy, 10% of them contain caramel. What percent of candy contains caramel? *
Answers
Answer:
20% candy contains caramel.
Step-by-step explanation:
A bag of mixed candy has chocolate bars = 25%
and other filler candy = 75%
Let the 'c' represents the percentage of candy containing caramel in the bag of mixed candy.
Of the chocolate bars, percentage of candy containing caramel = 50% of 25%
Of the other filler candy, percentage of caramel candy = 10% of 75%
1c = 0.50(0.25) + 0.10(0.75)
= 0.125 + 0.075
= 0.2
By converting into percentage = 0.2 × 100 = 20%
20% candy contains caramel.
which of these collections of subsets are partitions of {1, 2, 3, 4, 5, 6}? a) {1, 2}, {2, 3, 4}, {4, 5, 6} b) {1}, {2, 3, 6}, {4}, {5} c) {2, 4, 6}, {1, 3, 5} d) {1, 4, 5}, {2, 6}
Answers
The collections of subsets that are partitions of {1, 2, 3, 4, 5, 6} are options (b) and (c).
Among the given options, collections (b) and (c) are partitions of the set {1, 2, 3, 4, 5, 6}. In option (b), the subsets {1}, {2, 3, 6}, {4}, and {5} form a partition since each element of the set belongs to exactly one subset.
Similarly, in option (c), the subsets {2, 4, 6} and {1, 3, 5} form a partition as each element is assigned to exactly one subset. On the other hand, options (a) and (d) do not satisfy the criteria of being a partition.
A partition of a set is a collection of subsets that satisfies two conditions: The subsets are non-empty. Every element in the original set belongs to exactly one subset in the collection. Let's analyze each option to determine if it is a partition of {1, 2, 3, 4, 5, 6}:
a) {1, 2}, {2, 3, 4}, {4, 5, 6}
This option does not form a partition since the element 2 belongs to both the subsets {1, 2} and {2, 3, 4}. So, option (a) is not a partition.
b) {1}, {2, 3, 6}, {4}, {5}
This option forms a partition. Each element belongs to exactly one subset, and the subsets are non-empty. So, option (b) is a partition.
c) {2, 4, 6}, {1, 3, 5}
This option forms a partition. Each element belongs to exactly one subset, and the subsets are non-empty. So, option (c) is a partition.
d) {1, 4, 5}, {2, 6}
This option does not form a partition since the elements 2 and 6 do not belong to any subset in this collection. So, option (d) is not a partition.
Therefore, the collections of subsets that are partitions of {1, 2, 3, 4, 5, 6} are options (b) and (c).
To know more about subsets click here
brainly.com/question/31739353
#SPJ11
Rafael deposits $2000 into an account that pays simple interest at an annual rate 6% of . He does not make any more deposits. He makes no withdrawals until the end of 5 years when he withdraws all the money.
Answers
After 5 years, Rafael will have $2600 in his account when he withdraws all the money.
To calculate the amount of money Rafael will have after 5 years, including the interest earned, we can use the formula for simple interest:
A = P(1 + rt),
where:
A is the final amount,
P is the principal amount ($2000),
r is the annual interest rate (6% or 0.06),
t is the time in years (5 years).
Plugging in the values, we have:
A = $2000(1 + 0.06 * 5) = $2000(1 + 0.30) = $2000(1.30) = $2600.
know more about simple interest here:
https://brainly.com/question/30964674
#SPJ11
Choose the correct slope of the line that passes through the points (−4, 8) and (−3, −6).
A. 0
B. 14
C. 7
d. -14
Answers
Answer:
The answer is option DStep-by-step explanation:
The slope of a line given two points can be found by using the formula
\(m = \frac{ y_2 - y _ 1}{x_ 2 - x_ 1} \)
where
(x1 , y1) and (x2 , y2) are the points
From the question the points are
(−4, 8) and (−3, −6)
The slope is
\(m = \frac{ - 6 - 8}{ - 3 + 4} = \frac{ - 14}{1} \)
We have the final answer as
- 14Hope this helps you