15 < -5x
Help I need it for khan academny
Answers
\(\huge \boxed{\sf x < -3} \\\\\\ \displaystyle \sf 15 < -5x \\\\ Divide\ each\ side\ by\ -5\ and\ switch\ the\ symbol. \\\\ \frac{15}{-5} > \frac{-5x}{-5} \\\\-3 > x\)
Related Questions
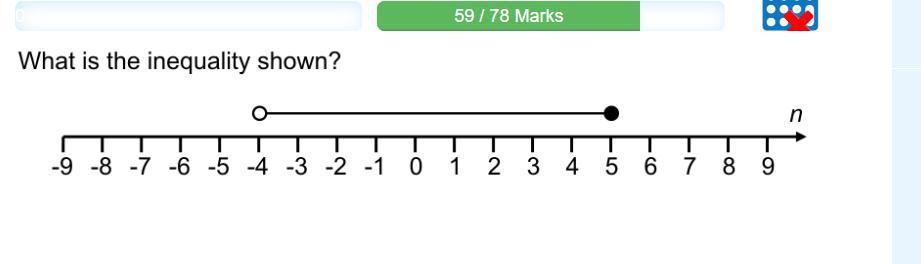
what is the inequality
Answers
Answer:-4<x<=5
Step-by-step explanation:
The white dot is above -4 and the filled in dot is above 5. Put that together plus the correct inequality signs and you get -4<x<=5
Answer: \(-4 < x\leq 5\)
Step-by-step explanation:
The inequality ends at 4 and it is colored white so x must be greater than -4 therefore the first expression is x > -4 or -4 < x.
The other side of the inequality ends at 5 and it's colored black so x is less than or equal to 5. Therefore the second expression is \(x\leq 5\).
if we merge the two equations together than we would get \(-4 < x\leq 5\).
I hope that helped you.
:)
The ratio of black bugs to blue bugs is 3 to5. If there are a total of 10 black bags, then how many black bags are there
Answers
that the answer is 18 bugs sorry pero yan ang tama
Step-by-step explanation:
please hearts me in brainly and give me a star
the measure of an exterior angle of a regular polygon is x, find the measure of one interior angle then find the number of sides
basically like 180 - x =
and then 180 ( n - 2 ) / n = 180 - x
all I need is to know what 180 - x is- if not I need to know what n is so I can solve the rest
Thankssssssss
Answers
Answer:
The polygon has 9sides with an interior angle measure of 140°
The exterior angle of a regular polygon=360°/n
40°=360°/n
n=360°/40°=9
So the polygon has 9 sides thus, a nonagon.
The measure of the interior angle=(n-2)180°/n
=(9-2)×180°/9=140°
Step-by-step explanation:
Have A Wonderful Day !!
Answer - was dis for free points? lel
in the figure, TU is tangent to the circle at point U. Use the figure to answer the question

Answers
Answer:
see explanation
Step-by-step explanation:
given a tangent and a secant drawn from an external point to the circle, then the square of the measure of the tangent is equal to the product of the secant's external part and the entire secant , that is
ST × RT = TU²
given RT = 13 and ST = 4 , then
TU² = 4 × 13 = 52 ( take square root of both sides )
TU = \(\sqrt{52}\) = 2\(\sqrt{13}\) ≈ 7.21 ( to 2 decimal places )
Step-by-step explanation:
intersecting secants theorem :
let's assume the second line would not be a tangent but a true secant with a second circle intersection point V, then
ST × RT = TU × TV
in other words : the product of the lengths of the short (external) segment and the full secant is the same for every secant line originating from the same point.
now we have the extreme case that U = V due to the tangent situation.
but the same principle applies. just TU = TV, and therefore
ST × RT = TU²
RT = TU²/ST
for the same reason and with the same approach, yes, we can calculate TU out of a given set of RT and ST :
TU² = ST × RT
TU = sqrt(ST × RT) = sqrt(4 × 13) = sqrt(52) = 2×sqrt(13) =
= 7.211102551...
ryan bought 4 2/3 pounds of apples for $0.75 per pound. how much did he pay for the apples
Answers
Answer:
$3.50
Step-by-step explanation:
4 2/3 x 0.75 = $3.50
Answer:$3.5
Step-by-step explanation:
The ratio of boys to girls at a school is 12 to 13. If 300 students attend the school, how many are boys?
144
277
156
25
Answer: 144
Answers
Answer:
144
Step-by-step explanation:
300 divided by 13
Write an equation of a line that passes through the point (-9,2) and is perpendicular to the line y=3x-12
A.y=-3x+12
B.y=(1/3)x-2
C.y=(-1/3)x-1
D.y=3x-1
Answers
Answer:
Step-by-step explanation:
perp. -1/3
y - 2 = -1/3(x + 9)
y - 2 = -1/3x - 3
y = -1/3x - 1
answer is C
consider the following random sample of income and education: income(y) education(x) 100 18 65 14 47 14 112 16 34 12 85 16 92 18 83 14 67 16 29 12 a. find sample means, variances, and standard deviations of x and y. b. find sample covariance, cov(y,x), and correlation corr(y,x). c. find cov(2y,3x), and correlation corr(2y,3x) d. find covariance of y and y and corr
Answers
The sample means are Mean(Y) = 61.4 and Mean(X) = 15, the sample variances are Variance(Y) ≈ 1124.89 and Variance(X) ≈ 2.67, the sample standard deviations are Standard deviation(Y) ≈ 33.56 and Standard deviation(X) ≈ 1.63, the sample covariance is Covariance(X, Y) ≈ -131.69, and the sample correlation is Correlation(X, Y) ≈ -0.77.
a. To find the sample means, variances, and standard deviation, we can use the following formulas:
Sample mean of income (Y):
Mean(Y) = (100 + 65 + 47 + 112 + 34 + 85 + 92 + 83 + 67 + 29) / 10 = 614 / 10 = 61.4
Sample mean of education (X):
Mean(X) = (18 + 14 + 14 + 16 + 12 + 16 + 18 + 14 + 16 + 12) / 10 = 150 / 10 = 15
Sample variance of income (Y):
Variance(Y) = [(100 - 61.4)^2 + (65 - 61.4)^2 + (47 - 61.4)^2 + (112 - 61.4)^2 + (34 - 61.4)^2 + (85 - 61.4)^2 + (92 - 61.4)^2 + (83 - 61.4)^2 + (67 - 61.4)^2 + (29 - 61.4)^2] / 9 ≈ 1124.89
Sample variance of education (X):
Variance(X) = [(18 - 15)^2 + (14 - 15)^2 + (14 - 15)^2 + (16 - 15)^2 + (12 - 15)^2 + (16 - 15)^2 + (18 - 15)^2 + (14 - 15)^2 + (16 - 15)^2 + (12 - 15)^2] / 9 ≈ 2.67
Sample standard deviation of income (Y):
Standard deviation(Y) = √Variance(Y) ≈ √1124.89 ≈ 33.56
Sample standard deviation of education (X):
Standard deviation(X) = √Variance(X) ≈ √2.67 ≈ 1.63
b. To find the sample covariance and correlation, we can use the following formulas:
Sample covariance:
Covariance(X, Y) = [(18 - 15)(100 - 61.4) + (14 - 15)(65 - 61.4) + (14 - 15)(47 - 61.4) + (16 - 15)(112 - 61.4) + (12 - 15)(34 - 61.4) + (16 - 15)(85 - 61.4) + (18 - 15)(92 - 61.4) + (14 - 15)(83 - 61.4) + (16 - 15)(67 - 61.4) + (12 - 15)(29 - 61.4)] / 9 ≈ -131.69
Sample correlation:
Correlation(X, Y) = Covariance(X, Y) / (Standard deviation(X) * Standard deviation(Y)) ≈ -131.69 / (1.63 * 33.56) ≈ -0.77
Learn more about standard deviations here:
https://brainly.com/question/12402189
#SPJ11
Correct question-
Consider the following random sample of income and education: Income(Y) Education(X) 100 18 65 14 47 14 112 16 34 12 85 16 92 18 83 14 67 16 29 12 a. Find sample means, variances and standard deviation. b. Find sample covariance and correlation.
If 2(4x+3)-12=3x-6 then what value of x makes the equation true
Answers
The value of x that makes the equation 2(4x + 3) - 12 = 3x - 6 true is 0.
An equation is a mathematical statement that asserts the equality of two expressions. It consists of two expressions separated by an equal sign (=). The expressions can contain variables, numbers, and mathematical operations, such as addition, subtraction, multiplication, and division.
To make the equation 2(4x + 3) - 12 = 3x - 6 true, find the value of x that will make the value of the right side equal to the value of the left side.
First, expand the equation.
8x + 6 - 12 = 3x - 6
Isolate the variable x in one side, the constants on the other.
8x - 3x = 12 - 6 - 6
5x = 0
Divide both sides by 5.
x = 0
Hence, the value of x is 0.
Checking:
2(4x + 3) - 12 = 3x - 6
2[4(0) + 3] - 12 = 3(0) - 6
-6 = -6
Learn more about equation here: https://brainly.com/question/2972832
#SPJ4
NEED HELP ASAP PLEASS AND THANK YOU

Answers
Answer:
Using points ( 2 , - 4) and ( 0 , 2)
Slope = 2+4/0-2 = 6/-2 = - 3
Since the lines are parallel their slope will be the same
So the slope of the line parallel to the one in the picture is - 3
That's option A.
Hope this helps.
Answer:
i believe its: -1/3
Step-by-step explanation:
if the line is parallel to the original line, the slope should be the same, and the slope of the original line is - 1/3. the slope is negative because the line is heading downwards, or in a negative direction. hope this helped!!
What is 6r-6r^2 simplified?

Answers
Answer:
I would just rewrite it as -6r^2 + 6r
the objective function for a linear optimization problem is: max 3x 2y, with one of the constraints being x and y both only take the values 0, 1. also x and y are the only decision variables. this is an example of a
Answers
This is an example of a binary integer linear programming problem, where the decision variables x and y can only take on the values of 0 or 1.
The objective function for a linear optimization problem is the mathematical expression that needs to be maximized or minimized. In the given example, the objective function is "max 3x + 2y."
The objective function represents the quantity or value that we want to optimize, in this case, maximize.
The coefficients of the decision variables x and y (3 and 2, respectively) determine the contribution of each variable to the objective value.
The constraint that states "x and y both only take the values 0, 1" indicates that x and y are binary decision variables. In other words, they can only take the values of 0 or 1.
Considering the constraints and the objective function, this example falls under the category of a binary linear optimization problem, where the decision variables are restricted to binary values.
The goal is to find the values of x and y (either 0 or 1) that maximize the objective function.
Therefore, the answer is: a) an example of a binary linear optimization problem.
To know more about binary integers refer here:
https://brainly.com/question/31560694#
#SPJ11
When Meghan's cat doubles his current weight, w, he will weigh 10 pounds. Move values into the boxes to create an equation that represents this scenario?
Answers
Answer:
The current weight of the cat is w, and we know that when the cat doubles the weight, it will weight 10 pounds
Then we can write the equation
2*w = 10 pounds
Now we can solve this for w, we must divide by 2 in both sides of the equality.
2*w/2 = 10/2 pounds
w = 5 pounds
The actual weight of the cat is 5 pounds.
for each number x in a finite field there is a number y such x y=0 (in the finite field). true false
Answers
The answer is False. In a finite field, for each non-zero number x, there exists a multiplicative inverse y such that x*y = 1, not 0. The only number that would satisfy x*y = 0 in a finite field is when either x or y is 0.
True. In a finite field, every non-zero element has a multiplicative inverse, meaning that there exists a number y such that x*y = 1. Therefore, if we multiply both sides by 0, we get x*(y*0) = 0, which simplifies to x*0 = 0. Therefore, for each number x in a finite field, there is a number y such that x*y = 0.
Multiplying an even number equals dividing by its difference and vice versa. For example, dividing by 4/5 (or 0.8) will give the same result as dividing by 5/4 (or 1.25). That is, multiplying a number by its inverse gives the same number (because the product and difference of a number are 1.
The term reciprocal is used to describe two numbers whose product is 1, at least in the third edition of the Encyclopedia Britannica (1797); In his 1570 translation of Euclid's Elements, he mutually defined inversely proportional geometric quantities.
In the multiplicative inverse, the required product is usually removed and then understood by default (as opposed to the additive inverse). Different variables can mean different numbers and numbers. In these cases, it will appear as
ab ≠ ba; then "reverse" usually means that an element is both left and right reversed.
Learn more about the multiplicative inverse:
brainly.com/question/13715269
#SPJ11
PLEASE SOMEONE HELP! Thanksss

Answers
Answer:
Ф=144
Ф =s/r ( Ф is the central angle,s is the arc length, r is the radius)
find r:
radius =circumference/2π=1/2π=0.16
Ф=(2/5) /(1/2π)=4π/5=144 degree (π=180)
Ф in degrees: 144 degrees
use Vieta's theorem to solve the problem:
the difference of the two solution of x^2+19x+c=0 is 15. find c
Answers
The difference between the two solutions of the quadratic equation ax² + bx + c = 0 can be found using Vieta's theorem. Let the roots of the quadratic equation ax² + bx + c = 0 be α and β. Therefore, α + β = -b/a and αβ = c/a.In order to solve the problem x² + 19x + c = 0, where the difference of the two solutions is 15, we can use Vieta's theorem.The roots of the quadratic equation are α and β.α - β = 15, where α is the larger root and β is the smaller root.Using Vieta's theorem, we haveα + β = -19/cand αβ = cWe will use α - β = 15 and α + β = -19/c to solve for α and βα + β = -19/cα - β = 15Solving for α and β:α = -19/2c - 15/2β = -19/2c + 15/2αβ = -c/2(19/2c + 15/2)(-19/2c + 15/2) = -c/2We have(19/2c + 15/2) x (19/2c - 15/2) = c/2(361/4c² - 225/4) = c/2Simplifying the expression, we get,361/4c² - 225/4 = c/2Multiplying by 4 on both sides, we have,361/c² - 225 = 2cThe quadratic equation obtained can be solved by simplifying and getting the factors.
Using the Vieta's theorem, if the difference of the two solution of x^2+19x+c=0 is 15. c is 34.
What is the value of c?Vieta's theorem states that for a quadratic equation of the form ax^2 + bx + c = 0
Sum of the roots= -b/a
Product of the roots = c/a
Let's denote the two solutions as x1 and x2.
Based on the given information:
x1 - x2 = 15
Using Vieta's theorem
Sum of the roots = -b/a
Coefficient of x = 19
so:
x1 + x2 = -19
The coefficient of x² is 1
x1 * x² = c/1 = c
Rearrange
x1 = -19 - x2
Substitute this into the equation x1 - x2 = 15
(-19 - x2) - x2 = 15
-19 - 2x2 = 15
-2x2 = 34
x2 = -17
Substitute the value of x2 into x1 + x2 = -19
x1 - 17 = -19
x1 = -2
The value of c using Vieta's theorem:
c = x1 * x2 = (-2) * (-17) = 34
Therefore the value of c is 34.
Learn more about Vieta's theorem here:https://brainly.com/question/26260657
#SPJ4
Using the Change of Base Formula, What is the solution to the equation 2^x=y.
Round to the nearest thousandth.

Answers
In triangle ABC, if ∠A = 120°, a = 8, and b = 3, then ∠B =
Answers
Answer:
Step-by-step explanation:
Use the Law of Sines here:
\(\frac{sin120}{8} =\frac{sinB}{3}\) and cross multiply to get
8sinB = 3sin120 and solve for B:
\(sinB=\frac{3sin120}{8}\) and
sinB = .3247595264
Now hit the 2nd button and then sin to get
\(sin^{-1}(\)
on your display. After that open parenthesis, enter that decimal and hit enter to get that angle B = 18.95 which you can round to howeve many places you need.
Write an equation in slope-intercept from of the line that passes through (-2, 5) and (-4, -5)
Answers
Answer:
y = 5x + 15
Step-by-step explanation:
The formula for slope is [ y2-y1/x2-x1 ].
-5-5/-4-(-2)
-10/-2
5
Find the y-intercept using slope intercept form, slope, and one point.
5 = 5(-2) + b
5 = -10 + b
15 = b
Input all the data we solved for back into the expression.
y = 5x + 15
Best of Luck!
PLEASE HELP!!! 30+ POINTS
Use the following data to construct a frequency table and calculate the mean, mode, and median.

Answers
Answer:
A measure of average is a value that is typical for a set of figures. Finding the average helps you to draw conclusions from data. The main types are mean, median and mode. Data is also often grouped.
Step-by-step explanation:
To find the mean add all the ages together and divide by the total number of children.
If you type all those ages into a calculator it is easy to make an error.
When eliminating a loop-carried dependency that adds a constant, the closed-form direct solution will likely contain a multiplication. true or false
Answers
The statement "When eliminating a loop-carried dependency that adds a constant, the closed-form direct solution will likely contain a multiplication" is true because eliminating a loop-carried dependency that adds a constant simplifies the equation, but to obtain a closed-form direct solution, we need to express the result as a function of the current iteration's variables only
When eliminating a loop-carried dependency that adds a constant, the closed-form direct solution will likely contain a multiplication. This is because the loop-carried dependency adds a constant to the result of the previous iteration, which means that the current iteration's result is a function of both the current iteration's variables and the previous iteration's result.
By eliminating this dependency, we remove the need to use the previous iteration's result, which simplifies the equation. However, to obtain a closed-form direct solution, we need to express the result as a function of the current iteration's variables only, which often involves a multiplication. This is because multiplication is a fundamental mathematical operation that allows us to combine variables in a way that preserves their individual values.
Learn more about multiplication here
brainly.com/question/23269091
#SPJ4
True. When eliminating a loop-carried dependency that adds a constant, the closed-form direct solution will likely contain a multiplication. This is because the loop-carried dependency is typically expressed as an addition, and removing it would result in a product of the loop index and the constant.
when eliminating a loop-carried dependency that adds a constant, the closed-form direct solution will likely contain a multiplication. This is because the process often involves applying mathematical transformations that result in multiplications to simplify the loop and eliminate dependencies.
learn more about loop-carried dependency
https://brainly.com/question/31563150
#SPJ11
Consider the following counter-espionage puzzle to find whether there is a spy among n guests at a party. Every spy knows everyone else’s name but nobody will know theirs. Fortunately, if you ask any person at this event the name of any other person (other than yourself), they’ll tell you honestly whether they know. The non-spies will do so because they’re good, honest people, and the spy will do so because they want to seem like they fit in. So all you need to do is ask every pair at the party whether each knows the other’s name, right? Here’s the problem. If the spy happens to notice you doing this, they’ll get spooked and leave. You’ll need to ask as few questions as possible. Describe a protocol for finding a spy that: 1. Finds the spy if there is one. 2. Uses 3(n − 1) or fewer questions of the form "do you know that person’s name?" Your protocol should be recursive. Prove by induction on n that your protocol satisfies the two properties above. [Hint: By asking a single "what’s their name" question, you can always eliminate one person as a potential spy. You just need to figure out what to do after that...]
Answers
Total Questions = 3(n/2 - 1) + n/2 = 3n/2 - 3/2 + n/2 = 2n - 3/2. The recursive protocol guarantees that the spy can be found if there is one (Property 1) and uses 3(n - 1) or fewer questions (Property 2) for any number of guests n, as proven by induction.
Using a recursive protocol, we can follow these steps to solve the counter-espionage puzzle and locate the spy among the n partygoers:
Case in Point (n = 2):
Ask A and B, any two guests, if they know each other's names.
B is not the spy if A says "Yes." B is the spies otherwise.
Case Recursive (n > 2):
With roughly equal numbers of guests, divide the n guests into two groups, A and B.
Apply the protocol one group at a time to each group recursively.
Assume that one or both of the spies in group A and group B are identified by the recursive calls.
Now, we have to figure out which group has the spy or whether there is a spy between the two groups.
Consolidating the Findings:
Ask one guest from group A and one guest from group B if they know each other's names for each pair of guests.
The spy is part of the larger group if at least one pair answers "Yes" while the other responds "No."
There is no spying between the two groups if each pair in either group responds with either "Yes" or "No." In this instance, the group that was identified as having a spy during the recursive calls must contain the spy.
Final Outcome:
Divide the larger group into two subgroups and recursively apply the protocol if there is a spy in that group.
Keep going in this recursive manner until either a spy is found or it is determined that no guests have a spy.
We can use induction on n to demonstrate the efficiency and effectiveness of the protocol:
Case in Point (n = 2):
The spy is correctly identified among two guests by the protocol. It only asks one question, which is the bare minimum.
Step Inductive:
Consider the case of (n + 1) guests, assuming that the protocol functions properly for n guests.
Divide the guests (n + 1) into two groups with approximately n/2 members each. This can be accomplished by selecting n/2 guests at random from one group and distributing the remaining guests to the other.
Apply the protocol one group at a time to each group recursively. Using a maximum of 3(n/2 - 1) questions per group, this correctly identifies any spies within each group, according to the induction hypothesis.
Asking each pair of guests, one from each group, if they know each other's names brings the results together. This calls for n/2 inquiries.
The spy is part of the larger group if at least one pair responds incorrectly (one says "Yes" and the other says "No"). The larger group only has (n + 1)/2 guests in this instance.
During the recursive calls, the spy must be in the group identified as having a spy if all pairs respond with the same answer (either both "Yes" or "No"). There are maximum n guests in this group.
As a result, in the worst-case scenario, the number of questions that are asked are as follows:
The total number of questions is 3(n/2 - 1), plus n = 3n/2 - 3/2, plus n = 2n - 3/2.
As a result, the protocol ensures that the spy can be located if there is one (Property 1) and employs three questions (n - 1) or fewer (Property 2) for any number of guests n, as demonstrated by induction.
To know more about Property, visit
brainly.com/question/2807928
#SPJ11
9: Find sinθ if cosθ=4/5 is in the first quadrant.
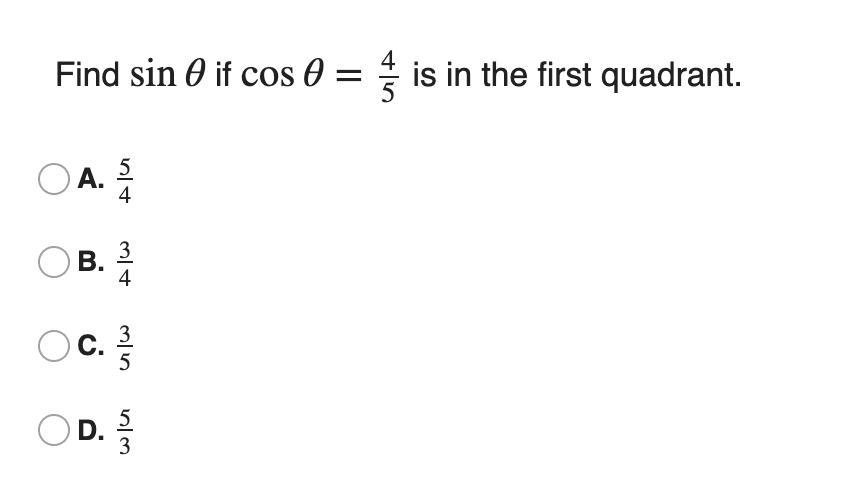
Answers
Answer: We have to find the sin(theta) provided the cos(theta) function, the visualization of the problem is as follows:
\(cos(\theta)=\frac{4}{5}\)The diagram visualization is:
Therefore the x is:
\(x=\sqrt{5^2-4^2}=3\)Therefore the answer is:
\(sin(\theta)=\frac{3}{5}\)The answer is Option(C).

Find series solution for the following differential equation.
Show ALL work and explain EACH step.
yll+2xy + 2y = 0
Answers
The series solution of the given differential equation is y(x) = 0.
Given Differential Equation: y'' + 2xy' + 2y = 0
We need to find the series solution for the given differential equation. For that, we can assume that the solution can be expressed in terms of the infinite power series which can be written as:
y(x) = a0 + a1x + a2x² + a3x³ + ... + anx^n + ...
where a0, a1, a2, ... , an, ... are the constants to be determined and x is the variable.
Now, let's differentiate y(x) with respect to x once and twice as shown below:
y'(x) = a1 + 2a2x + 3a3x² + ... + nanxn-1 + ...
y''(x) = 2a2 + 3.2a3x + 4.3a4x² + ... + n(n-1)anxn-2 + ...
Now, substitute the values of y(x), y'(x), and y''(x) in the given differential equation:
y'' + 2xy' + 2y = 0
2a2 + 3.2a3x + 4.3a
4x² + ... + n(n-1)anxn-2 + ... + 2x[a1 + 2a2x + 3a3x² + ... + nanxn-1 + ... ] + 2[a0 + a1x + a2x² + ... + anx^n + ...] = 0
Now, we will group the terms together by their powers of x, as shown below:
x⁰ terms: 2a0 = 0
⇒ a0 = 0
x¹ terms: 2a1 + 2a0 = 0
⇒ a1 = 0
x² terms: 2a2 + 2a1 + 4a0 = 0
⇒ a2 = - a0 - a1
= 0
x³ terms: 2a3 + 6a2 + 3.2a1 = 0
⇒ a3 = - 3a2/2 - a1/2
= 0
x⁴ terms: 2a4 + 12a3 + 4.3a2 = 0
⇒ a4 = - 6a3/4 - 3a2/4
= 0
x⁵ terms: 2a5 + 20a4 + 5.4a3 = 0
⇒ a5 = - 10a4/5 - 2a3/5
= 0
Therefore, the general solution of the given differential equation is:
y(x) = a0 + a1x + a2x² + a3x³ + ... + anx^n + ...
y(x) = 0 + 0x + 0x² + 0x³ + ... + 0xn + ...
y(x) = 0
Know more about the infinite power series
https://brainly.com/question/23612301
#SPJ11
What are the first five multiples of 12? Type the multiples in increasing order.
Answers
Answer:12, 24, 36, 48, 60
Answer:
12 (12*1), 24 (12*2), 36 (12*3), 48 (12*4), and 60 (12*5) (if 12 doesn't count, 72 is 12*6)
Find an exact simplified solution to the equation below so that 0 < θ < π/2.
1 = √(3) tan(2θ)
Θ=?
Answers
The simplified solution to the equation 1 = √(3) tan(2θ) where 0 < θ < π/2 is θ = π/12.
How can we find the exact simplified solution to the equation?To find the solution, we start by isolating the tangent term by dividing both sides of the equation by √(3). This gives us tan(2θ) = 1/√(3). We know that for 0 < θ < π/2, the tangent function is positive, and we are looking for the value of θ that satisfies this condition.
Using the inverse tangent function, we take the arctan of both sides to find the angle whose tangent is 1/√(3). The exact simplified solution is θ = π/12.
Learn more about: Inverse tangent function
brainly.com/question/31149456
#SPJ11
Shea and Chris drive to work. Shea drives 30 miles in 1.25 hours.Chris drives 62 km in 1 hour 15 min.Work out the difference between their average speeds in km/h.1 mile = 1.6 kmMy homework website says the answer is 11.2 I just don't understand how?? I got 15.5
Answers
The difference between their average speeds in km/h is 11.2. Your calculation of 15.5 may have been due to a conversion error.
To find the average speed, we divide the total distance traveled by the total time taken.
Shea drove 30 miles in 1.25 hours. To convert miles to kilometers, we multiply by the conversion factor 1.6 (since 1 mile = 1.6 km). So, Shea drove 30 * 1.6 = 48 km in 1.25 hours. Her average speed is 48 km / 1.25 hours = 38.4 km/h.
Chris drove 62 km in 1 hour 15 minutes. To convert minutes to hours, we divide by 60 (since there are 60 minutes in an hour). So, Chris drove 62 km in 1.25 hours. His average speed is 62 km / 1.25 hours = 49.6 km/h.
The difference between their average speeds is 49.6 km/h - 38.4 km/h = 11.2 km/h.
Therefore, the correct difference between their average speeds is indeed 11.2 km/h, not 15.5 km/h.
To learn more about convert miles click here
brainly.com/question/30764576
#SPJ11
Does a fluid obeying the clausius equation of state have a vapor-liquid transition? And why?
Answers
No, a fluid obeying the clausius equation of state have a vapor-liquid transition
This is because a straight line does not exist between a liquid's temperature and its vapour pressure.
What is the Clausius equation of state?The Clausius Clapeyron equation is described as a way of describing a known discontinuous phase transformation that exists between two phases of matter of a single constituent.
This equation was named after Rudolf Clausius and Benoît Paul Émile Clapeyron.
It also states that a straight line does not exist between a liquid's temperature and its vapour pressure.
The equation also helps us to estimate the vapor pressure at another temperature.
Learn more about clausius equation at: https://brainly.com/question/29414397
#SPJ1
Jill brought a pound of strawberries for 4.00 . what is the price,in dollars , per ounce of strawberries
Answers
Answer:
The price of per ounce of strawberries is $ 0.25.
Step-by-step explanation:
Pounds to ounce conversion:
As we know that,
One pound = 16 Ounce
Since, Jill bought a pound of strawberries for $4
It means that,
Price of 16 Ounces of strawberries = $ 4
So taht, Price of one ounce of strawberries
Hence, the price of per ounce of strawberries is $ 0.25.
Answer:
0.25
Step-by-step explanation:
16 ounces = 1 pound
4.00 / 16 = 0.25
NEED HELP ASAP PLS ILL MARK YOU BRAINLIEST IF ITS RIGHT

Answers
Answer:
The top table shows the sample space for two spins of this spinner.