10 x 10 - 4 divided by 7
Answers
Answer:
13.7142857143
Step-by-step explanation:
If you need to round then do so, or i will comment the rounded version if needed.
Related Questions
4p+6qp wdhwaudwhduwhdw
Answers
Answer:
10p
Step-by-step explanation:
Need help.
plz show steps

Answers
Answer:
-4
Step-by-step explanation:

Let f(x) = (3x + 9. Find f-'(x).=Vf-'(x) =help (formulas)

Answers
Given the function:
\(f\mleft(x\mright)=\sqrt{3x+9}\)You can find the Inverse Function by following the steps shown below:
1. Rewrite the function using:
\(f(x)=y\)Then:
\(y=\sqrt{3x+9}\)2. Solve for "x":
- Square both sides of the equation, in order to undo the effect of the square root on the right side:
\(\begin{gathered} (y)^2=(\sqrt[]{3x+9})^2 \\ y^2=3x+9 \end{gathered}\)- Apply the Subtraction Property of Equality by subtraction 9 from both sides of the equation:
\(\begin{gathered} y^2-(9)=3x+9-(9) \\ \\ y^2-9=3x \end{gathered}\)- Apply the Division Property of Equality by dividing both sides of the equation by 3:
\(\begin{gathered} \frac{y^2-9}{3}=\frac{3x}{3} \\ \\ \frac{y^2-9}{3}=x \\ \\ x=\frac{y^2-9}{3} \end{gathered}\)3. Swap the variables:
\(y=\frac{x^2-9}{3}\)4. Replace the variable "y" with:
\(y=f^{-1}(x)\)Then, you get:
\(f^{-1}(x)=\frac{x^2-9}{3}\)Hence, the answer is:
\(f^{-1}(x)=\frac{x^2-9}{3}\)Tomas has a garden with a length of 2. 45 meters and a width of 5/8 meters. Use benchmarks to estimate the area and perimeter of the garden?
Answers
The estimated perimeter of Tomas's garden is approximately 6.2 meters.
To estimate the area of Tomas's garden, we can round the length to 2.5 meters and the width to 0.6 meters. Then we can use the formula for the area of a rectangle:
Area = length x width
Area ≈ 2.5 meters x 0.6 meters
Area ≈ 1.5 square meters
So the estimated area of Tomas's garden is approximately 1.5 square meters.
To estimate the perimeter of the garden, we can add up the lengths of all four sides.
Perimeter ≈ 2.5 meters + 0.6 meters + 2.5 meters + 0.6 meters
Perimeter ≈ 6.2 meters
So the estimated perimeter of Tomas's garden is approximately 6.2 meters.
Learn more about perimeter from
https://brainly.com/question/397857
#SPJ11
In the expression 2x + y - 4, the coefficient of y is...
Answers
Answer:
1
Step-by-step explanation:
If a term does not have a written coefficient, then the coefficient is one.
This is because 1(y) = y
Answer:
1
Step-by-step explanation:
there is an "understood" 1 as the coefficient of any blank variable
but it is useless to write since anything times 1 is just the same number ..... (i.e: y *1= y...same as 5 * 1= 5)
plz help me!! Polynomial Long Division (Level 2)
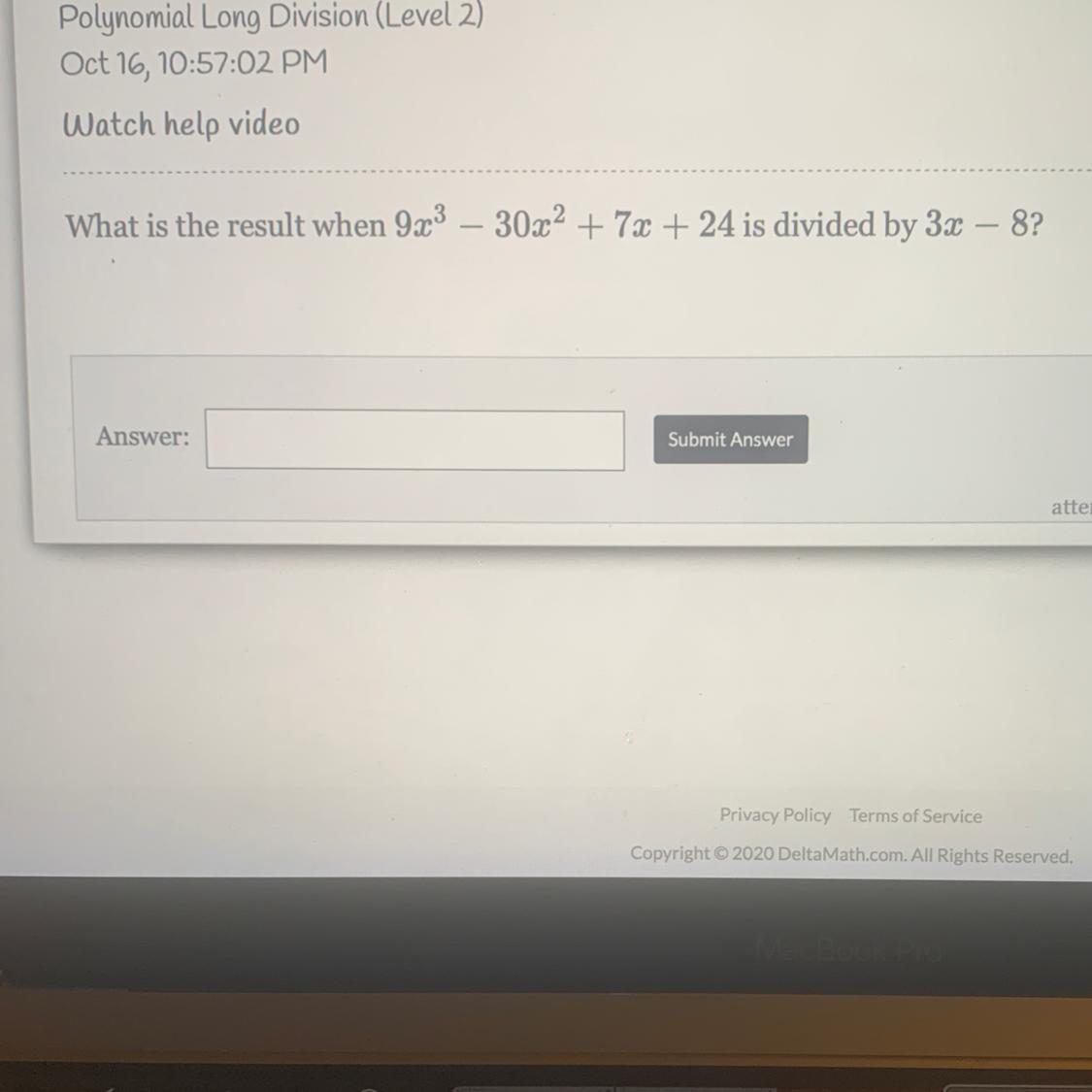
Answers
Explanation:
I got a picture to show

#73 will give brainliest to best answer!

Answers
Answer:
y=x^2+6
Step-by-step explanation: Look at the vertex (0,6). We know the equation is quadratic so we know x^2. We know in the slope-interpect form equation the y-intercept is the term after the slope. The same applies in this equation. So that means the y intercept is 6 because y is 6 in the coordinate (0,6). We know the slope x^2. We need to plug that into the slope-intercept form equation.
The equation will be y=x^2+6.
Answer:
\(y = x^2 + 6\)
Step-by-step explanation:
Vertex form for a parabola is \(y = a(x-h)^2 + k\) where the vertex is \((h,k)\). Now for a vertex of (0,6), we can simply plug those values in for h and k: \(y = x^2 + 6\).
Hope this helps!! :)
What’s the answer to this

Answers
Answer:
v=9
Step-by-step explanation:
50 + x =180
x=130
130+(6v-4)= 180 (subtract 126 from each side)
6v=54 (divide by 6)
v=9
Solve for x.
X=
x +19 7x +9
Answers
Step-by-step explanation:
X+7x=9-19
8x=-10
X=-10÷8
X=1.25
About how many gallons of grape juice are shown in the picture?
A. 15
B.10
C.4
D.3

Answers
find the value of f(4)

Answers
Answer:
5
Step-by-step explanation:
For this question, look for the y value when x=4. The y-value when x=4 is 5.
Two adjacent sides AB and BC of a parallelogram ABCD are in the ratio 5 : 3 . If the perimeter is 320 cm , what is the length of AB and BC
Answers
The length of AB is 100 cm and the length of BC is 60 cm.
Let's assume the length of AB is 5x and the length of BC is 3x, where x is a common factor.
In a parallelogram, opposite sides are equal in length. Therefore, the length of AD is also 5x, and the length of CD is 3x.
The perimeter of a parallelogram is the sum of the lengths of all its sides. Given that the perimeter is 320 cm, we can set up the equation:
AB + BC + CD + AD = 320
(5x) + (3x) + (3x) + (5x) = 320
16x = 320
Dividing both sides by 16:
x = 320 / 16
x = 20
Now we can find the lengths of AB and BC:
AB = 5x = 5 * 20 = 100 cm
BC = 3x = 3 * 20 = 60 cm
Therefore, the length of AB is 100 cm and the length of BC is 60 cm.
For such more questions on length of AB
https://brainly.com/question/24308330
#SPJ8
How many square inches of cloth are cut from the square (n = 3.14) if it’s 38inches
Answers
The number of square inches of cloth cut from the square will be 1,017.36 square inches. Then the correct option is A.
What is the area of the circle?It is the close curve of an equidistant point drawn from the center. The radius of a circle is the distance between the center and the circumference.
Let r be the radius of the circle. Then the area of the circle will be
A = πr² square units
The radius is given as,
r = 36 / 2
r = 18 inches
The area of the circle is given as,
A = π x (18)²
A = 3.14 x 324
A = 1,017.36 square inches
The number of square inches of cloth cut from the square will be 1,017.36 square inches. Then the correct option is A.
More about the area of a circle link is given below.
https://brainly.com/question/11952845
#SPJ1
The complete question is given below.
A circle is cut from a square piece of cloth, as shown:
A square, one side labeled as 36 inches, has a circle inside it. The circle touches all the sides of the square. The portion of the square outside the circle is shaded.
How many square inches of cloth is cut from the square?
(π = 3.14)
1,017.36 in2
1,489.24 in2
1,182.96 in2
1,276.00 in2
a quantity with an initial value of 510 grows exponentially at a rate such that the quantity doubles every 8 decades. what is the value of the quantity after 7 years, to the nearest hundredth?
Answers
After five decades, the amount is worth to the nearest hundredth is 607.54
Any decimal number is rounded to the nearest hundredth by the term "to the nearest hundredth." A hundredth is 1/100 or 0.01 in decimal form. For instance, 2.17 is the result of rounding 2.167 to the nearest tenth.
Look at the next place value to the right in order to round a number to the closest hundredth (the thousandths this time). The same applies: Simply eliminate all the digits to the right if the number is 4 or fewer. Add 1 to the digit in the hundredths place if the number is five or above, and then eliminate all the digits to the right.
The equation below can be used to describe this amount at intervals of 2t decades. where r is the rate of increase and Q(0) is the initial quantity. A 510-valued quantity increases exponentially at a rate of 7% every 20 years. After five decades, the amount is worth 607.54
Q(t)=Q(0)\(e^{xt}\)
Q(2.5)= 510e^(0.07*2.5)
= 607.54
Learn more about exponentially Visit : brainly.com/question/2456547
#SPJ4
If line segment AB is the perpendicular bisector of line segment XY at point P,
check all of the correct conclusions that can be made.

Answers
Answer: xp=py
<xpa=<apy
4 right angles are formed
2(xp)=xy
<xpa and <apy are supplements.
Step-by-step explanation:
3. The system of equations for two liquid surge tanks in series is
A₁ dh'₁/dt = q'ᵢ - 1/R₁ h'₁, q'₁ = 1/R₁ h'₁
A₂ dh'₂/dt = 1/R₁ h'₁ - 1/R₂ h'₂ q'₂ = 1/R₂ h'₂
Using state-space notation, determine the matrices A,B,C, and D assuming that the level deviations are the state variables: h'₁ and h'₂. The input variable is q'ᵢ , and the output variable is the flow rate deviation, q'₂.
Answers
The surge tank is a vital component of a system in which the flow rate fluctuates significantly. The flow rate entering the tank varies significantly, causing the fluid level in the tank to fluctuate as a result of the compressibility of the liquid. The surge tank is utilized to reduce pressure variations generated by a rapidly fluctspace uating pump flow rate. To determine the matrices A,B,C, and D using state-space notation, here are the steps:State representation is given by:dx/dt = Ax + Bu; y = Cx + DuWhere: x represents the state variablesA represents the state matrixB represents the input matrixC represents the output matrixD represents the direct transmission matrixThe equation can be written asA = [ -1/R₁ 0; 1/R₁ -1/R₂]B = [1/A₁; 0]C = [0 1/R₂]D = 0Thus, the matrices A,B,C and D assuming that the level deviations are the state variables: h'₁ and h'₂. The input variable is q'ᵢ, and the output variable is the flow rate deviation, q'₂ are given by A = [ -1/R₁ 0; 1/R₁ -1/R₂]B = [1/A₁; 0]C = [0 1/R₂]D = 0.Hence, the required matrices are A = [ -1/R₁ 0; 1/R₁ -1/R₂], B = [1/A₁; 0], C = [0 1/R₂], and D = 0 using state-space notation for the given system of equations for two liquid surge tanks.
surge tank: https://brainly.com/question/14143728
#SPJ11
If a coin is flipped 50 times, in how many ways could there be exactly two tails?
Answers
Answer:
if u eat 50 apples in a month how many of them will be bitter or sweat.
Step-by-step explanation:
Answer:
1
Step-by-step explanation:
it has a 50 50 percent chance of landing on tails each time
Donna bought 5 bags of dog treats for $13.10. What is the cost per bag of dog treats?
A. $18.10
B.$3.28
C.$2.62
D.$0.38
Answers
Unit 9 test: Trigonometry
What is the right answer to this problem?

Answers
Answer:
x = 10.5
Step-by-step explanation:
\(cos 65 =\frac {adjacent}{hypotenuse} \\\\0.4226 = \frac{x}{25}\\\\0.4226 \times 25 = x \\\\x = 10.565\)
Answer:
Step-by-step explanation:
take 65 degree as reference angle
using cos rule
cos 65=adjacent/hypotenuse
0.42=x/25
0.42*25=x
10.5=x
You prepare8 scoops of dog food for 4 dogs, and prepare15 scoops of dog food for 6 dogs. Is there a proportional relationship between the number of scoops and the number of dogs?
Choose the correct answer below.
Answers
Answer:
Is there a proportional relationship between the number of scoops and the number of dogs?
No.
Step-by-step explanation:
A proportional relationship is something like:
y = k*x
Here y can represent the number of scoops of dog food, and x the number of dogs.
First, we know that for 4 dogs he prepares 8 scoops of dog food, then:
8 = k*4
If the relationship is proportional, then we should have a similar equation for the case of 6 dogs, where he prepares 15 scoops of dog food:
15 = k*6
So if we have the same k in both equations, then there is a proportional relationship between the number of scoops and the number of dogs.
In the first equation we have:
8 = k*4
8/4 = k
2 = k
And in the second equation we have:
15 = k*6
15/6 = k
2.5 = k
The values of k are different, so no, there isn't a proportional relationship between the number of scoops and the number of dogs.
in exercises 21 and 22, a, b, p, and d are n????n matrices. mark each statement true or false. justify each answer.
Answers
The statement is false since the equation ap = pb does not have a unique solution.
The statement is true because if the matrix equation ap = b has a solution for every n × 1 matrix b, then a must be invertible.
Exercise 21:
a) The equation ap = pb has a unique solution.
False.
To determine the uniqueness of the solution, we need to consider the dimensions of the matrices involved. Let's assume a, b, p are n × n matrices.
If the equation ap = pb has a unique solution, it implies that p can be uniquely determined given the matrices a and b. However, in general, there is no guarantee of a unique solution.
For example, let's consider n = 2. Suppose a = [[1, 0], [0, 1]], b = [[1, 0], [0, 1]], and p = [[2, 0], [0, 2]]. In this case, ap = pb becomes [[2, 0], [0, 2]] = [[2, 0], [0, 2]], which satisfies the equation. However, we could also choose p = [[3, 0], [0, 3]], and it would still satisfy the equation. Therefore, the equation does not have a unique solution.
Exercise 22:
a) If the matrix equation ap = b has a solution for every n × 1 matrix b, then a must be invertible.
True.
If the matrix equation ap = b has a solution for every n × 1 matrix b, it implies that the equation always has a solution regardless of the choice of b. This condition is equivalent to saying that the matrix a is left invertible.
To show that a is invertible, we need to demonstrate that a has a right inverse, denoted as a^(-1). This means there exists a matrix p such that ap = I, where I is the identity matrix.
Let's assume b = I, the n × n identity matrix. Since the equation ap = b has a solution for every n × 1 matrix b, it implies that there exists a matrix p such that ap = I. Therefore, a has a right inverse.
To know more about Matrix, visit
https://brainly.com/question/27929071
#SPJ11
Suppose that x has a beta distribution with parameters a = 2. 1 and ß = 1. Determine to 4 decimal places the following a. P(X < 0. 21) b. P(0. 21 < X < 0. 76) c. Mean d. Variance
Answers
A) To 4 decimal places, the variance ≈ 0.0383.
B) , P(0.21 < X < 0.76) ≈ 0.8054.
C) The mean ≈ 0.6774.
D) The variance ≈ 0.0383.
a. To find P(X < 0.21), we can use a cumulative distribution function (CDF) calculator for the beta distribution with parameters a = 2.1 and b = 1. Using such a calculator, we get:
P(X < 0.21) ≈ 0.0668
Therefore, to 4 decimal places, the variance ≈ 0.0383.
b. Similarly, to find P(0.21 < X < 0.76), we can use the beta distribution CDF calculator and subtract the probability of X being less than 0.21 from the probability of X being less than 0.76. That is,
P(0.21 < X < 0.76) = P(X < 0.76) - P(X < 0.21)
Using the same beta distribution CDF calculator, we get:
P(0.21 < X < 0.76) ≈ 0.8722 - 0.0668 ≈ 0.8054
Therefore, to 4 decimal places, P(0.21 < X < 0.76) ≈ 0.8054.
c. The mean of a beta distribution with parameters a and b is given by:
Mean = a / (a + b)
Substituting a = 2.1 and b = 1, we get:
Mean = 2.1 / (2.1 + 1) ≈ 0.6774
Therefore, to 4 decimal places, the mean ≈ 0.6774.
d. The variance of a beta distribution with parameters a and b is given by:
Variance = (a * b) / [(a + b)^2 * (a + b + 1)]
Substituting a = 2.1 and b = 1, we get:
Variance = (2.1 * 1) / [(2.1 + 1)^2 * (2.1 + 1 + 1)] ≈ 0.0383
Therefore, to 4 decimal places, the variance ≈ 0.0383.
Learn more about variance here:
https://brainly.com/question/32159408
#SPJ11
28/49 in its simplified form?
Answers
\( \large \mathfrak{Answer : }\)
Simplified form of the above fraction is :
\( \dfrac{28}{49} \)\( \dfrac{4}{7} \)Answer: the simplest form is 4/7
Step-by-step explanation:
Ken is traveling for his business. He has a new 0.85- ounce tube of toothpaste that’s supposed to last him the whole trip. The amount of toothpaste Ken squeezes out of the tube each time he brushes is independent, and can be modeled by a Normal distribution with mean 0.13 ounce and standard deviation 0.02 ounce. If Ken brushes his teeth six times on a randomly selected trip, what’s the probability that he’ll use all the toothpaste in the tube?
Answers
The probability that Ken will use all the toothpaste in the tube is 7.64%.
From the given information,Mean, μ = 0.13 ounceStandard deviation, σ = 0.02 ounceNumber of times Ken brushes his teeth, n = 6.
The amount of toothpaste Ken squeezes out of the tube each time he brushes is independent and can be modeled by a Normal distribution.
From this information, we can obtain that:Mean of toothpaste used in 6 brushes = n × μ = 6 × 0.13 = 0.78 ounceStandard deviation of toothpaste used in 6 brushes = $\sqrt{n}$ × σ = $\sqrt{6}$ × 0.02 = 0.049 ounce.
To find the probability that Ken will use all the toothpaste in the tube, we need to calculate the probability of the amount of toothpaste used in 6 brushes being more than or equal to 0.85 ounce,
which is the total amount of toothpaste in the tube.P(X ≥ 0.85) = P( Z ≥ (0.85 - 0.78) / 0.049) = P(Z ≥ 1.43) = 1 - P(Z < 1.43)Using standard normal distribution table, we find the value of P(Z < 1.43) as 0.9236. Therefore,P(X ≥ 0.85) = 1 - P(Z < 1.43) = 1 - 0.9236 = 0.0764 or 7.64%.
The amount of toothpaste that Ken squeezes out each time he brushes is modeled by a normal distribution with mean 0.13 ounces and standard deviation 0.02 ounces.
The amount of toothpaste squeezed out at each brushing is independent of the previous amount of toothpaste squeezed out. We want to determine the probability that Ken will use all of the toothpaste in a 0.85-ounce tube if he brushes his teeth six times.
To do so, we first find the mean and standard deviation of the amount of toothpaste squeezed out in six brushes. If Ken brushes his teeth six times, then the mean amount of toothpaste squeezed out is nμ = 6(0.13) = 0.78 ounces. If the amount of toothpaste squeezed out at each brushing is independent, then the standard deviation of the amount of toothpaste squeezed out in six brushes is sqrt(6) * 0.02 = 0.049 ounces.
We now want to find the probability that Ken will use all of the toothpaste in the tube.
This is equivalent to finding the probability that the amount of toothpaste squeezed out in six brushes is greater than or equal to 0.85 ounces, which is the total amount of toothpaste in the tube.
If X is the amount of toothpaste squeezed out in six brushes, then we want to find P(X >= 0.85).We can standardize the distribution of X by subtracting the mean and dividing by the standard deviation.
Z = (X - μ) / σ is the standard normal random variable associated with X. In this case, Z has mean 0 and standard deviation 1. We want to find P(Z >= (0.85 - 0.78) / 0.049), which simplifies to P(Z >= 1.43). Using a standard normal distribution table, we can find P(Z < 1.43) = 0.9236. Therefore, P(Z >= 1.43) = 1 - P(Z < 1.43) = 1 - 0.9236 = 0.0764, or 7.64%.Therefore, the probability that Ken will use all the toothpaste in the tube is 7.64%.
Therefore, the probability that Ken will use all the toothpaste in the tube is 7.64%.
To know more about Normal distribution visit:
brainly.com/question/15103234
#SPJ11
In PQR, what is the m

Answers
Answer:
105°
Step-by-step explanation:
(11x-5)+(6x+5)+x=180
18x=180
x=10°
m∠Q=11x-5=11*10-5=105°
Please help!!!! Giving brainliest and extra points!!!! (Click on the photo)

Answers
Answer:
i dont understand the question much cuz its only told berries so i think is both rasberry and strawberry
Step-by-step explanation:
if so here my solve: Both berries are 38% of the graph, we have equation 38%×290 = 110,2
hmmmm maybe the ans is D. 110
Find all missing angles

Answers
Answer: 1=95 2=85 3=95 4=85 5=36 6=49
Step-by-step explanation:
jeff paid $4773 for 6 identical printers and 3 identical cameras. ron bought 4 such printers and 6 such cameras and paid $5002 in all. what is the cost of each printer?
Answers
The cost of each printer is $568.
Find cost per unitTo find the cost of each printer, we need to use a system of equations.
Let's call the cost of each printer "p" and the cost of each camera "c".
The first equation we can create is: 6p + 3c = 4773
The second equation we can create is: 4p + 6c = 5002
Now we can use the elimination method to solve for one of the variables.
Let's eliminate the "c" variable by multiplying the first equation by -2: -12p - 6c = -9546
And then add the two equations together: -8p = -4544
Now we can solve for "p" by dividing both sides by -8: p = 568
So the cost of each printer is $568.
To find the cost of each camera, we can plug the value of "p" back into one of the original equations and solve for "c":
6(568) + 3c = 4773
3408 + 3c = 4773
3c = 1365
c = 455
So the cost of each camera is $455.
Therefore, the cost of each printer is $568 and the cost of each camera is $455.
Learn more about unit cost at https://brainly.com/question/29355214
#SPJ11
Suppose that the probability of event A is 0.4 and the probability of event B is 0.5. What is P A B ( ) ? if A and B are mutually exclusive? What is P A B ( ) ? if A and B are independent?
Answers
If A and B are independent, they cannot be mutually exclusive. In this case, P(A ∩ B) = P(A) * P(B), but since A and B cannot be mutually exclusive, this situation is not applicable.
If A and B are mutually exclusive events, it means that they cannot occur at the same time. Therefore, P(A and B) is equal to zero, because the intersection of the events is empty. So, if A and B are mutually exclusive:
P(A ∩ B) = 0
If A and B are independent events, it means that the occurrence of one event does not affect the probability of the other event occurring. In this case, the probability of both events occurring can be calculated as:
P(A ∩ B) = P(A) * P(B)
However, since A and B are mutually exclusive, they cannot be independent. If two events are mutually exclusive, the occurrence of one event implies that the other event cannot occur. Therefore, if A and B are mutually exclusive, they cannot be independent.
So,
If A and B are mutually exclusive, P(A ∩ B) = 0 and it does not make sense to talk about the probability of both events occurring together.
If A and B are independent, they cannot be mutually exclusive. In this case, P(A ∩ B) = P(A) * P(B), but since A and B cannot be mutually exclusive, this situation is not applicable.
Learn more about probability here, https://brainly.com/question/25839839
#SPJ11
Eva is short on frosting! She works in a bakery and has 12 cakes to frost, but she is short 4 1/8 cups on the amount of frosting required.She decides that she will spread the frosting she has among the 12 cakes. She makes a sign for the cakes and names them by the value that represents the amount of frosting on each cake compared to the amount it should have.What does the sign say?Drag a value to the box to correctly complete the statement.Calvin digs a hole at a steady rate of 1 1/3 feet every hour.Consider ground level to be 0.What value represents the elevation of the hole relative to ground level after digging for 2 1/2 hours?The morning temperature in northern Canada was −28.9∘ F. The temperature rose 33.2°F during the day before reaching its high temperature for the day.What was the high temperature for the day?
Answers
The question are based on fraction manipulation, hence, the answers to the questions are :
Decrease in frosting per cake = \( \frac{11}{32} \: cups \)Depth of hole = \( 3 \frac {1}{3} \: feets \) Final temperature = 4.3°FThe number of cakes to frost = 12
Shortage on amount of frosting required = \( 4\frac{1}{8} = \frac{33}{8}\)
To apportion the shortage on all 12 cakes ;
\( \frac{33}{8} \div 12 = \frac{33}{8} \times \frac{1}{12} = \frac{33}{96} = \frac{11}{32}\)2.)
Digging rate = \( 1\frac{1}{3} \: feets = \frac{4}{3} \: feets \: per \: hour \)
Digging time = \( 2\frac{1}{2} \: hours = \frac{5}{2} \: hours \)
Depth of hole = Digging rate × digging time
Depth of hole =\( \frac{4}{3} \times \frac{5}{2} = \frac{20}{6} = 3 \frac {1}{3} \)
3.)
Current temperature value = - 28.9°F
Change or Rise in Temperature = 33.2°F
Final temperature = High temperature for the day.
Hence,
High temperature = Current temperature + Rise in temperature
High temperature = - 28.9°F + 33.2°F = 4.3°F
Therefore, the high temperature value for the day is 4.3°F
Learn more :https://brainly.com/question/13497040
Answer:
4.3
or in other words
The questions are based on fraction manipulation, hence, the answers to the questions are :
Decrease in frosting per cake =
Depth of hole =
Final temperature = 4.3°F
The number of cakes to frost = 12
Shortage on amount of frosting required =
To apportion the shortage on all 12 cakes ;
2.)
Digging rate =
Digging time =
Depth of hole = Digging rate × digging time
Depth of hole =
3.)
Current temperature value = - 28.9°F
Change or Rise in Temperature = 33.2°F
Final temperature = High temperature for the day.
Hence,
High temperature = Current temperature + Rise in temperature
High temperature = - 28.9°F + 33.2°F = 4.3°F
Therefore, the high temperature value for the day is 4.3°F
Learn more :brainly.com/question/13497040
Step-by-step explanation:
~Bye~
also have a great day!
btw i did the quiz
p.s plz give brainliest!
thank you
NEXT!
lol bye
~~~~~~~TTTTTTT_______