z varies directly as square-root of x and inversely as y. If z = 147 when x = 16 and y = 6, find z if x = 25 and y = 4. (Round off your answer to the nearest hundredth.)
Answers
SOLUTION
From the question
\(\begin{gathered} z\propto\sqrt[]{x}\text{ and } \\ z\propto\frac{1}{y} \\ \text{combining we have } \\ z\propto\frac{\sqrt[]{x}}{y} \\ \propto\text{ is a proportionality constant } \end{gathered}\)Removing the proportionality sign and introducing a constant, we have
\(\begin{gathered} z=k\times\frac{\sqrt[]{x}}{y} \\ z=\frac{k\sqrt[]{x}}{y} \end{gathered}\)Making k the subject, we have
\(\begin{gathered} z=\frac{k\sqrt[]{x}}{y} \\ k\sqrt[]{x}=yz \\ k=\frac{yz}{\sqrt[]{x}} \end{gathered}\)Substituting the initial values of z, x, and y, we have
\(\begin{gathered} k=\frac{yz}{\sqrt[]{x}} \\ k=\frac{6\times147}{\sqrt[]{16}} \\ k=\frac{882}{4} \\ k=220.5 \end{gathered}\)The relationship becomes
\(z=\frac{220.5\sqrt[]{x}}{y}\)Substituting the second values of x and y into the equation for the relationship, we have
\(\begin{gathered} z=\frac{220.5\sqrt[]{x}}{y} \\ z=\frac{220.5\sqrt[]{25}}{4} \\ z=\frac{220.5\times5}{4} \\ z=\frac{1,102.5}{4} \\ z=275.625 \end{gathered}\)Hence the answer is 275.63 to the nearest hundredth
Related Questions
help with the Measure of a triangle’s side

Answers
Answer:
x = 163.5
x = 1.2
Step-by-step explanation:
Recall: SOH CAH TOA
For the first triangle:
Reference angle = 73°
Opposite = x
Adjacent = 50
Apply TOA:
Tan 73° = Opp/Adj
Tan 73° = x/50
50*Tan 73° = x
163.542631 = x
x = 163.5 (nearest tenth)
For the first triangle:
Reference angle = 4°
Opposite = x
Adjacent = 17
Apply TOA:
Tan 4° = Opp/Adj
Tan 4° = x/17
17*Tan 4° = x
1.1887558 = x
x = 1.2 (nearest tenth)
he polynomial of degree 5, P ( x ) has leading coefficient 1, has roots of multiplicity 2 at x = 3 and x = 0 , and a root of multiplicity 1 at x = − 1 Find a possible formula for P ( x ) .
f]
Answers
The possible formula for the polynomial in discuss whose roots are described as; having roots of multiplicity 2 at x = 3 and x = 0 , and a root of multiplicity 1 at x = − 1 is; P(x) = x^5 -5x⁴-6x³+18x².
What is the polynomial in discuss whose roots and leading coefficient are as discussed?The polynomial which is as described in the task content whose roots are as given can be written in its factorised form as follows;
P(x) = (x-3) (x-3) (x) (x) (x+1)
The expanded form is therefore;
P(x) = x^5 - 5x⁴- 6x³+ 18x².
Therefore, the polynomial having roots of multiplicity 2 at x = 3 and x = 0 , and a root of multiplicity 1 at x = − 1 is P(x) = x^5 - 5x⁴- 6x³+ 18x².
Read more on polynomials;
https://brainly.com/question/13793580
#SPJ1
The circumference of a circular glazed donut with rainbow sprinkles is 9.42 inches. What is the diameter and radius of the circular donut?
Answers
The formula for the circumference of a circle is given by 2 * pi * r, where r is the radius. If the circumference is 9.42 inches, then we can write the equation:
9.42 = 2 * pi * r
Solving for r, we get:
r = 9.42 / (2 * pi)
The diameter of the circle is equal to 2 * r, so:
d = 2 * r = 2 * (9.42 / (2 * pi)) = 9.42 / pi
So, the radius of the circular donut is approximately 3 inches, and the diameter is approximately 9.42 inches.
A dressmaker needs to cut 9-inch pieces of ribbon from rolls of ribbon that are 9 feet in length. How many 9-inch pieces can the dressmaker cut from 10 of these rolls of ribbon?
Before you try that problem, answer the question below.
How many \textbf{inches}inches of ribbon does the dressmaker have, in total?
Answers
Answer: 12
Step-by-step explanation:
There are 108 inches in 9 feet and then you divide 108 by 9
a book sold 35,800 copies in its first month of release. suppose this represents 9.7% of the numbers of copies sold to date. how many copies have been sold to date?
round answer to nearest whole number
Answers
The answer is 369,072. This is the total number of copies sold to date.
What is equation?An expression that uses symbols to represent the relationship between two or more values.
This is calculated by solving the equation 9.7% × x = 35,800, where x is the total number of copies sold to date.
To solve this equation, we first need to convert the percentage to a decimal.
To do this, we divide 9.7 by 100, giving us 0.097.
We can then multiply both sides of the equation by this decimal, giving us 0.097x = 35,800.
We can then solve for x by dividing both sides of the equation by 0.097. This gives us x = 369,072. This is the total number of copies sold to date.
For more questions related to expression
https://brainly.com/question/4344214
#SPJ1
g(x)
12 fy
10
88
8
6
4
4-3-2-12
-8
10
-1²1
f(x)
4 5 6 x
Which statement is true regarding the functions on the
graph?
Of(6) = g(3)
f(3) = g(3)
f(3) = g(6)
f(6) = g(6)
PLEASE HURRY IM TIMED!!!!

Answers
Answer: f(3) = g(6)
Step-by-step explanation: if you plug them in we see that f of 3 on the y axis intercept g of x so we then go up and see that g of 6 intercepts f of 3 so therefore that is the answer
Work out the bearing of D from C.

Answers
The bearing of point D from C as required to be determined in the task content is; 315°.
What is the bearing of point D from C?By definition, the bearing of a point is the number of degrees in the angle measured in a clockwise direction from the north line to the line joining the centre of the compass with the point. A bearing is characteristically used to represent the direction of one point relative to another point.
The bearing of the point D from C in this case where the angle motion is clockwise starting from the north pole by convention;
The bearing of D from C is; 360 - 45 = 315°.
Read more on bearing;
https://brainly.com/question/28782815
#SPJ1
Christina is buying a $170,000 home with a 30-year mortgage. She makes a $20,000 down payment.
Use the table to find her monthly PMI payment.
A. $51.25
B. $37.50
C. $23.75
D. $42.50

Answers
The monthly PMI Payment for Christina's loan is $37.50.The correct answer is option B.
To determine Christina's monthly PMI (Private Mortgage Insurance) payment, we need to find the corresponding interest rate for her loan-to-value (LTV) ratio. The LTV ratio is calculated by dividing the loan amount by the property value.
The loan amount can be calculated by subtracting the down payment from the property value:
Loan amount = Property value - Down payment
= $170,000 - $20,000
= $150,000
Now we can calculate the LTV ratio:
LTV ratio = Loan amount / Property value * 100
= $150,000 / $170,000 * 100
= 88.24%
Since Christina is obtaining a 30-year mortgage, we need to look at the interest rates for LTV ratios between 85.01% and 90%. According to the table, the interest rate for this range is 0.30%.
To calculate the PMI payment, we multiply the loan amount by the PMI rate and divide it by 12 months:
PMI payment = (Loan amount * PMI rate) / 12
= ($150,000 * 0.30%) / 12
= $450 / 12
= $37.50
For more such questions on Payment,click on
https://brainly.com/question/25793394
#SPJ8
The Probable question may be:
Christina is buying a $170,000 home with a 30-year mortgage. She makes a $20,000 down payment.
Use the table to find her monthly PMI payment
Base to loan% = 95.01% to 97%,90.01% to 95%,85.01% to 90%,80.01% to 85%.
30-year fixed-rate loan = 0.55%,0.41%,0.30%,0.19%
15-year fixed-rate loan = 0.37%,0.28%,0.19%,0.17%.
A. $51.25
B. $37.50
C. $23.75
D. $42.50
Let f(x)=x2+8x. Evaluate f(x)=--16
Answers
Answer:
-384
Step-by-step explanation:
f(x) =x^2+8x
evaluate f(x)=-16
input -16 for x
-16^2+8(-16)
-16^2= -256
then, 8*-16=-128
add the two negatives
-256+-128= -384
what is the arithmetic sequence for 128,96,64,32 fraction form
Answers
--------------------
4n-1Step-by-step explanation:
128 and r = 3 over 4 (127,) . (3 over 4) apply the product rule to 3 over 4 and I don't kno the rest but that's ita triangular pyramid with an equilateral base has a side length of 10 centimeters and a surface area of 214.5 square centimeters. find its slant height.
PLEASE ANSWER ASAP
Answers
Answer:the slant height of the triangular pyramid is approximately 11.4132 centimeters.
(02.02 MC)
If trapezoid ABCD was reflected over the y-axis, reflected over the x-axis, and rotated 180°, where would point A′′′ lie?
Trapezoid formed by ordered pairs A at negative 4, 1, B at negative 3, 2, C at negative 1, 2, D at 0, 1.
(1, −1)
(−4, 1)
(1, 1)
(−4, −1)
Answers
The location of point A''' after the three transformations would be (-4, 1).
To determine the location of point A''', we need to apply the three transformations (reflection over the y-axis, reflection over the x-axis, and rotation of 180°) to point A.
When a point is reflected over the y-axis, the x-coordinate is negated while the y-coordinate remains the same.
So, the reflection of point A (-4, 1) over the y-axis would be (4, 1).
When a point is reflected over the x-axis, the y-coordinate is negated while the x-coordinate remains the same. So, the reflection of point (4, 1) over the x-axis would be (4, -1).
When a point is rotated 180°, the x-coordinate and y-coordinate are both negated. So, the rotation of point (4, -1) by 180° would be (-4, 1).
To learn more on Transformation click:
https://brainly.com/question/11709244
#SPJ1
PLS HELP WILL MARK BRAINLIEST
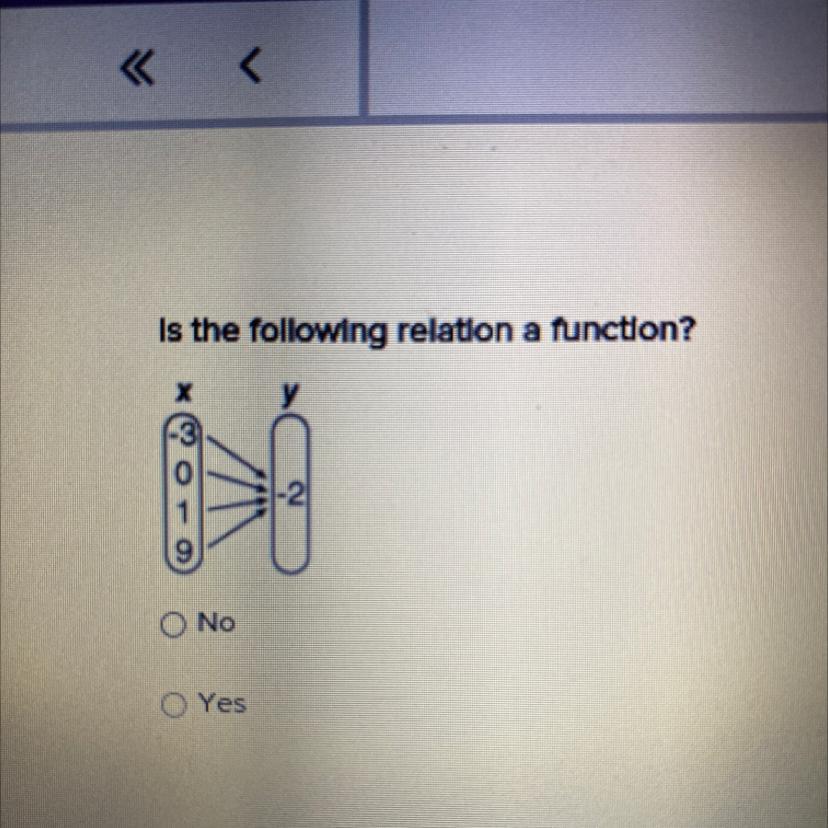
Answers
what is the volume of the box?length:1/2 footwidth: 1/2 foot height:3/4
Answers
This problem is about volume.
Remember that volume can be found by the product of all three dimensions.
In this case, we have
\(l=\frac{1}{2}ft,w=\frac{1}{2}ft,h=\frac{3}{4}ft\)So, the volume is
\(V=l\times w\times h=\frac{1}{2}\times\frac{1}{2}\times\frac{3}{4}=\frac{3}{16}ft^3\)Therefore, the volume of the box is 3/16 cubic feet.Four cups of flour make 5/6 batch of bread. How many cups of flour make 1 batch?
Answers
Answer:
1 and 1/4ths a cup to make a batch if i worded that right
The function f(x)=4^x-6 is transformed to function G through a vertical compression by a factor of 1/2. Complete the equation of function G .  enter the correct answer in the box. Substitute  numerical values into the equation for a and k.
g(x) = a(4)^x-k
Answers
The equation for the transformed function g(x) is: g(x) = 2.323 (4) raise to the power x-0.872/2
How to solve a function?
If the function f(x) is vertically compressed by a factor of 1/2, the equation for the new function g(x) is given by:
g(x) = a(4) raise to the power x-k/2
where "a" and "k" are constants that need to be determined. To find these constants, we can use the fact that the original function f(x) is equal to g(x) when the compression is applied:
f(x) = g(x)/2
Substituting the expression for g(x) into this equation and simplifying, we get:
4raise to the power x - 6 = a(4)raise to the power x-k/2
To solve for "a" and "k", we need to find two equations involving these variables. One way to do this is to evaluate the expression for f(x) at two different values of x, and then set those equal to the corresponding values of g(x)/2. For example, we can choose x = 0 and x = 1:
f(0) = 4 - 6 = -5
f(1) = 4- 6 = -2
Using the equation g(x)/2 = f(x), we can write:
g(0)/2 = -5
g(1)/2 = -2
Substituting the expression for g(x) into these equations, we get:
a(4) raise to the power -k/2 = -10
a(4) raise to the power 1-k/2 = -4
Taking the ratio of these two equations, we can eliminate the variable "a" and solve for "k":
(4)raise to the power -k/2 / (4) raise to the power 1-k/2 = -10 / -4
Simplifying this equation, we get:
4.raise to the power(1-k/2) = 5
Taking the logarithm of both sides (with base 4), we get:
1-k/2 = log4(5)
Solving for "k", we get:
k = 2 - 2 log4(5)
Substituting this value of "k" back into one of the equations we derived earlier, we can solve for "a":
a = -10 / (4) raise to the power -k/2
Substituting the numerical value of "k", we get:
k = 2 - 2 log4(5) ≈ 0.872
a = -10 / (4) raise ti the power -k/2 ≈ 2.323
Therefore, the equation for the transformed function g(x) is:
g(x) = 2.323 (4)raise to the power x-0.872/2
or equivalently:
g(x) = 1.1615 (4) raise to the power -x0.872
To know more about functions visit :-
https://brainly.com/question/11624077
#SPJ1
Answer:
g(x) = 1/2 (4)^x - 3
Step-by-step explanation:
A vertical compression by a factor of 1/2
means that the entire function f is multiplied by 1/2:
1/2 f (x) = 1/2 (4^x - 6)
= 1/2 (4)^x - 3
Simplify the following: (10 + 43 -5) ÷6+5²
A. 30
B. 48/121
C. 33
D. 53/31
Answers
Answer: C 33
Step-by-step explanation:
Cost of windows in Orange is Rs.45. a) find the cost of one score orange. b) how many orange can be purchased for Rs.60.
Answers
16 oranges can be purchased in linear equation.
What in mathematics is a linear equation?
A linear equation is a first-order (linear) term plus a constant in the algebraic form y=mx+b, where m is the slope and b is the y-intercept. Sometimes, the aforementioned is referred to as a "linear equation of two variables," where x and y are the variables.
Equations with variables of power 1 are referred to as linear equations. One example with only one variable is where ax+b = 0, where a and b are real values and x is the variable.
cost of 12 oranges = 45
Thus, number if oranges we will get for ₹1 = 12/45 oranges.
Thus, the number of oranges that we can buy fro ₹60 = (12/45) × 60 = 16.
Thus, 16 oranges can be purchased.
Learn more about linear equation
brainly.com/question/11897796
#SPJ9
tial growth and decay: word problems UKG
You have prizes to res
In Booneville, the use of landlines has been declining at a rate of 20% every year. If there are
25,300 landlines this year, how many will there be in 5 years?
If necessary, round your answer to the nearest whole number.
landlines
Answers
Using an exponential function, it is found that there will be 8290 landlines in 5 years.
What is an exponential function?A decaying exponential function is modeled by:
\(A(t) = A(0)(1 - r)^t\)
In which:
A(0) is the initial value.r is the decay rate, as a decimal.In this problem, we have that the initial value and the decay rate are given as follows:
A(0) = 25300, r = 0.2.
Hence the function is given by:
\(A(t) = 25300(0.8)^t\)
In t = 5 years, the amount of landlines will be given by:
\(A(5) = 25300(0.8)^5 = 8290\)
More can be learned about exponential functions at https://brainly.com/question/25537936
#SPJ1
Last year the depth of the river was 4.2 feet deep.
This year it dropped 5%.
Find the depth of the river this year to cross it.
Answers
Answer:
3.15 ツ
Step-by-step explanation:
What is the meaning of "each partition P of X defines an equivalence relation on X"?

Answers
The statement indicates that when a set X is partitioned, each partition forms an parity relation by grouping together rudiments that are considered original within each subset, thereby creating distinct and non-overlapping subsets within the original setX.
The statement" each partition P of X defines an parity relation on X" means that when a set X is divided into non-overlapping subsets or partitions, each partition creates an parity relation on the original set X.
An parity relation is a relation that satisfies three parcels reflexivity, harmony, and transitivity. In the environment of partitions, when a set X is divided into subsets, each partition forms an parity relation by grouping together rudiments that partake a common characteristic or property.
Within each partition, the rudiments are considered original or affiliated to each other, and they're distinct from rudiments in other partitions. The meaning of" each partition P of X" refers to every possible way of dividing the set X intonon-overlapping subsets.
It implies that different partitions may live grounded on different criteria or conditions for grouping rudiments.
For more such questions on subsets .
https://brainly.com/question/13265691
#SPJ8
Given the figure at the photo, which angle represents angle 2? CHOOSE ALL THAT APPLY!
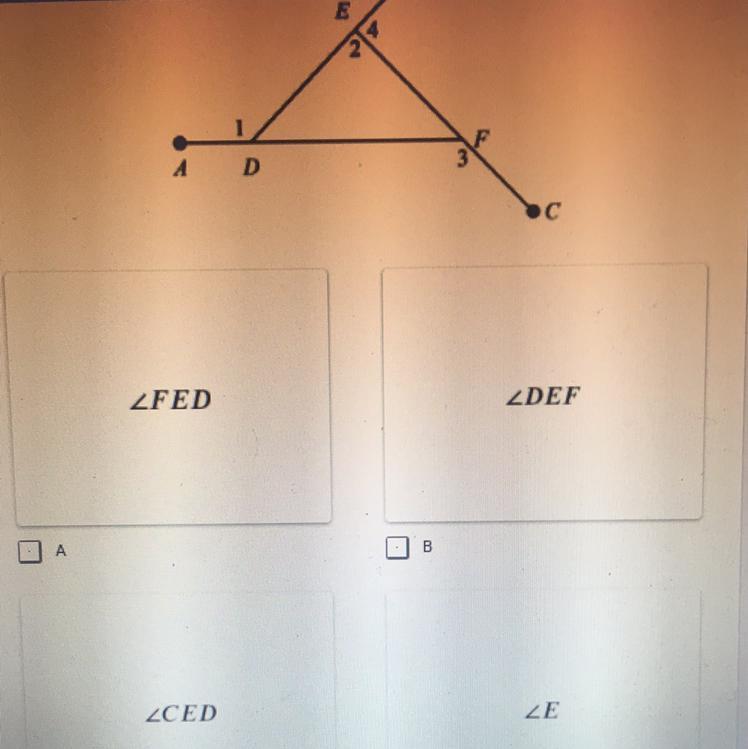
Answers
Answer:
a
Step-by-step explanation:
There is a total of 364 marbles in a jar. The ratio
of blue to red marbles is 3:4. How many red
marbles do you have?
Answers
Answer:
Example 1:
In a bag of red and green sweets, the ratio of red sweets to green sweets is 3:4. If the bag contains 120 green sweets, how many red sweets are there?
Solution:
Step 1: Assign variables :
Let x = red sweets
Write the items in the ratio as a fraction.
red/green
Step 2: Solve the equation
Cross Multiply
3 × 120 = 4 × x
360 = 4x
Isolate variable x
x=360/4
Answer: There are 90 red sweets.
Example 2:
John has 30 marbles, 18 of which are red and 12 of which are blue. Jane has 20 marbles, all of them either red or blue. If the ratio of the red marbles to the blue marbles is the same for both John and Jane, then John has how many more blue marbles than Jane?
Solution:
Step 1: Sentence: Jane has 20 marbles, all of them either red or blue.
Assign variables:
Let x = blue marbles for Jane
20 – x = red marbles for Jane
We get the ratio from John
John has 30 marbles, 18 of which are red and 12 of which are blue.
red/blue
We use the same ratio for Jane.
red/blue
Step 2: Solve the equation
Cross Multiply
3 × x = 2 × (20 – x)
3x = 40 – 2x
Isolate variable x
x=40/5
John has 12 blue marbles. So, he has 12 – 8 = 4 more blue marbles than Jane.
Answer: John has 4 more blue marbles than Jane.
Step-by-step explanation:
Answer:
1
Step-by-step explanation:
Mary has a garden shaped like the figure below. The drawing is not to scale.
22 ft
18 ft
18 ft
11 ft
14 ft
5 ft
What is the area of the garden?
Answers
Answer:
Step-by-step explanation:
Answer:
200
Step-by-step explanation:
14 x 5=70
22 x 4 = 88
14 x 6 =84
84/2= 42
70 + 88 + 42 = 200
Suppose you start with one liter of vinegar and repeatedly remove 0.14 L, replace with water, mix, and repeat. a. Find a formula for the concentration after n steps. b. After how many steps does the mixture contain less than 9% vinegar?
Answers
Formula for the concentration after n steps is \(C(n) = C(0) * (0.86)^n\) and
after 11 steps, the mixture contains less than 9% vinegar.
What is concentration?
Concentration in science refers to the amount of a particular substance (the solute) that is dissolved in a given amount of a solution. It is typically expressed in units of moles per liter (M or mol/L) or as a percentage or fraction of the total solution.
a. Let C(n) be the concentration of vinegar after n steps. At each step, we remove 0.14 L of the mixture, which contains C(n) liters of vinegar. So we are left with (1 - C(n)) liters of water. We then add back 0.14 L of water, giving us a total volume of 1 liter. Therefore, the concentration after one step is:
\(C(1) = C(0) * \frac{1 - 0.14}{1}\)
where C(0) is the initial concentration of vinegar, which is 1 liter per liter or 100%. After two steps, we repeat the process:
C(2) = C(1) * \(\frac{1 - 0.14}{1}\)
Substituting the formula for C(1), we get:
C(2) = C(0) * \((\frac{1 - 0.14}{1}) * (\frac{1 - 0.14}{1})\)
or, more generally:
\(C(n) = C(0) * (0.86)^n\)
b. We want to find the smallest integer n such that C(n) < 0.09 or 9%. Substituting the formula from part (a), we get:
\(C(0) * (0.86)^n < 0.09\)
Dividing both sides by C(0), we get:
\((0.86)^n < 0.09\)
Taking the natural logarithm of both sides, we get:
n * ln(0.86) < ln(0.09)
Dividing both sides by ln(0.86), we get:
n > ln(0.09) / ln(0.86)
Using a calculator, we get:
n > 10.7
Since n must be an integer, the smallest possible value of n is 11. Therefore, after 11 steps, the mixture contains less than 9% vinegar.
To learn more about concentration visit the link:
https://brainly.com/question/17206790
#SPJ1
ba xạ thủ độc lập bắn vào một mục tiêu. xác suất bắn trúng tương ứng là 0,8; 0,7; 0,6. mỗi xạ thủ bắn một viên. gọi X là số viên bắn trúng.
a) lập bảng phân phối xác suất.
b) tính E(X) và VAR(X)
Answers
Answer:
well I don't know
Step-by-step explanation:
your speaking vietnam
Answer:
Step-by-step explanation:

What is the value of x in this figure?
Enter your answer in the box.
x=
Please help meeee!!

Answers
Answer:
x=48°
Step-by-step explanation:
We two lines cross over each other, making four angles, the angles opposite each other are equal. They're called vertically opposite angles.
extra characters:hsjahjshajsjanns
Factor the expression 49t4 - 25 using the polynomial identity (x2 - y2) = (x - y)(x + y)

Answers
Answer:
Step-by-step explanation:
49t^4-25
(7t^2-5)(7t^2+5)
a 2.0-cm-tall object is 15 cm in front of a plano-convex polystyrene plastic lens that has a 13 cm radius of curvature. what are the (a) position and (b) height of the image
Answers
The position of the image is 42.25 cm in front of the lens. and its height is 5.64 cm and inverted.
We can use the thin lens equation to find the position of the image:
\(1/f = 1/d_o + 1/d_i\)
where f is the focal length of the lens, \(d_o\) is the object distance (distance between object and lens), and \(d_i\) is the image distance (distance between image and lens). We can solve for \(d_i\):
\(1/d_i = 1/f - 1/d_o\)
f = R/2 for a plano-convex lens with radius of curvature R, so in this case
\(f = 13 cm/2 = 6.5 cm\).
Plugging in \(d_o\) = 15 cm and f = 6.5 cm, we get:
\(1/d_i = 1/6.5 - 1/15\\1/d_i = 0.1538\\d_i = 6.5/0.1538\\d_i = 42.25 cm\)
So the position of the image is 42.25 cm in front of the lens.
To find the height of the image, we can use the magnification equation:
\(m = -d_i/d_o\)
where m is the magnification (negative for a virtual image), \(d_i\) is the image distance (which we just found), and \(d_o\) is the object distance (given as 15 cm).
\(m = -42.25/15\\m = -2.82\)
This means that the image is 2.82 times smaller than the object. Since the object is 2.0 cm tall, the height of the image is:
\(h_i = mh_o\\h_i = -2.822.0 cm\\h_i = -5.64 cm\)
The negative sign indicates that the image is inverted (upside down). So the position of the image is 42.25 cm in front of the lens, and its height is 5.64 cm and inverted.
For more question on lens equation click on
https://brainly.com/question/25020197
#SPJ4
What is the distance between 1.5 and -2
Answers
Answer:
-1.5,0,1
Step-by-step explanation: