You have used the Distributive Property totransform numerical expressions such as (5)(3) +(2)(3) to (5 + 2)(3). How would you transform 5x +2x into a single term? Substitute five differentvalues into the expressions 5x + 2x and 7x - 1.What do you notice about the values of theexpressions? Is there any value that would fake.the two expressions equal? Why or why not?

The graph of f(x) is the second one, so the correct option is B.

Here we have f(x), a piecewise function, and we want to see which one of the four graphs is the correct one.

You can see that the first domain of the function is:

x ≤ -4

So we must have a closed circle at x = -4, when the parabola ends.

The second domain is:

-4 < x < 1

So x here is not equal to -4 nor 1, so this part starts and ends with open circles.

finally, the linear part starts with a closed circle.

Also, notice that the line has a negative slope, so it goes down, then we can discard the first option.

Then we can see that the correct option is the second graph.

Learn more about piecwise functions:

https://brainly.com/question/3628123

#SPJ1

Answer:

49.09 miles per day

Step-by-step explanation:

There are 5,280 feet in one mile.

There are 60 seconds in one minute.

3 * 60 = 180 feet per minute

There are 60 minutes in one hour.

180 * 60 = 10,800 feet in one hour.

There are 24 hours in one day.

10,800 * 24 = 259,200 feet per day.

Divide to find how many miles she can walk.

259,200 / 5,280 = 49.09 miles

Best of Luck!

Solving the provided question, we can say that the quadratic equation is \((x - 1)(x^{2} + 3x - 4)\) = \(x^{3} + 2x^{2} - 7x + 4\) and the roots of the polynomial are x = 1, -1, 4.

A quadratic polynomial in a single variable is represented by the equation  \(ax^{2}+bx+c=0\). a 0. Since this polynomial is of second order, the Fundamental Theorem of Algebra guarantees that it has at least one solution. There are both simple and complex solutions.

A quadratic equation is just that—quadratic. It has at least one word that has to be squared, as shown by this. One of the often used solutions for quadratic equations is "ax2 + bx + c = 0." where X is an undefined variable and a, b, and c are numerical coefficients or constants.

the quadratic equation is

\((x - 1)(x^{2} + 3x - 4)\) = \(x^{3} + 2x^{2} - 7x + 4\)

On multiplying,

⇒ \(x (x^{2} + 3x - 4) - (x^{2} + 3x - 4)\)

⇒ \(x^{3} + 3x^{2} - 4x - x^{2} - 3x + 4\)

⇒ \(x^{3} + 2x^{2} - 7x + 4\)

∴ We can say that LHS = RHS.

From given equation, the roots of the equation will be  -

\((x - 1)(x^{2} + 3x - 4)\)

⇒ x - 1 = 0

⇒ x = 1

\(x^{2} + 3x - 4 = 0\)

⇒ \(x^{2} - 4x + x - 4\)

⇒ \(x(x - 4) + 1(x - 4)\)

⇒ (x + 1) (x - 4)

⇒ x = -1, x = 4

To know more about quadratic equation visit:

brainly.com/question/30098550

#SPJ1

Answer:

Step-by-step explanation:

Answer:

Below

Step-by-step explanation:

Find unit rate (since it starts at 0,0)

at 45 seconds  it is 900 bottles

             900 bottles / 45 seconds = 20 bottle / sec

20 bottles / sec * 80 sec = 1600 bottles

Answer:

A. the angular speed is 3771.4 rad/min

b. 5921 rpms

Step-by-step explanation: I just got this same question right on a test.

9514 1404 393

Answer:

  5/8 or 5/9

Step-by-step explanation:

The fraction will be exactly ...

  5/(8 1/2) = 10/17   ⇒   (8 1/2)×(10/17) = 5

__

The fraction will be approximately ...

  5/8 or 5/9

The denominator will be a number that makes (8 1/2)/(denominator) ≈ 1. For that denominator, the numerator will be 5, so that we have ...

  (8 1/2) × (5/denominator) ≈ 5

  (8 1/2)/(denominator) ≈ 1 .  . . . . . . . divide by 5

If we want the denominator to be an integer, we could choose either 8 or 9. If we choose 8, the result will be slightly more than 5; if we choose 9, the result will be slightly less.

  (8 1/2) × (5/8) = 5.3125 ≈ 5

  (8 1/2) × (5/9) = 4.722... ≈ 5

Either 5/8 or 5/9 will give a product of about 5.

Answer:

Step-by-step explanation:

Answer:

Step-by-step explanation:

Cuales es los polígonos?

The probability that the mean of a sample of 40 families will be between 17.1 and 18.1 pounds is given as follows:

0.5874 = 58.74%.

The z-score of a measure X of a variable that has mean symbolized by \(\mu\) and standard deviation symbolized by \(\sigma\) is obtained by the rule presented as follows:

\(Z = \frac{X - \mu}{\sigma}\)

The parameters for this problem are given as follows:

\(\mu = 17.2, \sigma = 2.5, n = 40, s = \frac{2.5}{\sqrt{40}} = 0.3953\)

The probability that the mean of a sample of 40 families will be between 17.1 and 18.1 pounds is the p-value of Z when X = 18.1 subtracted by the p-value of Z when X = 17.1, hence:

\(Z = \frac{X - \mu}{\sigma}\)

By the Central Limit Theorem:

\(Z = \frac{X - \mu}{s}\)

Z = (18.1 - 17.2)/0.3953

Z = 2.28

Z = 2.28 has a p-value of 0.9887.

Z = (17.1 - 17.2)/0.3953

Z = -0.25

Z = -0.25 has a p-value of 0.4013.

Hence:

0.9887 - 0.4013 = 0.5874 = 58.74%.

More can be learned about the normal distribution at https://brainly.com/question/25800303

#SPJ1

Answer:

R = { ( 3 , 1 ) , (4 , 1) , (4 , 2) }

Step-by-step explanation:

Which ordered pairs are in the relation {(x, y) | x > y + 1} on the set {1, 2, 3, 4}

Assuming that:

R should be the set of real numbers such that:

R = { (x,y) | x > y + 1}  on the set {1, 2, 3, 4}

Then:

The ordered pairs for the relation can be computed as:

R = { ( 3 , 1 ) , (4 , 1) , (4 , 2) }

Answer:

C.

Step-by-step explanation:

Answer:

Step-by-step explanation:

When two or more positive numbers are added together, the result or sum is always positive. The sum of a positive and a negative integer can be either positive, negative, or zero.

Answer:

Step-by-step explanation:

Jdhbdzbzvdksksskdjdjhdjdjdjjdjdjjfnfndjffjdjxbbx jasjsjs hahahas

The augmented matrix corresponding to the system of equations in this problem is given as follows:

[-6 -5 -4 7].

[7 -9 -1 -7].

[-9 -3 -6 7].

The first row is constructed according to the coefficients of the first equation, hence it is given as follows:

[-6 -5 -4 7].

The second row is constructed according to the coefficients of the second equation, hence it is given as follows:

[7 -9 -1 -7].

The third row is constructed according to the coefficients of the third equation, hence it is given as follows:

[-9 -3 -6 7].

Hence the matrix is given as follows:

[-6 -5 -4 7].

[7 -9 -1 -7].

[-9 -3 -6 7].

More can be learned about a system of equations at https://brainly.com/question/13729904

#SPJ1

Answer:

\(w^{22}\)

Step-by-step explanation:

\((w^3)^4\cdot(w^5)^2=w^{3*4}\cdot w^{5*2}=w^{12}\cdot w^{10}=w^{12+10}=w^{22}\)

The hypotheses to test if this sample indicates a significant change in the average number of hours spent studying is:

0: µ = 14 (null hypothesis)

1: µ ≠ 14 (alternative hypothesis)

Option B is the correct answer.

We have,

The null hypothesis states that the population mean for the number of hours spent studying by full-time students at 4-year colleges in the United States is equal to 14 hours per week,

while the alternative hypothesis states that it is different from 14 hours per week.

By using a two-tailed test, we are checking for any significant change in either direction, whether the average number of hours spent studying has increased or decreased from 14 hours per week.

Thus,

The hypotheses to test if this sample indicates a significant change in the average number of hours spent studying is:

0: µ = 14 (null hypothesis)

1: µ ≠ 14 (alternative hypothesis)

Learn more about hypothesis testing here:

https://brainly.com/question/30588452

#SPJ1

The answer would be (C) 20.

Answer:

The 2nd quartile, also known as the median, is the middle value of a dataset, or the value that separates the lower half of the data from the upper half. In a box-and-whisker plot, the 2nd quartile is represented by the line in the middle of the box.

In the given box-and-whisker plot, the 2nd quartile is 12.5, which is the middle value of the data set. This can be determined by looking at the scale on the x-axis and finding the value that is in the middle of the box.

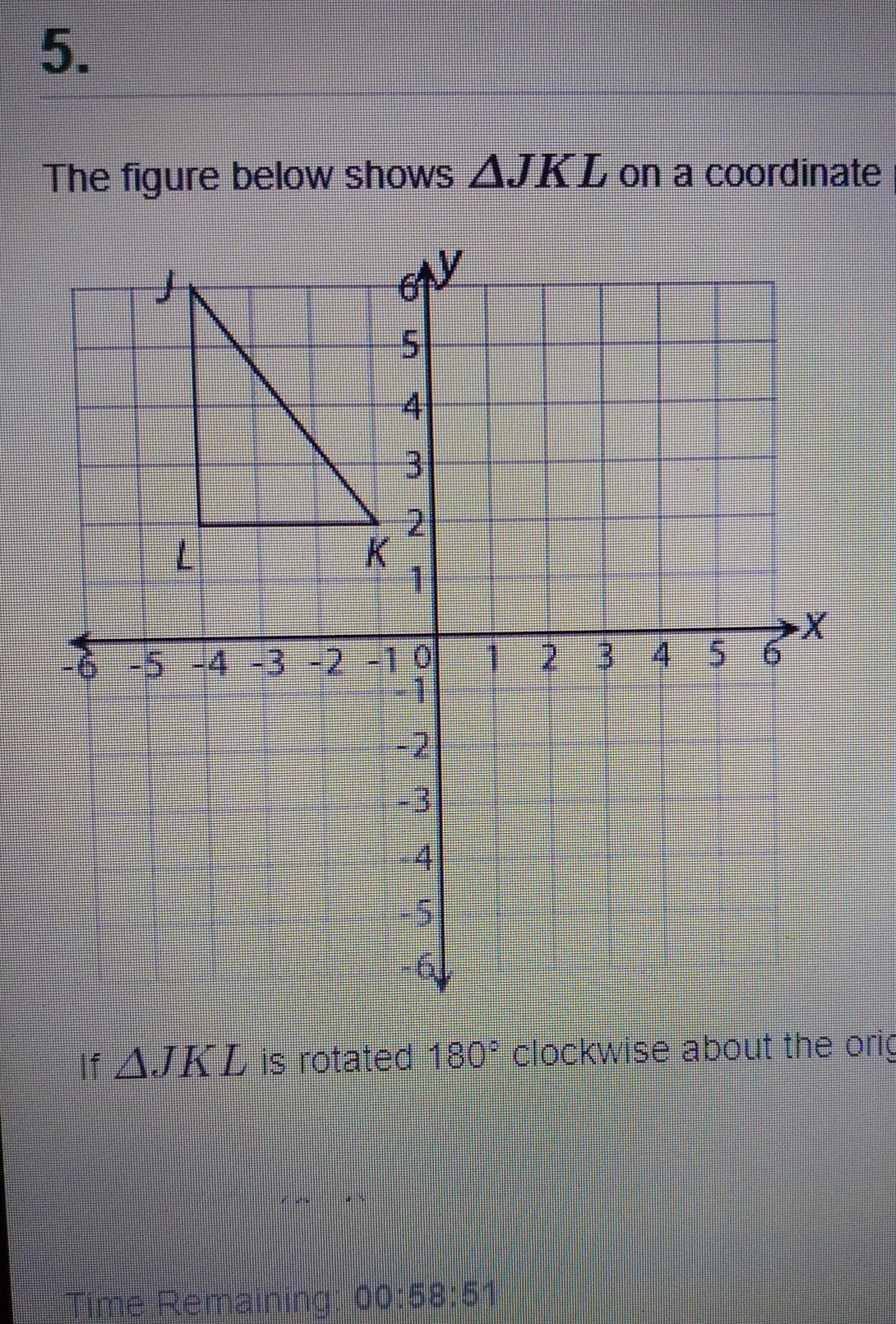
Option B, 12.5, is the correct answer.

Step-by-step explanation:

Answer: any values between a and 3a

Step-by-step explanation:

To determine the possible side lengths for the third side of the triangle, we need to use the Triangle Inequality Theorem. This theorem states that for any triangle, the sum of the lengths of any two sides must be greater than the length of the third side.

Let's call the length of the third side x. Then, based on the Triangle Inequality Theorem, the following two inequalities must be true:

a + 2a > x (the sum of the first and second sides is greater than the third side)

a + x > 2a (the sum of the first and third sides is greater than the second side)

2a + x > a (the sum of the second and third sides is greater than the first side)

Solving the first inequality for x gives us:

x < 3a

Solving the second inequality for x gives us:

x > a

Solving the third inequality for x gives us:

x > -a

Combining these three results, we find that the possible values for the third side length x are:

a < x < 3a

So, the possible lengths for the third side in terms of a are any values between a and 3a, inclusive.

Answer: 13

Step-by-step explanation:

Answer:

Basic facts:

1foot =12 inch

Step-by-step explanation:

Vidal's treehouse was 6 feet which are 72 inches

Mateo's treehouse was 48 inches

72-48=24

24/12=2      

2 feet and 0 inches

Answer: B

Step-by-step explanation: i got it because i

Answer:

B. (4, -6)

Explanation:

If we rotate a triangle 180° clockwise, we can use the following rule to find the new coordinates of the vertex:

(x, y) ----> (-x, -y)

So, if the initial coordinates of point J are (-4, 6), the new coordinates will be:

( -4, 6) ----> (-(-4), -6) = (4, -6)

Therefore, the answer is B. (4, -6)

Answer: 10

Step-by-step explanation: there are 18 before and then when we add 10 there will be 28 out of 50.

Answer:

0.882

Step-by-step explanation:

Finds out how much grams equal lbs then do 400 times the number you just found then you get your answer

Plz mark brainliest

Answer: B C D

Step-by-step explanation:

Answer:

40 students

Step-by-step explanation:

and all the frequencies

there should one student per tally mark because the tally is measuring grades

Hope that helped!!! k

Answer:

\(\Huge \boxed{40}\)

Step-by-step explanation:

Adding all the frequencies in the frequency distribution gives the total number of students.

\(6+10+8+9+7=40\)

The number of students in class VIII whose marks obtained in an examination are 40.

No the larger the number the steeper the slope. 1 would be a steeper slope than a number less than 1.

Use the definition of absolute value.

\(|x| = \begin{cases} x & \text{if } x \ge0 \\ -x & \text{if } x < 0 \end{cases}\)

The absolute value is always non-negative. So if \(x\) is already non-negative, \(|x|=x\) is unchanged. But if \(x\) is negative, then \(|x|=-x\) because multiplying \(x\) by -1 makes it positive.

Now, if \(x>1\), then by the definition of absolute value,

\(x > 1 \implies x - 1 > 0 \implies \boxed{|x - 1| = x - 1}\)