You are shipping some books to a friend. A small box will hold 6 books. A
large box will hold 18 books. You shipped a total of 54 books in 5 boxes.
How many small boxes and how many large boxes did you use? Define the
variables that you use to write the system.
Answers
Related Questions
Q 42 - The proportion of salary of An and B is 5:3 and that of their use is 9:5. On the off chance that they spare Rs. 2600 and Rs. 1800, then their livelihoods are: A-9000, 5400 B-10000, 6000 C-6000, 3600
Answers
Answer: Let's solve this problem step by step.
First, let's assume the salaries of An and B to be 5x and 3x, respectively, where x is a common multiplier.
According to the given information, they save Rs. 2600 and Rs. 1800, respectively. Since savings come from the remaining portion of their incomes after spending, we can calculate their expenditures as follows:
For An:
Income of An = Salary of An + Savings of An
Income of An = 5x + 2600
For B:
Income of B = Salary of B + Savings of B
Income of B = 3x + 1800
Now, let's consider the proportion of their expenditures. It is given that the proportion of their expenditures is 9:5. So, we can write the following equation:
(Expenditure of An)/(Expenditure of B) = 9/5
Since expenditure is the complement of savings, we have:
[(Income of An - Savings of An)] / [(Income of B - Savings of B)] = 9/5
Substituting the previously derived expressions for income, we get:
[(5x + 2600 - 2600)] / [(3x + 1800 - 1800)] = 9/5
Simplifying the equation, we have:
5x / 3x = 9/5
Cross-multiplying, we get:
5 * 3x = 9 * 3x
15x = 27x
Subtracting 27x from both sides, we have:
0 = 12x
This implies that x = 0, which is not a valid solution. Therefore, there seems to be an error or inconsistency in the given information or equations. Please recheck the problem statement or provide additional information to help resolve the issue.
Write an equation for the following math sentence.
One fourth times the difference of ten and a variable is 2/3.
Answers
Answer:
Step-by-step explanation:
Let x be the variable.
One fourth times the difference of ten and x is 2/3
1/4 (10 - x) = 2/3
10 - x = 3/2
-x = 3/2 - 10
x = -3/2 + 10
x = 13/2
The answer is:
\(\rm{\dfrac{1}{4}(10-d)=\dfrac{2}{3}}\)
Work/explanation:
First, the variable is d
Then, the difference of 10 and d is 10 - d.
One-fourth is 1/4.
The equation is : \(\rm{\dfrac{1}{4}(10-d)=\dfrac{2}{3}}\).
Therefore, this is the required equation.A 6 ounce serving of salmon has the following: 200 kcals, 31 grams of protein, 7 grams of fat and 2 grams of saturated fat. What percentage of saturated fat is found in this serving of salmon
Answers
A 6-ounce serving of salmon has 2 grams of saturated fat. To determine the percentage of saturated fat in the serving of salmon, we divide the amount of saturated fat by the total amount of fat and multiply by 100.
The total amount of fat in the serving is 7 grams. So:2g / 7g × 100% = 28.57%Therefore, 28.57% of the 6-ounce serving of salmon is saturated fat. This information can be helpful for individuals who are monitoring their saturated fat intake due to health concerns such as high cholesterol or heart disease.
Saturated fat is a type of fat that is solid at room temperature and is typically found in animal products such as meat and dairy. Consuming too much saturated fat can contribute to high cholesterol levels and increase the risk of heart disease. It is important to consume a balanced diet and limit intake of saturated and trans fats.
Know more about Saturated fat here:
https://brainly.com/question/1986175
#SPJ11
6. How many planes exist on the surface of this pyramid?
Answers
ABCD is a parallelogram in which / ADC = 105° and side AB is produced to point E as shown in the figure. Find the value of (x + y).
Answers
The value of (x + y) in parallelogram ABCD is equal to 150°.
How to determine the value of (x + y)?Since ABCD is a parallelogram and ∠ADC is equal to 105°. Additionally, side AB in parallelogram ABCD is produced to point E. This ultimately implies that, angle C (∠C) and angle D (∠D) are adjacent angles of parallelogram ABCD:
∠C + ∠D = 180° (supplementary angles).
x + 105° = 180°
x = 180 - 105
x = 75°
Based on alternate interior angles theorem, ∠y is congruent to ∠x. Therefore, we have the following:
∠y ≅ ∠x
y = 75°
(x + y) = (75 + 75)
(x+ y) = 150°.
Read more on parallelogram here: https://brainly.com/question/4459854
#SPJ1
Which ordered pair is not a solution to 2x + 3y = 12?
(0,4)
(3, 2)
(2, 3)
(6,0)
Answers
Answer:
(2,3)
Step-by-step explanation:
(2)(2) + (3)(3) = 13
The correct options are (a) and (d).
What is a system of linear equations?A system of linear equations can be defined as a number of equations needed to solve the equations. For n number of variables n number of equations are required.
The given equation is as below,
2x + 3y = 12 (1)
In order to find the correct answer all the options are considered one by one as follows,
(a) (0, 4)
Substitute x = 0 and y = 4 in equation to get,
LHS = 2× 0 + 3 × 4
= 12
Since LHS = RHS, the given option is correct.
(b) (3, 2)
Substitute x = 3 and y = 2 in equation to get,
LHS = 2× 2 + 3 × 2
= 10
Since LHS ≠ RHS, the given option is not correct.
(c) (2, 3)
Substitute x = 2 and y = 3 in equation to get,
LHS = 2× 3 + 3 × 3
= 13
Since LHS ≠ RHS, the given option is not correct.
(d) (6, 0)
Substitute x = 0 and y = 4 in equation to get,
LHS = 2× 6 + 3 × 0
= 12
Since LHS = RHS, the given option is correct.
Hence, the points satisfying the given equation are (0, 4) and (6, 0).
To know more about linear equation click on,
https://brainly.com/question/11897796
#SPJ2
4. Line Segment AB has endpoints A(3,-2) and B(-3,7). What are the Coordinates of the midpoint of AB
Answers
Answer:
\(\left(0,\:\frac{5}{2}\right)\)
Step-by-step explanation:
Image from Chilimath
hope this helps :-)


solve for x Express your answer as an integers or in simplest radical form 1-x^3=9
Answers
Answer:
\(\large\boxed{\tt x = 2}\)
Step-by-step explanation:
\(\textsf{We are asked to solve for x in the given equation.}\)
\(\textsf{We should know that x is cubed, meaning that it's multiplied by itself 3 times.}\)
\(\textsf{We should isolate x on the left side of the equation, then find x by cubic rooting}\)
\(\textsf{both sides of the equation.}\)
\(\large\underline{\textsf{How is this possible?}}\)
\(\textsf{To isolate variables, we use Properties of Equality to prove that expressions}\)
\(\textsf{are still equal once a constant has changed both sides of the equation. A Cubic}\)
\(\textsf{Root is exactly like a square root, but it's square rooting the term twice instead}\)
\(\textsf{of once.}\)
\(\large\underline{\textsf{For our problem;}}\)
\(\textsf{We should use the Subtraction Property of Equality to isolate x, then cubic root}\)
\(\textsf{both sides of the equation.}\)
\(\large\underline{\textsf{Solving;}}\)
\(\textsf{Subtract 1 from both sides of the equation keeping in mind the Subtraction}\)
\(\textsf{Property of Equality;}/tex]
\(\tt \not{1} - \not{1} - x^{3} = 9 - 1\)
\(\tt - x^{3} = 8\)
\(\textsf{Because x}^{3} \ \textsf{is negative, we should exponentiate both sides of the equation by}\)
\(\textsf{the reciprocal of 3, which is} \ \tt \frac{1}{3} .\)
\(\tt (- x^{3})^{\frac{1}{3}} = 8^{\frac{1}{3}}\)
\(\underline{\textsf{Evaluate;}}\)
\(\tt (- x^{3})^{\frac{1}{3}} \rightarrow -x^{3 \times \frac{1}{3} } \rightarrow \boxed{\tt -x}\)
\(\textsf{*Note;}\)
\(\boxed{\tt A^{\frac{1}{C}} = \sqrt[\tt C]{\tt A}}\)
\(\tt 8^{\frac{1}{3}} \rightarrow \sqrt[3]{8} \rightarrow 2^{1} \rightarrow \boxed{\tt 2}\)
\(\underline{\textsf{We should have;}}\)
\(\tt -x=2\)
\(\textsf{Use the Division Property of Equality to divide each side of the equation by -1;}\)
\(\large\boxed{\tt x = 2}\)
find the indicated z score. the graph depicts the standard normal distribution with mean 0 and standard deviation 1. .9850
Answers
Therefore, the indicated z-score is 2.45.
To find the indicated z-score, we need to use a standard normal distribution table. From the graph, we can see that the area to the right of the z-score is 0.9850.
Looking at the standard normal distribution table, we find the closest value to 0.9850 in the body of the table is 2.45. This means that the z-score that corresponds to an area of 0.9850 is 2.45.
It's important to note that the standard deviation of the standard normal distribution is always 1. This is because the standard normal distribution is a normalized version of any normal distribution, where we divide the difference between the observed value and the mean by the standard deviation.
To know more about standard deviation visit:
https://brainly.com/question/31516010
#SPJ11
the population of a town increased from 3300 in 2008 to 4750 in 2012. find the absolute and relative (percent) increase.
Answers
The population of the town increased by 1450 from 2008 to 2012. The relative increase, expressed as a percentage, is approximately 43.94%.
To find the absolute increase, we subtract the initial population from the final population: 4750 - 3300 = 1450.
Therefore, the population of the town increased by 1450 individuals over the four-year period.
To calculate the relative increase as a percentage, we use the following formula:
Relative Increase (%) = (Absolute Increase / Initial Population) × 100
Substituting the values into the formula, we have:
Relative Increase (%) = (1450 / 3300) × 100 ≈ 43.94%
This means that the population of the town increased by approximately 43.94% from 2008 to 2012.
The relative increase gives us a measure of the percentage change in the population size.
In this case, the town experienced a significant population growth of 43.94% over the four-year period.
This information can be useful for understanding demographic trends, planning infrastructure, and making policy decisions to accommodate the increased population.
Learn more about absolute increase here:
https://brainly.com/question/31780820
#SPJ11
(10pts) find all the solutions to the equations.

Answers
What is an ecosystem?
1. A self-contained living thing
2. A group of interacting 3.individuals from the same species located in the same area
4. All of the biotic and abiotic things within a given area and all of their inteactions
5. A food web
Answers
Answer:
4
Step-by-step explanation:
a store is having a 20% off so on all
merchandise if made buys one item and saves $13 what was the original price of the purchase explain or show your reasonings
Answers
Answer:
If a store is having a 20% off sale
By buying an item you save 20% of the price
If Mai saves $13 on an item she is also saving 20%
$13 = 20% of the price
$65 = 100% of the original price
$65 is your answer!
Trying to get the right number possible. What annual payment is required to pay off a five-year, $25,000 loan if the interest rate being charged is 3.50 percent EAR? (Do not round intermediate calculations. Round the final answer to 2 decimal places.Enter the answer in dollars. Omit $sign in your response.) What is the annualrequirement?
Answers
To calculate the annual payment required to pay off a five-year, $25,000 loan at an interest rate of 3.50 percent EAR, we can use the formula for calculating the equal annual payment for an amortizing loan.
The formula is: A = (P * r) / (1 - (1 + r)^(-n))
Where: A is the annual payment,
P is the loan principal ($25,000 in this case),
r is the annual interest rate in decimal form (0.035),
n is the number of years (5 in this case).
Substituting the given values into the formula, we have:
A = (25,000 * 0.035) / (1 - (1 + 0.035)^(-5))
Simplifying the equation, we can calculate the annual payment:
A = 6,208.61
Therefore, the annual payment required to pay off the five-year, $25,000 loan at an interest rate of 3.50 percent EAR is $6,208.61.
Learn more about loan here: brainly.com/question/32625768
#SPJ11
PLEASE HELP 25 POINTS PLUS BRAINLIEST

Answers
The missing length of the triangle using Pythagoras theorem is; x = 3
How to use Pythagoras Theorem?Pythagoras Theorem is defined as the way in which you can find the missing length of a right angled triangle. The right angle triangle has three sides, the hypotenuse (which is always the longest), Opposite (which doesn't touch the hypotenuse) and the adjacent (which is between the opposite and the hypotenuse).
The formula to find the sides is;
hypotenuse² = opposite + adjacent²
We are given;
Hypotenuse = 5
Opposite = x
adjacent = 4
Thus;
5² = x² + 4²
x² = 5² - 4²
x² = 25 - 16
x = √9
x = 3
We conclude that it is the missing length of the triangle
Read more about Pythagoras Theorem at; https://brainly.com/question/231802
#SPJ1
10% of a water tank fills every 5 minutes. If you are filling a 40 gallon tank, how many gallons will there be in 30 minutes?
Answers
After 30 minutes, there are 24 gallons within the water tank due to cross multiplication.
How to Use Cross Multiplication to Estimate the Filling Time of a Water Tank?
The water tank is filling at a constant rate of 10% tank capacity every 5 minutes, according to the statement. The tank holds 40 gallons of water.The gained capacity is calculated by multiplying the following cross multiplication by the water capacity, which is directly proportional to the filling time:
x ∝ tx = (n / 100) · V × (T / t) (1)Where:
n - The initial capacity percentage of the water tank, expressed as a percentage.V - Total water tank capacity in gallons.T - Time remaining in minutes.t - The starting time in minutes.By substituting the values:
x = [0.1 (40 gal)] x (30 minutes / 5 minutes)x = 24 gallonsTherefore, after 30 minutes, there are 24 gallons within the water tank due to cross multiplication.
To learn more about cross multiplication refer to:
brainly.com/question/15209325
#SPJ1
past records indicate that the probability of online retail orders that turn out to be fraudulent is 0.04. suppose that, on a given day, 20 online retail orders are placed. assume that the number of online retail orders that turn out to be fraudulent is distributed as a binomial random variable. (type an integer or a decimal. round to 4 decimal places.)
Answers
The mean number of online retail orders that turn out to be fraudulent is 0.8 and the standard deviation is 0.876
Given that the number of online retail orders that turn out to be fraudulent is distributed as a binomial random variable with probability of success p = 0.04 and number of trials n = 20.
The mean of a binomial distribution is given by the formula
μ = n × p
Substituting the given values, we get
μ = 20 × 0.04
μ = 0.8
Therefore, the mean number of online retail orders that turn out to be fraudulent is 0.8.
The standard deviation of a binomial distribution is given by the formula
σ = sqrt(n × p × (1 - p))
Substituting the given values, we get
σ = sqrt(20 × 0.04 × 0.96)
σ = sqrt(0.768)
σ = 0.876
Learn more about standard deviation here
brainly.com/question/29156955
#SPJ4
The given question is incomplete, the complete question is:
Past records indicate that the probability of online retail orders that turn out to be fraudulent is 0.04. suppose that, on a given day, 20 online retail orders are placed. assume that the number of online retail orders that turn out to be fraudulent is distributed as a binomial random variable. What are the mean and standard deviation of the number of online retail orders that turn out to be fraudulent?
Write the correct answers.
1) I am an integer in Quadrant
My a-coordinate is less than-1.
My coordinate is more than 2.
My r-coordinate is greater than-3.
• The sum of the absolute values of my coordinates is 5.
Who am 17
) Plot me on the coordinate graph.
Answers
The point (-3, 4) satisfies all the given conditions, and hence, it is the point we are looking for. The integer in Quadrant II.
How do you find a point's coordinates on the Cartesian plane?An ordered pair of integers (x, y), where x is the horizontal coordinate or the abscissa and y is the vertical coordinate or the ordinate, is used to represent a point in the Cartesian plane. With regard to the x-axis and y-axis, a point on the plane may be located using these coordinates.
Let's assume that the point has coordinates (-x, y), where x > 1 and y > 2.
Then, using the distance formula, we have:
r = √(x² + y²)
Since r > -3, we have:
√(x² + y²) > -3
x² + y² > 9
Now, absolute values of the coordinates is 5, we have:
|x| + |y| = 5
Since x < -1, we have -x > 1, which means that:
|x| = -x -1
Substituting this into the equation above, we get:
(-x - 1) + |y| = 5
|x| + |y| = 5
Subtracting -x - 1 from both sides, we get:
|y| = x + 6
Substituting this into the equation x² + y² > 9, we get:
x² + (x + 6)² > 9
2x² + 12x + 27 > 0
This inequality holds for all x.
Therefore, the point (-3, 4) satisfies all the given conditions, and hence, it is the point we are looking for. The integer in Quadrant II.
Learn more about cartesian plane here:
https://brainly.com/question/27927590
#SPJ1

Answer:17
Step-by-step explanation:
If mQH = 108° and m/V = 35°, find mUY

Answers
The measure of angle m<UY is 37 degrees
How to determine the valueTo determine the value of the angle, we have;
The sum of angles on a straight line is 180 degreesAngles at a point is equal to 180 degreesSupplementary angles are angles that sum up to 180 degreesComplementary angles are angles that sum up to 90 degreesFrom the information given, we have that;
m<V + m<U+ m<Q = 180; angles on a straight line
Substitute the values, we have;
108 + m<UY + 35 = 180
collect the like terms, we have;
m<UY = 180 - 143
subtract the values, we get;
m<UY = 37 degrees
Learn more about angles at: https://brainly.com/question/25716982
#SPJ1
Line segment su is dilated to create s'u' using point q as the center of dilation. the scale factor of the dilation is
Answers
The scale factor of the dilation is 2 which can be shown in the details given below.
In geometry, a line segment is bounded with the aid of using awesome factors on a line. Or we are able to say a line phase is a part of the road that connects factors. A line has no endpoints and extends infinitely in each the course however a line phase has constant or particular endpoints.
QS : QS'
= 4 : 8
= QU : QU'
= 5 : 10
= 1 : 2
Then the scale factor is of the dilation is 2 (magnification).
To learn more about line segment check the link below:
https://brainly.com/question/2437195
#SPJ4
Complete question
Line segment SU is dilated to create S'U' using point Q as the center of dilation.
The scale factor of the dilation is:

A bus drives 280 miles in 7 hours, what is the unit rate? (In miles per hour)
Answers
Answer:
40 miles per hour
Step-by-step explanation:
Divide 280(miles) by 7(the hours) to get 40 (miles per hour)
Use Green's Theorem to calculate the circulation of F= yi+2xyj around the unit circle, oriented counterclockwise.
circulation =
Answers
The circulation of the vector field F = yi + 2xyj around the unit circle, oriented counterclockwise, is 0.
To calculate the circulation of the vector field F = yi + 2xyj around the unit circle, oriented counterclockwise, we can use Green's Theorem. Green's Theorem relates the circulation of a vector field around a closed curve to the double integral of the curl of the vector field over the region enclosed by the curve.
The circulation (C) is given by:
C = ∮ F · dr
where F is the vector field and dr is the differential displacement along the curve.
In this case, we have F = yi + 2xyj and the curve is the unit circle.
To apply Green's Theorem, we need to compute the curl of F:
curl(F) = ∂Q/∂x - ∂P/∂y
where P and Q are the components of F.
In this case, P = 0 and Q = 2xy.
Taking the partial derivatives, we have:
∂Q/∂x = 2y
∂P/∂y = 0
Therefore, the curl of F is curl(F) = 2y.
Now, let's evaluate the double integral of the curl of F over the region enclosed by the unit circle:
∬ curl(F) dA
Since the unit circle can be represented using polar coordinates, we have dA = r dr dθ.
The limits of integration for r are from 0 to 1, and for θ from 0 to 2π.
∬ curl(F) dA = ∫[0, 2π] ∫[0, 1] (2r sin(θ)) r dr dθ
Simplifying, we get:
∬ curl(F) dA = 2 ∫[0, 2π] ∫[0, 1] r^2 sin(θ) dr dθ
Evaluating the inner integral with respect to r, we get:
∬ curl(F) dA = 2 ∫[0, 2π] [(1/3) r^3 sin(θ)] evaluated from 0 to 1 dθ
∬ curl(F) dA = 2 ∫[0, 2π] (1/3) sin(θ) dθ
Integrating with respect to θ, we have:
∬ curl(F) dA = 2 [(1/3) (-cos(θ))] evaluated from 0 to 2π
∬ curl(F) dA = 2 [(1/3) (-cos(2π) + cos(0))]
∬ curl(F) dA = 2 [(1/3) (1 - 1)]
∬ curl(F) dA = 0
Therefore, the circulation of the vector field F = yi + 2xyj around the unit circle, oriented counterclockwise, is 0.
Learn more about circle here:
https://brainly.com/question/12930236
#SPJ11
Does (7, 8) make the equation y = x + 5 true?
Answers
Answer:
..
Step-by-step explanation:
no the correct point would be (7,12)
7x1=7
7+5=12
Answer:
nop0e
Step-by-step explanation:
The face of a canadian $20 bill has an area that can be represented by the expression 10x^2+9x-40. determine algebraic expressions that represent the dimensions of the bill.
Answers
The algebraic expressions that represent the dimensions of the Canadian $20 bill can be obtained by factoring the given expression, 10x^2 + 9x - 40.
The factored form of the expression, 10x^2 + 9x - 40, gives us two binomial expressions that represent the dimensions of the bill. The dimensions can be represented as (2x - 5) and (5x + 8).
To determine the dimensions of the bill, we need to factor the given expression, 10x^2 + 9x - 40. The factored form provides us with two binomial expressions that represent the length and width of the bill.
In this case, the factored form of 10x^2 + 9x - 40 is (2x - 5)(5x + 8). This means that the dimensions of the bill can be represented by (2x - 5) and (5x + 8), where 2x - 5 represents the length and 5x + 8 represents the width.
It's important to note that the specific values of x will determine the actual dimensions of the bill. The expression (2x - 5) represents the length,
which is determined by the value of x, and the expression (5x + 8) represents the width. By substituting different values of x into these expressions, we can find the corresponding dimensions of the Canadian $20 bill.
To know more about length click here
brainly.com/question/30625256
#SPJ11
Two odd numbers are selected at random from integers 11 through 22. Find the
probability that the two numbers are multiples of 3 after replacing first? JUST
SHOW MATH!*
Answers
Probability that the two numbers are multiples of 3 after replacing first
What is Probability?It is a branch of mathematics that deals with the occurrence of a random event.
The odd integers from11 to 22 are
11,13,15,17,19,21
So there are 6 events
Out of these 6 numbers, 2 numbers (15,21) are multiples of 3.
One number out of these 2 numbers can be chosen in 2 ways.
Therefore, favourable number of elementary events = 2.
Required probability =2/6=1/3
Hence 1/3 is the probability that the two numbers are multiples of 3 after replacing first
To learn more on probability click:
https://brainly.com/question/11234923
#SPJ2
test the hypothesis that the mean weight of the two sheets is equal (μ1−μ2)against the alternative that it is not (and assume equal variances). find the t-stat to 3 decimal places.
Answers
To test the hypothesis that the mean weight of two sheets is equal (μ1 - μ2) against the alternative that it is not, and assuming equal variances, we can use a two-sample t-test. The t-statistic can be calculated using the following formula:
t = (x1 - x2) / (s_p * sqrt(1/n1 + 1/n2))
where:
x1 and x2 are the sample means of the two sheets,
s_p is the pooled standard deviation,
n1 and n2 are the sample sizes.
The pooled standard deviation (s_p) can be calculated using the following formula:
s_p = sqrt(((n1 - 1) * s1^2 + (n2 - 1) * s2^2) / (n1 + n2 - 2))
where:
s1 and s2 are the sample standard deviations.
To calculate the t-statistic, we need the sample means, sample standard deviations, and sample sizes.
Once you provide the specific values for these variables, I can assist you in calculating the t-statistic to 3 decimal places.
To learn more about equal variances: -brainly.com/question/30777199
#SPJ11
To test the hypothesis that the mean weight of the two sheets is equal (μ1 - μ2) against the alternative that it is not, we can use a paired t-test assuming equal variances. The paired t-test is used when we have paired data or measurements on the same subjects or objects.
The t-statistic for a paired t-test is calculated as follows:
t = (X1 - X2) / (s / √n)
where X1 and X2 are the sample means of the two samples, s is the pooled standard deviation, and n is the number of pairs.
Please provide the sample means, standard deviation, and sample size for each sheet so that we can calculate the t-statistic to 3 decimal places.
To learn more about equal variances: -brainly.com/question/30777199
#SPJ11
4) Find the surface area of the regular pyramid

Answers
The surface area of the regular pyramid is 131.15 cm.
Define surface area.The surface area is the area occupied by a two-dimensional flat surface. It has a square unit of measurement. The surface area of a three-dimensional object is the space taken up by its outer surface. The whole area of the surface of the specified solid item is referred to as surface area. We should add the areas of the surfaces to determine the object's surface area because the faces of three-dimensional objects are essentially 2D shapes.
Given,
Surface area = 1/2(a× b) + 3/2(b ×s)
Where b is a pyramid's side, a is a triangle's base height, and s is a pyramid's slant height.
Side = 6.1
Base = 7
Slant height = 12
Equating in formula:
1/2(6.1 × 7) + 3/2(6.1 × 12)
1/2(42.7) + 3/2(73.2)
21.35 + 109.8
131.15
The surface area of the regular pyramid is 131.15 cm.
To learn more about surface area, visit:
https://brainly.com/question/2835293
#SPJ13
Tony joined a book club. He received 8 free books when he joined. The table below shows the total number of books, n, he had each month, t, since joining the club. TONY'S CLUB Month (t) Total number of books (n) 0 8 1 11 2 14 3 17 Which equation can be used to find the total number of books, n, Tony will have from the book club after t months?
Answers
The equation that can be used to find the total number of books, n, Tony will have from the book club after t months is C. n = 3t + 8.
What is an equation?An equation is a mathematical statement that two or more algebraic expressions are equal or equivalent.
Equations are depicted using the equal sign (=), unlike mathematical expressions.
In a slope intercept form, the linear equation to find the number of books has is given as n = 3t + 8.
TONY'S CLUB
Month (t) Total number of books (n)
0 8
1 11 (8 + 3)
2 14 (11 + 3)
3 17 (14 + 3)
The initial number of free books Tony when he joined the book club = 8
The additional books Tony receives each month = 3
Let the total number of books received = n
Let the number of months since joining the club = t
n = 3t + 8
For the first month:
n = 3(1) + 8 = 11
For the second month:
n = 3(2) + 8 = 14
For the third month:
n = 3(3) + 8 = 17
Thus, the correction equation is Option C.
Learn more about linear equations at https://brainly.com/question/28732353
#SPJ1
Question Completion:A) n = 8t
B) n = 3t
C) n = 3t + 8
D) n = 8t + 3
THIS IS URGENT please help me
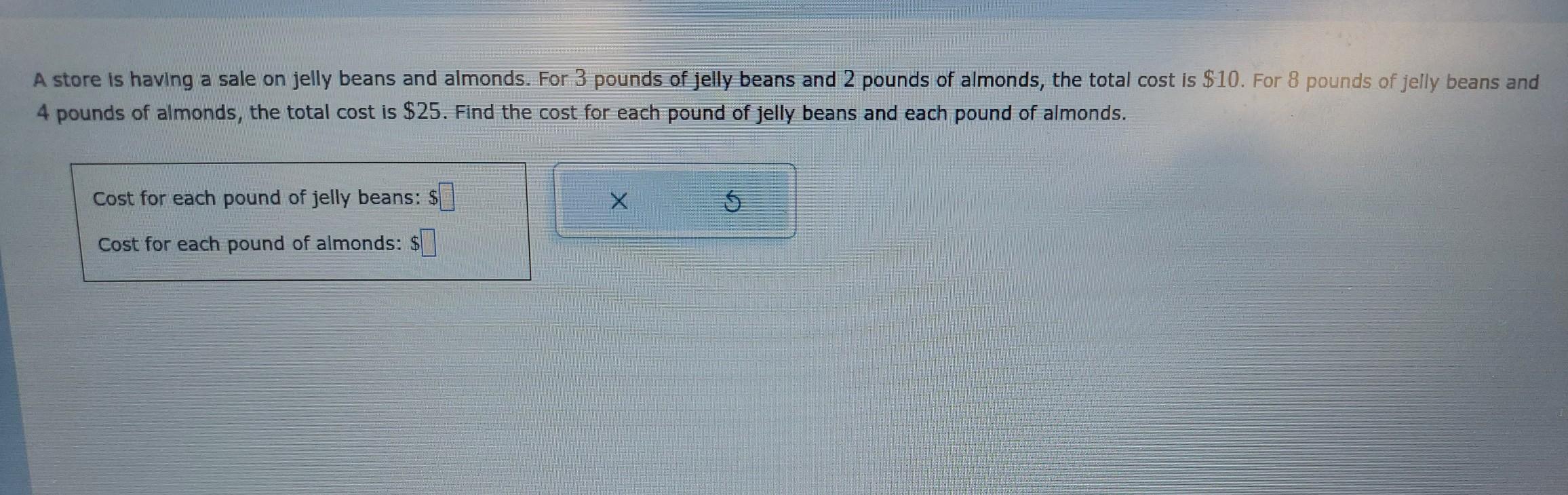
Answers
Answer:
Each pound of jelly beans costs $2.50 and each pound of almonds costs $1.25.
I really struggled while trying to solve this, good luck. (┬┬﹏┬┬)<3
Step-by-step explanation:
2.50*3 = 7.50
1.25*2 = 2.50
7.50 + 2.50 = 10.00
-------------------------------
2.50*8 = 20.00
1.25*4 = 5
20 + 5 = 25
A basketball team scored 8 more points in its second game than in its first. In its third game, the team scored 42 points. The total number of points scored in the three games was more than 150. What is the least number of points the team might have scored in its second game? Will be named brainliest.
Answers
Answer:
58
Step-by-step explanation:
x= points in 2nd game
x+8= points in 1st game
42= points in third game
x+x+8+42>150
2x+50>150
2x>100
Therefore x must be greater than 50.
50+8=58, which is the least amount of points in the second game.