You are a male who has a high school diploma. You plan to attend college and earn a bachelor’s degree. When you graduate from college, you get a job paying $40,780.00/yr. How does your pay once you graduate compare on a monthly basis to the median income degree level you obtained? Your actual earnings are $661.03/month more than the median. Your actual earnings are $605.67/month less than the median. Your actual earnings are $661.03/month less than the median. Your actual earnings are $605.67/month more than the median.
Answers
Answer:
Answer: 11,272
Step-by-step explanation: there are 52 weeks in a year multiplied by the median wage, which is 1001. Then minus 40,780.
Step-by-step explanation:
HOPE THIS HELPS!!!!!! :D
Related Questions
what do you add to 5 8/9 to make 7
Answers
2(5x + 2) = 10x - 4
what is the x
Answers
Answer:umm
There are no values of
x
that make the equation true.
No solution
Step-by-step explanation:
Find the H.C.F. of 567 and 255 using Euclid’s division lemma.
Answers
Step-by-step explanation:
To find the Highest Common Factor (H.C.F.) of 567 and 255 using Euclid's division lemma, we can follow these steps:
Step 1: Apply Euclid's division lemma:
Divide the larger number, 567, by the smaller number, 255, and find the remainder.
567 ÷ 255 = 2 remainder 57
Step 2: Apply Euclid's division lemma again:
Now, divide the previous divisor, 255, by the remainder, 57, and find the new remainder.
255 ÷ 57 = 4 remainder 27
Step 3: Repeat the process:
Next, divide the previous divisor, 57, by the remainder, 27, and find the new remainder.
57 ÷ 27 = 2 remainder 3
Step 4: Continue until we obtain a remainder of 0:
Now, divide the previous divisor, 27, by the remainder, 3, and find the new remainder.
27 ÷ 3 = 9 remainder 0
Since we have obtained a remainder of 0, the process ends here.
Step 5: The H.C.F. is the last non-zero remainder:
The H.C.F. of 567 and 255 is the last non-zero remainder obtained in the previous step, which is 3.
Therefore, the H.C.F. of 567 and 255 is 3.
Determine the equation of the parabola with focus
(
2
,
5
)
(2,5) and directrix
�
=
18
x=18.
Answers
The equation of the parabola with focus (2,5) and directrix x=18 is (x - 18)² + (y - 5)² = (y - (5 + (18 - 2) / 2))².
A parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating
straight line of that surface.
The focus of a parabola is a fixed point on the interior of a parabola used in the formal definition of the curve.
The directrix is a straight line perpendicular to the axis of symmetry and placed symmetrically with respect to the focus.
The axis of symmetry is the line through the focus and perpendicular to the directrix.
The vertex of a parabola is the point where its axis of symmetry intersects the curve. It is the point where the parabola changes direction or "opens
up" or "opens down.
The directrix is a fixed straight line used in the definition of a
parabola. It is placed such that it is perpendicular to the axis of symmetry and at a distance from the vertex equal to the
distance between the vertex and focus. It is the line that is equidistant to the focus and every point on the curve.Here's
the solution to the given problem:
The distance between the directrix and the focus is equal to p = 16 (since the directrix is x = 18, the parabola opens to the left, so the distance is measured horizontally)
The vertex is (h,k) = ((18+2)/2,5) = (10,5)
Then we can use the following formula: (x - h)² = 4p(y - k)
Substitute the vertex and the value of p. (x - 10)² = 64(y - 5)
Expand and simplify. (x - 10)² + (y - 5)² = 64(y - 5)
The equation of the parabola is (x - 10)² + (y - 5)² = 64(y - 5).
for such more question on parabola
https://brainly.com/question/17987697
#SPJ11
find the value of y and the size of the angle in the triangle 3y,y,4y-4
Answers
The value of y is given as follows:
y = 23.
Hence the angle measures are given as follows:
69º, 23º and 88º.
How to obtain the measures?The sum of the measures of the internal angles of a triangle is of 180º.
The internal angles for the triangle in this problem have the measures given as follows:
3y.y.4y - 4.Hence the value of y is obtained as follows:
3y + y + 4y - 4 = 180
8y = 184
y = 184/8
y = 23.
Hence the angle measures are given as follows:
3y = 3 x 23 = 69º.y = 23º.4y - 4 = 4(23) - 4 = 88º.More can be learned about angle measures at https://brainly.com/question/24607467
#SPJ1
a very anti-social species of fish will be harvested at a constant rate h. the intrinsic growth rate for the fish population is. write the differential equation to model the growth rate for the fish population with harvesting
Answers
The logistic model shows how the growth of a population is limited by its environment.
The differential equation that models the growth rate for the fish population with harvesting when a very anti-social species of fish will be harvested at a constant rate h and the intrinsic growth rate for the fish population is is given below:$$\frac{dN}{dt}= rN - hN$$Where N is the population of fish, t is time, r is the intrinsic growth rate, and h is the rate of harvesting. The first term in the above equation represents the population growth rate, and the second term represents the population loss rate due to harvesting. The differential equation is also known as a logistic model or Verhulst model. The logistic model, on the other hand, takes into account limiting factors such as the population size and resources available.
Learn more about Growth rate
brainly.com/question/13870574
#SPJ11
limx->3- -5x^2+1/x-3
Answers
Answer: ∞
Step-by-step explanation:
\(\displaystyle\\ \lim_{x \to 3-0} \frac{-5x^2+1}{x-3} =\\\\ \frac{-5(3-0)^2+1}{3-0-3} =\\\\\frac{-5(3)^2+1}{-0}=\\\\\frac{-5(9)+1}{-0}=\\\\\frac{-45+1}{-0} =\\\\\frac{-44}{-0} =\\\\\frac{44}{0} =\\\\\infty\)
There are 400 counters in a box.
The counters are red or yellow or green.
3
of the counters are red.
82 of the counters are yellow.
What percentage of the counters are green?
Answers
the green would be 15% of the counters
The number of counters that are green is 162 and the percentage of counters that are green is 42 %
What is an Equation?
Equations are mathematical statements with two algebraic expressions flanking the equals (=) sign on either side.
It demonstrates the equality of the relationship between the expressions printed on the left and right sides.
Coefficients, variables, operators, constants, terms, expressions, and the equal to sign are some of the components of an equation. The "=" sign and terms on both sides must always be present when writing an equation.
Given data ,
The total number of counters = 400
The number of counters that are red = 3/8 of total number of counters
= ( 3/8 ) x 400
= 3 x 50
= 150 counters
The number of counters that are yellow = 82 counters
So , the number of counters that are green =
Total number of counters - number of counters that are red - number of counters that are yellow
The number of counters that are green = 400 - 150 - 82
= 168 counters
Now , the percentage of counters that are green =
( number of counters that are green / total number of counters ) x 100
The percentage of counters that are green = ( 168 / 400 ) x 100
= 168 / 4
= 42 %
Hence , the number of counters that are green is 168 and the percentage of counters that are green is 42 %
To learn more about equations click :
https://brainly.com/question/10413253
#SPJ2
Suppose that X has a hypergeometric distribution with N = 100, n = 4, and K = 20. Determine the following: a. P(X = 1) b. P(X = 6) c. P(X = 4) d.
Answers
The probabilities for the hypergeometric distribution with the given parameters are:
a. P(X = 1) ≈ 0.000407
b. P(X = 6) = 0
c. P(X = 4) ≈ 0.098117
d. P(X = 0) ≈ 1.97e-05
What is probability?Probability is a measure of the likelihood of an event to occur. Many events cannot be predicted with total certainty.
To determine the probabilities for the hypergeometric distribution with the given parameters, we can use the following formula:
P(X = k) = (choose(K, k) * choose(N-K, n-k)) / choose(N, n)
where "choose(a, b)" represents the binomial coefficient, calculated as a! / (b! * (a - b)!)
Let's calculate the probabilities:
a. P(X = 1):
P(X = 1) = (choose(20, 1) * choose(100-20, 4-1)) / choose(100, 4)
= (20 * 80) / 3921225
≈ 0.000407
b. P(X = 6):
P(X = 6) = (choose(20, 6) * choose(100-20, 4-6)) / choose(100, 4)
= (38760 * 0) / 3921225
= 0
c. P(X = 4):
P(X = 4) = (choose(20, 4) * choose(100-20, 4-4)) / choose(100, 4)
= (4845 * 80) / 3921225
≈ 0.098117
d. P(X = 0):
P(X = 0) = (choose(20, 0) * choose(100-20, 4-0)) / choose(100, 4)
= (1 * 77) / 3921225
≈ 1.97e-05
Therefore:
a. P(X = 1) ≈ 0.000407
b. P(X = 6) = 0
c. P(X = 4) ≈ 0.098117
d. P(X = 0) ≈ 1.97e-05
Learn more about probability on:
https://brainly.com/question/13604758
#SPJ4
The complete question is:
Suppose that X has a hypergeometric distribution with N = 100, n = 4, and K = 20. Determine the following: a. P(X = 1) b. P(X = 6) c. P(X = 4) d. P(X = 0).
Hudson bought snacks for his team's practice. he bought a bag of apples for $1.59 and a 10-pack of juice bottles. the total cost before tax was $7.39. write and solve an equation which can be used to determine xx, how much each bottle of juice cost
Answers
The cost of each bottle of juice will be $0.58.
What is an expression?The mathematical expression combines numerical variables and operations denoted by addition, subtraction, multiplication, and division signs.
Mathematical symbols can be used to represent numbers (constants), variables, operations, functions, brackets, punctuation, and grouping. They can also denote the logical syntax's operation order and other properties.
Given that Hudson bought snacks for his team's practice. he bought a bag of apples for $1.59 and a 10-pack of juice bottles. the total cost before tax was $7.39.
The expression will be formed as below:-
10x + 1.59 = 7.39
Here x is the cost of the juice bottle.
10x + 1.59 = 7.39
10x = 7.39 - 1.59
10x =5.8
x = 5.8/10 = $0.58
Therefore, the cost of each bottle of juice will be $0.58.
To know more about an expression follow
https://brainly.com/question/28306908
#SPJ1
Help pls. Stuck on Khan Academy question in High School Geometry


Answers
Answer:
A
Step-by-step explanation:
Sequence A works.
With sequence B, the triangles will be next to each other.
Answer: A
apply the distributive property to write an equivalent expression
4(2+w)
Answers
Hi there I so need your help with this question 5 x - 2 - (8 - 12) + 16 / - 8 = please help if u did, your the best!! :) I am sure I will help with your question someday too.
Answers
Answer:
5x
Step-by-step explanation:
Reformatting the input :
Changes made to your input should not affect the solution:
(1): "/-8" was replaced by "/(-8)".
STEP 1 :
Simplify 2/-1
Equation at the end of step 1 :
(5x + 2) + -2
Final result :
5x
F(x)=e*1/x
Calculate f'(x)
Answers
Answer:
\(\huge\boxed{f'(x)=-\dfrac{e^\frac{1}{x}}{x^2}}\)
Step-by-step explanation:
\((e^x)'=e^x\\\\\bigg[f\bigg(g(x)\bigg)\bigg]'=f'\bigg(g(x)\bigg)\cdot g'(x)\\\\\left(\dfrac{1}{x}\right)'=-\dfrac{1}{x^2}\\\\====================\)
\(f(x)=e^\frac{1}{x}=\left(e^\frac{1}{x}\right)'\cdot\left(\dfrac{1}{x}\right)'=e^\frac{1}{x}\cdot\left(-\dfrac{1}{x^2}\right)=-\dfrac{e^\frac{1}{x}}{x^2}\)
the positive integers and form an arithmetic sequence while the integers and form a geometric sequence. if what is the smallest possible value of ?
Answers
To solve this problem, we need to use the formulas for arithmetic and geometric sequences. The smallest possible value of n is 1 or 3 .
For the arithmetic sequence, we have a common difference of d = 2 (since we are adding 2 to each term to get the next term). So we can write the nth term as an = a1 + (n-1)d, where a1 = 1 is the first term.
For the geometric sequence, we have a common ratio of r = 3 (since we are multiplying each term by 3 to get the next term). So we can write the nth term as gn = g1 * r^(n-1), where g1 = 3 is the first term.
We want to find the smallest value of n such that an = gn. So we set the two formulas equal to each other and solve for n:
a1 + (n-1)d = g1 * r^(n-1)
1 + (n-1)2 = 3^(n-1)
Simplifying the right-hand side, we get:
1 + 2n - 2 = 3^(n-1)
2n - 1 = 3^(n-1)
We can solve this equation by trial and error. For n = 1, the left-hand side is 1 and the right-hand side is 1, so n=1 is a solution. For n=2, the left-hand side is 3 and the right-hand side is 2, so n=2 is not a solution. For n=3, the left-hand side is 5 and the right-hand side is 5, so n=3 is a solution.
Therefore, the smallest possible value of n is 1 or 3. We can check that both of these values work:
a1 + (n-1)d = 1 + 0*2 = 1
g1 * r^(n-1) = 3 * 3^(0) = 3
and
a1 + (n-1)d = 1 + 2*2 = 5
g1 * r^(n-1) = 3 * 3^(2) = 27
So the answer is n = 1 or 3.
To know more about Arithmetic visit :
https://brainly.com/question/16415816
#SPJ11
PLEASE HELP ME SOLVE THIS!

Answers
The sine function for this problem is given as follows:
y = 3sin(2x) + 1.
How to define a sine function?The standard definition of the sine function is given as follows:
y = Asin(B(x - C)) + D.
For which the parameters are given as follows:
A: amplitude.B: the period is 2π/B.C: phase shift.D: vertical shift.The function oscillates between -2 and 4, for a difference of six, hence the amplitude is given as follows:
2A = 6
A = 3.
The midline is then given as follows:
y = (-2 + 4)/2
y = 1.
The function oscillates between -A + 1 and A + 1, hence the vertical shift is given as follows:
D = 1.
The period is of 5π/4 - π/4 = π units, hence the coefficient B is given as follows:
2π/B = π
B = 2.
The function is at it's midline when x = 0, hence it has no phase shift and is given as follows:
y = 3sin(2x) + 1.
More can be learned about trigonometric functions at brainly.com/question/21558626
#SPJ1
Verify each identity. sin²(θ + π/2 ) = -con²θ
Answers
To verify the identity sin²(θ + π/2) = -cos²θ, we'll use trigonometric identities and algebraic manipulations:
Starting with the left-hand side (LHS):
sin²(θ + π/2)
We'll apply the sum-to-product formula for sine:
sin(A + B) = sin(A)cos(B) + cos(A)sin(B)
sin(θ + π/2) = sin(θ)cos(π/2) + cos(θ)sin(π/2)
Since cos(π/2) = 0 and sin(π/2) = 1:
sin(θ + π/2) = sin(θ) * 0 + cos(θ) * 1
sin(θ + π/2) = cos(θ)
Now let's simplify the right-hand side (RHS):
-cos²θ
We'll use the identity cos²θ = 1 - sin²θ:
-cos²θ = - (1 - sin²θ)
Expanding the negative sign:
-cos²θ = -1 + sin²θ
Now, comparing the LHS and RHS, we have:
sin(θ + π/2) = cos(θ)
and
-cos²θ = -1 + sin²θ
Both expressions are equivalent, so the identity sin²(θ + π/2) = -cos²θ is verified.
Learn more about Trigonometry here:
https://brainly.com/question/12068045
#SPJ11
PLEAASE HALLP EXPLAIN!! NEED HEEELP 14 POINTS

Answers
Hope this helps and Happy Friday!

4.1 & 4.2 Review
1. Write an equation of the line with a slope of and a y-intercept of -8.
Answers
Find the lateral surface area of the figure.
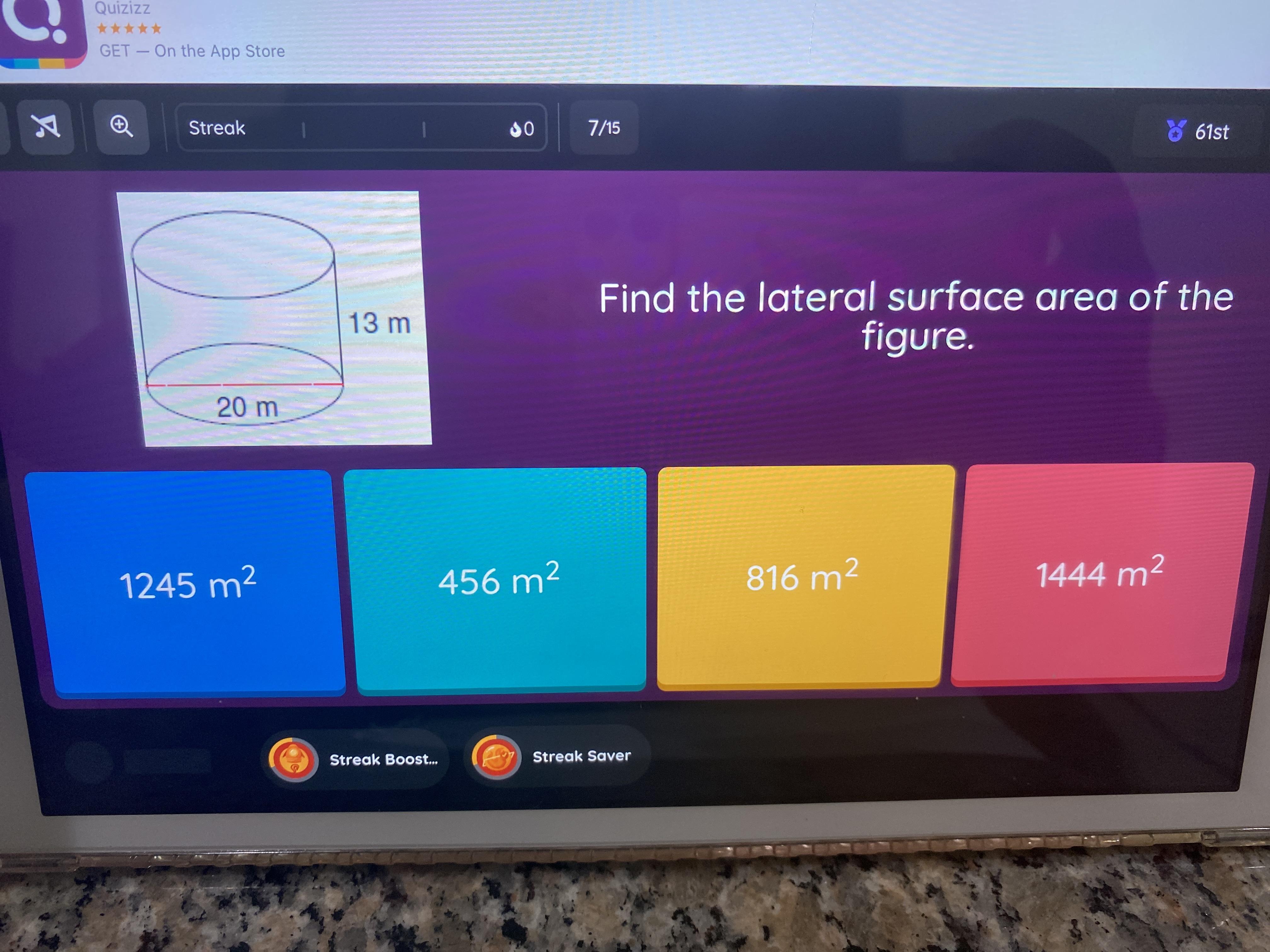
Answers
The evaluated lateral surface area is 261.8 square meters, under the condition that the base length is 20 m and height is 13 m.
The lateral surface area of a cylinder is given by the formula 2πrh
Here,
r = radius of the base
h = height of the cylinder.
For the given case, the base length is 20 m and height is 13 m. Then the base length is stated instead of the radius, we have to evaluate the radius first.
The radius of a cylinder can be found applying the formula r = l/2π
Here,
l = base length.
So, staging l = 20 m
, we get
r = 20/(2π)
≈ 3.18 m
Now that we have received the radius and height, we can evaluate the lateral surface area applying the formula mentioned above.
Staging
r = 3.18 m
h = 13 m,
we get:
Lateral surface area
= 2πrh
≈ 261.8 m²
Then, the lateral surface area of the given cylinder is approximately 261.8 square meters.
To learn more about surface area
https://brainly.com/question/951562
#SPJ1
Can i Some More hELp??? i will give brainliest!!!!

Answers
Answer:
c
Step-by-step explanation:
PLEASE ANSWER THIS
imagine is above
Figure 3 shows the electronic structure of an atom.
Figure 3
Electron
Nucleus
RON
This element is in the shaded group on Figure 2.
Why is this element unreactive?

Answers
Answer:
huh looks simple....it's unreactive because it's already stable
Step-by-step explanation:
it has eight electrons in the outer most energy level making it stable so it doesn't need to loose or gain electrons
18+17+16+15+14+13+12+11+10 what is the answer
Answers
126
Jalen has a scale model of a train. 2 centimeters in the represents 3 feet in real train.
The height of the model train is 10.2 centimeters.
What is the real height of the real train??
Answers
Answer: 15.3feet
Step-by-step explanation: Given the scale model of a train as;2cm = 3feet
We are to find the height of real train of height 10.2cm, we can write; 10.2cm = xDivide both expressions
2/10.2 = 3/x2x = 3×10.22x = 30.6x= 15.3
Hence the height if the real train is 15.3feet
The real height of the real train will be;
⇒ 15.3 feet
What is Measurement unit?
A measurement unit is a standard quality used to express a physical quantity. Also it refers to the comparison between the unknown quantity with the known quantity.
Given that;
Jalen has a scale model of a train. 2 centimeters in the represents 3 feet in real train.
Now,
Since, Jalen has a scale model of a train. 2 centimeters in the represents 3 feet in real train.
And, The height of the model train is 10.2 centimeters.
Hence, In the scale model;
1 centimeter = 3/2 feet
Thus, We get;
10.2 centimeters = 10.2 × 3/2 feet
= 5.1 × 3 feet
= 15.3 feet
Therefore, The real height of the real train will be;
⇒ 15.3 feet
Learn more about the measurement unit visit:
https://brainly.com/question/777464
#SPJ2
What is the range of the points on the graph?

Answers
Answer:16
Step-by-step explanation:
The table below shows how much time some people spent exercising yesterday. a) What is the modal class of time spent exercising? b) In which class does the median lie? Time spent, x (minutes) 0≤x≤10 10< x≤20 20< x≤30 30< x≤40 40< x≤50 50≤x≤60 Frequency 18 14 3 16 21 7
Answers
a) The modal class of time spent exercising is given as follows: 40 < x ≤ 50
b) The median lies on the class 30 < x ≤ 40.
How to obtain the median and mode?The mode of a data-set is the observation that appears the most times in the data-set, hence, for item a, we consider that the mode lies in the class 40 < x ≤ 50, which has the highest number of observations, which is 21.
The total number of elements in the data-set is given as follows:
18 + 14 + 3 + 16 + 21 + 7 = 79.
Hence the median is the element at the cumulative position given as follows:
(79 + 1)/2 = 40.
Which is on the following class:
30 < x ≤ 40.
More can be learned about median and mode at https://brainly.com/question/14532771
#SPJ1
The eccentricity of the conic section below is
A. Closer to 0 than 1
B. Closer to 1 then 0

Answers
The eccentricity of the conic section below is: A. closer to 0 than 1.
What is a conic section?In Euclidean geometry, a conic section can be defined as a curve that is generated as the intersection of the surface of a right circular cone with a plane.
In Mathematics, there are four (4) types of conic section and these include the following with their eccentricity:
Hyperbola: its eccentricity is greater than one (1).Parabola: its eccentricity is equal to one (1).Ellipse: its eccentricity is 0 < e < 1.Circle: its eccentricity is equal to zero (0).In this context, we can reasonably infer and logically deduce that the eccentricity of the conic section is closer to zero (0) than one (1) because it represents a circle.
Read more on conic section here: https://brainly.com/question/4017703
#SPJ1
A rectangle has a length of 25 feet and a width of 18 feet what is the area model of the rectangle
Answers
Answer:
450 sq.feet
Step-by-step explanation:
Given,
Length ( l ) = 25 feet
Width ( b ) = 18 feet
To find :
Area ( rectangle ) = ?
Formula : -
Area ( rectangle ) = l x b
Area ( rectangle )
= 25 x 18
= 450 sq.feet
Check photo for work
solve for m - hp = d for p
please actually help this is my first assignment of the year and can’t fail
Answers
m - hp = d
-hp = d - m.
Then, all we have to do is isolate the “p” variable:
p = -(d - m) / h
p = ( -d + m ) / h
* You have a dog that can run 5 km/hr. How fast can she run in mi/hr? (i.e. convert the rate to miles per hour) (1.6 km=1mi) DO NOT JUST TYPE THIS INTO A CONVERTER ONLINE. YOU WILL NOT GET THE ANSWER RIGHT. Express your answer as decimal, rounded to the nearest thousandth (three decimal places) in mi/hr - no spaces EXAMPLE: 78.345mi/hr
Answers
The dog's running speed of 5 km/hr can be converted to approximately 3.125 mi/hr by multiplying it by the conversion factor of 1 mi/1.6 km. Rounding to the nearest thousandth, the dog can run at about 3.125 mi/hr.
To convert the dog's running speed from kilometers per hour (km/hr) to miles per hour (mi/hr), we need to use the conversion factor of 1.6 km = 1 mi.First, we can convert the dog's speed from km/hr to mi/hr by multiplying it by the conversion factor: 5 km/hr * (1 mi/1.6 km) = 3.125 mi/hr.
However, we need to round the answer to the nearest thousandth (three decimal places). Since the digit after the thousandth place is 5, we round up the thousandth place to obtain the final answer.
Therefore, the dog can run at approximately 3.125 mi/hr.
To learn more about factor click here
brainly.com/question/26923098
#SPJ11