y = -2x - 5
6x + 3y = -15
A.one line
B.parallel lines
C.intersecting lines
Answers
Answer:
A. One line
Step-by-step explanation:
Let rearrange the system of equations into explicit forms:
\(y = -2\cdot x - 5\)
\(6\cdot x + 3\cdot y = -15\)
\(3\cdot y = -6\cdot x - 15\)
\(y = -2\cdot x - 5\)
The second equation is identical to the first one, which means that there is just one line.
Related Questions
how do you simplify algebraic expressions
Answers
You have five student groups to present in class one group cannot go first because they need additional set up time and how many orders can they present
Answers
They can present in 96 different orders. Given, there are five student groups to present in class and one group cannot go first because they need additional set-up time.
Permutation is to select an object then arrange it and it cares about the orders while Combination is about only selecting an object without caring the orders.
We have 5 positions to fill here.
First position: 4 ways (one of the rest 4 groups will present first)
Second position: 4 ways (one of the rest 3 groups and the group which could not present first, will present second)
Third position: 3 ways (one of the rest 3 groups will present third)
Fourth position: 2 ways (one of the rest 2 groups will present fourth)
Fifth position: 1 way (rest group will present last)
Total ways in which they can present = 4*4*3*2*1 = 96
Hence, the answer is 96.
Learn more about permutation at:
https://brainly.com/question/28065038
#SPJ4
what is polynomial name of 5 - 9y
Answers
Answer:
Question For You
Question 1: Identify the Monomial, Binomial, Trinomial, Polynomial, and Multinomial from the following:
a) 5pq b) 3b + 5c
c) x + y + z d) a2+ 2b
Answer : a) Monomial b) Polynomial
c) Trinomial d) Binomial
Solve for X
4(5x+6)=12
-3(2x-4)=18
26=2(3x-2)
Answers
The value of x in the equations are:
1. x = -3/5
2. x = -1
3. x = 5
How to Solve an Equation?Given the equations above, to solve for x, isolate x as the variable in the equation to one side of the equation.
a. 4(5x+6) = 12
Apply the distributive property
20x + 24 = 12
20x = 12 - 24
20x = -12
x = -12/20
x = -3/5
b. -3(2x - 4) = 18
Apply the distributive property
-6x + 12 = 18
-6x + 12 - 12 = 18 - 12
-6x = 6
x = 6/-6
x = -1
c. 26 = 2(3x - 2)
Apply the distributive property
26 = 6x - 4
26 + 4 = 6x
30 = 6x
5 = x
x = 5
Learn more about equations on:
https://brainly.com/question/25678139
#SPJ1
In ΔRST, the measure of ∠T=90°, the measure of ∠R=67°, and TR = 94 feet. Find the length of RS to the nearest tenth of a foot.
Answers
Answer:
the length of RS to the nearest tenth of a foot is 240.6ft

solve
3x-11x-20=0.
.
Answers
Answer: x=-5/2
Step-by-step explanation:
1.add similar elements
-8x-20=0
2.add 20 to both sides
-8x-20+20=0+20
3.simplify
-8x=20
4. divide both sides by -8
-8x/-8 = 20/-8
5.simplify
x=-5/2
a. What is the probability that a randomly selected survey participant prefers the NFL? 0.5286 (Round to four decimal places as needed.) b. What is the probability that a randomly selected survey participant has a college degree and prefers the NBA? (Round to four decimal places as needed.) a. Of two customers selected, what is the probability that both will be on a business trip? 0.1719 (Round to four decimal places as needed.) b. What is the probability that a customer will be on a business trip or will experience a hotel problem during a stay at the hotel? (Round to four decimal places as needed.)
Answers
a. The probability that a randomly selected survey participant prefers the NFL is given as 0.5286. This means that out of all the participants in the survey, approximately 52.86% indicated a preference for the NFL.
b. To determine the probability that a randomly selected survey participant has a college degree and prefers the NBA, we would need additional information about the joint probability of these events. Without that information, we cannot calculate the exact probability.
a. To find the probability that both of two randomly selected customers will be on a business trip, we need to know the individual probabilities of each customer being on a business trip and assume that their trips are independent. If the probability of customer A being on a business trip is denoted as P(A) and the probability of customer B being on a business trip is denoted as P(B), then the probability of both being on a business trip is given by P(A and B) = P(A) * P(B). The given probability of 0.1719 may represent this joint probability.
b. The probability that a customer will be on a business trip or will experience a hotel problem during a stay at the hotel can be determined by summing the individual probabilities of these events. Let's denote the probability of being on a business trip as P(B) and the probability of experiencing a hotel problem as P(H). Then, the probability of either event occurring can be calculated as P(B or H) = P(B) + P(H) - P(B and H), assuming that the events are mutually exclusive. However, the specific values of P(B), P(H), and P(B and H) are needed to compute the exact probability.
Learn more about probability here:
https://brainly.com/question/31828911
#SPJ11
Find the solutions of the equation.
23 <3x-3(-) ≤ 66
a) (-, 11)u[33, [infinity])
b)(-, 11]u[33,[infinity])
c) (11,33)
d) [11, 33]
e) (11, 33]
f) None of the above.
Answers
The solution to the inequality is:
x ∈ (-∞, -21].
The correct option is F.
To solve the given inequality, we'll first simplify the expression:
23 < 3x - 3 ≤ -66
To simplify the inequality,
23 < 3x - 3 ≤ -66
Adding 3 to all parts of the inequality:
23 + 3 < 3x - 3 + 3 ≤ -66 + 3
Simplifying:
26 < 3x ≤ -63
Next, divide all parts of the inequality by 3:
26/3 < 3x/3 ≤ -63/3
Simplifying:
8.67 < x ≤ -21
Therefore, the solution to the inequality is:
x ∈ (-∞, -21]
Learn more about Inequality here:
https://brainly.com/question/20383699
#SPJ4
the absolute value of a number is 55 select all the integers that this number could be
Answers
Answer:
-55 and 55Step-by-step explanation:
Let the number be x:
|x| = 55x = ± 55So absolute value of -55 and 55 is 55
Answer:
\( | - 55| = 55 \)
Absolute value of both 55 and |-55| is 55.
a study is conducted to determine if one can predict the yield of a crop based on the amount of yearly rainfall. the response variable in this study is:
Answers
The response variable in this study is the yield of the crop, as it is the variable that is being measured to see if it is affected by the amount of rainfall.
The choice of a response variable in a statistical study:
In a statistical study, the response variable is the variable of interest that is being measured or observed. It is the outcome that we want to understand, predict, or explain.
The response variable can be a numerical quantity, such as height, weight, temperature, or yield, or it can be a categorical variable, such as gender, species, color, or rating.
The choice of a response variable is crucial in a statistical study, as it determines the research question and the type of analysis that will be used.
In the given study, the researchers are trying to determine whether there is a relationship between two variables: the amount of rainfall and the yield of the crop.
The amount of rainfall is the independent variable, as it is the variable that is being manipulated (or measured) to see if it has an effect on the dependent variable, which is the yield of the crop.
Therefore,
The response variable in this study is the yield of the crop, as it is the variable that is being measured to see if it is affected by the amount of rainfall.
Learn more about Response variable at
https://brainly.com/question/30332171
#SPJ4
Q3 Estimate the monthly average daily radiation on a horizontal surface \( \mathrm{H} \) in June in Amman given the following : Monthly average hours per day of sunshine in June 10 hours Climate type:
Answers
The estimated monthly average daily radiation on a horizontal surface in June in Amman is approximately 7.35 kWh/m(^2)/day.
To estimate the monthly average daily radiation on a horizontal surface H in June in Amman, we can use the following equation:
\([H = S \times H_s \times \frac{\sin(\phi)\sin(\delta)+\cos(\phi)\cos(\delta)\cos(H_a)}{\pi}]\)
where:
S is the solar constant, which is approximately equal to 1367 W/m(^2);
\(H(_s)\) is the average number of sunshine hours per day in Amman in June, which is given as 10 hours;
(\(\phi\)) is the latitude of the location, which for Amman is approximately 31.9 degrees North;
(\(\delta\)) is the solar declination angle, which is a function of the day of the year and can be calculated using various methods such as the one given in the answer to Q1;
\(H(_a)\) is the hour angle, which is the difference between the local solar time and solar noon, and can also be calculated using various methods such as the one given in the answer to Q1.
Substituting the given values, we get:
\([H = 1367 \times 10 \times \frac{\sin(31.9)\sin(\delta)+\cos(31.9)\cos(\delta)\cos(H_a)}{\pi}]\)
Since we are only interested in the monthly average daily radiation, we can assume an average value for the solar declination angle and the hour angle over the month of June. For simplicity, we can assume that the solar declination angle (\(\delta\)) is constant at the value it has on June 21, which is approximately 23.5 degrees North. We can also assume that the hour angle \(H(_a)\) varies linearly from -15 degrees at sunrise to +15 degrees at sunset, with an average value of 0 degrees over the day.
Substituting these values, we get:
\([H = 1367 \times 10 \times \frac{\sin(31.9)\sin(23.5)+\cos(31.9)\cos(23.5)\cos(0)}{\pi}]\)
Simplifying the equation, we get:
\([H \approx 7.35 \text{ kWh/m}^2\text{/day}]\)
Therefore, the estimated monthly average daily radiation on a horizontal surface in June in Amman is approximately 7.35 kWh/m(^2)/day.
Learn more about "average daily radiation " : https://brainly.com/question/32911494
#SPJ11
Please its really urgent, step by step working out
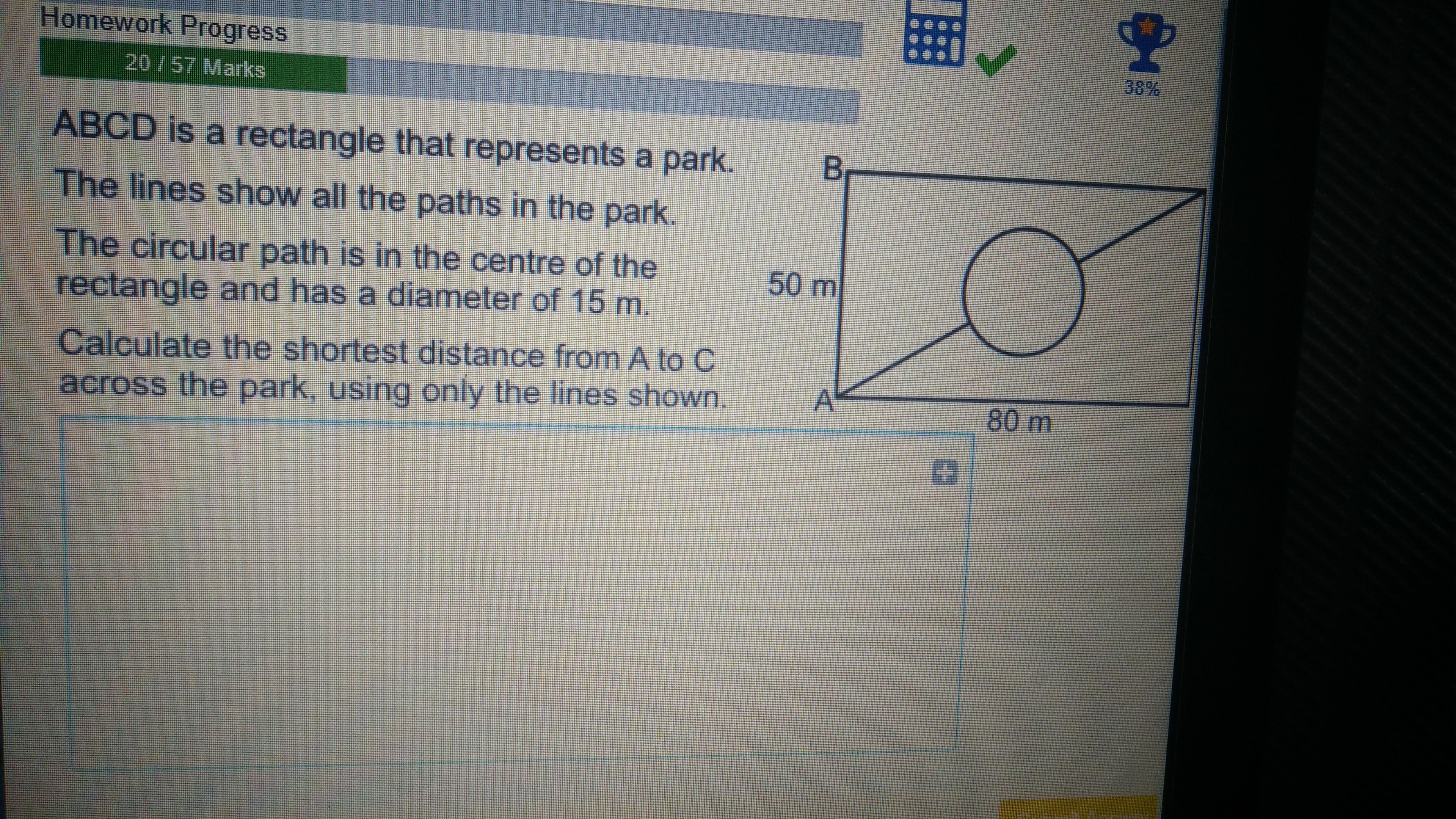
Answers
Answer:
70.99
Step-by-step explanation:
Use Pythagorean Theorem to find the shortest distance.
80^2-50^2=3900
Square rt= 62.44
Subtract by 15
47.44
Next find half of the circular path it is (3.14 x 15)/2
23.55
Add 47.44+23.55=70.99
Hope this is correct
Draw a line representing the "rise" and a line representing the "run" of the line. State the slope of the line in simplest form.

Answers
Answer:
\(\frac{4}{5}\)
Step-by-step explanation:

The drama club is selling tickets to their play to raise money for the show's expenses. Each student ticket sells for $6.50 and each adult ticket sells for $11.50. The drama club must make a minimum of $1300 from ticket sales to cover the show's costs. Write an inequality that could represent the possible values for the number of student tickets sold, ss, and the number of adult tickets sold, aa, that would satisfy the constraint.
Answers
The inequality that could represent the possible values for the number of tickets sold will be 6.5s + 11.5a ≥ 1300.
What is inequality?Inequality is defined as an equation that does not contain an equal sign. Inequality is a term that describes a statement's relative size and can be used to compare these two claims.
The dramatization club is offering passes to their play to fund-raise for the show's costs. Every understudy ticket sells for $6.50 and every grown-up ticket sells for $11.50. The dramatization club should make at least $1300 from ticket deals to take care of the show's expenses.
Let 's' and 'a' be the number of tickets sold to students and adults, respectively. Then the inequality is given as,
6.5s + 11.5a ≥ 1300
The inequality that could represent the possible values for the number of tickets sold will be 6.5s + 11.5a ≥ 1300.
More about the inequality link is given below.
https://brainly.com/question/19491153
#SPJ1
Let L : R2→R 2 be a LT such that L(x, y) = (x+y, 2x-y). Find
the:
(a.) ker(L)
(b.) range(L)
Show if L is: (c.) one-to-one , (d.) onto
Answers
(a) To find the kernel (ker) of L, we need to find the vectors (x, y) in R^2 such that L(x, y) = (0, 0).
Setting up the equations:
x + y = 0
2x - y = 0
Solving these equations, we find:
x = 0
y = 0
Therefore, the kernel of L is the zero vector, ker(L) = {(0, 0)}.
(b) To find the range of L, we need to determine the set of all possible outputs (x', y') such that there exists (x, y) in R^2 satisfying L(x, y) = (x', y').
Using L(x, y) = (x + y, 2x - y), we can see that any vector (x', y') in R^2 can be written as:
x' = x + y
y' = 2x - y
Simplifying the equations, we find:
x = (x' + y')/3
y = (2x' - y')/3
Therefore, the range of L is the set of all vectors (x', y') in R^2.
(c) To determine if L is one-to-one (injective), we need to check if different inputs map to different outputs.
Let (x₁, y₁) and (x₂, y₂) be two vectors in R^2 such that L(x₁, y₁) = L(x₂, y₂). Then we have:
(x₁ + y₁, 2x₁ - y₁) = (x₂ + y₂, 2x₂ - y₂)
This implies the following system of equations:
x₁ + y₁ = x₂ + y₂
2x₁ - y₁ = 2x₂ - y₂
Simplifying the equations, we find:
x₁ - x₂ = y₂ - y₁
From this equation, we can see that the only solution is x₁ = x₂ and y₁ = y₂.
Therefore, L is one-to-one (injective).
(d) To determine if L is onto (surjective), we need to check if every vector in the codomain (R^2) has a pre-image in the domain (R^2).
Let (x', y') be an arbitrary vector in R^2. We need to find (x, y) in R^2 such that L(x, y) = (x', y').
From the equations obtained in part (b), we have:
x = (x' + y')/3
y = (2x' - y')/3
These equations provide a solution for any (x', y') in R^2.
Therefore, L is onto (surjective).
In summary:
(a) ker(L) = {(0, 0)}
(b) range(L) = R^2
(c) L is one-to-one (injective)
(d) L is onto (surjective)
Learn more about equations here:
https://brainly.com/question/29657983
#SPJ11
we roll two six-sided fair dice. list all the outcomes that the sum of the numbers showing face up is at least 9. what is the probability of the event that the sum of the numbers showing face up is at least 9?
Answers
the probability of the event that the sum of the numbers showing face up is at least 9 is 1/9.
What is probability?
The chance of an event can be calculated using the probability formula by simply dividing the favourable number of possibilities by the total number of outcomes. The likelihood of an event occurring can be anything between 0 and 1, as the favourable number of outcomes can never exceed the total number of outcomes.
Rolling two dice produces a total of 36 possible results.
One of the following will be necessary to reach the amount of 9: (3,6),(6,3),(4,5), or (5,4). 4 final results out of 36 overall.
Rolling two dice results in a 4/36 or 1/9 chance of having a sum of nine.
Hence the probability of the event that the sum of the numbers showing face up is at least 9 is 1/9.
Learn more about probability, by the following link.
brainly.com/question/24756209
#SPJ4
Find the area of this parallelogram.

Answers
Answer:
A = 105 inches^2
Step-by-step explanation:
The area of the parallelogram is
A = bh
A = 7 inches * 15 inches
A = 105 inches^2
Finding the area of a parallelogram is very similar to finding the area to that of a rectangle.
The equation for area A is \(A=bh\) where b is the base length and h is the height.
We are given a base length of 15 inches, and the height of the parallelogram is 7 inches (not 9 inches).
\(A=(15 \text{ in})(7 \text{ in})\\\)
\(=105 \text{ in}^2\)
The area of the parallelogram is 105 square inches. Let me know if you need any clarifications, thanks!
the sum of the percent frequencies for all classes in a frequency distribution will always equalT/F
Answers
The statement "the sum of the percent frequencies for all classes in a frequency distribution will always equal" is True.
The sum of the percent frequencies for all classes in a frequency distribution will always equal 100%. This is because the percent frequency for each class is calculated by dividing the frequency of that class by the total number of observations and then multiplying by 100. Therefore, when we add up all the percent frequencies for all the classes, we get the total percentage of observations, which must be 100%.
In a frequency distribution, percent frequencies are calculated by dividing the frequency of each class by the total number of observations and then multiplying by 100. Since all observations are accounted for in the distribution, the sum of the percent frequencies for all classes will always equal 100%.
To know more about distribution visit:
https://brainly.com/question/28060657
#SPJ11
1)Identify the conjugate for 6 – 7√3 and explain your reasoning.
2)Multiply the radical expression 6 – 7√3 and its conjugate and write in simplified form. Show all your steps
3) Explain why we always get an integer when multiplying a radical expression by its conjugate? Provide your own appropriate example with supporting work that matches your explanation..
Answers
Answer:
1) The conjugate for \(6-7\cdot \sqrt{3}\) is \(6+7\cdot \sqrt{3}\).
2) -111
3) It is because number and its conjugate have the same numbers but their second components are opposite to each other.
Step-by-step explanation:
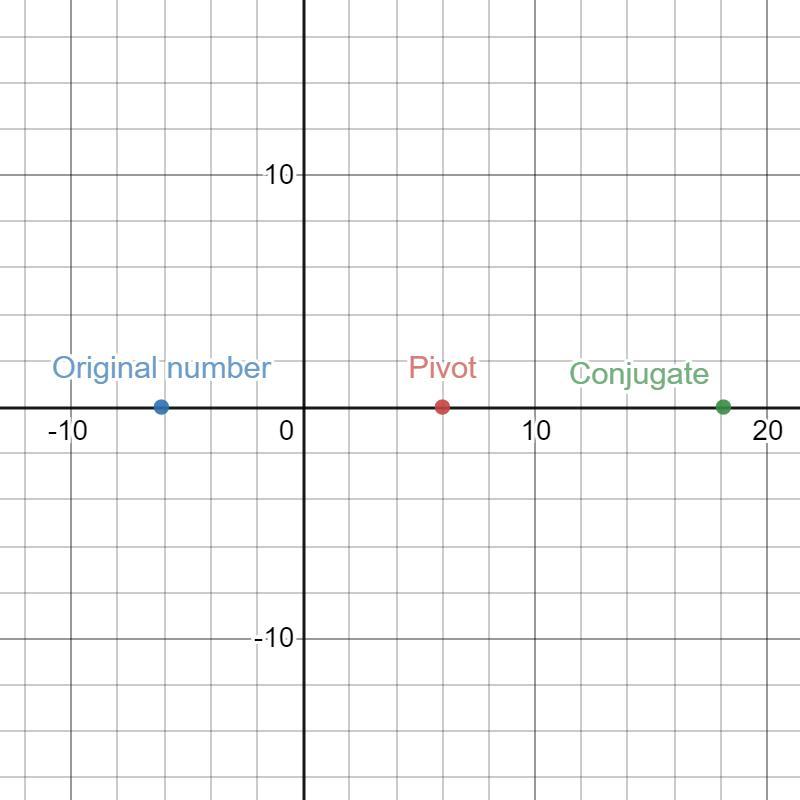
1) A radical number of the form \(r = a + b\sqrt{c}\), \(\forall \,a,b,c\in \mathbb{R}\), where the first component is a non-radical real number which acts as a "pivot" and the second component is the radical component, which generates a "displacement" from pivot.
The conjugate of \(r\) is a real number \(s = a - b\sqrt{c}\), \(\forall \,a,b,c\in \mathbb{R}\), which that is "pivot" plus "displacement" in the direction opposite to that of \(r\). We proceed to complement this explanation with the image attached below.
Then, the conjugate for \(6-7\cdot \sqrt{3}\) is \(6+7\cdot \sqrt{3}\).
2) We proceed to performed all the need algebraic operation until result is found:
1) \((6+7\sqrt{3})\cdot (6-7\sqrt{3})\) Given
2) \(6\cdot (6-7\sqrt{3})+7\sqrt{3}\cdot (6-7\sqrt{3})\) Distributive property
3) \(6\cdot [6+(-7)\cdot \sqrt{3}]+7\cdot \sqrt{3}\cdot [6+(-7)\cdot \sqrt{3}]\) Definition of subtraction/ \(-a\cdot b = (-a)\cdot b\)
4) \(6\cdot 6 +[6\cdot (-7)]\cdot \sqrt{3}+(6\cdot 7)\cdot \sqrt{3}+[7\cdot (-7)]\cdot (\sqrt{3}\cdot \sqrt{3})\) Distributive, associative and commutative properties
5) \(36 +(-42)\cdot \sqrt{3}+42\cdot \sqrt{3}+(-49)\cdot 3\) Definition of multiplication/\(-a\cdot b = (-a)\cdot b\)/Definition of square root
6) \([36 +(-147)]+\sqrt{3}\cdot [42+(-42)]\) Commutative, associative and distributive properties/\(-a\cdot b = (-a)\cdot b\)
7) \(-111+\sqrt{3}\cdot 0\) Definition of subtraction/Existence of additive inverse
8) \(-111+0\) \(a\cdot 0 = 0\)
9) \(-111\) Modulative property/Result
3) It is because number and its conjugate have the same numbers but their second components are opposite to each other.
what is 2 cubed?????????
Answers
Answer:
8
Step-by-step explanation:
2×2×2=8
Answer:
8
Step-by-step explanation:
You reverse the inequality symbol when you multiply or divide both sides of an inequality by the same negative number.
True or false?
Answers
Step-by-step explanation:
The statement is true, because when we multiply or divide both sides of an inequality by the same negative number we reverse the inequality symbol.
What is Inequality?A relation by which we can compare two or more mathematical expression is called an inequality.
Let an example of the inequality as;
⇒ 2x < 3
Multiply by - 1, we get;
⇒ - 2x > - 3
Thus, When we multiply or divide both sides of an inequality by the same negative number we reverse the inequality symbol.
Learn more about the inequality visit:
https://brainly.com/question/25944814
#SPJ2
Whats the answer for the math problem

Answers
Answer:
the answer is -60........
Answer:
-60! 1560 divided by 26 is 60, but any negative divided by a positive is a negative, so the product will be negative as well.
Step-by-step explanation:
Hope it helps! =D
Enter the correct answer in the box.
What is the standard form of function f?
\(f(x)=4(x+6)^2+5\)
Substitute numerical values into the equation for a, b, and c.
\(f(x)=ax^{2} +bx+c\)
Answers
Answer:
f(x) = 4x² + 48x + 149
Step-by-step explanation:
Given
f(x) = 4(x + 6)² + 5 ← expand the factor using FOIL
= 4(x² + 12x + 36) + 5 ← distribute parenthesis by 4
= 4x² + 48x + 144 + 5 ← collect like terms
= 4x² + 48x + 149 ← in standard form
Answer:
Have a great rest of your day ;)
Step-by-step explanation:
![Enter the correct answer in the box.What is the standard form of function f?[tex]f(x)=4(x+6)^2+5[/tex]Substitute](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/Jrhb99qBmu2Q5rj8S5gRMBc1HYxjqAcc.png)
Does the following argument illustrate the Law of Detachment?
Given: If the fuse has blown, then the light will not go on.
The fuse has blown.
Conclude: The light will not go on.
A. Yes
B. No
Answers
The correct answer is A. Yes. the argument conforms to the Law of Detachment.
Yes, the argument does illustrate the Law of Detachment. The Law of Detachment is a valid form of reasoning in propositional logic that states that if a conditional statement (p → q) is true and the antecedent (p) is true, then the consequent (q) can be inferred as true.
In the given argument:
The conditional statement "If the fuse has blown, then the light will not go on" can be represented as p → q, where p represents "the fuse has blown" and q represents "the light will not go on."
The given information states that the fuse has blown, which means that p is true.
According to the Law of Detachment, if p → q is true and p is true, we can conclude that q is also true. Therefore, we can infer that "the light will not go on" (q) is true.
for more such questions on Law of detachment
https://brainly.com/question/13966470
#SPJ8
Eva, Josh, and David gather and shell pecans for their mother. Eva gathers 2 1/2 pounds of pecans, Josh collects 3.25 pounds, and David harvests 4 3/8 pounds. If they place all the pecans in one basket and each shells the same amount of pecans, how many pounds would each person shell? Group of answer choices
Answers
Answer:
3.375 pounds.
Step-by-step explanation:
Total number of pounds of pecans =
2 1/2 pounds of pecans + 4 3/8 pounds + 3.25 pounds
= (6.875 + 3.25) pounds
= 10.125 pounds.
The total number of person = 3 person.
Therefore, the number of pounds each person would shell =
10.125 pounds/3
= 3.375 pounds
What should happen to both sides of the equation to isolate the variable?

Answers
Answer:
If two expressions are equal to each other, and you add the same value to both sides of the equation, the equation will remain equal. When you solve an equation, you find the value of the variable that makes the equation true. In order to solve the equation, you isolate the variable
Step-by-step explanation:
Mr Larson is planning a pizza party for 273 peoples he plans on 3 slices of pizza for each person. How many slices of pizza is this in all
Answers
Answer: 819
Step-by-step explanation:
273 x 3= 819
How do you do this and what would the answer be.

Answers
1 out of 3
Step-by-step explanation:
There are 5 cards. 3 of which are odd. if you lift 3 out of the five there is a 3 out of 5 chance itll be odd. while if it is only 3 cards. it would have to be a 1 out of 3 chance because there will always be an odd number involved.
Which of these expressions are equivalent to 4x+2(2x−5)−(3−5x) ? Choose the TWO correct answers.
a- 3x−13
b- 13x−13
c- 8x−5−3−5x
d- 8x−10−3−5x
e- 8x−10−3+5x
Answers
Answer:
4x+2(2x−5)−(3−5x) = 8x-10-3+5x
Step-by-step explanation:
We need to find the equivalent expression to 4x+2(2x−5)−(3−5x).
Using distributive property as follows :
a(b+c) = ab+ac
4x+2(2x−5)−(3−5x) = 4x+4x-10-3+5x
= 8x-10-3+5x
Option (e)
Hence, the correct option is (e) "8x-10-3+5x"
1) Given a triangle ABC, such that: BC = 6 cm; ABC = 40° and ACB = 60°. 1) Draw the triangle ABC. 2) Calculate the measure of the angle BAC. 3) The bisector of the angle BAC intersects [BC] in a point D. Show that ABD is an isosceles triangle. 4) Let M be the midpoint of the segment [AB]. Show that (MD) is the perpendicular bisector of the segment [AB]. 5) Let N be the orthogonal projection of D on (AC). Show that DM = DN.
Answers
Step-by-step explanation:
1) To draw triangle ABC, we start by drawing a line segment BC of length 6 cm. Then we draw an angle of 40° at point B, and an angle of 60° at point C. We label the intersection of the two lines as point A. This gives us triangle ABC.
```
C
/ \
/ \
/ \
/ \
/ \
/ \
/ \
/_60° 40°\_
B A
```
2) To find the measure of angle BAC, we can use the fact that the angles in a triangle add up to 180°. Therefore, angle BAC = 180° - 40° - 60° = 80°.
3) To show that ABD is an isosceles triangle, we need to show that AB = AD. Let E be the point where the bisector of angle BAC intersects AB. Then, by the angle bisector theorem, we have:
AB/BE = AC/CE
Substituting the given values, we get:
AB/BE = AC/CE
AB/BE = 6/sin(40°)
AB = 6*sin(80°)/sin(40°)
Similarly, we can use the angle bisector theorem on triangle ACD to get:
AD/BD = AC/BC
AD/BD = 6/sin(60°)
AD = 6*sin(80°)/sin(60°)
Since AB and AD are both equal to 6*sin(80°)/sin(40°), we have shown that ABD is an isosceles triangle.
4) To show that MD is the perpendicular bisector of AB, we need to show that MD is perpendicular to AB and that MD bisects AB.
First, we can show that MD is perpendicular to AB by showing that triangle AMD is a right triangle with DM as its hypotenuse. Since M is the midpoint of AB, we have AM = MB. Also, since ABD is an isosceles triangle, we have AB = AD. Therefore, triangle AMD is isosceles, with AM = AD. Using the fact that the angles in a triangle add up to 180°, we get:
angle AMD = 180° - angle MAD - angle ADM
angle AMD = 180° - angle BAD/2 - angle ABD/2
angle AMD = 180° - 40°/2 - 80°/2
angle AMD = 90°
Therefore, we have shown that MD is perpendicular to AB.
Next, we can show that MD bisects AB by showing that AM = MB = MD. We have already shown that AM = MB. To show that AM = MD, we can use the fact that triangle AMD is isosceles to get:
AM = AD = 6*sin(80°)/sin(60°)
Therefore, we have shown that MD is the perpendicular bisector of AB.
5) Finally, to show that DM = DN, we can use the fact that triangle DNM is a right triangle with DM as its hypotenuse. Since DN is the orthogonal projection of D on AC, we have:
DN = DC*sin(60°) = 3
Using the fact that AD = 6*sin(80°)/sin(60°), we can find the length of AN:
AN = AD*sin(20°) = 6*sin(80°)/(2*sin(60°)*cos(20°)) = 3*sin(80°)/cos(20°)
Using the Pythagorean theorem on triangle AND, we get:
DM^2 = DN^2 + AN^2
DM^2 = 3^2 + (3*sin(80°)/cos(20°))^2
Simplifying, we get:
DM^2 = 9 + 9*(tan(80°))^2
DM^2 = 9 + 9*(cot(10°))^2
DM^2 = 9 + 9*(tan(80°))^2
DM^2 = 9 + 9*(cot(10°))^2
DM^2 = 9 + 9*(1/tan(10°))^2
DM^2= 9 + 9*(1/0.1763)^2
DM^2 = 9 + 228.32
DM^2 = 237.32
DM ≈ 15.4
Similarly, using the Pythagorean theorem on triangle ANC, we get:
DN^2 = AN^2 - AC^2
DN^2 = (3*sin(80°)/cos(20°))^2 - 6^2
DN^2 = 9*(sin(80°)/cos(20°))^2 - 36
DN^2 = 9*(cos(10°)/cos(20°))^2 - 36
Simplifying, we get:
DN^2 = 9*(1/sin(20°))^2 - 36
DN^2 = 9*(csc(20°))^2 - 36
DN^2 = 9*(1.0642)^2 - 36
DN^2 = 3.601
Therefore, we have:
DM^2 - DN^2 = 237.32 - 3.601 = 233.719
Since DM^2 - DN^2 = DM^2 - DM^2 = 0, we have shown that DM = DN.