x+\(\sqrt{x}\)+1 / \(\sqrt[3]{x}\)
Answers
Related Questions
Plz help asap you might get the brilliant

Answers
Answer:
In step 2
Step-by-step explanation:
In order to balance both sides, you first have to add 3c to both sides, but instead, it is subtracted in step 2, skewing the entire rest of the problem.
Answer:
Instead of subtracting 6, you should add 6 to both sides.
Step-by-step explanation:
nice levi pfp btw :)

The linear correlation coefficient for a set of paired variables is r=0.897. what proportion of the variation in y acn be explained by the linear relationship between x and y?
Answers
About \(80.5\%\) of the variation in y can be attributed to the linear relationship with x.
Used the concept of correlation coefficient that states,
The proportion of the variation in y that can be explained by the linear relationship between x and y can be determined by squaring the correlation coefficient
Given that,
When paired variables are considered, the linear correlation coefficient is,
\(r=0.897\)
Hence the proportion of the variation in y explained by x is,
\(r^2 = (0.897)^2\)
\(r^2 = 0.804609\)
This means that about \(80.5\%\) of the variation in y can be attributed to the linear relationship with x.
Learn more about the correlation coefficient here:
brainly.com/question/27226153.
#SPJ12
Alice and Bob both go to a party which starts at $5:00$. Each of them arrives at a random time between $5:00$ and $6:00$. What is the probability that the number of minutes Alice is late for the party plus the number of minutes Bob is late for the party is less than $45$
Answers
The probability comes out to be 9/32.
Deducing Arrival Time Possibility
All the possible arrival times by Alice and Bob, in minutes after 5 PM, is constrained by the values of given values of x and y,
x = 0, y = 0, x = 60, y = 60.
Here, let the values of x represent how many minutes after 5 PM Alice arrives at the party.
Let the y values represent the time in minutes that Bob arrives at the party after 5 PM.
Calculating the Required Probability
The times that concern us, however, are obtained by the following probability function,
x + y ≤ 45.
And x = 0, y = 0, and x + y ≤ 45 define the constraints of this probability function. Thus the perimeter of such a graph will be given as,
(45² / 2) = 1012.5 square units
Since the total area of the various arrival times is 60 x 60, or 3600 square units, the probability that Alice and Bob will arrive together after 5 o'clock in the evening in less than 45 minutes is therefore = 1012.5 / 3600 = 9/32
Learn more about probability here:
https://brainly.com/question/11234923
#SPJ4
A ladder company produces blue ladders and green ladders. There is a demand of at least 100 blue ladders and 70 green ladders per day. Due to costs, no more than 160 blue ladders and no more than 150 green ladders can be produced per day. To satisfy a contract with a store, a total of at least 215 ladders must be shipped each day. If each blue ladder sold results in a $5 profit and each green ladder sold results in a $3 loss, how many green ladders should be produced to net a profit of $155? Please provide the numerical solution without any units
Answers
To determine the number of green ladders that should be produced to net a profit of $155, we need to consider the given constraints and objectives.
The company must ship at least 215 ladders per day to satisfy the contract with the store. Let's denote the number of blue ladders produced per day as "B" and the number of green ladders produced per day as "G". Based on the demand requirements, we have the following inequalities:
B ≥ 100 (demand for blue ladders)
G ≥ 70 (demand for green ladders)
To satisfy the cost limitations, we have:
B ≤ 160 (maximum blue ladders production)
G ≤ 150 (maximum green ladders production)
The total number of ladders produced per day is B + G, and we want this to be at least 215. Now, let's consider the profit calculation. Each blue ladder results in a $5 profit, while each green ladder results in a $3 loss. The total profit can be calculated as 5B - 3G.
To net a profit of $155, we set up the equation:
5B - 3G = 155
We need to find the value of G that satisfies all the constraints and gives us the desired profit. This involves solving the system of inequalities and the equation simultaneously. Unfortunately, without specific values for the production quantities or additional constraints, it is not possible to provide a numerical solution. The solution would require applying linear programming techniques to find the feasible region and optimize the profit.
Learn more about inequalities here: brainly.com/question/28823603
#SPJ11
Solve x = 5x + 6.
Do not include extraneous solutions.
x =
[?]
![Solve x = 5x + 6.Do not include extraneous solutions.x =[?]](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/ExVHvC1GbfQmLJMWMTbE9u6ZF83hhM2v.png)
Answers
Answer:
6
Step-by-step explanation:
Answer:
It might be 11 but u try ur best
Find the measure of the arc.
B
C
1469 E
A
mFD = [?]°
Enter
4
![Find the measure of the arc.BC1469 EAmFD = [?]Enter4](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/AOXEUwKch343zRLzjooFYKdYb5UDmHVM.png)
Answers
The measure of arc FD = 236 degree.
In the given figure
The measure of arc FE = 146
And Measure of arc ED is right angle.
We know that right angle = 90 degree
Then,
And Measure of arc ED is right angle.
Since we know,
An "arc" is a smooth curve that connects two locations.
In general, an arc is a section of a circle.
It is essentially a portion of a circle's circumference.
An arc is a kind of curve. An arc can be a section of another curved form, such as an ellipse, although it most commonly refers to a circle.
From figure,
The arc FD consist of FE and ED
Therefore,
To find the measure of arc FD add the measure of arc FE and ED
So,
mFD = 146 + 90
= 136
Hence,
⇒ mFD = 236 degree.
To learn more about cirlce visit:
https://brainly.com/question/29288238
#SPJ1
Aliyah had some candy to give to her four children. She first took ten pieces for herself and then evenly divided the rest among her children. Each child received two pieces. With how many pieces did she start with?
Answers
Answer: 18 pieces
Step-by-step explanation:
If she took 10 pieces and then each child received 2 pieces and she has four children then
10+2+2+2+2=
10+8=
18
find the value of x.
x=
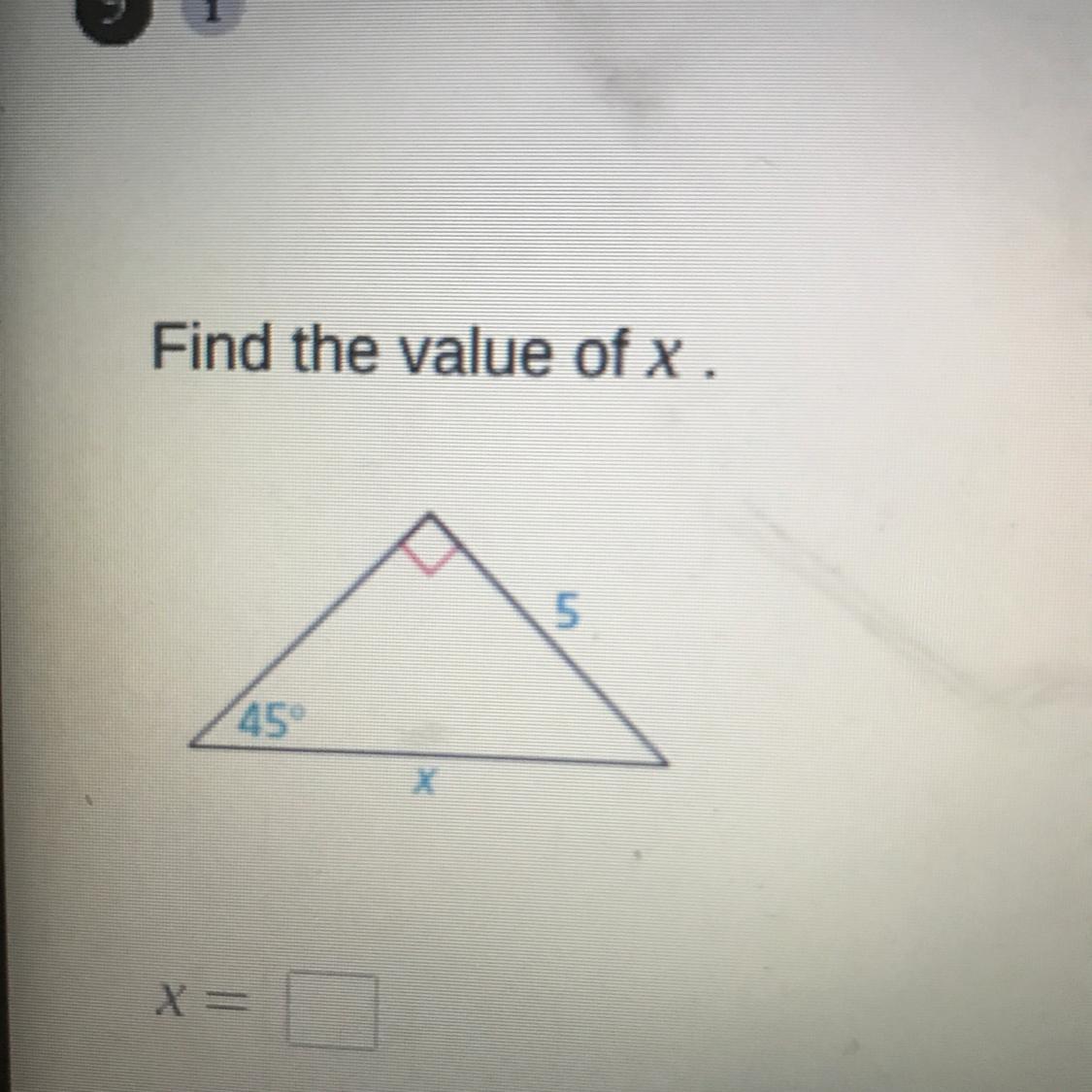
Answers
Answer:
the value of x is a whopping 90 degrees
x = 5√2
Step-by-step explanation:
Hypotenuse (h) = x
perpendicular (p) = 5
Now
Sin 45° = p/h
1/√2 = 5 / x
Cross multiply
x = 5√2
Hope it will help
A characteristic of a simple random sample is that all samples of the same _______ have an equal chance to be selected.
Answers
A characteristic of a simple random sample is that all samples of the same population have an equal chance to be selected.
What is a simple random sampling?A subset of a statistical population called a simple random sample is one in which each member has the same chance of being picked or selected.
A subset of participants is chosen at random by the researcher using this sampling approach from a population.
To make sure that the sample represents the population, simple random sampling is often performed and this technique helps to sample bigger populations more frequently than smaller subpopulations.
Learn more about simple random sampling here:
https://brainly.com/question/3139978
#SPJ1
A sample of a radioactive isotope had an initial mass of 110 mg in the year 1990 and decays exponentially over time. A measurement in the year 1993 found that the sample's mass had decayed to 90 mg. What would be the expected mass of the sample in the year 2002, to the nearest whole number?
Answers
50 mg be the expected mass of the sample in the year 2002, to the nearest whole number
In 1990, a sample of a radioactive isotope had an initial mass of 110 mg and decayed exponentially over time.
A measurement in 1993 revealed that the sample's mass had decayed to 90
110 mg - 90 mg = 20 mg (amount decayed in the 3 total years)
20 mg ÷ 3 years = 6.6 mg decayed per year
6.6 × 9 years (years between 1993 and 2002) = 60 mg
110 mg - 60 mg = 50 mg, rounded to 50 mg
50 mg be the expected mass of the sample in the year 2002, to the nearest whole number
To learn more about whole number:
https://brainly.com/question/19161857
#SPJ4
Can someone please help me with all of these? i really need help!

Answers
The solution to the following equations are:
x + 8 = 6; x = -2x - 1 = -4; x = -310 + x = 5; x = -5x + 4 = -14; x = -18x - 3 = -9; x = -6-4 + x = -8; x = -4-5 = 10x; x = -0.5-4x = -60; x = 153x = -24; x = -8What are the solution to the equations?x + 8 = 6
subtract 8 from both sides
x = 6 - 8
x = -2
x - 1 = -4
Add 1 to both sides
x = -4 + 1
x = -3
10 + x = 5
subtract 10 from both sides
x = 5 - 10
x = -5
x + 4 = -14
subtract 4 from both sides
x = -14 - 4
x = -18
x - 3 = -9
Add 3 to both sides
x = -9 + 3
x = -6
-4 + x = -8
Add 4 to both sides
x = -8 + 4
x = -4
-5 = 10x
divide both sides by 10
x = -5/10
x = -0.5
-4x = -60
divide both sides by -4
x = -60/-4
x = 15
3x = -24
divide both sides by 3
x = -24/3
x = -8
Read more on algebra:
https://brainly.com/question/4344214
#SPJ1
It is given that A⃗ −B⃗ =(−51.4m)x^,C⃗ =(62.2m)x^, and A⃗ +B⃗ +C⃗ =(13.8m)x^.
Find the vector A⃗ . Find the vector B⃗ .
Answers
The vector A is (49.9m) x and vector B is (1.5m) x.
In the given question, A − B = (−51.4m)x, C =(62.2m)x, and A +B +C =(13.8m)x.
Find the vector A. Find the vector B.
We may disregard the vector x and treat the issue as an arithmetic one since all of the measurements are in the same direction (simultaneous equations).
A − B = −51.4.............................(1)
C = 62.2.............................(2)
A + B + C = 13.8.............................(3)
Now putting the value of C from Equation (2) in Equation (3)
A + B + C = 13.8
A + B + 62.2 = 13.8
Subtract 62.2 on both side, we get
A + B = 13.8 - 62.2
A + B = - 48.4.....................(4)
Adding the equation (1) and (4), we get
2A = - 99.8
Divide by 2 on both side, we get
A = - 49.9
Now subtracting the equation (1) and (4), we get
2B = -48.4 - ( -51.4)
2B = 3
Divide by 2 on both side, we get
B = 1.5
Since all of the calculations are done in terms of the unit vector x.
So the answer is vector B = (1.5m) x and vector A = (49.9m) x.
To learn more about vector link is here
brainly.com/question/29740341
#SPJ4
HELLLP khan academy !! due tonight

Answers
Equation of the line is y = -(1/3)x+5
The figure shows a straight line of which two points and thereby the slope can be found out.
Equation of a line is in the slope-intercept form is,
y = mx +c,
where m is the slope of the line and c is the y-intercept of the line.
From the figure, two points on the line are, (0,5) and (3,4).
Then slope = (4-5)/(3-0)
= -1/3
Now y-intercept, c is the y-co-ordinate when x = 0.
From the figure, when x = 0, y = 5
So y-intercept, c = 5.
Thus the equation of the line is, y = -(1/3)x+5
Learn more about slope-intercept form at https://brainly.com/question/16975427
#SPJ1
Can someone please help me to solve 5/6 only I will mark you the brainly pls I need help please please

Answers
Answer:
5. h = 12
6. k = 17, m = 12
Step-by-step explanation:
5. The sum of angles on the adjacent side of a diagonal of a parallelogram is 180 degree
\(3h + 24 = 4 h + 12\\h = 12\)
6. The angle is 90 degrees
\(5k + 5 = 90\\k = 17\\7m + 6 = 90\\m = 12\)
Find the area of hexagon DEFGHI.

Answers
Step-by-step explanation:
Break it up into two trapezoids as shown
area = trap1 + trap2
= 2 * (7+3) / 2 + 3 * ( 7 + 3) / 2 = 10 + 15 = 25 units^2

John earns a 3% commission for every car he sells. Today he sold a car for $13,600. How much commission did he receive? (To find commission you just change your percent to a decimal and multiply it times the sales.)
Answers
Answer:
$408
Step-by-step explanation:
What we know:
John earns a 3% commission for every car he sells.
He sold a car today for $13,600.
Multiply 3/100 by 13,600 to get your answer.
3/100 * 13600
40800/100
$408 in commission
Answer:
3/100x13600
commission = $408
2x + 16 = 22x
Variables on both sides
Answers
answer: Subtract sixteen from both sides of the equation
2 +16 -16=22x -16
x = 4/5
The 99% confidence interval for a population mean is (9, 15). At the 5% significance level, which of the following null hypotheses can be rejected?
(a) The population mean is less than or equal 15
(b) The population mean is greater than or equal to 9
(c) The population mean is greater than or equal to 15
(d) The population mean is 12
Answers
Based on the given confidence interval, the null hypotheses (c) and (d) can be rejected at the 5% significance level.
To determine which null hypothesis can be rejected at the 5% significance level, we need to compare it with the confidence interval.
The 99% confidence interval (9, 15) means that we are 99% confident that the true population mean falls between 9 and 15.
At the 5% significance level, we reject a null hypothesis when the hypothesized value falls outside the confidence interval.
Let's analyze each option:
(a) The population mean is less than or equal to 15.
Since the upper bound of the confidence interval is 15, this null hypothesis cannot be rejected.
(b) The population mean is greater than or equal to 9.
Since the lower bound of the confidence interval is 9, this null hypothesis cannot be rejected.
(c) The population mean is greater than or equal to 15.
Since the lower bound of the confidence interval is 9, which is less than 15, this null hypothesis can be rejected.
(d) The population mean is 12.
Since the null hypothesis specifies a specific value (12), and the confidence interval (9, 15) does not include 12, this null hypothesis can be rejected.
Based on the given confidence interval, the null hypotheses (c) and (d) can be rejected at the 5% significance level.
To know more about equation click-
http://brainly.com/question/2972832
#SPJ11
Find the value(s) of k such that the function is continuous at x=-1. (Enter your answers as a comma-separated list. If an answer does not exist, enter DNE.)
{In(2x+5) x < -1
F(x) = {8x - k x ≥ -1
Answers
To find the value(s) of k such that the function is continuous at x = -1, we need to equate the two pieces of the function at x = -1 and ensure that the limit of the function approaches the same value from both sides.
Let's evaluate the function at x = -1:
For x < -1, the function is f(x) = ln(2x + 5), so at x = -1, we have f(-1) = ln(2(-1) + 5) = ln(3).
For x ≥ -1, the function is f(x) = 8x - k, so at x = -1, we have f(-1) = 8(-1) - k = -8 - k.
For the function to be continuous at x = -1, the values of ln(3) and -8 - k should be equal. Therefore, we can set up the equation:
ln(3) = -8 - k.
Solving this equation for k, we have:
k = -8 - ln(3).
Hence, the value of k that makes the function continuous at x = -1 is k = -8 - ln(3).
In summary, the value of k that ensures the function is continuous at x = -1 is k = -8 - ln(3).
Learn more about equation here:
brainly.com/question/29657983
#SPJ11
Find the perimeter of the figure. PLEASE HELP ASAP I’LL MARK BRAINLIEST

Answers
Answer:
I believe it should be 32
Step-by-step explanation:
Answer:
32
Step-by-step explanation:
hope this helps!
help help help help please

Answers
4Th option is correct ✔️ ✔️
Answer:
Maybe Option D but I'm not sure
a recipe for bread uses 2 cups of liquid and 6 cups of flour for 3 loaves of bread. how many cups of flour are needed for 10 loaves and how much liquid is needed if 21 cups of flour are used?
Answers
10
Step-by-step explanation:
I just did this in a lesson
plzzzzzzzzzzzzzz help fast

Answers
Answer:
c is the answers for the question
Step-by-step explanation:
please give me brainlest
Answer:
x =(-2-√-116)/-10=(1+i√ 29 )/5= 0.2000-1.0770i
x =(-2+√-116)/-10=(1-i√ 29 )/5= 0.2000+1.0770i
Step-by-step explanation:
\(\sqrt{49x^{2}\)
Answers
The square root of 7x is = \(\mathrm{\sqrt{49x^2} }\) so 49 can be divided by 7, comparable sides that create a right angle in a parallelogram.
What is square?Per the Geometric forms, a square is an isosceles quadrilateral having four equal corners and four equal angles. It is sometimes refereed to as a parallelogram with two adjacent faces of the same length. A triangle is a symmetrical quadrilateral because it has 3 equal sides and four equal angles.
Square angles are those that have 90 degrees or straight. The diagonals of the square are also placed horizontally and divided at a right angle. a nearby rectangle with two sides of identical length. a hexagon with four equal-length sides and fourth right angles. two neighboring, comparable sides that create a right angle in a parallelogram. an equilateral fractal pattern.
Given
= \(\mathrm{\sqrt{49x^2} }\)
= \(\mathrm{\sqrt{7 \times 7\times x \times x} }\)
= 7x
The square root of 7x is = so 49 can be divided by 7, comparable sides that create a right angle in a parallelogram.
To know more about square visit:
brainly.com/question/14198272
#SPJ1
Complete question:
Factor the given expression to simplest form to the simplest form
\(\mathrm{\sqrt{49x^2} }\)
A tv show had 3.6 x 104 viewers in the first week and 4.1 x 104 viewers in the second week. determine the average number of viewers over the two weeks and write the final answer in scientific notation. 3.85 x 104 7.7 x 104 3.85 x 108 7.7 x 108
Answers
The average number of viewers over the two weeks written in scientific notation is 3.85 × 10^8. option C
Scientific notationFirst week = 3.6 x 10⁴Second week = 4.1 x 10⁴Average number of viewers over the two weeks = (First week + Second week) / 2
= {(3.6 x 10⁴) + (4.1 x 10⁴)} / 2
= {3.6 + 4.1 × 10^(4×4) } / 2
= (7.7 × 10^16) / 2
= 3.85 × 10^8
Therefore, the average number of viewers over the two weeks written in scientific notation is 3.85 × 10^8.
Learn more about scientific notation:
https://brainly.com/question/27862246
#SPJ4
Find the slope of the line through each pair of points. (-1/2 ,-1/2) and (-3,-4)
Answers
The slope of the line with points (-1/2 ,-1/2) and (-3,-4) is 1.4
What is a slope of line?A line's steepness and direction are determined by the slope of the line. Without actually using a compass, determining a line's slope in a coordinate plane allows one to anticipate whether a line is parallel, perpendicular, or not.
The change in a line's y coordinate relative to its change in x coordinate is referred to as the line's slope. Δy is the net change in the y coordinate, while Δx is the net change in the x coordinate.
Therefore,
m = y₂-y₁/x₂-x₁ (where m denotes the slope) can be used to express how the y coordinate changes in relation to the x coordinate.
Be aware that tan ∅ = y/x
We also refer to this tan as the line's slope
We know that slope, slope = m = \(\frac{y_2 - y_1}{x_2 - x_1}\)
For the pairs of points (-1/2 ,-1/2) and (-3,-4)
⇒ m = \(\frac{-4- (-1/2)}{-3 - (-1/2)}\)
⇒ m = \(\frac{-7/2}{-5/2 }\)
⇒ m = 7/5
⇒ m = 1.4
Hence, the slope of the line with points (-1/2 ,-1/2) and (-3,-4) is 1.4
Learn more about slope
brainly.com/question/16949303
#SPJ4
Simplify.
5 • 2 • (–4) + 6 ÷ 2
Answers
Answer:
- 37
Step-by-step explanation:
5 • 2 • ( - 4 ) + 6 ÷ 2
= 5 • 2 • ( - 4 ) + [ 6 ÷ 2 ]
= 10 • ( - 4 ) + 3
= - 40 + 3
= - 37
the purpose of sampling is to select a set of elements from a population so that the descriptions of the sample accurately portray the population. this is best achieved through the use of
Answers
The purpose of random sampling is to select a set of items from a population such that the sample description accurately represents the population.
Random sampling is a type of sampling in which the researcher randomly selects a subset of participants from a population. Each member of the population has an equal chance of being selected. Data is then collected from as high a percentage of this random subset as possible. Simple random sampling selects a smaller group (sample) from a larger group of the total number of participants (population).
Samples are at the heart of survey research. It is often called the population microcosm, and the process of drawing a sample should maximize the similarity of the sample to the population under study. Sampling is therefore the selection of a set of elements from a population whose description accurately describes the parameters of the total population from which the sample is selected.
For more information about random sampling, visit :
https://brainly.com/question/30403914
#SPJ4
Select the correct answer from each drop down menu. In the figure, AB=__inches and AC=___
10" inches

Answers
Answer: In the figure AB is about 8.4 inches and AC is about 13.05 inches.
Step-by-step explanation: We can use cosine to find the hypotenuse. \(cos(40)=\frac{10}{x} \\cos(40) (x)=\frac{10}{x}(x)\\cos(40) (x) =10\\\frac{cos(40) (x)}{cos (40)} =\frac{10}{cos (40)} \\x=\frac{10}{cos(40)}\)
Using a calculator x is about 13.05
Using tangent we can find the length opposite of <C
\(tan(40)=\frac{x}{10} \\tan(40) (10)=\frac{x}{10}(10)\\tan(40) (10) = x\)
Using a calculator x would be about 8.4
Answer:
Step-by-step explanation:

two cars start moving from the same point. one travels south at 64 mi/h and the other travels west at 48 mi/h. at what rate is the distance between the cars increasing four hours later?
Answers
One car travel South at 64 mi/h and the other travels west at 48 mi/h. The distance between the cars increases with rate at 80 mi/h.
To find the rate of change, we need to find the derivative of the variables with respect to time.
Let:
p = distance between 2 cars
q = distance between car 1 and the start point
r = distance between car 2 and the start point
Using the Pythagorean Theorem:
p² = q² + r²
Take the derivative with respect to time:
2p dp/dt = 2q dq/dt + 2r dr/dt
dq/dt = speed of car 1 = 64 mi/h
dr/dt = speed of car 2 = 48 mi/h
The distance of car 1 and car 2 from the start point after 4 hours:
q = 64 x 4 = 256 miles
r = 48 x 4 = 192 miles
Using the Pythagorean theorem:
p² =256² + 192²
p = 320 miles
Hence,
2p dp/dt = 2q dq/dt + 2r dr/dt
p dp/dt = q dq/dt + r dr/dt
320 x dp/dt = 256 x 64 + 192 x 48
dp/dt = 80
Hence, the distance between the cars increases with rate at 80 mi/h
Learn more about rate of change here:
https://brainly.com/question/24873957
#SPJ4