Write the following polynomial in standard form:
\(7x^{3} + 5x^{2} - 2x^{6} +3x^{2} -4\)
Answers
-2x^6+7x^3+8x^2-4 :)
Related Questions
- (9m + 12) = 6(14 - m) ?
Answers
Answer:
m=-32
Step-by-step explanation:
Answer:
M=(-32)
Step-by-step explanation:
-(9m+12)=6(14-m)
-(9m+12)=84-6m
-9m-12=84-6m
-9m+6m-12=84
-3m-12=84
-3m-12+12=84+12
-3m=96
-3m÷(-3)=96÷(-3)
m=(-32)
This square-based oblique pyramid has a volume of 125\text{ m}^3125 m 3 125, start text, space, m, end text, cubed. What is the height of the pyramid
Answers
To find the height of the pyramid, we need to use the formula for the volume of a square-based oblique pyramid, which is given by:
\(Volume = (1/3) * Base Area * Height\)
Given that the volume of the pyramid is 125 m^3 and the base area is unknown, we can rearrange the formula to solve for the height:
\(Height = Volume / ( (1/3) * Base Area )\)
Since the base of the pyramid is square-based, the base area can be found by taking the square of one of the sides. Let's call this side length "s". The base area is s^2.
Now, substitute the given values into the equation:
\(125 = (1/3) * s^2 * Height\)
To find the height, we need to isolate it on one side of the equation. Multiply both sides by 3:
\(375 = s^2 * Height\)
Next, divide both sides by \(s^2\):
\(Height = 375 / s^2\)
Since we don't know the value of s, we cannot determine the exact height of the pyramid. Without additional information, we can only express the height of the pyramid in terms of the side length "s" as\(Height = 375 / s^2.\)
To know more about pyramid visit:
https://brainly.com/question/13057463
#SPJ11
The height of the pyramid can be determined by evaluating the expression (3 * 125) / (√B).
The volume of a square-based oblique pyramid is given by the formula V = (1/3) * B * h, where V represents the volume, B represents the area of the base, and h represents the height of the pyramid.
In this case, the volume of the pyramid is given as 125 m³. We need to find the height of the pyramid.
We know that the base of the pyramid is a square, so the area of the base can be calculated using the formula A = s², where s represents the length of one side of the square base.
To find the height, we can rearrange the formula for the volume: h = (3V) / (B).
First, let's find the area of the base. Since the base is square-based, the area of the square can be found by taking the square root of the base area.
Let's assume the side length of the square base is s meters. Thus, the area of the base is A = s² = √B.
Now, substitute the values into the formula to find the height: h = (3 * 125) / (√B).
This is how to find the height of the given square-based oblique pyramid with a volume of 125 m³.
Learn more about volume
https://brainly.com/question/28058531
#SPJ11
What does it mean to factor a polynomial?
Answers
Answer:
Factoring a polynomial is the process of decomposing a polynomial into a product of two or more polynomials.
Hope this helps!!
please help meeee
from edge about graphing an absolute value function
determine the domain and range of the function f(x)= -|x| + 2.
the domain of the function is__________
the range of the function is__________
the options are: all real numbers, all numbers greater than or equal to 2, and all numbers less than or equal to 2
Answers
Answer:
For the given function f(x)= -|x| + 2
the domain of the function is: All real numbers
the range of the function is: all numbers greater than or equal to 2
Step-by-step explanation:
We need to find the domain and range of the function f(x)= -|x| + 2.
Domain: Domain is defined as all the possible x values of x for which the function is true.
Range: Range is defined as all the possible y values.
So, For the given function f(x)= -|x| + 2
the domain of the function is: All real numbers (the function is true for all real numbers)
the range of the function is: all numbers greater than or equal to 2
(When solving the equation we will have value of f(x) equal or greater than 2)
The hypotenuse of the right triangle is 5y inches long. The lengths of the legs are x + 8 and x + 3 inches. If the perimeter of the triangle is 60 inches and the length of the hypotenuse minus the length of the shorter leg is 10 inches, how many inches long is the hypotenuse?
Answers
Answer:
25
Step-by-step explanation:
The perimeter of triangle is equal to the sum of all sides of triangle
then:
5y + (x+8) + (x+3) = 60
5y + 2x +11 = 60
5y +2x = 49 ..............................................................(1)
the hypotenuse - shorter leg = 10
hint ( shorter leg ) = x+3
then
5y - (x + 3 ) = 10
5y - x - 3 = 10
5y - x = 13 .................................................... (2)
from 1 and 2
5y +2x = 49 .................................................................. (3)
5y - x = 13 (multiply both sides by 2 )
10y - 2x = 26 ..................................................................(4)
by sum 3 and 4
15y = 75
then y = 75/15 = 5
then hypotenuse = 5y = 5 x 5 = 25
Answer:
5
Step-by-step explanation:
Please help me solve this problem

Answers
Answer:
you do this in your own
Step-by-step explanation:
solve this problem
pls help me how do I round 9.4725 to the nearest cent with no dollar sign
Answers
Rounding off 9.4725 to the nearest cent will give 9.5
Rounding Off NumbersRounding off means a number is made simpler by keeping its value intact but closer to the next number. It is done for whole numbers, and for decimals at various places of hundreds, tens, tenths. When rounding money to the nearest cent, look at the number to the right of the full cents. In this case, that number is 9. If the number is five or more, increase the cents by 1. If the number is four or less, keep the cents the same. Because 9 is more than 5, $3.299 rounds to $3.30.
Applying same principle or concept here, we can round off 9.4725 to the nearest cent to give 9.5.
Learn more on rounding off numbers here;
https://brainly.com/question/25870256
#SPJ1
Could someone help me?

Answers
Hope that helps
why we shouldn't tease our friends in school
Answers
Answer:
no you should. i literally bully my friends
Step-by-step explanation:
Answer:
Because its mean
Step-by-step explanation:
Discuss the steps that you used to create your tangent line in #1. What was the most important step? Your discussion should be a minimum of three sentences
Answers
To create a tangent line, 1st we need to know the points at which the tangent is to be located, then calculate the slope and finally with the help of these points and slope we can construct the equation of tangent line.
We need to take the following steps in order to build a tangent line:
We start by locating the curve point to which we want to locate the tangent line. Say, these points are \(x_1\) and \(y_1\)The slope (m) of the curve at that point is then determined by taking the function's derivative. The slope displays the function's rate of change at that precise location. The equation of the tangent line is then created by entering the coordinates of the point and the slope using the line's point-slope form. This equation is as follows: \(y - y_1 = m (x - x_1)\)Hence, the above three steps are crucial to create a tangent line.
Learn more about tangent line here:
https://brainly.com/question/34259771
#SPJ12
Cookies are sold in the lunchroom for $1.50. Ana wants to buy cookies for a
group of her friends. If she has $20, which inequality can be solved to show the
Answers
Pls answer my question
X+3=?
Answers
help me pleaseeeeeeee

Answers
Answer:
Those are the answers. hope it helps

If S is a nonempty set, P(S) is defined to be the product of the elements in S. What is the sum of the values of P(S) over all the nonempty subsets S of {1/3, 1/4, 1/5, 1/6, 1/7, 1/8, 1/9, 1/10}? Express your answer as a common fraction.
Answers
When the problem is solved using fraction addition, the answer is 3601/2520 in common fraction.
What do we mean when we say that we add fractions?The three simple stages for adding fractions are as followsStep 1: Confirm that the denominators, or bottom numbers, are the same.Step 2: Add the top numbers, or the numerators, and position the result above the denominator.Step 3: Simplify the fraction as necessary.Subset S has the following values: 1/3, 1/4, 1/5, 1/6, 1/7, 1/8, 1/9, and 1/10.
1/3 + 1/4 + 1/5 + 1/6 + 1/7 + 1/8 + 1/9 + 1/103601/2520The element in subset S product is 3601/2520.
Therefore, we can calculate the product of the elements in S by solving the numbers using fractional addition.
Learn more about adding fractions here:
https://brainly.com/question/25412
#SPJ13
Answer:
Step-by-step explanation:
The answer should be 8/3.
A ball is dropped from a height of 10 ft. Assuming that on each bounce, the ball rebounds to one-fifth of its previous height, find the total distance traveled by the ball.
Answers
Answer: The ball is dropped from a height of 10 ft, so it first travels down 10 ft until it hits the ground. The distance traveled in this first part is 10 ft.
On the first bounce, the ball rebounds to one-fifth of its previous height, which is 2 ft (since 10/5 = 2). The ball then travels up 2 ft and back down 2 ft to the ground, for a total distance traveled of 10 + 2 + 2 = 14 ft.
On the second bounce, the ball rebounds to one-fifth of its previous height, which is 2/5 ft (since 2/5 x 2 = 4/5). The ball then travels up 4/5 ft and back down 4/5 ft to the ground, for a total distance traveled of 2/5 + 4/5 + 4/5 = 2 ft.
On the third bounce, the ball rebounds to one-fifth of its previous height, which is 4/25 ft (since 4/25 x 2/5 = 8/125). The ball then travels up 8/125 ft and back down 8/125 ft to the ground, for a total distance traveled of 4/25 + 8/125 + 8/125 = 0.32 ft (rounded to two decimal places).
The ball will continue to bounce, getting closer and closer to the ground with each bounce. We can calculate the total distance traveled by summing the distances traveled on each bounce:
10 + 14 + 2 + 0.32 + ...
To calculate the sum of this infinite series, we can use the formula for the sum of an infinite geometric series:
S = a / (1 - r)
where S is the sum, a is the first term, and r is the common ratio.
In this case, a = 10 (the distance traveled on the first drop), and r = 1/5 (the fraction by which the height decreases on each bounce). Plugging in these values, we get:
S = 10 / (1 - 1/5)
= 12.5
So the total distance traveled by the ball is 12.5 ft.
Step-by-step explanation:
Sam put $2,000 in a savings account at his bank. After 10 years, his account balance was $4,000. The interest rate on the savings deposit is blank %
Answers
The interest rate on the savings deposit is 10%.
The initial principal amount with Sam in the savings account at the bank is $2000. The time period for which the interest is earned is 10 years. The final amount he received in total was $4000. Let the interest rate be "R".
The interest is the difference between the final and the initial amount. Simple interest is a quick and straightforward way to calculate the interest on a loan. Simple interest is calculated by multiplying the daily interest rate by the principle multiplied by the number of days between payments.
I = A - P
I = $4000-$2000
I = $2000
We will now use the formula for simple interest.
I = (P*R*T)/100
2000 = (2000*R*10)/100
R = 10
To learn more about interest rate, visit :
https://brainly.com/question/13324776
#SPJ1
A school lunch program serves 13,000 students. The program orders 3,250 pounds of chicken for the students. Determine how many pounds of chicken each student can have.
Answers
Answer:
0.25 or 1/4
Step-by-step explanation:
easy - 3250 pounds divided by 13000 students
everyone will get 0.25 or 1/4 of a pound of chicken
hope this helps!!
Have a nice day!
Click an item in the list or group of pictures at the bottom of the problem and, holding the button down, drag it into the correct position in the answer box. Release your mouse button when the item is place. If you change your mind, drag the item to the trashcan. Click the trashcan to clear all your answers.
Indicate the equation of the given line in standard form.
The line that contains the point Q( 1, -2) and is parallel to the line whose equation is
y - 4 = 2/3 (x - 3)

Answers
Answer:
The equation of the line is;
3y = 2x-8
Step-by-step explanation:
Firstly, we need the to get the slope of the given line
To do this, we will write the equation of the line in the standard form
the standard form
is;
y = mx + b
where m is the slope and b is the y-intercept
y -4 = 2/3(x-3)
y -4 = 2x/3 - 2
y = 2x/3 -2 + 4
y = 2x/3 + 2
with respect to the given equation, the slope of the line is 2/3
Mathematically, when two lines are parallel, the slopes of the line are equal
So now, we want to find the equation of the line that has a slope of 2/3 and passes through the point (1,-2)
so;
y = 2x/3 + b
So substitute the values of (1,-2)
1 for x and -2 for y
-2 = 2/3(1) + b
-2 = 2/3 + b
b = -2 - 2/3
b = (-6-2)/3 = -8/3
So the equation of that line is;
y = 2/3x - 8/3
Multiply through by 3
3y = 2x - 8
A survey was conducted to see how many phone calls people made daily. The results are displayed in the table below:

Answers
From the given frequency table,
Frequency represents the number of people who made the calls.
Total number of people who made the calls = 16 + 11 + 5 + 3 + 1
= 36
Number of people who made less than 13 calls = 16 + 11 + 5
= 32
Number of people who made at least 9 calls = 5 + 3 + 1
= 9
Percentage of people who made at least 9 calls = \(\frac{\text{Number of people who made at least 9 calls}}{\text{Number of people who made the calls}}\times 100\)
= \(\frac{9}{36}\times 100\)
= 25%
Difference in the number of people who made the calls between 5-8 calls than 13-16 calls = 11 - 3 = 8
Learn more,
https://brainly.com/question/3414458
Solve: 4x < -16
A
B
C
D
X>4
X>12
X<-4
X <-20
Answers
Answer:
\( \: answer \: c = x < - 4\)
A student observes the phases of the moon over the course of 3 months and records observations with pictures each day.
Which option best explains whether or not this approach is an authentic scientific investigation?
This is an authentic investigation because the phases of the moon are changing each day.
This is not an authentic investigation because science requires that you follow the scientific method correctly.
This is an authentic investigation because science does not always have to follow the scientific method.
This is not an authentic investigation because it does not change any variables.
^_____^ (~ ̄▽ ̄)~ Please HeLp
Answers
That's great! Observing and recording the phases of the moon over several months can be an interesting project.
Capture the moon's image: Using a camera or smartphone, take a picture of the moon on a daily basis. Aim for clear and focused shots that capture the moon's details.
Present the findings: The student can create a report or presentation summarizing their project, including the methodology, observations, and conclusions. They may also include a selection of the most representative pictures to showcase the changes in the moon's appearance.
Remember, this project requires patience and consistency in taking pictures each day. By documenting the moon's phases over three months, the student will gain a deeper understanding of this celestial phenomenon and its cyclical nature.
To know more about several months:- https://brainly.com/question/205325
#SPJ11
The fox population in a certain region has a continuous growth rate of 5% per year. It is estimated that the population in the year 2000 was 10,100 foxes.
a) Find a function that models the population,P(t) , after (t) years since year 2000 (i.e. t= 0 for the year 2000).
b) Use your function from part (a) to estimate the fox population in the year 2008.
c) Use your function to estimate the year when the fox population will reach over 18,400 foxes. Round t to the nearest whole year, then state the year.
Answers
Answer:
P(t) = A * (1 + r)^t ;
14,922 ;
Year 2013
Step-by-step explanation:
Given the following :
Continuous growth rate(r) = 5% = 0.05
Population in year 2000 = Initial population (A) = 10,100
Time(t) = period (years since year 2000)
A)
Find a function that models the population,P(t) , after (t) years since year 2000 (i.e. t= 0 for the year 2000).
P(t) = A * (1 + r)^t
Trying out our function for t = year 2000, t =0
P(0) = 10,100 * (1 + 0.05)^0
P(0) = 10,100 * 1.05^0 = 10,100
B.)
Use your function from part (a) to estimate the fox population in the year 2008.
Year 2008, t = 8
P(8) = 10,100 * (1 + 0.05)^8
P(8) = 10,100 * 1. 05^8
P(8) = 10,100 * 1.4774554437890625
= 14922.29
= 14,922
c) Use your function to estimate the year when the fox population will reach over 18,400 foxes. Round t to the nearest whole year, then state the year.
P(t) = A * (1 + r)^t
18400 = 10,100 * (1.05)^t
18400/10100 = 1.05^t
1.8217821 = 1.05^t
1.05^t = 1.8217821
In(1.05^t) = ln(1.8217821)
0.0487901 * t = 0.5998151
t = 0.5998151 / 0.0487901
t = 12.293787
Therefore eit will take 13 years
2000 + 13 = 2013
2(a+7) - 7 = 9 what is the answer
Answers
Answer:
The answer is 1
Step-by-step explanation:
2(a+7)−7=9
Step 1: Simplify both sides of the equation.
2(a+7)−7=9
(2)(a)+(2)(7)+−7=9(Distribute)
2a+14+−7=9
(2a)+(14+−7)=9(Combine Like Terms)
2a+7=9
2a+7=9
Step 2: Subtract 7 from both sides.
2a+7−7=9−7
2a=2
Step 3: Divide both sides by 2.
2a
2
=
2
2
a=1
Put the steps in order to show how to solve the equation 4y - 7 = 25

Answers
Answer: E, A, D, C, B
Step-by-step explanation:
First, we need to get y alone. So we will add 7 to the side of the equation that has the 4y in it.
So the first one will be.
Add 7 to both sides of the equation.
Now the second one is
4y = 25 + 7 Because what you do to one side of the equation, you do to the other. So we add 7 to 25.
Then the 3rd one will be 4y = 32 because 25+7 is equal to 32. But we still have that 4y on the other side of the equation. So the next equation is 4y = 32.
The second to last step is Divide both sides by 4 because thats
how you isolate y. So once you divide both sides by 4. You will get 8. Leading you into the next and final step.
Y = 8
And thats how you do it!
Use the definition of Taylor series to find the Taylor series (centered at c ) for the function. f(x)=e 4x
,c=0 f(x)=∑ n=0
[infinity]
Answers
The answer is , the Taylor series (centered at c=0) for the function f(x) = e^(4x) is given by:
\($$\large f(x) = \sum_{n=0}^{\infty} \frac{4^n}{n!}x^n$$\)
The Taylor series expansion is a way to represent a function as an infinite sum of terms that depend on the function's derivatives.
The Taylor series of a function f(x) centered at c is given by the formula:
\(\large f(x) = \sum_{n=0}^{\infty} \frac{f^{(n)}(c)}{n!}(x-c)^n\)
Using the definition of Taylor series to find the Taylor series (centered at c=0) for the function f(x) = e^(4x), we have:
\(\large e^{4x} = \sum_{n=0}^{\infty} \frac{e^{4(0)}}{n!}(x-0)^n\)
\(\large e^{4x} = \sum_{n=0}^{\infty} \frac{4^n}{n!}x^n\)
Therefore, the Taylor series (centered at c=0) for the function f(x) = e^(4x) is given by:
\($$\large f(x) = \sum_{n=0}^{\infty} \frac{4^n}{n!}x^n$$\)
To know more about Function visit:
https://brainly.in/question/222093
#SPJ11
The Taylor series for f(x) = e^(4x) centered at c = 0 is:
f(x) = 1 + 4x + 8x^2 + 32x^3/3 + ...
To find the Taylor series for the function f(x) = e^(4x) centered at c = 0, we can use the definition of the Taylor series. The general formula for the Taylor series expansion of a function f(x) centered at c is given by:
f(x) = f(c) + f'(c)(x - c) + f''(c)(x - c)^2/2! + f'''(c)(x - c)^3/3! + ...
First, let's find the derivatives of f(x) = e^(4x):
f'(x) = d/dx(e^(4x)) = 4e^(4x)
f''(x) = d^2/dx^2(e^(4x)) = 16e^(4x)
f'''(x) = d^3/dx^3(e^(4x)) = 64e^(4x)
Now, let's evaluate these derivatives at x = c = 0:
f(0) = e^(4*0) = e^0 = 1
f'(0) = 4e^(4*0) = 4e^0 = 4
f''(0) = 16e^(4*0) = 16e^0 = 16
f'''(0) = 64e^(4*0) = 64e^0 = 64
Now we can write the Taylor series expansion:
f(x) = f(0) + f'(0)(x - 0) + f''(0)(x - 0)^2/2! + f'''(0)(x - 0)^3/3! + ...
Substituting the values we found:
f(x) = 1 + 4x + 16x^2/2! + 64x^3/3! + ...
Simplifying the terms:
f(x) = 1 + 4x + 8x^2 + 32x^3/3 + ...
Therefore, the Taylor series for f(x) = e^(4x) centered at c = 0 is:
f(x) = 1 + 4x + 8x^2 + 32x^3/3 + ...
To know more about Taylor series, visit:
https://brainly.com/question/32235538
#SPJ11
two essential features of all statistically designed experiments are
Answers
A comparison of multiple treatments and the use of the double-blind method are two fundamental components of all statistically designed experiments. (6) Compare various treatments; assign patients to treatments at random.
What is double-blind method?
A kind of clinical experiment in which neither the participants nor the researcher is aware of the treatment or intervention that each participant is receiving until the trial is complete.
This reduces the likelihood of skewed study outcomes.
What is a sample of a double-blind study?
Imagine, for instance, that researchers are looking into the effects of a novel medication.
The participants in a double-blind study would not be aware of who was receiving the real medication and who was receiving a placebo, and neither would the researchers who interact with them.
Learn more about double-blind study
brainly.com/question/4911918
#SPJ4
The complete question is -
Two essential features of all statistically designed experiments are (2 Points) O use enough subjects; always have a control groups O always have a placebo group; use the double - blind method O use a block design; use chance to assign subjects to treatments O compare several treatments; use the double - blind method O compare several treatments; use chance to assign subjects to treatments.
Correct answer brainlist
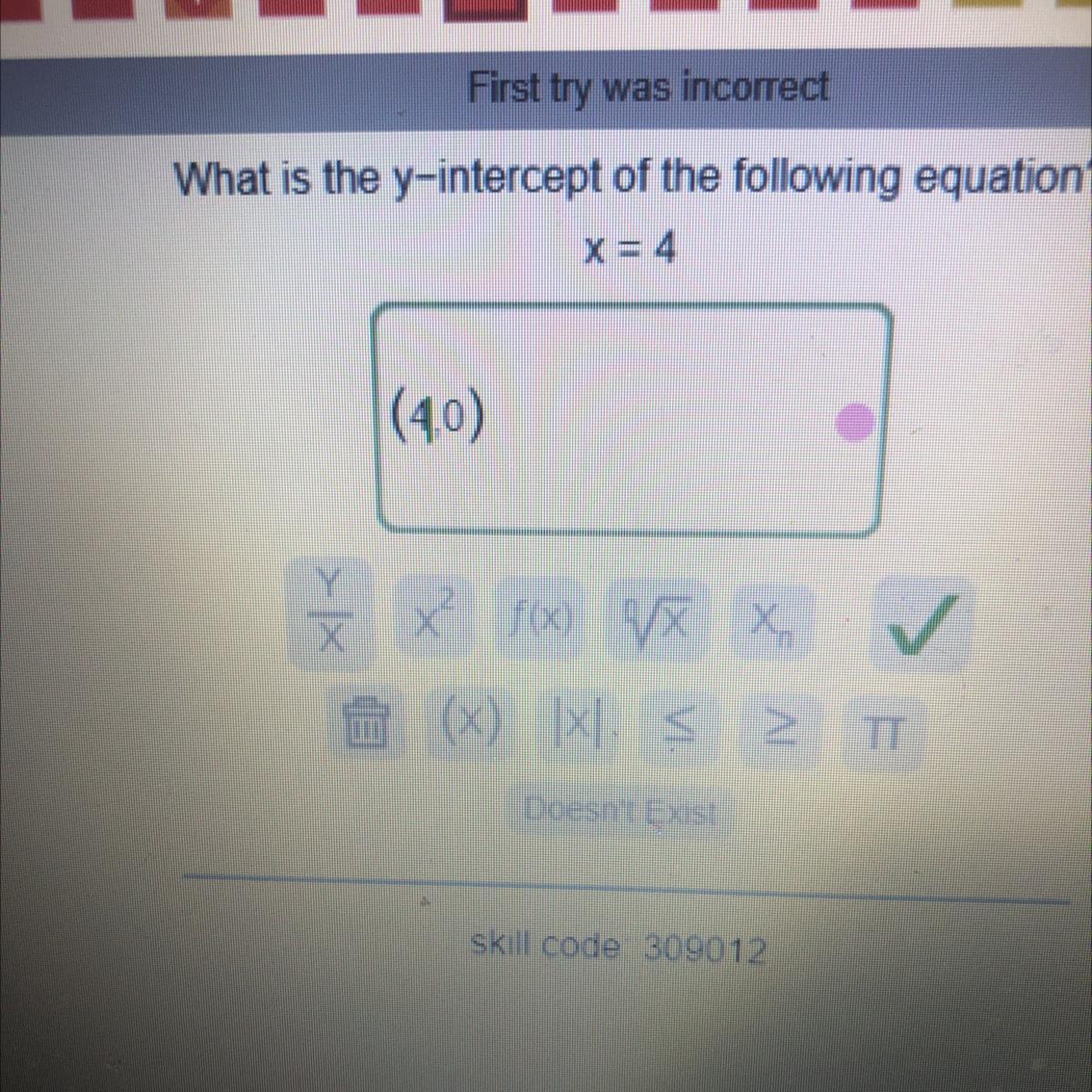
Answers
Answer:
easy y/x is the answer for you answer
zeros are also called roots, x-intercepts, and solutions. question 1 options: true false
Answers
The given statement "Zeros are also called roots, x-intercepts, and solutions" is true.
Zeros, roots, x-intercepts and solutions are all the same and interchangeable terms. These terms are used to describe the value of x for which a function's value is 0. Zeros of a function are called roots because they are solutions to the equation f(x) = 0.
They are called x-intercepts because the x-axis is the line where the value of y is 0, and so the zeros occur at the points where the graph intersects the x-axis. Finally, they are called solutions because finding the zeros of a function is equivalent to solving the equation f(x) = 0. In conclusion, all these terms are synonymous with each other, meaning that they refer to the same thing, the value(s) of x for which the function's value is zero.
Learn more about x-intercepts here:
https://brainly.com/question/14180189
#SPJ11
The points in the table lie on a line. Find the slope of the line.
Х
6
--2
2.
6
y
8
5
2
1

Answers
Answer:
\( Slope (m) = -\frac{3}{4} \)
Step-by-step explanation:
Using any two pairs from the table of values given, (-2, 5) and (2, 2):
\( Slope (m) = \frac{y_2 - y_1}{x_2 - x_1} \)
Where,
\( (-2, 5) = (x_1, y_1) \)
\( (2, 2) = (x_2, y_2) \)
Plug in the value into the slope formula:
\( Slope (m) = \frac{2 - 5}{2 -(-2)} \)
\( Slope (m) = -\frac{3}{4} \)
What is the value of x?
Original 9 inches - 6 feet
Enlargement 12 inches - x feet
Answers
Answer:
Step-by-step explanation:
