Write an expression for 3 more than twice the number n.
Please answer my question
Answers
Answer:
2n+3
Step-by-step explanation:
Related Questions
4
÷
3
8
=
4 ÷
8
3
=
Answers
4 / 38 = 2/19
Alternative answer = 0.105
Question 2:
4 / 83 = 4/83
Alternative answer = 0.048
Answer: Question 1:
4 / 38 = 2/19
Alternative answer = 0.105
Question 2:
4 / 83 = 4/83
Alternative answer = 0.048
Step-by-step explanation:
x - y = 3
b) Work out the value of 2x – 2y
Answers
Step-by-step
Explanation:
Lexi is creating beaded jewelry to give to her family and friends. For her family, she assembled 5 bracelets and 9 necklaces, using a total of 922 beads. For her friends, she assembled 9 bracelets and 5 necklaces, using a total of 786 beads. Assuming she uses a consistent number of beads for every bracelet and necklace, how many beads is she using for each?
Answers
The number of Lexi is using for every bracelet and necklace include the following:
For her bracelet =329
For her necklace= 593
What is addition?Addition is defined as one of the arithmetic parameters that can be used to combine various data together to arrive at a particular value.
For the family,
bracelet = 5
necklace = 9
Total jewelry made = 14
total number of beads used = 922 beads
The number of beads used for bracelet;
= 5/14×922
= 4610/14
= 329
The number of beads used for necklace;
= 9/14× 922
= 8298/14
=593
Learn more about addition here:
https://brainly.com/question/28772449
#SPJ1
What is the domain of the function represented by the graph?

Answers
Answer:
It's either A or D.......
what is 1/5 x 5 1/3? help please
Answers
Answer:
1 1/15
Step-by-step explanation:
(I think)
And I am not a very good explainer
(sorry)
Please answer quickly thanks
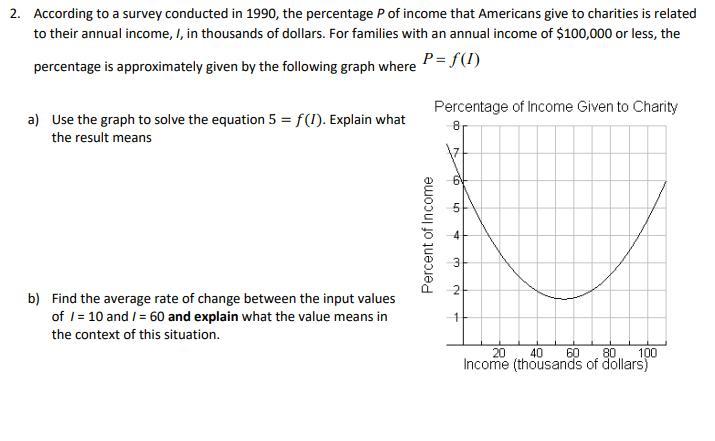
Answers
The meaning of 5 = f(I) is that the 5% have an income of $6000
The average rate is that %0.054 per thousand of dollars
How to determine the solution to the graphFrom the question, we have the following parameters that can be used in our computation:
The graph
The equation is given as
5 = f(I)
This means that:
We find x when f(I) = 5
Using the graph, we have
x = 6
This means that the income is $6000
The average rate of changeThis is calculated as
Rate = (f(x2) - f(x1))/(x2 - x1)
Substitute the known values in the above equation, so, we have the following representation
Rate = (1.8 - 4.5)/(10 - 60)
Evaluate
Rate = 0.054
Read more about average rate at
https://brainly.com/question/17131025
#SPJ1
What is the meaning of "all free variables of a formula ϕ(u1, . . . , un) are among u1, . . . , un"?

Answers
The phrase "all free variables of a formula ϕ(u1, . . . , un) are among u1, . . . , un" refers to a property of a logical formula ϕ with variables u1, u2, ..., un. In logic and formal systems, variables are used to represent unspecified elements or objects.
What does the phrase imply?When a variable is considered "free" in a formula, it means that it is not bound by any quantifiers or other logical operators in the formula. In other words, it is a variable that is not restricted in any way within the formula.
The given statement implies that all the free variables in the formula ϕ(u1, . . . , un) are explicitly listed among the variables u1, u2, ..., un. In other words, the formula ϕ does not contain any additional free variables beyond the ones explicitly mentioned.
Learn more about variable on
https://brainly.com/question/28248724
#SPJ1
Unions, intersections, and complements involving 2 sets
Sets B and C are subsets of the universal set U.
These sets are defined as follows.
U={f, k, m, s, x, y, z)
B={k, s, y}'
C={s,z}
(a) B'UC' = 1
(b) B'nc =
Answers
Intersection of B'∩C = {k, y}
To find the intersection of B' and C, we need to first find the complement of set B (B') and then find the intersection between B' and C.
1. Complement of set B (B'):
The complement of set B (B') consists of all elements in the universal set U that are not in set B. From the given information, set B is defined as {k, s, y}', which means it contains all elements in U except for k, s, and y. Therefore, the complement of set B is {f, m, x, z}.
2. Intersection between B' and C:
Now, we need to find the intersection between B' (complement of B) and set C. From the given information, set C is defined as {s, z}. To find the intersection, we need to identify the common elements between B' and C.
The elements present in both B' and C are k and y. Therefore, the intersection of B' and C is {k, y}.
So, the answer to (b) is B'∩C = {k, y}.
For more such questions on Intersection, click on:
https://brainly.com/question/30915785
#SPJ8
Calculate the circumference of a circle with a radius of 8 inches.
Answers
To calculate the circumference of a circle, you can use the formula:
\(\displaystyle C=2\pi r\)
Where \(\displaystyle C\) represents the circumference and \(\displaystyle r\) represents the radius of the circle.
Given that the radius \(\displaystyle r\) is 8 inches, we can substitute this value into the formula:
\(\displaystyle C=2\pi (8)\)
Simplifying the expression:
\(\displaystyle C=16\pi \)
Thus, the circumference of a circle with a radius of 8 inches is \(\displaystyle 16\pi \) inches.
Note: \(\displaystyle \pi \) represents the mathematical constant pi, which is approximately equal to 3.14159.
\(\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}\)
♥️ \(\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}\)
please help me ASAP!!!
Answers
The correct answer is the third option, because:
\(\sqrt[]{50}=\sqrt[]{25\times2}=\sqrt[]{25}\sqrt[]{2}=5\sqrt[]{2}\)Laxman and Virat together can complete a piece of work in 8 days and Laxman alone can complete it in 12 days in how many days would Bharat alone complete the work
Answers
Answer:
14 days
Step-by-step explanation:
Black Cab Taxi charges a $4.95 flat rate for a ride in the cab. In addition to that, they charge $0.49 per mile. Katie has no more than $20 to spend on a ride. At most, how many miles can Katie travel without exceeding her spending limit?
Answers
Answer:
30 miles.
Step-by-step explanation:
.5x + 5 > 20
x = 30
Please give brainliest if this helped you!
24-5₂
Sorry i tried to put the 2 at the top edge of the 5 but i could not.
Answers
\\Workhelp2gow//.com
An Eastbound train (E) traveling 95 mph and a Westbound train (W) traveling 110 mph leave the same train station at different times. After 4 hours, they are 4 00 miles apart. Which system of linear equations can be used to determine the time that each of the trains has been traveling?
Answers
Answer:
The system of linear equations that can be used to determine the time that each of the trains has been traveling is:
E + W = 4 ....... Equation 1
95 E + 110W = 400 ......Equation 2
Hence,
An Eastbound train has been travelling for = (E) = 2.67 hours
A Westbound train has been travelling for = (W) = 1.33 hours
Step-by-step explanation:
An Eastbound train (E) traveling 95 mph and a Westbound train (W) traveling 110 mph leave the same train station at different times. After 4 hours, they are 4 00 miles apart. Which system of linear equations can be used to determine the time that each of the trains has been traveling?
Speed = Distance/Time
Distance = Speed × Time
Let the time
An Eastbound train = (E)
A Westbound train = (W)
E + W = 4 hours ....... Equation 1
95mph × E + 110mph × W = 400 miles
95 E + 110W = 400 miles ......Equation 2
The system of linear equations that can be used to determine the time that each of the trains has been traveling is:
E + W = 4 ....... Equation 1
95 E + 110W = 400 ......Equation 2
E = 4 - W
We substitute 4 - W for E in Equation 2
95 (4 - W) + 110W = 400
380 - 95W + 110W = 400
Collect like terms
95W - 110W = 400 - 380
15W = 20
W = 20/15
W = 1.3333333333 hours
≈ 1.33 hours
E = 4 - W
E = 4 - 1.33 hours
E = 2.67 hours
Therefore,
An Eastbound train has been travelling for = (E) = 2.67 hours
A Westbound train has been travelling for = (W) = 1.33 hours
5 times 100 times 105
Answers
Answer:
52500
Step-by-step explanation:
first do 5*105 to get 525 then mutiply by 100 to get 52500
Please help. How can i find the volume of cylinder
THE # are the blue and grey

Answers
The volume of the cylinder would be 2120.6\(units^3.\)
To find the volume of a cylinder, you need to use the formula:
Volume = π x \(radius^2\) x height
Where π (pi) is a mathematical constant approximately equal to 3.14159, radius is the distance from the center of the cylinder to its edge, and height is the distance from one end of the cylinder to the other.
To apply this formula, you need to know the values of the radius and height of the cylinder. Once you have these values, simply substitute them into the formula and solve for the volume.
For example, if the radius of a cylinder is 5 units and the height is 27 units, the volume of the cylinder would be:
Volume = π x \(radius^2\)x height
Volume = 3.14159 x\(5^2\)x 27
Volume = 2120.6 \(units^3\)
Therefore, the volume of the cylinder would be 2120.6\(units^3.\)
for such more question on volume of the cylinder
https://brainly.com/question/6204273
#SPJ11
Find the area of the shape shown below.

Answers
Answer:
Total Area = 26.75
Step-by-step explanation:
Remark
The hardest triangle to see is the top one. So we'll start with it.
It has a vertical leg of 3.5 and a horizontal one of 2 + 2 + 5 = 9
Top Triangle Area
Area = 1/2 base * height
Area = 1/2 * 9 * 3.5
Area = 15.75
Triangle on the lower left
Area = 1/2 * 2 * 2
Area = 2
Square on lower middle
Area = 2*2
Area = 4
Triangle on lower right area
Area = 1/2 * 2 * 5
Area = 5
Total Area
Total Area = 5 + 4 + 2 + 15.75
Total Area = 26.75
(1990). (2010)
Mean- 150.32. Mean-125.57
Median-117.17. Media - 123.17
SD - 12.23. SD- 7.01
Some information about auto theft rates (number of auto thefts per 100,000 population) for a sample of 178 cities in two different years is
summarized below. Express this statistical information in words. What changes were there in the overall shape of the variation of this variable? In central tendency? In dispersion?
Answers
The statistical information is that in 1990, there was 150 auto theft per population over 178 cities.
Interpreting the statistical informationThe information also shows that 50% of the cities had a theft rate of less than 117 per population while the reaming 50% of the cities had a rate above that level.
A standard deviation of 12 means that individual cities could have had crime rates as low as 114 and as high as 186.
In 2010, the crime rate over 178 cities averaged 125 per I lakh population. The remaining half had a theft rate of less than 123 while the reaming half recorded a rate above that level.
A standard deviation of 7 means that individual cities could have had crime rates as low as 104 and as high as 146.
On a comparative note, both the average and standard deviation recorded a significant reduction. The standard deviation experienced a huge reduction of more than 40%. This means that the combined measure came down from 8.14% in 1990 to 5.6% in 2010.
The shape of the distribution depicts a sizable shift to the left along with an appreciable compression of the spread.
Learn more about population on:
https://brainly.com/question/25896797
Order the values from least to greatest. -27 = 93/2 = 274/3 981
Answers
To order the values from least to greatest find the values the expressions are equal to
\(\sqrt[3]{-27}=-3\)\(9^{\frac{3}{2}}=\sqrt[]{9^3}=27\)\(27^{\frac{4}{3}}=\sqrt[3]{27^4}=81\)\(\sqrt[4]{81}=3\)order the numbers from least to greatest based on what they are equal to when simplified
\(\sqrt[3]{-27}<\sqrt[4]{81}<9^{\frac{3}{2}}<27^{\frac{4}{3}}\)The area of a rectangle is 16 1/3 square inches.The width is 4 2/3. Inches.Find the length
Answers
Answer:
Let the length of the rectangle be L. Then we can use the formula for the area of a rectangle:
Area = Length x Width
Substituting the given values, we get:
16 1/3 = L x 4 2/3
To solve for L, we can first convert the mixed numbers to improper fractions:
16 1/3 = 49/3
4 2/3 = 14/3
Substituting these values, we get:
49/3 = L x 14/3
To solve for L, we can multiply both sides by the reciprocal of 14/3:
49/3 ÷ 14/3 = L
Simplifying, we get:
L = 49/3 x 3/14
L = 7/1
L = 7
Therefore, the length of the rectangle is 7 inches.
Step-by-step explanation:
What formula do I use for this? How do I get the points to graph?

Answers
The graph of the function y = 5|x - 4| is added as an attachment
Sketching the graph of the functionFrom the question, we have the following parameters that can be used in our computation:
y = 5|x - 4|
The above function is an absolute value function that has been transformed as follows
Vertically stretched by a factor of 5Shifted right by 4 unitsNext, we plot the graph using a graphing tool by taking not of the above transformations rules
The graph of the function is added as an attachment
Read more about functions at
brainly.com/question/2456547
#SPJ1

Becky can wash 14 dishes in 5 minutes.How many dishes will she be able to wash in 8 minutes?
Answers
Answer:
find how many dishes she can wash in 1 minute:
14 divided by 5
2.8/per min
Find 8-minutes:
8 times 2.8
22.4 dishes
Please help me!!!!!!

Answers
Answer:
y = -\(\frac{7}{4}\)x + 14
Step-by-step explanation:
if we transpose the correct answer will be y = -\(\frac{7}{4}\)x + 14
Damien has enough red paint to cover an area of 36 square meters
Answers
Answer:
1.91
Step-by-step explanation:
If is wrong i'm sorry
Step-by-step explanation:
He has 3600 litres of paint
EspanolOwners of a recreation area are filling a small pond with water. They are adding water at a rate of 32 liters per minute. There are 700 liters in the pond to start.Let W represent the total amount of water in the pond (in liters), and let T represent the total number of minutes that water has been added. Write an equationrelating W to T. Then use this equation to find the total amount of water after 19 minutes.Equation: 0хTotal amount of water after 19 minutes: [liters5?
Answers
We know that
• The rate is 32 liters per minute.
,• There are 700 liters to start.
Notice that 700 liters are the initial condition of the problem, that means 700 is going to be the independent term of our linear equation. Additionally, the rate of 32 liters per minute is the coefficient of the x. So, the equation that models this situation is
\(y=32x+700\)Now, to find the total amount of water after 19 minutes, we have to use x=19 in the equation
\(y=32(19)+700=608+700=1308\)Therefore, after 19 minutes the total amount of water is 1,308 liters.A ratio of two angles is 5 to 3 and their sum is 180 degrees. Find the measure of each angle. The find their complements. Make a sketch, set up the corresponding equation and solve it.
Answers
Answer:
112.5
67.5
Step-by-step explanation:
We know the ratio is:
5:3
So, we can write it as:
5x+3x=180, with 5x being one angle, and 3x being the other
combine like terms
8x=180
divide both sides by 8
x=22.5
5(22.5)=112.5
3(22.5)=67.5
So, one angle is 112.5 and the other is 67.5.
Hope this helps!
If a seed is planted, it has a 70% chance of growing into a healthy plant.
If 8 seeds are planted, what is the probability that exactly 4 don't grow?
Answers
Answer:
Thus, the probability that exactly 4 don't grow is 0.1361 or 13.61%
Step-by-step explanation:
Binomial Distribution
Consider a random experience that has only two possible outcomes: Success or Failure. Let's call p to the probability that the event has a successful outcome and q to the failure outcome.
It follows that p+q=1, or q=1-p.
Now repeat the random experience n times. We want to calculate the probability of getting x successful outcomes. This can be done with the Binomial Distribution formula:
\(\displaystyle P_{x} = {n \choose x}\cdot p^{x}\cdot q^{n-x}\)
Where :
\(\displaystyle {n \choose x}\)
Is the number of combinations, calcula ted as follows:
\(\displaystyle {n \choose x} =_nC_x=\frac{n !}{x ! (n-x) !}\)
A planted seed has a 70% chance of growing into a healthy plant. The successful outcome has p=0.7 and q=0.3.
The experience is repeated n=8 times. We want to calculate the probability of having 4 failures (not growing seeds) or x=4 successes.
Apply the formula:
\(\displaystyle P_{4} = {8 \choose 4}\cdot 0.7^{4}\cdot 0.3^{8-4}\)
\(\displaystyle P_{4} = 70\cdot 0.7^{4}\cdot 0.3^{4}\)
\(\displaystyle P_{4} = 0.1361\)
Thus, the probability that exactly 4 don't grow is 0.1361 or 13.61%
Goran is running for president of the chess club, and he received 24 votes. There are 40 members in the club. What percentage of the club members voted for Goran?
Answers
Answer:
60%
Step-by-step explanation:
\(\sf Percentage=\left(\dfrac{Value}{Total\:value}\right) \times 100\)
Given:
value = 24 votesTotal value = 40 membersSubstituting these into the formula:
\(\implies \sf \left(\dfrac{24}{40}\right) \times 100=0.6 \times 100 = 60 \%\)
Therefore, 60% of the club members voted for Goran.
Line c has an equation of y= 4/3x + 9. Line d is parallel to line c and passes through (-4,-4). What is the equation of line d?
Answers
The equation of the line that is parallel to y = 4/3x + 9 is: y = 4/3x + 4/3.
What is the Equation of Parallel Lines?Parallel lines are lines that do not intercept each other and also have the same slope value.
In an equation in slope-intercept form, y = mx + b, the slope of the line is represented as the value of m.
This means that two lines that are parallel to each other will have the same slope (m).
The slope of line c, y = 4/3x + 9, is 4/3. The slope of line d will also be m = 4/3.
Find the y-intercept (b) by substituting m = 4/3 and (x, y) = (-4, -4) into y = mx + b:
-4 = 4/3(-4) + b
-4 = -16/3 + b
-4 + 16/3 = b
4/3 = b
b = 4/3
Substitute m = 4/3 and b = 4/3 into y = mx + b:
y = 4/3x + 4/3.
Learn more about the equation of parallel lines on:
https://brainly.com/question/11345748
#SPJ1
Describe the relationship among the four terms