Write an equation in slope-intercept form to represent the total cost, y, of leasing a car for x months.
months costs
1 $1,859
3 $2,577
8 $4,372
12 $5,808
Answers
Answer:
\(y=359x+1500\)
Step-by-step explanation:
The data provided is as follows:
Months (x) Costs (y)
1 $1,859
3 $2,577
8 $4,372
12 $5,808
The slope intercept form is:
\(y = mx+b\)
Here,
m = slope
b = intercept.
Compute the value of m and b as follows:
\(\begin{aligned} b &= \frac{\sum{Y} \cdot \sum{X^2} - \sum{X} \cdot \sum{XY} }{n \cdot \sum{X^2} - \left(\sum{X}\right)^2} = \frac{ 14616 \cdot 218 - 24 \cdot 114262}{ 4 \cdot 218 - 24^2} \approx 1500 \\ \\m &= \frac{ n \cdot \sum{XY} - \sum{X} \cdot \sum{Y}}{n \cdot \sum{X^2} - \left(\sum{X}\right)^2} = \frac{ 4 \cdot 114262 - 24 \cdot 14616 }{ 4 \cdot 218 - \left( 24 \right)^2} \approx 359\end{aligned}\)
The equation in slope-intercept form to represent the total cost, y, of leasing a car for x months is:
\(y=359x+1500\)
Related Questions
A 10% increase in cigarette prices has been found to result in a _____ decrease of smokers. a. 2% b. 4% c. 10% d. 20% please select the best answer from the choices provided. a b c d
Answers
A 10% increase in cigarette prices has been found to result in a 4% decrease of smokers.
What is the effect of price increase in the demand for cigarettes?An increase in cigarette price will result in a decrease in the demand for cigarettes.
Since more money needs to be spent to but the same product, less consumers can be able to afford it.
Therefore, a 10% increase in cigarette prices has been found to result in a 4% decrease of smokers.
Learn more about increase in price at: https://brainly.com/question/26526671
#SPJ4
The football team has a total of 50 jerseys. There are 20 medium-sized jerseys. What percent of the jerseys are medium-sized jerseys?
Answers
Answer:40%
Step-by-step explanation:20 divided by 50 is 0.4 then multiply that by 100 and get 40
Answer:
Well the equation for this would 50*.20 = ...
The first half of the answer would be 10.
BUT!
You need to subtract 10 from 50.
50-10 = 40!
There you go.
Step-by-step explanation:
what is the correct solution for the arithmetic expression (2 8)/2*9/3 using the order of operations employed by oracle 12c when solving equations?
Answers
The correct solution to the arithmetic expression (2 8)/2*9/3 using the order of operations as employed by Oracle 12c when solving equations is 4.
According to the Order of Operations, the first step is to evaluate expressions inside parentheses, then perform any multiplications or divisions, and finally perform any additions or subtractions. In this expression, the first step would be to evaluate the expression inside the parentheses: (28)/2. This evaluates to 14.
Next, the expression becomes 14 * 9/3. According to the Order of Operations, we need to perform the multiplication first, so 14 * 9 = 126. Finally, we perform the division: 126/3 = 42.
So, the correct solution to the expression (2 8)/2 * 9/3 is 42.
Order of operations is a set of rules used to determine the sequence in which arithmetic operations should be performed in a mathematical expression to obtain the correct result. The rules ensure that operations are performed in a consistent and predictable manner.
The order of operations is typically represented by the acronym PEMDAS, which stands for Parentheses, Exponents, Multiplication and Division (from left to right), and Addition and Subtraction (from left to right).
Learn more about order of operations here:
https://brainly.com/question/27529825
#SPJ4
The figure is made up of a hemisphere and a cylinder. What is the exact volume of the figure? Enter your answer in the box. in³ 8 in. 6 in.

Answers
The volume of the given shape is required.
The required volume is 90π in³.
Volumed = Diameter = 6 inchesr = Radius = \(\frac{d}{2}\) = \(\frac{6}{2}\) = 3 inchesh = Height = 8 inchesThe given figure is made of a hemisphere and cylinder
Volume of a cylinder is given by \(\pi \text{r}^2\text{h}\)
Volume of a hemisphere is given by \(\dfrac{2}{3} \pi \text{r}^3\)
The total volume is
\(\text{V}= \pi \text{r}^2\text{h}+\sf \dfrac{2}{3} \pi \text{r}^3\)
\(\rightarrow\text{V}= \pi \text{r}^2 \ \huge \text (\sf h+\sf \dfrac{2}{3} {r}\huge \text)\)
\(\sf \rightarrow\text{V}= \pi \times3^2 \ \huge \text (\sf 8+\sf \dfrac{2}{3} \times3\huge \text)\)
\(\sf \rightarrow\text{V}= \bold{\underline{90\pi }}\)
Learn more about volume at:
https://brainly.com/question/27033747
Convert 3.95 to a simplified fraction
Answers
Answer:
3 and 19/20
Step-by-step explanation:
3.95 = 395/100 = 79/20 = 3 19/20
Answer:
3 and 19/20
Step-by-step explanation:
3.95 = 3 + 0.95. 3 stays how it is. 0.95 = 95/100 as a fraction. Common factor of 5, divide on top and bottom. You get 19/20. Add back the 3. You get 3 and 19/20
If g(x) = 1-2x, find each value.
Find g (-12)
Find g (0)
Find -5 g (4) - 1
Answers
Answer:
25 , 1 , 34
Step-by-step explanation:
substitute x = - 12 into g(x)
g(- 12) = 1 - 2(- 12) = 1 + 24 = 25
substitute x = 0 into g(x)
g(0) = 1 - 2(0) = 1 - 0 = 1
substitute x = 4 into g(x)
- 5(1 - 2(4)) - 1 = - 5(1 - 8) - 1 = - 5(- 7) - 1 = 35 - 1 = 34
How do I find the length of WU?

Answers
The length of WU is 7.615, which can be found by using the Pythagorean Theorem.
The length of WU can be found by using the Pythagorean Theorem. The Pythagorean Theorem states that the square of the length of the hypotenuse of a right triangle is equal to the sum of the squares of the lengths of the other two sides. In this case, the hypotenuse is WU and we know the length of the other two sides, which are 7 (side VU) and 3 (side UT). Substituting these values into the Pythagorean Theorem, we get \(WU^2 = 7^2 + 3^2\). Solving this equation, we get WU = √58 = 7.615. Therefore, the length of WU is 7.615.
Learn more about Pythagorean Theorem here:
https://brainly.com/question/14930619
#SPJ1
Functions or Not a Function? Explain?

Answers
The x table increases by a constant amount, 1. While the y table increases by different amounts, making it not a function.
also if you graphed this, it would not be a line, making it not a function.
Hope this helped!! :)
Answer:
function
Step-by-step explanation:
To be a function, each value of the x-coordinate can be used only once. In other words, all x-coordinates must be different.
Here, the x-coordinates are all different, so it is a function.
A shoemaker sold a pair of for $245.99 if the buyer a $300.00 bill, how much will the buyer receive in change?
*two decimal places don't forget your $ sign. Example: $50.00 NOT 50*
Answers
Answer:
$54.01
Step-by-step explanation:
All you have to do is $300.00-$245.99 .
Find the area of this circle. Use
3.14 for .
5 ft
The area of the circle is about 12.
(Round to the nearest hundredth as needed.)

Answers
Answer:
78.5
Step-by-step explanation:
This graph shows how fast the International Space Station travels in orbit
around Earth
What is the meaning of the point with an x-coordinate of 2?
Speed of Space Station
10
14
12
10
Distance (miles)
2
2 4 8 10 12 14 16
Time (seconds)
O A. The space station travels 2 miles in 10 seconds,
O B. In 1 second, the space station travels 2 miles.
C. It takes the space station 5 seconds to go 10 miles,
OD. In 2 seconds, the space station travels 10 miles,
Answers
Answer:
D
Step-by-step explanation:
what is the correct ratio to find x?
a. tan(x) = 1/2
b. tan(x) = √5/5
c. tan(x) = √15/3
d. tan(x) = 2√5/3

Answers
The correct trigonometric ratio to find the angle of the right triangle is tan x = 1 / 2.
How to find the angle of a triangle?A right angle triangle is a triangle with one of its angles as 90 degrees. The sides and angles of a triangles of a triangle can be found using trigonometric ratios as follows:
The sides of a right angle triangle can be named base on the angles position. They include adjacent side, hypotenuse sides and opposite side.
Therefore, let's find x using tangential ratio as follows;
tan x = opposite / adjacent
opposite side = 5
adjacent side = 10
Therefore,
tan x = 5 / 10
tan x = 1 / 2
learn more on right triangle here: https://brainly.com/question/3770177
#SPJ1
According to the national weather service, the mean daily temperature in stuart is 72.1°, f with a standard deviation of 3.7° f. consider the mean daily temperature in stuart for a sample of 86 randomly selected days.
Answers
The probability that the mean daily temperature of a sample of 100 randomly selected days is greater than the mean daily temperature by at least 1.7°F is 0.002 .
Let the mean daily temperature be = x',
The mean daily temperature in Stuart is (μ) = 72.2,
The standard deviation is (σ) = 5.9,
The sample size is (n) = 100,
⇒ μₓ = μ = 72.2 ,
⇒ σₓ = σ/√n = 5.9/√100 = 0.59,
So, the required probability is written as :
⇒ P(x' - μ ≥ 1.7)
⇒ P( (x'-μ)/σₓ ≥ 1.7/0.59)
⇒ P( Z ≥ 2.8813) = 0.00198
≈ 0.002.
Therefore, the required probability is 0.002.
Learn more about Probability here
https://brainly.com/question/13984715
#SPJ4
The given question is incomplete, the complete question is
According to the National Weather Service, the mean daily temperature in Stuart is 72.2°F with a standard deviation of 5.9°F. Consider the mean daily temperature in Stuart for a sample of 100 randomly selected days.
Determine the probability that the mean daily temperature of a sample of 100 randomly selected days is greater than the mean daily temperature by at least 1.7°F.
look at screenshot for question

Answers
Answer:
I think it is the first one as you add the 4 like from the other
[BRAINLIEST] a. Nick deposits money in a Certificate of Deposit account (CD). The balance (in dollars) in his account t years after making the deposit is given by N(t)=400(1.06)tfor t ≥ 0. Explain, in terms of the structure of the expression for N(t), why Nick's balance can never be $399.
Answers
Answer:
(1.06)0 = 1 and positive powers of 1.06 are larger than 1, thus the minimum value N(t) attains, if t≥0, is 400.
From the point of view of the context, a CD account grows in value over time so with a deposit of $400 the value will never drop to $399.
Tan?cos? Sin? What is the m

Answers
Answer:
45º
Step-by-step explanation:
Since we know the relatiionship of a 45-45-90 degree triangle, we can go two ways. Either we can use this to find CA and get the tangent of (6/6) or we can go straight to it. The hypotenuse in a 45-45-90 is always 6√2 and we know it is a right triangle so we can confirm this. So, measure of angle B is 45º.
Please answer CORRECTLY !!!!!! Will mark brainliest !!!!!!
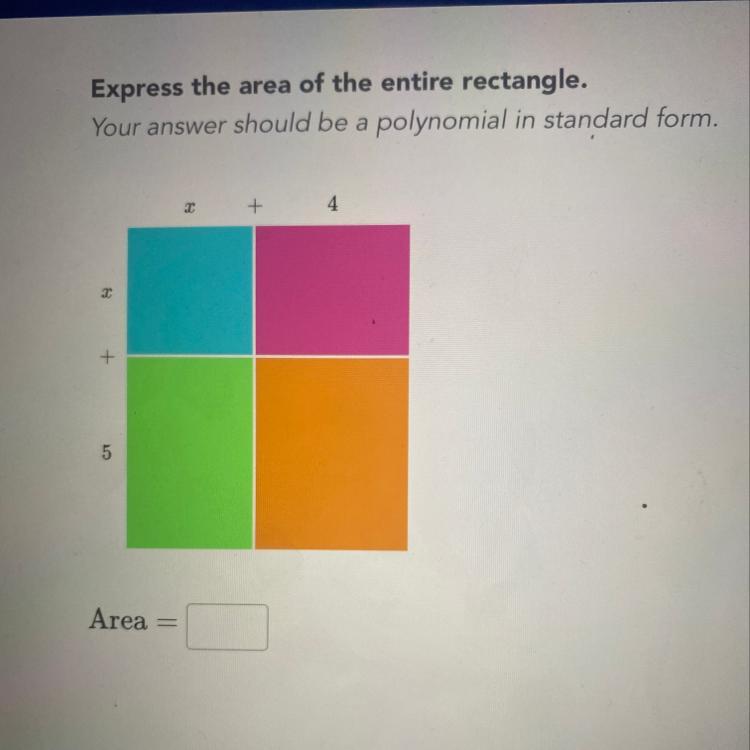
Answers
Answer:
x^2+9x+20
Step-by-step explanation:
what has to be the same in order to add fractions?
Answers
Explanation: you can’t add 3/12 and 2/6. You would have to change it to 3/12 + 4/12.
Sims waist is 30 inches. He wants to put on more weight and is hoping to gain enough weight to increase his waist size by 8%. How many inches does he want his waist to be?
Answers
Answer:
32.4 inches
Step-by-step explanation:
Sam wants the increase to be 8% of 30 inches.
IncreaseThe amount of increase Sam wants in his waist size is ...
8% × 30 in = 0.08×30 in = 2.4 in
Waist sizeAdding the wanted increase to his present size would make Sam's waist size be ...
30 in + 2.4 in = 32.4 in
Sam wants his waist size to be 32.4 inches.
__
Additional comment
The larger size can also be computed from ...
30 +8%×30 = (1 +8%)×30 = 1.08×30 = 32.4 . . . inches
ariana was looking at rent costs for 5 55 apartments. each rent was a different amount between $ 1 , 000 $1,000dollar sign, 1, comma, 000 and $ 1 , 400 $1,400dollar sign, 1, comma, 400 per month, except for one apartment whose rent was $ 4 , 800 $4,800dollar sign, 4, comma, 800 per month. [hide data] ariana looked at the mean and median of the rents. then, she decided to remove the $ 4 , 800 $4,800dollar sign, 4, comma, 800 rent from the set and recalculate the mean and median. how will removing this rent affect the mean and median? choose 1 answer: choose 1 answer:
Answers
If Ariana removes the $4,800 rent from the set, the mean and median of the remaining rents will decrease because $4,800 is a very high value compared to the other rents.
Before removing the $4,800 rent, the mean can be calculated by adding up all the rents and dividing by the total number of rents (5):
Mean = (1,000 + 1,200 + 1,300 + 1,400 + 4,800) / 5 = 2,540
The median is the middle value in the set, which is 1,300.
After removing the $4,800 rent, the new mean can be calculated by adding up the remaining rents and dividing by the new total number of rents (4):
New Mean = (1,000 + 1,200 + 1,300 + 1,400) / 4 = 1,225
The new median is still 1,300 because it is the middle value in the remaining set.
Therefore, removing the $4,800 rent will decrease both the mean and median of the remaining rents.
To know more about mean and median:
https://brainly.com/question/28670966
#SPJ4
A weight is attached to the end of a frictionless spring, pulled down to extend the
spring, and then released. Let d be the distance of the weight above the floor at
time t, where d is in centimeters and t is in seconds. The distance varies
sinusoidally over time.
A stopwatch reads 0.5 seconds when the weight reaches its first high point 42
centimeters above the floor, and the next low point 11 centimeters above the floor,
occurs at 1.2 seconds.
Write a trigonometric equation to express d in terms of t, and use your equation to
determine the weights distance from the floor at 4 seconds. Round to the nearest
centimeter.
Answers
A trigonometric equation to express d in terms of t is d = A sin(Bt - C) + D, the weight is approximately 16 centimeters above the floor at 4 seconds.
The distance, d, of the weight above the floor at time t can be expressed as a sinusoidal function of the form:
d = A sin(Bt - C) + D
where A is the amplitude, B is the frequency, C is the phase shift, and D is the vertical shift.
We are given that the weight reaches its first high point (maximum) at 0.5 seconds, which means that the phase shift is 0.5 seconds. At this point, d = 42 centimeters, which means that the amplitude is 42/1 = 42 centimeters.
We are also given that the next low point (minimum) occurs at 1.2 seconds, which means that the function has completed one full period between 0.5 and 1.2 seconds. Therefore, the period of the function is:
T = 1.2 - 0.5 = 0.7 seconds
The frequency, B, is the reciprocal of the period:
B = 1/T = 1/0.7 ≈ 1.43
Finally, we need to find the vertical shift, D. At time t = 0, the weight is at its equilibrium position, which is the midpoint between the maximum and minimum heights:
D = (42 + 11)/2 = 26.5
Putting all of this together, we get:
d = 42 sin(1.43(t - 0.5)) + 26.5
To find the weight's distance from the floor at 4 seconds, we simply need to plug in t = 4 into the equation and round to the nearest centimeter:
d = 42 sin(1.43(4 - 0.5)) + 26.5 ≈ 16 centimeters
To learn more about equation click on,
https://brainly.com/question/10720961
#SPJ1
1. If f(x) = (3x-2)/(2x+3), then f'(x) =
Answers
Answer:
\(f'(x)= \frac{13}{(2x+3)^2}\\\)
Step-by-step explanation:
\(f(x)= \frac{3x-2}{2x+3} \\\)
\(f'(x)=\frac{dy}{dx} = \frac{d}{dx}(\frac{3x-2}{2x+3})\\ f'(x)= \frac{(2x+3)\frac{d}{dx}(3x-2)-(3x-2)\frac{d}{dx}(2x+3) }{(2x+3)^{2} } \\f'(x)= \frac{(2x+3)(3)-(3x-2)(2)}{(2x+3)^{2} } \\\)
\(f'(x)= \frac{6x+9-6x+4}{(2x+3)^{2} }\\ f'(x)= \frac{13}{(2x+3)^2}\\\)
HELP ME PLEASE. THIS IS MY LAST QUESTION THEN I CAN GO TO BED.

Answers
Answer:
100.
Step-by-step explanation:
The 2 smaller triangles are similar, so:
48 / (x - 64) = 64 / 48
64(x - 64) = 48^2
x - 64 = 48^2/64
x = 48^2/64 + 64
= 100.
Explain in your own words why a constant has a degree of zero
Answers
Answer:
See below
Step-by-step explanation:
Because a constant never changes. It stays constant (it's in the word)! The function never changes since the slope is 0, therefore there's no vertical change.
Answer:
Step-by-step explanation:
The function value never changes and is always graphed as a horizontal line so theirs slopes become zero. This means there is no change that is vertical within and throughout the function.
Helped by the ONE & ONLY #QUEEN aka #DRIPPQUEENMO!!
HOPE THIS HELPED!!
Alana sold 6 oranges for $3. Write the equation that represents the price for any number of oranges.
Answers
Answer:
50 cents ($0.50)
Step-by-step explanation:
We need to find the price for one orange. To get one orange, you have to divide 6 by 6. Anything you do to one side of the equation must be done to the other side. You have to divide 3 by 6. If you do this, you get .5, or 1/2. In money, that translates to 50 cents.
Hope this helps!
Step-by-step explanation:
the price of one orange is indeed 3/6 = 1/2 = $0.50.
the equation residential the price for any number of oranges contains then a variable, say x, to stand for the number of purchased oranges :
p(x) = 0.5x
meaning that the price of x oranges is 0.5×x.
the reading on the thermometer reads 10°C and the temperature rises 30°C what will the new reading be
Answers
Answer:
40c
Step-by-step explanation:
it starts at 10c and goes up 30c you can just add 30 to 10 to get 40
The solution is, 40°C will be the new reading.
What is addition?
Addition is a way of combining things and counting them together as one large group. ... Addition in math is a process of combining two or more numbers.
here, we have,
given that,
the reading on the thermometer reads 10°C
and the temperature rises 30°C
now, we have to add the temperature ,
so, the new reading will be,
30+10
=40°C
Hence, The solution is, 40°C will be the new reading.
To earn more on addition click:
brainly.com/question/29560851
#SPJ2
Let f(x) = 2x^3+3x -1.
(a) Explain why has at most one real root.
(b) Explain why has a root in the interval .
(c) Starting from an initial input of , use two iterations of Newton's Method to approximate the real root of .
Answers
(a) The function f(x) = 2x^3+3x-1 has at most one real root because its discriminant is positive, which means it has two complex roots and one real root at most.
(b) The function f(x) = 2x^3+3x-1 has a root in the interval [0,1] because f(0) is negative and f(1) is positive, and the intermediate value theorem guarantees the existence of a root between these values.
(c) Using two iterations of Newton's method starting with an initial guess of x_0 = 0.5, we can approximate the real root of f(x) to be x = 0.414217
(a) The function f(x) is a polynomial of degree three, which means it can have at most three roots. However, not all three roots need to be real. In this case, we can use the discriminant of the polynomial to determine the number of real roots. The discriminant is given by b^2 - 4ac, where a = 2, b = 3, and c = -1. Plugging these values into the formula, we get:
b^2 - 4ac = 3^2 - 4(2)(-1) = 17
Since the discriminant is positive, the polynomial has two complex roots and one real root at most.
(b) To show that the polynomial has a root in the interval [0,1], we can evaluate f(0) and f(1) and show that they have opposite signs. This is known as the intermediate value theorem. We have
f(0) = 2(0)^3 + 3(0) - 1 = -1
f(1) = 2(1)^3 + 3(1) - 1 = 4
Since f(0) is negative and f(1) is positive, there must be a root of f(x) in the interval [0,1].
(c) To use Newton's method to approximate the root of f(x), we need to start with an initial guess. Let's use x_0 = 0.5. The formula for Newton's method is
x_(n+1) = x_n - f(x_n)/f'(x_n)
We need to compute f(x_n) and f'(x_n). We have
f(x_n) = 2(x_n)^3 + 3(x_n) - 1
f'(x_n) = 6(x_n)^2 + 3
Plugging in x_0 = 0.5, we get
f(x_0) = 2(0.5)^3 + 3(0.5) - 1 = 0.375
f'(x_0) = 6(0.5)^2 + 3 = 4.5
Using these values in the Newton's method formula, we get
x_1 = x_0 - f(x_0)/f'(x_0) = 0.5 - 0.375/4.5 = 0.416666...
We can repeat the process with x_1 as the new guess
f(x_1) = 2(0.416666...)^3 + 3(0.416666...) - 1 = 0.007716...
f'(x_1) = 6(0.416666...)^2 + 3 = 4.238425...
Plugging these values into the formula, we get
x_2 = x_1 - f(x_1)/f'(x_1) = 0.416666... - 0.007716.../4.238425... = 0.414217...
Learn more about function here
brainly.com/question/29197921
#SPJ4
The units digit of a two-digit number is four more than the tens digit. If the number is doubled, it will be 1 more than the reversed number. Find the number.
Answers
Answer:
The number is 37
Step-by-step explanation:
The given parameters are;
The unit digit of a two-digit number = 4 + The tens digit
2 × The two-digit number = 1 + The reversed number
Let x represent the unit digit and y represent the tens digit, we have;
x = 4 + y
2 × yx = xy + 1
Which gives;
2 × yy+4 = 2y2y+8
xy + 1 = 4 + yy + 1
y + 1 = 2y + 8 - 10 (we assume that the product of 2 and the unit digit is more than 10 so we subtract 10 from the product to equate the unit digits of the two numbers
10 + 1 - 8 = 2y - y
10 - 7 = y
y = 3
x = y + 4 = 3 + 4 = 7
x = 7
Therefore, the number = 37.
Answer:
37
Step-by-step explanation:
Falling rock on another planet was detected as moving at the following speeds, corresponding to the time suggested in the table, which equation Can be used to find the speed of the rock at T seconds?

Answers
Answer:
B. s = 24t
Step-by-step explanation:
Since s varies directly with t, therefore, equation that will represent the relationship would take the form of s = my
m = rate of change
✔️Find the rate of change:
Rate of change using two given pairs, (0.5, 12) and (2.5, 60),
Rate of change (m) = ∆s/∆t = (60 - 12)/(2.5 - 0.5) = 48/2 = 24
✔️Substitute m = 24 into s = mt
s = 24t
Convert 2.9% to a decimal.
Answers
Answer: 0.029
Step-by-step explanation:
2.9/100
= 0.029
Answer:
Step-by-step explanation:
2.9% in a decimal is 0.029