Write an equation in slope intercept form of the line that passes through the given points (-5,-11) and (6,11)
*** somebody please hurry and answer this for me,i have until tomorrow to get this done for my final grade.***
Answers
Considering the expression of a line, the equation of the line that passes through the pair of points (-5,-11) and (6,11) is y=2x -1.
Linear equationA linear equation o line can be expressed in the form y = mx + b
where
x and y are coordinates of a point.m is the slope.b is the ordinate to the origin and represents the coordinate of the point where the line crosses the y axis.Knowing two points (x₁, y₁) and (x₂, y₂) of a line, the slope m of said line can be calculated using:
m= (y₂ - y₁)÷ (x₂ - x₁)
Substituting the value of the slope m and the value of one of the points in the expression y = mx + b, the value of the ordinate to the origin b can be obtained.
Equation in this caseIn this case, being (x₁, y₁)= (-5, -11) and (x₂, y₂)= (6,11), the slope m can be calculated as:
m= (11 - (-11))÷ (6 - (-5))
m= (11 +11)÷ (6 + 5)
m= 22÷ 11
m= 2
Considering point 2 and the slope m, you obtain:
11= 2×6 + b
11= 12 +b
11 -12= b
-1= b
Finally, the equation of the line is y=2x -1.
Learn more about the equation of a line having 2 points:
brainly.com/question/16137599
brainly.com/question/2503591
#SPJ1
Related Questions
B = 75*
C = 50*
A = ?*

Answers
Answer: A = 55* or 55 degrees
Step-by-step explanation:
The interior angles of a triangle always have a sum of 180 degrees.
75 + 50 + x = 180
Solve for x
FInal answer: 55 degrees
hope i explained it :)
Evaluate the following path integrals integral_C f(x, y, z) ds, under the following conditions. (Note that exp(u) = e^u.) (a) f(x, y, z) = exp(Squareroot z), and c: t rightarrow (4, 1, t^2), t elementof [0, 1] (b) f(x, y, z) = yz, and c: t rightarrow (t, 3t, 4t), t elementof [1, 3]
Answers
(a) The path integral is 2/3 (exp(1) - 1).
(b) The path integral is 108 sqrt(26).
(a) In order to evaluate the path integral for the first case, we first need to parameterize the curve C. Since the curve is given in terms of x, y, and z, we can parameterize it by setting x=4, y=1, and z=t^2, so that the curve becomes:
C: t -> (4, 1, t^2), t ∈ [0, 1]
Now we can evaluate the path integral using the formula:
∫_C f(x, y, z) ds = ∫_a^b f(x(t), y(t), z(t)) ||r'(t)|| dt
where r(t) = (x(t), y(t), z(t)) is the parameterization of the curve C, and ||r'(t)|| is the magnitude of its derivative. In this case, we have:
r(t) = (4, 1, t^2)
r'(t) = (0, 0, 2t)
||r'(t)|| = 2t
So the path integral becomes:
∫_C f(x, y, z) ds = ∫_0^1 exp(Squareroot t^2) 2t dt
We can simplify this expression using the substitution u = t^2, du = 2t dt:
∫_C f(x, y, z) ds = ∫_0^1 exp(Squareroot t^2) 2t dt = ∫_0^1 exp(u^(1/2)) du
Now we can evaluate the integral using integration by substitution:
∫_C f(x, y, z) ds = [2/3 exp(u^(3/2))]_0^1 = 2/3 (exp(1) - 1)
So the final answer for the path integral is 2/3 (exp(1) - 1).
(b) In this case, the curve C is given by:
C: t -> (t, 3t, 4t), t ∈ [1, 3]
To evaluate the path integral, we use the same formula as before:
∫_C f(x, y, z) ds = ∫_a^b f(x(t), y(t), z(t)) ||r'(t)|| dt
where r(t) = (x(t), y(t), z(t)) is the parameterization of the curve C, and ||r'(t)|| is the magnitude of its derivative. In this case, we have:
r(t) = (t, 3t, 4t)
r'(t) = (1, 3, 4)
||r'(t)|| = sqrt(1^2 + 3^2 + 4^2) = sqrt(26)
So the path integral becomes:
∫_C f(x, y, z) ds = ∫_1^3 (3t)(4t) sqrt(26) dt = 12 sqrt(26) ∫_1^3 t^2 dt
We can evaluate the integral using the power rule:
∫_C f(x, y, z) ds = 12 sqrt(26) [(1/3) t^3]_1^3 = 108 sqrt(26)
So the final answer for the path integral is 108 sqrt(26).
To know more about path integral refer here :
https://brainly.com/question/31059631#
#SPJ11
Expand.
Your answer should be a polynomial in standard form.
-p^2(p^2-p-1)=
Answers
Answer:
Step-by-step explanation:
Use distributive property. Then use exponent law.
Exponent law used here = \(a^{m}*a^{n}=a^{m+n}\)
\(-p^{2}(p^{2} - p - 1) = -p^{2}*p^{2} - p *(-p^{2}) - 1*(-p^{2}) \\\\= -p^{4} + p^{3}+p^{2}\)
need help on this please giving brainlest! :)

Answers
can someone please help me I only have a few minutes

Answers
Answer:
(x + 8)(y - 3)
Step-by-step explanation:
Since you have a few minutes left, I will make this quick.
Focus on one letter within the trapezoid ABCD. Pick a certain letter that can correlate to trapezoid A'B'C'D'.
If we move B to B', we would notice it takes 8 skips,therefore (x + 8). If we do the same for y, we would notice it takes 3 skips down. Therefore (y - 3)

4. Let X=(A,B,C,D,E,F,G), where
A={b,f,h},
B={b,h},
C={a,b,c,d,g},
D={c,d,e,f,g},
E={b,e,f},
F={e,f,h},
1 (a) Draw a bipartite graph G such that the problem of finding a transversal of X is equivalent to the problem of finding a matching in G. (b) Find a transversal of X, or show that it doesn't have one.
Answers
(a) A bipartite graph G can be constructed where one set of vertices represents the elements of X and the other set represents the subsets of X. The problem of finding a transversal of X is equivalent to the problem of finding a matching in G.
(b) A transversal of X can be found by analyzing the constructed bipartite graph G and identifying a matching, or it can be shown that no transversal exists.
(a) To create a bipartite graph G, we consider one set of vertices to represent the elements of X (A, B, C, D, E, F, G), and another set of vertices to represent the subsets of X (A, B, C, D, E, F, G). Each vertex in the element set is connected to the vertices in the subset set if the element belongs to that subset. For example, vertex A is connected to vertices A, C, and D, as A is present in subsets A, C, and D.
(b) In order to find a transversal of X, we need to find a matching in the bipartite graph G. A matching in a bipartite graph is a set of edges where no two edges share a common vertex. By identifying such a matching in G, we can determine a transversal of X.
To find a matching, we can employ various algorithms like the Hopcroft-Karp algorithm or the Ford-Fulkerson algorithm. These algorithms will traverse the bipartite graph and identify a set of edges that form a matching.
If it is not possible to find a matching, it indicates that no transversal exists for X. This means that there is no subset in X that contains exactly one element from each of the other subsets. In such cases, we can conclude that X does not have a transversal.
In summary, by constructing a bipartite graph G and finding a matching in it, we can solve the problem of finding a transversal of X. If a matching exists, it represents a transversal, while the absence of a matching indicates the absence of a transversal.
Learn more about bipartite graph
brainly.com/question/32702889
#SPJ11
On September 1, you own 12.5 shares of stock that are worth $149.87. On
December 1, the shares are worth $94.87. What was the change in the price per
share of stock?
Answers
From September 1 to December 1 is three months apart so meaning the price dropped $49.95 for the months of Oct to Dec.
The required change in the price of the share of stock is $4.4.
Given that,
On September 1, you own 12.5 shares of stock that are worth $149.87. On December 1, the shares are worth $94.87, and the change in the price per share of stock is to be determined.
The process in mathematics to operate and interpret the function to make the function or expression simple or more understandable is called simplifying and the process is called simplification.
Here,
Initial total cost shares of stock = $149.87
A total number of shares = 12.5
The initial cost of single share = 149.87/ 12.5 = $11.98
Now final cost of the total share = $94.87
The final cost of the single share is = 94.87 / 12.5 = $7.58
Change in price of shares of stock = 11.98 - 7.58 = $4.4
Thus, the required change in the price of the share of stock is $4.4.
Learn more about simplification here: https://brainly.com/question/12501526
#SPJ6
Translate the following statement into an algebraic expression Use x for your variable. The sum of the cube of a number and seven times the number.
Answers
Answer:
\(x^{3} + 7x\)
Step-by-step explanation:
cube of a number is the number multiplied by itself thrice.
This means:
x × x × x = \(x^{3}\)
Seven times (multiply, ×) the number(x) means:
7 × x = \(7x\)
We are to sum (add, +) both:
\(x^{3}\) + \(7x\)
Answer is \(x^{3}\) + \(7x\)
an experiment requires a measurement before and after the presentation of a stimulus to 20 subjects. in the analysis of the data collected from this experiment, how many degrees of freedom are there in the test?
Answers
In a repeated measures design with 20 subjects, each subjected to 2 measurements (before and after stimulus presentation), the degrees of freedom in the test would be 19.
DF in Repeated Measures ExperimentThe problem is about an experiment in which a measurement is taken before and after a stimulus is presented to 20 subjects. The aim is to determine the number of degrees of freedom in the data analysis of the experiment.
Degrees of freedom (df) are a measure of the amount of variability in a set of data that is free to vary in the calculation of a statistical test. In a repeated measures design, the degrees of freedom are calculated as the number of subjects minus 1. In this case, with 20 subjects, the degrees of freedom would be 19.
The concept of degrees of freedom is used in both mathematics and physics, but the specific context of a t-test for dependent samples is commonly used in statistical analysis, particularly in the social sciences, psychology, and education research. So, it is more related to mathematics.
Learn more about DF in Repeated Measures Experiment here:
https://brainly.com/question/13226419
#SPJ4
Describe the long run behavior of f(x)=5(2)x+1:
As x→−[infinity], f(x) =
As x→[infinity], f(x) =
Answers
The long run behavior of the function f(x)=5(2)x+1 is that it approaches 1 as x approaches negative infinity and it approaches infinity as x approaches positive infinity.
The long-term behavior of the function f(x)=5(2)x+1 can be discovered by examining how the function behaves as x gets closer to negative and positive infinity.
As x→−[infinity], f(x) = 5(2)^ -∞+1 = 5(0)+1 = 1
As x approaches negative infinity, the value of the function approaches 1.
As x→[infinity], f(x) = 5(2)^ ∞+1 = 5(∞)+1 = ∞
As x approaches positive infinity, the value of the function approaches infinity.
As a result, the function f(x)=5(2)x+1 behaves in the long run in such a way that it approaches 1 as x approaches negative infinity and infinity as x approaches positive infinity.
Learn more about behavior at https://brainly.com/question/22443880
#SPJ11
What is √45 rounded to the nearest whole number
Answers
decimal form: 6.70820393…
nearest whole number: 7
Answer:
3√5
Step-by-step explanation:
In any one-minute interval, the number of requests for a popular Web page is a Poisson random variable with expected value 180 requests.a A Web server has a capacity of C requests per minute. If the number of requests in a one-minute interval is greater than C, the server is overloaded. Use the central limit theorem to estimate the smallest value of C for which the probability of overload is less than 0.055. Note that your answer must be an integer. Also, since this is a discrete random variable, don't forget to use "continuity correction". C= b Now assume that the server's capacity in any one-second interval is âC/60â, where âxâ is the largest integer â¤x. (This is called the floor function.) For the value of C derived in part (a), what is the probability of overload in a one-second interval? This time, don't approximate via the CLT, but compute the probability exactly.
Answers
Poisson distribution of number of requests for a popular Web page,
a) Web server has a capacity of C requests per minute is equals to the 206.
b) The probability of overload in a one-second interval is approximately equal to 1.
Let x denotes the number of requests for a popular web page. Now, X = number of requests per minute ~ Poisson (180)
Now, by central limit theorem the distribution of x can be approximated by Normal diet with mean = 180 and variance 180 and we denote the approximated variable by Y, that is \(Y \: \tilde \: \: N(180, 180)\).
If number of requests in a one minute interval is greater than C, then probability of overload is less than 0.055, that is P[ X > C] < 0.055
P[ X > C] ~ P[ Y > C + 0.5] ( by continuity )
so, P[ Y > C + 0.5] < 0.055
\(P[ \frac{ Y - 180}{ \sqrt{180}} > \frac{C + 0.5 - 180}{ \sqrt{180} }] < 0.055\)
According to normal distribution, \( P[ \frac{ Y - 180}{180} ] = Z ≃N(1,0)\)
Therefore, \(P[ Z > \frac{C + 0.5 - 180}{ \sqrt{180} }] < 0.055\)
=> \([\frac{C + 0.5 - 180}{ \sqrt{180} }] < Z_{0.055}\)
= 0.478069 ~ 0.4781.
=> \(C - 199.5 < 0.4781 × \sqrt{ 180} \)
=> C = 199.5 + 0.4781 × 13.4164
=> C = 205.91 ~ 206.
b) Now, we have to determine the probability of overload in a one-second interval, using the value of C obtained in part(a), so, C = 206 so, [ C/60] = 3
Probability of overload, P = P( X> 3)
= 1 - P( X≤ 3)
\(= 1 - \sum_{x = 0}^{3} e^{-180} \frac{ 180^x}{x!} \)
= 1
Hence, required probability is 1.
For more information about Possion distribution, visit:
https://brainly.com/question/30890396
#SPJ4
Triangle X Y Z is shown. The length of X Z is 12, the length of Y Z is 11, and the length of Y X is 6.
A scalene triangle has the lengths 6, 11, and 12. Keyla uses the law of cosines to find the measure of the largest angle. Complete her work and find the measure of angle Y to the nearest degree.
1. 122 = 112 + 62 − 2(11)(6)cos(Y)
2. 144 = 121 + 36 − (132)cos(Y)
3. 144 = 157 − (132)cos(Y)
4. −13 = −(132)cos(Y)
degrees
Answers
Answer:
84 degrees
Step-by-step explanation:
Applying the Cosine Rule (Choice 2 is the correct one) :-
12^2 = 11^2 + 6^2 - 2*11*6 cos Y
144 = 121 + 36 - 132 cos Y
cos Y = (121 + 36 - 144) / 132
cos Y = 0.09848
Y = 84.3 degrees
in a survey of college students, 855 said that they have cheated on an exam and 1717 said that they have not. if one college student is selected at random, find the probability that the student has cheated on an exam.
Answers
The probability that a college student selected at random has cheated on an exam is 0.3328 or 33.28% .
The given problem requires us to find the probability that a student has cheated on an exam given that the number of college students who have cheated on an exam is 855 and the number of students who have not cheated on an exam is 1717.
The total number of students is the sum of those who have cheated and those who have not cheated.
The probability of an event happening is given by the formula:P(A) = Number of outcomes favorable to event A / Total number of possible outcomesLet C be the event that a college student has cheated on an exam.Number of outcomes favorable to event C = 855Total number of possible outcomes = Number of students who have cheated on an exam + Number of students who have not cheated on an exam
= 855 + 1717
= 2572
Therefore, the probability that a college student selected at random has cheated on an exam is:
P(C) = Number of outcomes favorable to event C / Total number of possible outcomes
= 855 / 2572
= 0.3328 or 33.28% (approx.)
Hence, the probability that the student has cheated on an exam is 0.3328 or 33.28% (approx.).
To know more about probability refer here:
https://brainly.com/question/30034780
#SPJ11
Which expression is equivalent to the following complex fraction?
3
-4
x-1
2.
X-1
2-
0
2(X-2)
-4X+7
-4X+7 D.
2(X-2)
4x+7
2(x2-2)
2(x2-2)
4x+7

Answers
Answer:
\(\frac{-4x+7}{2(x-2)}\)
Step-by-step explanation:
\(For x \neq 1 \\\frac{\frac{3}{x-1}-4}{2-\frac{2}{x-1}}=\frac{\frac{3}{x-1}-\frac{4x-4}{x-1}}{\frac{2x-2}{x-1}-\frac{2}{x-1}}=\frac{\frac{-4x+7}{x-1}}{\frac{2x-4}{x-1}}=\frac{-4x+7}{2(x-2)}\)
The equivalent expression is 2(x - 2) / (-4x + 7).
Option A is the correct answer.
What is an expression?An expression contains one or more terms with addition, subtraction, multiplication, and division.
We always combine the like terms in an expression when we simplify.
We also keep all the like terms on one side of the expression if we are dealing with two sides of an expression.
Example:
1 + 3x + 4y = 7 is an expression.
3 + 4 is an expression.
2 x 4 + 6 x 7 – 9 is an expression.
33 + 77 – 88 is an expression.
We have,
To simplify the given expression:
[3/(x - 1) - 4] / [2 - 2/(x - 1)]
We need to find a common denominator for the two fractions in the numerator and denominator of the main fraction.
The common denominator for the numerator is (x - 1) and for the denominator is 2(x - 1).
We can then rewrite the expression as:
[3 - 4(x - 1)/(x - 1)] / [2(x - 1) - 2/(x - 1)]
Simplifying the numerator by distributing the -4:
(3 - 4x + 4) / (x - 1)
(-4x + 7) / (x - 1)
Now, simplifying the denominator by finding a common denominator:
2(x - 1) - 2/(x - 1)
= (2x - 2 - 2)/(x - 1)
= 2(x - 2)/(x - 1)
Substituting back into the original expression, we get:
(-4x + 7)/(x - 1) / [2(x - 2)/(x - 1)]
Multiplying by the reciprocal of the denominator:
(-4x + 7)/(x - 1) x (x - 1)/[2(x - 2)]
(-4x + 7)/[2(x - 2)]
Therefore,
The equivalent expression is 2(x - 2) / (-4x + 7).
Learn more about expressions here:
https://brainly.com/question/3118662
#SPJ5
i need help fast!!!!

Answers
Answer:
1st choice: 1/4(y - 10) = 2/3
Step-by-step explanation:
the "variable" is y
"is" means "=" (equals sign)
one fourth = 1/4
"difference of" means subtract
Answer: 1/4(y - 10) = 2/3
find a vector a with representation given by the directed line segment ab−→−, where a(−6,0,1) and b(1,6,−2) .
Answers
vector representation of the given vectors will be AB(5,6,-3).
What is vector, explain by giving example?A quantity or phenomena with independent qualities for both size and direction is called a vector. The word can also refer to a quantity's mathematical or geometrical representation. Velocity, momentum, force, electromagnetic fields, and weight are a few examples of vectors in nature.
The vector representation will be -
A(x1,x2,x3), B(x1,x2,x3) so, AB will be - (x2 - x1, y2 - y1, z2 - z1)
So, given,
A(−6,0,1)
B(1,6,−2)
AB(1+6, 6-0, -2-1)
AB (5,6,-3)
To learn more about vector representation from given link
https://brainly.com/question/14409307
#SPJ4
Please help me find the area of compound shapes?!??!

Answers
Answer:
27cm²
Step-by-step explanation:
Chop the irregular shape into two rectangles!
(I divided by the inner corner next to the 5cm mark across to the side with no label at all on the left)
6x2=12 (longer rectangle)
5x3=15 (shorter rectangle)
12+15=27cm²
I hope this helps! :)
What property is illustrated in the following equation?
8 + 5 = 5 + ?
Answers
The answer is communitive property.
Answer: 3
Step-by-step explanation: Did it recently.
How many nickels would you need to make a stack 100 inches tall.
Answers
Answer:
1303 would be about the number of nickels would you would need to make a stack 100 inches tall
PLS HELP ASAP ILL GIVE BRAINLIEST

Answers
Answer: the first option
Step-by-step explanation:
The answer of a multiplication problem is the “product” and since it’s 7 times n squared, the answer is a product. Making it the first option
Find the missing angle measurement in each set of supplementary angles.
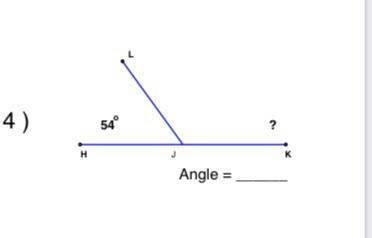
Answers
Answer:
126°
Step-by-step explanation:
180-54 = 126
Supplementary angles form 180°. Let's take the missing angle as 'x'.
54° + x° = 180°
x = 180° - 54°
x = 126°
=》 Angle LJK = 126°
______
RainbowSalt2222 ☔
What’s the answer to this simpflied?

Answers
Multiply x(x^2+2x+4) and -2(x^2+2x+4)
Combine like terms:
Final answer:
Answers
x^3-8
hope this helps!!

please help thanks :)

Answers
The equation of line A and line B will be y =4 and x = 8, respectively.
What is the linear system?A linear system is one in which the parameter in the equation has a degree of one. It might have one, two, or even more variables.
We know the equation of the line parallel to the x-axis.
y = c
The equation of line A will be
y = 4
We know the equation of the line parallel to the y-axis.
x = c
The equation of line B will be
x = 8
More about the linear system link is given below.
https://brainly.com/question/20379472
#SPJ1
help meeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeee

Answers
Answer: 2.5, 5.3
Step-by-step explanation:
\(-16t^2 +126t=217\\ \\ 16t^2 -126t+217=0\\\\t=\frac{-(-126) \pm \sqrt{(-126)^2 -4(16)(217)}}{2(16)}\\\\t \approx 2.5, 5.3\)
a man finds 1 hundred dollars and he keeps one half of it, gives 1 fourth if it to someone and and gives another 1 fifth of it to some else and he puts the rest in savings. how much did he give everyone
Answers
is (n x (n +1)) / 2 the same as (n/2)(n+1)
Answers
Answer:
nope
Step-by-step explanation:
simplify the first equation
Answer:
yes
Step-by-step explanation:
The associative and commutative properties of multiplication allow you to rearrange the product to the form shown in the question.
Division by 2 is effectively multiplication by 1/2.
\((n\times(n+1))/2\qquad\text{given}\\\\=\dfrac{n(n+1)}{2}=\dfrac{n}{2}(n+1)\\\\=\boxed{(n/2)(n+1)}\)
__
Additional comment
Evaluation of the expressions according to the order of operations will proceed differently for the two expressions.
For the first expression, evaluation steps are ...
add 1 to nmultiply the sum by ndivide the product by 2For the second expression, evaluation steps are ...
divide n by 2add 1 to nmultiply the results of these two operationsAs we said above, the properties of multiplication ensure the results are the same either way.
As a practical matter, for integer values of n, one of n and (n+1) will be even. It is usually convenient to divide the even number by 2. This means the evaluation might be ...
((n+1)/2)n . . . . for odd n(n+1)(n/2) . . . . for even nFor certain computer representations of the numbers, results may differ depending on the specific numbers and the order of evaluation.
Can anyone answer at least one of these?

Answers
Answer:
1=
216
Step-by-step explanation:
6x9x4
216
Answer:
1. 24cm² 2. 2x + 5 3. 12 4. 30m²
Step-by-step explanation:
1. 4 × 6 = 24
2. (14x² + 35x)/7x = 2x + 5
3. (\(d_{1}\) × 16)/2 = 96
=> \(d_{1}\) × 16 = 192
=> \(d_{1}\) = 12
4. 24 ÷ 2 = 12
\(\sqrt{13^{2} - 12^{2}}\) = \(\sqrt{25}\) = 5
5 × 12/2 = 30



It takes an ant farm 3 days to consume 1/2 of an apple
At that rate, how many days will it take the ant farm to consume 3 apples?
Answers
Answer:
18 days
Step-by-step explanation:
You need to decide how many times 3 apples are more than ½: 3 / ½ = 6
So it will take 6 times more time: 3 x 6 = 18 days.