write an equation for the line that passes through the points (-1,-12) and (4,8)
Answers
Answer:
y = 4x - 8
Step-by-step explanation:
(-1, -12) & (4, 8)
First you want to find the slope of the line that passes through these points. To find the slope of the line, we use the slope formula: (y₂ - y₁) / (x₂ - x₁)
Plug in these values:
(8 - (-12)) / (4 - (-1))
Simplify the parentheses.
= (8 + 12) / (4 + 1)
= (20) / (5)
Simplify the fraction.
20/5
= 4
This is your slope. Plug this value into the standard slope-intercept equation of y = mx + b.
y = 4x + b
To find b, we want to plug in a value that we know is on this line: in this case, I will use the second point (4, 8). Plug in the x and y values into the x and y of the standard equation.
8 = 4(4) + b
To find b, multiply the slope and the input of x(4)
8 = 16 + b
Now, subtract 16 from both sides to isolate b.
-8 = b
Plug this into your standard equation.
y = 4x - 8
This is your equation.
Check this by plugging in the other point you have not checked yet (-1, -12).
y = 4x - 8
-12 = 4(-1) - 8
-12 = -4 - 8
- 12 = -12
Your equation is correct.
Hope this helps!
Related Questions
Which of the following represents the eighth root of x to the fifth power in exponential form? (6 points)
5x^8
8x^5
x to the five eighths power x^(5/8)
x to the eight fifths power x^(8/5)

Answers
Answer:
\(x^{\frac{5}{8}}\)
Step-by-step explanation:
8th root of x to the power fifth. This means the power will be 5/8
\(x^{\frac{5}{8}}\)Your choice is correct .
4 x 5-10 - 2 (1-2) + 5=
Answers
Answer:
\(17\)
Step-by-step explanation:
\(4\cdot \:5-10-2\left(1-2\right)+5\)
\(\mathrm{Follow\:the\:PEMDAS\:order\:of\:operations}\)
\(=4\cdot \:5-10-2\left(-1\right)+5\)
\(=20-10-2\left(-1\right)+5\)
\(=20-10-\left(-2\right)+5\)
\(20-10=10\)
\(=10-\left(-2\right)+5\)
\(-\left(-2\right)=+2\)
\(=10+2+5\)
\(10+2=12\)
\(=12+5\)
\(12+5=17\)
\(=17\)
Solve w(raised to the 2nd power)=81, where w is a real number. Simplify your answer as much as possible.
w=?
Answers
Answer:
9
Step-by-step explanation:
9 to the second power would be 9 times 9, which equals 81
A bed has a sale price of £257.40
This is a saving of 22% on the original price.
What was the original price of the bed?
Answers
The original price of the bed was £330.
Calculating priceFrom the question, we are to determine the original price of the bed.
Let the original price of the bed be x
From the given information,
The current sale price of the bed is £257.40, and this price is a saving of 22% on the original price
Then,
We can write that
x - 22% of x = £257.40
Thus,
x - 0.22x = £257.40
0.78x = £257.40
x = £257.40/0.78
x = £330
Hence, the original price of the bed was £330.
Learn more on Calculating price here: https://brainly.com/question/7459025
#SPJ1
Answer:330
Step-by-step explanation:
easy way to do this:
1. ok so you know 100%=x and 100-22=73 so that means that 73%=2570.40
2. so write them with the known above the unknown: 100%=x
78%=2457.40
3. no cross multiply like this \(\frac{100X257.40}{78}\) imagine the multiplication sign is the X here( the app didn't let me change that?)
4. the solution equals 330 which the answer
5. YOU DID IT!!
Max wants to rent a bicycle. The cost to rent a bike is a $5 insurance fee plus $3 per hour. Max has at most $20 to spend. Write an inequality to represent this scenario. Give a value that satisfies the inequality.
Answers
Answer: 5 + 3x ≤ 20; 5
Step-by-step explanation:
at most means not more than(less or equal to),which use the symbol ≤. Let x be the hour that Max rent.
5 + 3x ≤ 20
3x ≤ 15 [Subtract 5 from both sides.]
x ≤ 5 [Divide 3 from both sides.]
Any value less than or equal to 5 will be satisfies the inequality.
10. Set up and evaluate the definite integral for the area of the surface generated by revolving the curve a) (3 pts.)y= 6x 3+ 2x1 ,1≤x≤2, about the x-axis; b) (3 pts.) x= 4y−1,1≤y≤4, about the y-axis.
Answers
The definite integral for the area of the surface generated by revolving the curve y = 6x^3 + 2x about the x-axis, over the interval 1 ≤ x ≤ 2, can be set up and evaluated as follows:
∫[1 to 2] 2πy √(1 + (dy/dx)^2) dx
To calculate dy/dx, we differentiate the given equation:
dy/dx = 18x^2 + 2
Substituting this back into the integral, we have:
∫[1 to 2] 2π(6x^3 + 2x) √(1 + (18x^2 + 2)^2) dx
Evaluating this definite integral will provide the surface area generated by revolving the curve about the x-axis.
b) The definite integral for the area of the surface generated by revolving the curve x = 4y - 1 about the y-axis, over the interval 1 ≤ y ≤ 4, can be set up and evaluated as follows:
∫[1 to 4] 2πx √(1 + (dx/dy)^2) dy
To calculate dx/dy, we differentiate the given equation:
dx/dy = 4
Substituting this back into the integral, we have:
∫[1 to 4] 2π(4y - 1) √(1 + 4^2) dy
Evaluating this definite integral will provide the surface area generated by revolving the curve about the y-axis.
By setting up and evaluating the definite integrals for the given curves, we can find the surface areas generated by revolving them about the respective axes. The integration process involves finding the appropriate differentials and applying the fundamental principles of calculus.
To know more about integral follow the link:
https://brainly.com/question/33191486
#SPJ11
The change in the value of a linear function f(x) as x increases is shown in the table below.
f(x) -3 -2 -1 0
x -2 0 2 4
What is the rate of change? Decimal form.
m=
Answers
Answer:
m = 1/2
Step-by-step explanation:
\(m = \frac{ - 2 - ( - 3)}{0 - ( -2)} = \frac{1}{2} \)
is 6:1 equivalent to 12:3
Answers
Answer: No, absolutely not,
Step-by-step explanation: 6x2 = 12, so you have to multiply by 2 on each side. 1x2=2, so the equivilent ratio is 12:2!
Answer: Nope
Step-by-step explanation: No, because you can see they multiply 1 x 3 to get to 3, but if you multiply 6 x 3, it equals 18, not 12. (6 x 2 = 12) but they have to have the same denominator and numerator to be equivalent. Therefore, no, they are not equivalent.
Bonnie bought 12 bottles of pineapple juice and apple juice. The bottles of pineapple juice, p, were on sale for $1 per bottle, and the bottles of apple juice, a, were on sale for $1.75 per bottle. Bonnie spent a total of $15. How many bottles of pineapple juice and apple juice did Bonnie buy?
Answers
Answer:
Step-by-step explanation:
Let's use a system of equations to solve the problem.
We know that Bonnie bought a total of 12 bottles, so:
p + a = 12
We also know that Bonnie spent a total of $15, so:
1p + 1.75a = 15
We can solve this system of equations by substitution or elimination. Here, we'll use substitution:
p = 12 - a (from the first equation)
1(12 - a) + 1.75a = 15 (substituting p in the second equation)
12 - a + 1.75a = 15
0.75a = 3
a = 4
So Bonnie bought 4 bottles of apple juice. We can find the number of bottles of pineapple juice by substituting a=4 into the first equation:
p + 4 = 12
p = 8
Therefore, Bonnie bought 8 bottles of pineapple juice and 4 bottles of apple juice.
Solve this problem with a proportion: The ratio
of busy beavers to chatty chipmunks is 11 to
12. If there are 48 chatty chipmunks, how
many busy beavers are there?
Answers
The number of busy beavers is found as 33.
Explain about the proportion of numbers?Mathematical proportions are comparisons of two numbers typically represent objects or persons. They are frequently expressed as fractions or with a colon.A mathematical comparison of two numbers is called a percentage.The given ratio:
busy beavers/ chatty chipmunks = 11/ 12
For, 48 chatty chipmunks
busy beavers/ 48 = 11/ 12
busy beavers/ 48 = 11/ 12
busy beavers = 11*3
busy beavers = 33
Thus, the number of busy beavers is found as 33.
To know more about the proportion, here
https://brainly.com/question/870035
#SPJ1
TEN POINTS!!!!!1 Find the y-intercepts for the parabola defined by this equation y=-6x^2 -7x-2
Answers
Answer:
y intercept: -2
x intercepts: -0.6667 and -0.5
Step-by-step explanation:
Check out this graph: Hope that this helped you!

Mary has borrowed 48 books from the library. This is 22% of all of the books in the library. How many books are in the library?
Answers
Answer:
218
Step-by-step explanation:
ATQ,
22%of total books = 48
Let the total no. of books in library be x.
22/100x=48
x=4800/22
X=218(approximately)
In exactly one year, how many mice would there be at school? EXPLAIN FULLY AND SHOW ALL WORK:Equation: Y=a(4)^xWhere:a is the initial value (when the generation = 0)x is the generation.
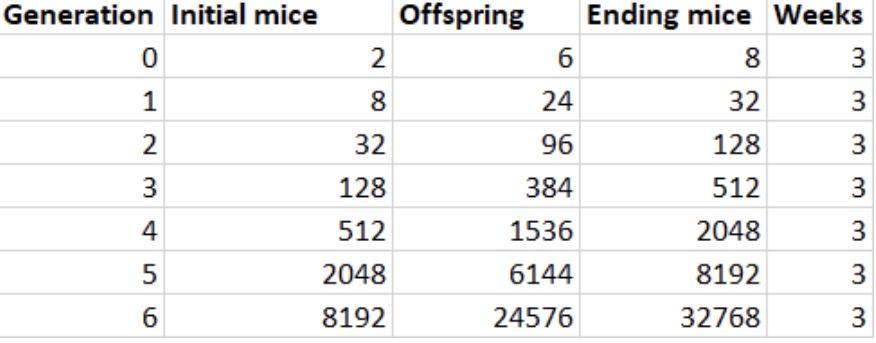


Answers
We know that each generation takes approximately 3 weeks, then, we can estimate how many generations we do have in one year, remember that one year has
\(1\text{ year }\approx52.14286\text{ weeks}\)Then, in one year we have
\(\frac{52.14286}{3}=17.383\text{ generations}\)In the real world, we can't have half of a generation or a decimal generation, then, let's approximate it to the nearest integer, in that case, 17 generations.
We have the expression that predicts the number of mice, then we can use that equation to find the result for 17 generations:
\(\begin{gathered} \text{ Initial Mice:} \\ f(x)=2\cdot4^x \end{gathered}\)Evaluate that at x = 17
\(\begin{gathered} \text{ Initial Mice} \\ f(x)=2\cdot4^x\Rightarrow f(17)=2\cdot4^{17}\Rightarrow3.44×10^{10} \end{gathered}\)With an offspring of
\(\begin{gathered} \text{ Offspring} \\ f(x)=6\cdot4^x\Rightarrow f(17)=6\cdot4^{17}=1.03×10^{11} \end{gathered}\)And the ending mice
\(\begin{gathered} \text{ Ending Mice} \\ f(x)=8\cdot4^x\Rightarrow f(17)=8\cdot4^{17}=1.37×10^{11} \end{gathered}\)Therefore, the final answer is
\(\text{ Ending mice = }1.37\times10^{11}\)h(t)= (t+3)^2 + 5
What is the average rate of change of h over the interval -5 < t < -1?
Answers
Answer:
The average rate of change for the given function in the interval (-5, -1) is 0 (zero)
Step-by-step explanation:
The average rate of change of a function over an interval is the quotient between the difference between the function evaluated at the ends of the interval divided by the length of the interval. That is for our case:
the average rte of change of h(t) in the interval (-5, -1) is:
\(\frac{h(-1)-h(-5)}{-1+5}\)
so we find:
\(h(-1)=(-1+3)^2+5=2^2+5=4+5=9\\and\\h(-5)=(-5+3)^2+5=(-2)^2+5=4+5=9\)
then the average rate of change becomes:
\(\frac{h(-1)-h(-5)}{-1+5}=\frac{9-9}{4} =\frac{0}{4} =0\)
Write the perimeter of the triangle in simplest form
can i please get help

Answers
patients scheduled to see their primary care physician at a particular hospital wait, on average, an additional ten minutes after their appointment is scheduled to start. assume the time that patients wait is exponentially distributed. what is the probability a randomly selected patient will see the doctor within fourteen minutes of the scheduled time?
Answers
Therefore , the solution of the given problem of probability comes out to be 59.3% chance that an arbitrarily chosen patient will see the doctor within 14 minutes of the appointment time.
What precisely is probability?The determination of the likelihood that an assertion is accurate or that a particular event will occur is the main objective of the systems within the process known as criteria. Chance can be represented by any number between 0 and 1, where 0 is frequently used to indicate that it's possible and 1 is frequently used to signify a degree of confidence. A probability diagram shows the likelihood that a particular occurrence will occur.
Here,
With a mean of 10 minutes and an exponential distribution, X has the following probability density function:
=> For x >= 0, f(x) = (1/10) * e(-x/10).
The likelihood that an arbitrarily chosen patient will see the doctor within 14 minutes of the appointment time is what we are trying to determine. This can be stated as follows:
=> P(X <= 14)
Integrate the density function from 0 to 14 to discover this probability:
=> P(X = 14) = e(-x/10) * [0,14] (1/10)
=> P(X = 14) = 0 1.4 e (-u) du
The integral's evaluation yields:
=> P(X <= 14) = [\(-e^{-u}\)] between 0 and 1.4
=> P(X <= 14) = -e⁻¹⁴ + 1
=> P(X <= 14) ≈ 0.593
This means that there is a 59.3% chance that an arbitrarily chosen patient will see the doctor within 14 minutes of the appointment time.
To know more about probability visit:
https://brainly.com/question/11234923
#SPJ1
Which quadratic equation?

Answers
Answer:
step 1. plug in (-3, 0).
step 2. y = x^2 + x - 6 works and the others dont.
step 3. plug in (-2, -4), (-1, -6), (0, -6), (1, -4), (2, 0)
step 4. All points work in the equation x^2 + x - 6.
are percentage like ratios or fractions
Answers
Answer:
ratios
Step-by-step explanation:
what is the predicted value and the 95% confidence interval of the rear width of a female crab whose carapace width is 36.4 mm and whose species is orange?
Answers
Based on statistical analysis, the predicted value of the rear width of a female orange crab with a carapace width of 36.4 mm is approximately 25.8 mm. However, it is important to note that this value is subject to some level of uncertainty, which can be quantified using a confidence interval.
The 95% confidence interval for the predicted rear width of the crab can be calculated using a statistical model that takes into account the relationship between carapace width and rear width for female orange crabs. This interval can be calculated as follows:
Lower limit = predicted value - (1.96 x standard error)
Upper limit = predicted value + (1.96 x standard error)
Assuming that the standard error is 2.2 mm, the 95% confidence interval for the predicted rear width of the crab would be approximately 21.4 mm to 30.2 mm.
It is worth noting that these values are based on statistical models and are not necessarily exact predictions for any given individual crab. Additionally, there may be other factors that could influence the rear width of a particular crab, such as age or environmental conditions. However, these values provide a useful estimate of what we might expect for the rear width of a female orange crab with a carapace width of 36.4 mm.
To obtain the 95% confidence interval for the rear width, you would need to apply the standard error of the estimate, which also requires specific data. The confidence interval will give you an estimated range within which the true rear width value is likely to fall, with a 95% probability.
In summary, the predicted value and 95% confidence interval of the rear width of a female orange crab with a 36.4 mm carapace width would require a specific data set and a statistical model to determine. Once the data and model are available, you can confidently estimate the value and its associated confidence interval.
Learn more about crab at : brainly.com/question/3413741
#SPJ11
A hemispherical tank is filled with water and has a diameter of 12 feet. If water weighs 62.4 pounds per cubic foot, what is the total weight of the water in a full tank, to the nearest pound?
Answers
Answer:
The total weight = 1286 × 62.4 = 80246 pounds.
Step-by-step explanation:
The formula of the volume of the sphere is
V = 4/3×π×r³
Given
d = 17 feet
d = 2r
r = d/2 = 17/2 = 8.5 feet
V = 4/3×π×r³
Since we need half of the volume as it is a hemispherical tank.
= 1286 ft³
Given that the weighs 62.4 pounds per cubic foot
Thus, the total weight = 1286 × 62.4 = 80246 pounds.

does 8b−10+b+3b+2=7+2b+10b−18−3 have a solution
Answers
Answer:
No.
Step-by-step explanation:
If we combine all like terms first on the left, then the right-
We will have a solution of
-8+12b=12b-14
This is not true, therefore, 8b−10+b+3b+2=7+2b+10b−18−3 does not have a solution.
(DM or comment for further explanation)
Which number is greater? Also please explain because I'm gonna have a test on this on Friday and I'm still kinda confused.

Answers
Polina has some juice pouches that each contain 7 fluid ounces of juice. write an equation that relates the number of juice pouches (p) to the total volume of juice (j) in fluid ounces
Answers
Each of Polina's juice pouches holds 7 fluid ounces of juice. A equation that connects the quantity of juice in each pouch to the overall amount in fluid ounces is p-7j=0.
Given that,
Each of Polina's juice pouches holds 7 fluid ounces of juice.
We have to create a equation that connects the quantity of juice in each pouch (p) to the overall amount (j) in fluid ounces.
The equation is p=7j
p-7j=0
Therefore, a equation that connects the quantity of juice in each pouch (p) to the overall amount (j) in fluid ounces is p-7j=0.
To learn more about equation visit: https://brainly.com/question/10413253
#SPJ1
Solve and sketch its graph
1. 3x^2 - 4x = 0
Answers
Step-by-step explanation:
By solving, I am assuming that you want to find the zeros.
So to find what x equals, first, you factor out an x.
3x² - 4x = 0
x(3x - 4) = 0
Here, you can separate the equation into two different equations to solve for x.
3x - 4 = 0 and x = 03x = 4x = \(\frac{4}{3}\) and x = 0Those are your zeros.
And for its graph, you can always look to an online graphing calculator. I used Desmos.

Based on these data, estimate the number of days that the dow decreased by more than 1% in these 61 days.
Answers
Number of the 61 days in 2009 the Dow decreased by more than 1% is 0.514.
What is normal distribution?A probability distribution that is symmetric about the mean is the normal distribution, sometimes referred to as the Gaussian distribution. It demonstrates that data that are close to the mean occur more frequently than data that are far from the mean.
Given:
61 days in 2009 the Dow decreased by more than 1%.
In 2009
z = (1- (-0.198))/2.331
z = 0.514
In 2010
z = (1-0.078)/0.821
z = 1.123
Thus, number of the 61 days in 2009 the Dow decreased by more than 1% is 0.514.
learn more about normal distribution here:
brainly.com/question/14916937.
#SPJ1
What is the value of x in the image below?

Answers
Answer:
a
Step-by-step explanation:
(14) (55, 42, 32, 48, 55, x), mean = 49
Answers
Answer:
78
Step-by-step explanation:
Add all the numbers given =256 then take the mean and multiply it with 7 =334 then take 334_256=78 and done
Find the angle between vector bold lower u equals 3 bold lower I plus start root 3 end root bold lower j and vector bold lower v equals negative 2 bold lower I minus 5 bold lower j to the nearest degree. A. 82° B. 38° C. 142° D. 98°
Answers
Answer:
C. 142°
Step-by-step explanation:
You want the angle between vectors u=3i+√3j and v=-2i-5j.
AngleThere are a number of ways the angle between the vectors can be found. For example, the dot-product relation can give you the cosine of the angle:
u•v = |u|·|v|·cos(θ) . . . . . . where θ is the angle of interest
You can find the angles of the vectors individually, and subtract those:
u = |u|∠α
v = |v|∠β
θ = α - β
When the vectors are expressed as complex numbers, the angle between them is the angle of their quotient:
\(\dfrac{\vec{u}}{\vec{v}}=\dfrac{|\vec{u}|\angle\alpha}{|\vec{v}|\angle\beta}=\dfrac{|\vec{u}|}{|\vec{v}|}\angle(\alpha-\beta)=\dfrac{|\vec{u}|}{|\vec{v}|}\angle\theta\)
This method is used in the calculation shown in the first attachment. The angle between u and v is about 142°.
A graphing program can draw the vectors and measure the angle between them. This is shown in the second attachment.
__
Additional comment
The approach using the quotient of the vectors written as complex numbers is simply computed using a calculator with appropriate complex number functions. There doesn't seem to be any 3D equivalent.
The dot-product relation will work with 3D vectors as well as 2D vectors.
<95141404393>


1) Working alone, Ryan can dig a 10 ft by 10 ft
hole in five hours. Castel can dig the same
hole in six hours. How long would it take
them if they worked together?
Answers
Step-by-step explanation:
(Ryan+ castel)/2
(5+6)/2
11/2
5.5 hrs or 5½ hrs
Let X be a random variable that takes values in the set SX = {0, 1, 2}. Find a probability mass
function (PMF) for X under which E[X] = 1/2 and E(X2) = 4/5 .
Answers
The probability mass function (PMF) for X is:P(X = 0) = 13/20,P(X = 1) = 1/5,P(X = 2) = 3/20
To find a probability mass function (PMF) for the random variable X that satisfies the given expectations, we can define the probabilities for each value of X and solve for them.
Let's denote the probability of X taking the value x as P(X = x). According to the problem, we have the following expectations:
E[X] = 1/2
E(X^2) = 4/5
The expectation of X is given by:
E[X] = Σ(x * P(X = x))
For X = 0, we have:
0 * P(X = 0) + 1 * P(X = 1) + 2 * P(X = 2) = 1/2
This equation can be rewritten as:
P(X = 1) + 2 * P(X = 2) = 1/2
Similarly, the expectation of X^2 is given by:
E(X^2) = Σ(x^2 * P(X = x))
For X = 0, we have:
0^2 * P(X = 0) + 1^2 * P(X = 1) + 2^2 * P(X = 2) = 4/5
Simplifying, we get:
P(X = 1) + 4 * P(X = 2) = 4/5
We now have a system of two equations with two unknowns:
P(X = 1) + 2 * P(X = 2) = 1/2
P(X = 1) + 4 * P(X = 2) = 4/5
Solving this system of equations, we can find the values of P(X = 1) and P(X = 2).
Multiplying the first equation by 2, we get:
2 * P(X = 1) + 4 * P(X = 2) = 1
Subtracting the second equation from this, we have:
(2 * P(X = 1) + 4 * P(X = 2)) - (P(X = 1) + 4 * P(X = 2)) = 1 - 4/5
P(X = 1) = 1 - 4/5
P(X = 1) = 1/5
Substituting this back into the first equation, we find:
1/5 + 2 * P(X = 2) = 1/2
2 * P(X = 2) = 1/2 - 1/5
2 * P(X = 2) = 5/10 - 2/10
2 * P(X = 2) = 3/10
P(X = 2) = (3/10) / 2
P(X = 2) = 3/20
Finally, since the probabilities must sum to 1, we have:
P(X = 0) = 1 - P(X = 1) - P(X = 2)
P(X = 0) = 1 - 1/5 - 3/20
P(X = 0) = 20/20 - 4/20 - 3/20
P(X = 0) = 13/20
Therefore, the probability mass function (PMF) for X is:
P(X = 0) = 13/20
P(X = 1) = 1/5
P(X = 2) = 3/20
Learn more about probability here:
https://brainly.com/question/25870256
#SPJ11