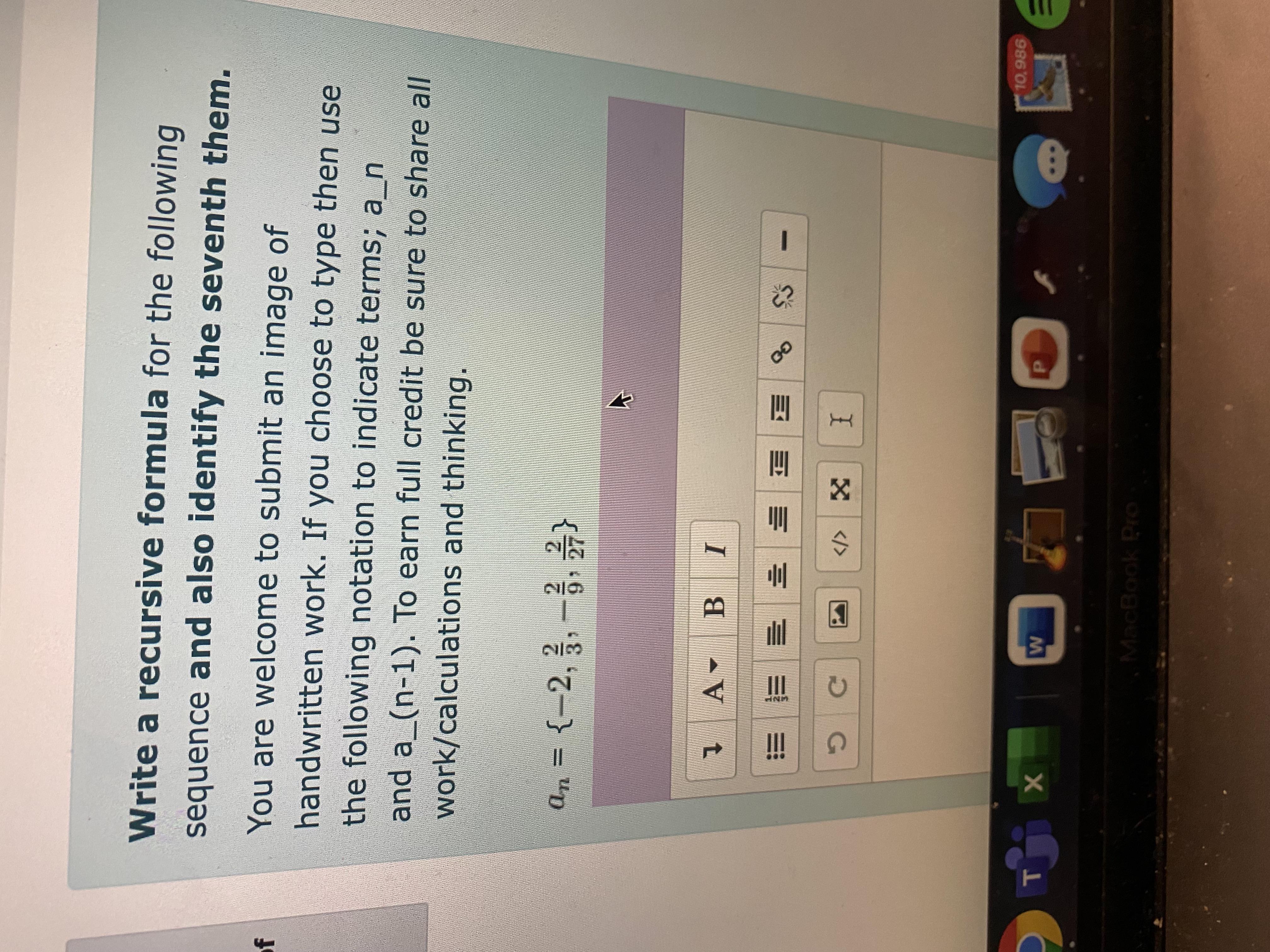
Write a recursive formula for the following sequence and also identify the seventh them. You are welcome to submit an image of handwritten work. If you choose to type then use the following notation to indicate terms; a_n and a_(n-1). To earn full credit be sure to share all work/calculations and thinking.a_n = {-2, \frac{2}{3}, -\frac{2}{9}, \frac{2}{27}}
Answers
EXPLANATION:
We are given a sequence and the first and second terms are;
\(\begin{gathered} a_1=-2 \\ a_2=\frac{2}{3} \end{gathered}\)The common ratio is determined by dividing a term by its preceeding term. Hence, we can derive the common ratio by dividing the second term by the first.
\(\begin{gathered} Common\text{ }ratio: \\ r=\frac{2}{3}\div\frac{-2}{1} \end{gathered}\)\(r=\frac{2}{3}\times\frac{1}{-2}\)\(r=-\frac{1}{3}\)The recursive formula for this sequence would be given as follows;
\(a_n=a_{n-1}\times r\)Where the variables are;
\(\begin{gathered} a_n=nth\text{ term} \\ r=-\frac{1}{3} \end{gathered}\)We now have;
\(a_n=a_{n-1}(-\frac{1}{3})\)For the 5th term we would have;
\(a_5=a_4(-\frac{1}{3})\)\(a_5=\frac{2}{27}(-\frac{1}{3})\)\(a_5=-\frac{2}{81}\)For the 6th term we would have;
\(a_6=a_5(-\frac{1}{3})\)\(a_6=-\frac{2}{81}\times(-\frac{1}{3})\)\(a_6=\frac{2}{243}\)For the 7th term we would have;
\(a_7=a_6(-\frac{1}{3})\)\(a_7=\frac{2}{243}(-\frac{1}{3})\)\(a_7=-\frac{2}{729}\)ANSWER:
\(\begin{gathered} Recursive\text{ }formula: \\ a_n=a_{n-1}(-\frac{1}{3}) \\ 7th\text{ }term: \\ a_7=-\frac{2}{729} \end{gathered}\)Related Questions
just explain how this is "Reflexive Property" (30 points)!!
Answers
The Reflexive Property is a property of equality that states that anything is equal to itself. This property is true for numbers, shapes, angles, and more.
In the context of geometry, the Reflexive Property of Congruence states that any geometric figure is congruent to itself. This includes angles, segments, triangles, and other polygons.
So, when you see "<J ≅ <J", it's saying that angle J is congruent to angle J, which is an application of the Reflexive Property. In other words, any angle is congruent (equal in measure) to itself.
FIND THE AREA I WILL MARK BRAINLIEST
Answers
Answer:
Hello! answer: 104
Step-by-step explanation:
(base × height)
13 × 8 = 104 therefore the area is 104 hope that helps!
Answer:
104
Step-by-step explanation:
8*13
A model car is 7.5 inches long made with a scale of 2 inches = 48 inches. How long is the actual car?
A. 15 ft
B. 20 ft
C. 180 ft
D.360 ft
Answers
Answer:
360
Step-by-step explanation:
reduce 5/10 to it's smallest fraction
Answers
Answer:
1/2
If you divide both numbers by 5, you would get 1/2
Both the numerator and the denominator have the greatest common factor of 5. You can divided both the top and bottom by 5, giving you 1/2.
Which is the equation of the given line in point-slope form?
y−0=−1(x−8)
y−0=1(x+8)
y=−x+8
y−8=−1(x+0)
Answers
Answer:
y = -x + 8
Step-by-step explanation:
Let's break down the equation step by step to understand it better.
The equation in point-slope form is given as:
y - y1 = m(x - x1)
In this case, we have:
y - 0 = -1(x - 8)
The point-slope form uses a specific point (x1, y1) on the line and the slope (m) of the line.
Here, the point (x1, y1) is (8, 0), which represents a point on the line. This means that when x = 8, y = 0. The graph has a point at (8, 0), which confirms this information.
The slope (m) is -1 in this equation. The slope represents the rate at which y changes with respect to x. In this case, since the slope is -1, it means that for every unit increase in x, y decreases by 1. The negative sign indicates that the line has a downward slope.
By substituting the values into the equation, we get:
y - 0 = -1(x - 8)
Simplifying further:
y = -x + 8
This is the final equation of the line in slope-intercept form. It tells us that y is equal to -x plus 8. In other words, the line decreases by 1 unit in the y-direction for every 1 unit increase in the x-direction, and it intersects the y-axis at the point (0, 8).
If the graph has points at (0, 8) and (8, 0), the equation y = -x + 8 accurately represents that line.
PLEASE ANSWER ASAP FOR BRAINLEST!!!!!!!!!!!!!!!! ALL LINKS WILL BE REPORTED!!!!!!!!!!!!!!!
Answers
Answer:
i thiiiink its b
Step-by-step explanation:
1. What is the next term of the arithmetic sequence 6, 10, 14, 18
Answers
Write an equation in point-slope form of the line that passes through the given point and has the given slope. (2, 7); m = -4
Answers
Answer:
y-7=-4(x-2)
Step-by-step explanation:
y-y1=m(x-x1)
y-7=-4(x-2)
The FDA is testing a new ointment designed to deliver 3.5 micrograms of active ingredient to each square centimeter of skin. Nine(9) subjects apply the ointment and then six hours later that amount of drug absorbed by the skin is measured. To determine if there is enough evidence that the mean amount of drug absorbed is different from 3.5 micrograms at the α=0.01 significance level, we would need to compare our test statistic to what critical
Answers
Answer:
t(c) = 3.355
Step-by-step explanation:
We assume a normal distribution, and with sample size n = 9 we should follow a t -student test on both tails since the FDA is interested in determining if the amount of drug absorbed is different from 3.5 micrograms.
Therefore if α = 0,01 that means that confidence interval is 99 % or 0,99
Finally with α/2 = 0,005 and 8 degrees of freedom we find in t-student table t(c) = 3.355
2 column proof please help
Answers
Answer: Definition of bisector
Step-by-step explanation: It bisects it so its Def. Of Bisector.
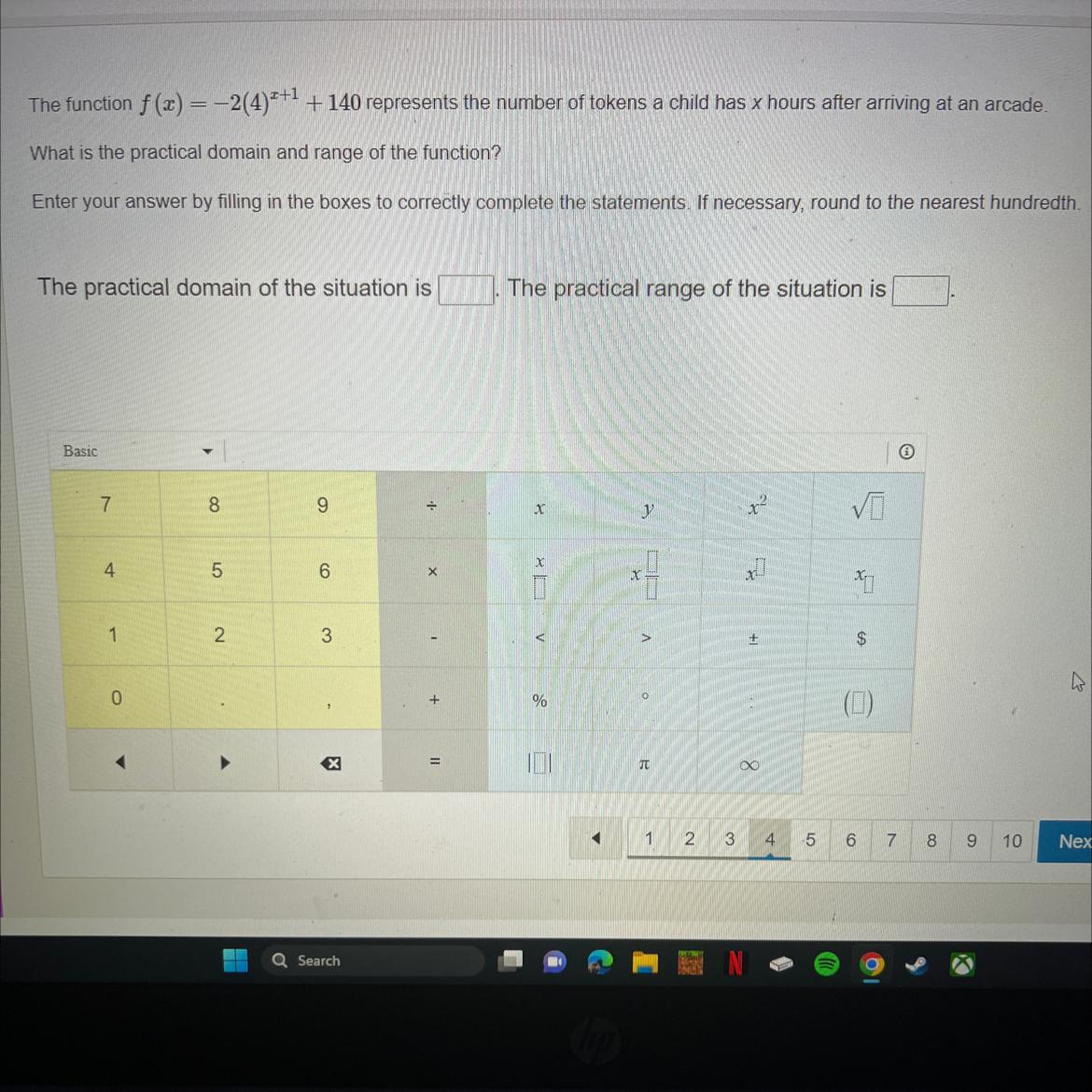
The function f(x) = -2(4)²+1 +140 represents the number of tokens a child has x hours after arriving at an arcade.
What is the practical domain and range of the function?
Enter your answer by filling in the boxes to correctly complete the statements. If necessary, round to the nearest hundredth.
The practical domain of the situation is ?
The practical range of the situation is ?
Answers
The practical domain of the situation is all real numbers, since there is no restriction on the number of hours the child can spend at the arcade.
The practical range of the situation is [1,140], since the minimum value of the function is 1 and the maximum value is 140.
HELP!!!!!! Which point approximates V3?
A) A
B) B
C C
D D
Answers
Answer:
c
ssusjs8snwi3heene8je
simplest form of -1/2 + 4/9
Answers
Answer:
1/18
-1/2 = 9/18
4/9 = 8/18
-8/18+9/18 = 1/18
7. The mean age at first marriage for respondents in a survey is 23.33,
with a standard deviation of 6.13. For an age at first marriage of 33.44,
the proportion of area beyond the Z score associated with this age is
.05. What is the percentile rank for this score?
Answers
Answer:
\( \mu = 23.33, \sigma =6.13\)
And for this case we are analyzing the value os 33.44 and we can use the z score formula given by:
\( z=\frac{X -\mu}{\sigma}\)
And replacing we got:
\( z=\frac{33.44 -23.33}{6.13}= 1.649\)
We know that the proportion of area beyond the Z score associated with this age is .05 so then the percentile would be: 95
Step-by-step explanation:
For this case we have the following parameters:
\( \mu = 23.33, \sigma =6.13\)
And for this case we are analyzing the value os 33.44 and we can use the z score formula given by:
\( z=\frac{X -\mu}{\sigma}\)
And replacing we got:
\( z=\frac{33.44 -23.33}{6.13}= 1.649\)
We know that the proportion of area beyond the Z score associated with this age is .05 so then the percentile would be: 95
A large flagpole stands outside of an office building. Marquis realizes that when he looks up from the ground, 60m away from the flagpole, and the top of the building line up. If the flagpole is 35m tall, and Marquis is 170m from the building, how tall is the building?
Answers
Answer:
99.166666666666666666666; 595/6; 99 1/6; 99
Step-by-step explanation:
THE FORMULA IS (x)/(170)=(35)/(60)
solve for x
copy the formula in bold and paste it to math w]y:
(x)/(170)=(35)/(60)
choose the option to solve for x and 99.666666666666∞ is the answer.
Solve for z in the system of equations.
x + y - z = -5
2x - y + z = 8
x - 4y + 3z = 5
Answers
Answer:
z = 20
Step-by-step explanation:
Elimination Method:We can use the elimination method in a systems of 3 equations, just as we did when we were solving systems of 2 equations. While the method we apply it is the same, we have to apply it multiple times as elimination gets rid of one variable (usually) and since we're dealing with 3 variables, that still leaves us with 2 variables and we need to cancel once more.
Applying Elimination Method:
We want to develop two linear equations, by applying elimination twice to each equation at least once, and then from there we can apply elimination once more.
Since we're solving for "z", we don't want to immediately cancel it out. So let's use the following two equations:
\(x+y-z=-5\\\\x-4y+3z\)
Let's cancel out the "x", by manipulating one equation to be -x. We can do this by multiplying one equation by -1, but remember we have to apply this to both sides of the equation. Let's do it to the top one (you could also do it to the bottom one)
\(-1(x+y-z)=-(-5)\implies -x-y+z=5\)
So now let's add the two equations:
\(\ \ \ (-x-\ y+\ z)=5\\+(\ \ x-4y + 3z) = 5\\ ------------\\ -5y+4z=10\)
Now let's apply the same thing, but to the middle and bottom equation. Since they don't have the same absolute value coefficients (ignoring the sign) we need to multiple one by a value other than just negative one. So let's multiply the bottom equation by -2 so that the bottom will have a -2x which will cancel when adding it to 2x
\(-2(x - 4y + 3z) = -2(5)\\-2x + 8y - 6z = -10\)
Now let's add the equations:
\(\ \ \ (\ \ 2x-y+z)=8\\+(-2x + 8y - 6z)=-10\\\\-----------\\7y - 5z = -2\)
So now we have the two equations:
\(7y-5z=-2\\-5y+4z=10\)
From here we can apply any method we want, from here I'll use substitution. Since we want to get rid of the "y", let's solve for "y" in terms of z, so once we substitute we have no "y" terms left.
\(7y-5z=-2\\7y=5z-2\\y=\frac{5z-2}{7}\)
Now let's plug this into the second two-variable equation we made.
\(-5(\frac{5x-2}{7})+4z=10\\\\\frac{-25x+10}{7}+4z=10\\\\\frac{-25}{7}z+\frac{10}{7} + \frac{28}{7}z = \frac{70}{7}\\\\\frac{-25+28}{7}z = \frac{70-10}{7}\\\\\frac{3}{7}z = \frac{60}{7}\\\\z = \frac{60}{7} * \frac{7}{3}\\\\z = 20\)
You are ready to buy a house, and you have $31,000 for a down payment and closing costs. Closing costs are estimated to be 4% of the loan value. You have an annual salary of $36,000, and the bank is willing to allow your monthly mortgage payment to be equal to 28% of your monthly income. The interest rate on the loan is 6% per year with monthly compounding (0.5% per month) for a 30-year fixed rate loan. How much money will the bank loan you?
Answers
Answer:
$ 140,104.96
Step-by-step explanation:
The amount the bank will the individual is the present value of the total mortgage payment.
monthly mortgage payment=28%*$36,000/12=$840
the payment is meant for 30 years but 360 months i.e 12*30
the amount of loan is the present value of $840 monthly for 360 months with 0.5% interest rate per month
=pv(rate,nper,-pmt,fv)
rate is 0.5%
nper is 360 months
pmt is $840 per month
fv is the total payments which is unknown
=pv(0.5%,360,-840,0)=$140,104.96
The loan amount is closest to $ 140,104.96
What is the formula to find the area of a circle?
Answers
Answer:
A= \(\pi\)r²
Step-by-step explanation:
the area of a circle
If AB is 126, what does x equal? HELPPP
Answers
Reason
126/2= 63
9x+18=63
9x=45
x=5
(X-2)^2 - (x-4)^2 simplify
Answers
which diagram below appears to show a pair of perpendicular lines Diagram A Diagram B Diagram C. Explain your Answer.
Answers
The answer for it is diagram B because it does not cross or have parallel lines
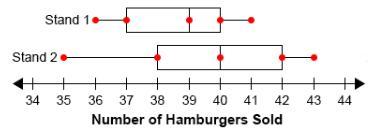
Two competing concession stands recorded the number of hamburgers sold daily for one week.
Which statement correctly compares the data?
A. The number of hamburgers sold daily at stand 1 is generally less than that sold at stand 2.
B. The number of hamburgers sold daily at both stands is approximately the same.
C. The number of hamburgers sold daily at stand 2 is generally less than that sold at stand 1.
D. Although the median number of hamburgers sold daily at stand 1 is generally less than that at stand 2, the variability creates too much overlap for any conclusion to be made.
Answers
We can respond to that by addressing the problem at hand equation Option D claims that even though stand 1 typically sells fewer hamburgers on average per day than the median quantity,
What is equation?A math equation is a procedure that connects two claims and uses the equals symbol (=) to denote equivalence. An equation in algebra is a mathematical statement that establishes the equivalence of two mathematical expressions
According to Option A, fewer hamburgers are typically served each day at Stand 1 than at Stand 2. If the evidence are consistent with this assertion, it would be true.
Option B claims that both stands sell roughly the same amount of hamburgers every day. If the statistics for both stands are remarkably comparable and the discrepancy between them is not great, then this would be the accurate statement.
Option C claims that, on average, fewer hamburgers are sold each day at stand 2 than at stand 1. If the evidence are consistent with this assertion, it would be true.
Option D claims that even though stand 1 typically sells fewer hamburgers on average per day than the median quantity,
To know more about equation visit:
https://brainly.com/question/649785
#SPJ1
Malcolm has $50 gift card to a local car wash and order is the ultimate car wash each visit is $8.95
Answers
The amount cheaper is the car washes Malcolm orders than the car washes Martha's order is $13.
The correct answer choice is option B.
How much cheaper is the car washes Malcolm orders than the car washes Martha's order?Malcolm's gift card = $50.
Cost Malcolm's car wash per visit = $7
Martha's gift card = $180
Cost Martha's car wash per visit = Difference between gift card balance of first and second visit
= $180 - $160
= $20
How cheap is the car washes Malcolm orders than the car washes Martha's order = $20 - $7
= $13
Therefore, Malcolm's car wash is cheaper than Martha's car wash by $13
The complete question is attached in the diagram.
Read more on graphs:
https://brainly.com/question/19040584
#SPJ1
Find set A′ ∩ B′
U={a, b, c, d, e, f, g}
A={b, c, e, g}
Answers
Answer:
i dont know
Step-by-step explanation:
i dont know
Find the area of the polygon. Leave
your answer in exact form with proper units.
Answers
Answer:
15 square meters.
Hope this helped!
Write the numbers associated with the points that are
graphed on the complex plane.
Z1 =. + Oi
Z2 = 0 - I
Z3 =. +i
Answers
The complex numbers graphed on the plane are given as follows:
z1 = 3 + 0i.z2 = 0 - 2i.z3 = -2 + i.What are complex numbers?Complex numbers are number that are divided into a real part and an imaginary part, according to the definition given as follows:
z = a + bi.
In which:
a is the real part.b is the imaginary part.On the complex plane, we have that:
The horizontal axis represents the real part of the number.The vertical axis represents the imaginary prat of the number.As the number z1 has a horizontal coordinate of 3 and a vertical coordinate of 0, it is given as follows:
z1 = 3 + 0i.
As the number z2 has a horizontal coordinate of 0 and a vertical coordinate of -2, it is given as follows:
z2 = 0 - 2i.
As the number z3 has a horizontal coordinate of -2 and a vertical coordinate of 1, it is given as follows:
z3 = -2 + i.
More can be learned about complex numbers at https://brainly.com/question/10662770
#SPJ1
1. Show using the preimage theorem that the tangent space to the Stiefel manifold of orthonormal 2 -frames inRnat a point[v1,v2], is the vector space of vectors(u,w)∈Rn×Rnsatisfyingv1⋅uv2⋅wv1⋅w+v2⋅u=0=0=0.
Answers
As a result, the set of all [u, w] Rn Rn satisfying the previous equation is the tangent space to F at [v1, v2] by using preimage theorem.
Let F be the Stiefel manifold of orthonormal 2-frames in Rn to apply the preimage theorem. The collection of all tangent vectors to curves passing through [v1, v2] in F is what is known as the tangent space T[F] at a location [v1, v2]. Let (t) be a straight line in F such that (v1, v2) is a smooth curve. The tangent vector to t at time t = 0 is then given by
γ′(0) = [u, w] ∈ T[F].
We must now determine the requirements that [u, w] must meet in order to be in T[F]. Assume that V is a matrix with columns named v1 and v2. If Q is an orthogonal matrix, then any orthonormal 2-frame [v1′, v2′] in Rn can be represented as VQ. The category to which [v1′, v2′] belong Q is a 2 by 2 matrix with determinant 1, and F is equivalent to Q. Given that Q(0) = I, let Q(t) be a smooth curve in SO(2). Then, there is
γ(t) = VQ(t) (t),
and
γ′(0) = VQ′(0) (0).
We have Q since Q(t) is orthogonal (t)
TQ(t) = I, indicating
Q′(0)T + Q′(0) = 0.
Let [u, w] T[F] now. Once this is the case, a smooth curve Q(t) in SO(2) exists with Q(0) = I and
[u, w] = VQ′(0) (0).
Applying the equation above, we obtain
v1uv2w plus v1wv2u equals 0.
As a result, the set of all [u, w] Rn Rn satisfying the previous equation is the tangent space to F at [v1, v2].
to know more about" theorem" at https://brainly.com/question/343682
#SPJ4
Can someone help with this?
Answers
The value of f(x) . g(x) is 3x² + 5x - 2 two linear functions multiplied together to form a quadratic function.
What is a composite function?When the output of one function is given to the input of another function they are called composite functions.In (fog)x which is [f{g(x)}] here the out of the function g(x) is the input of the function f(x).
Given, Are two function f(x) 3x - 1 and g(x) = x + 2.
Now, f(x) . g(x) is nothing but multiplication of f(x) and g(x).
Therefore,
f(x) . g(x) = (3x - 1)(x + 2).
f(x) . g(x) = 3x² + 6x - x - 2.
f(x) . g(x) = 3x² + 5x - 2.
learn more about composite functions here :
https://brainly.com/question/5614233
#SPJ1
a summer soccer cam ordered a total of 84 soccer balls and t-shirts for the season. Soccer balls cost $25 each and t-shirts cost $9.50 each. if they paid $1,046 total for the purchase, how many of each item was ordered?
Answers
The Number of Soccer Balls is 16 and the Number of T-Shirts is 68
What is Linear Equation in Two Variables?
A linear equation in two variables is one that is stated in the form ax + by + c = 0, where a, b, and c are real integers and the coefficients of x and y, i.e. a and b, are not equal to zero.
Solution:
Let,
Number of Soccer Balls = x
Number of T-Shirts = y
Equation 1:
x + y = 84 -----------(i)
Equation 2:
25x + 9.5y = 1046 ----------(ii)
Multiplying Equation 1 by 25
25x + 25y = 2100 ---------(iii)
Substracting Equation2 from Equation 1
15.5y = 1054
y = 68
So, x = 16
To learn more about Linear Equation in Two Variables from the given link
https://brainly.com/question/24085666
#SPJ1
In 2014, the number of full-time students at your local community college was 1750. The admissions office anticipates that the enrollment will increase at a constant
rate of 130 students per year for the next several years
Answers
Answer:
\(y = 130x + 1750\)
Step-by-step explanation:
Given
\(a = 1750\) --- students in 2014
\(m = 130\) --- rate
Required
Write a linear equation for the scenario
A linear equation is represented as:
\(y =mx + a\)
Where
\(m \to\) rate
\(a \to\) y intercept i.e. initial value
So, we have:
\(y =mx + a\)
\(y = 130x + 1750\)
The linear equation y = 130x + 1750 with an increasing slope of 130 and a constant of 1750
What is the linear system?A Linear system is a system in which the degree of the variable in the equation is one. It may contain one, two, or more than two variables.
In 2014, the number of full-time students at your local community college was 1750.
The admissions office anticipates that the enrollment will increase at a constant rate of 130 students per year for the next several years.
We know that the equation of a line is given as
\(\rm y = mx + c\)
where m is the rate, c be the number of students in 2014.
Then we have
m = 130
c = 1750
Then the equation will be
\(\rm y = 130x + 1750\)
More about the linear system link is given below.
https://brainly.com/question/20379472