Write a recursive formula for an, the nth term of the sequence 12, 3, -6, ....
Answers
Answer:
tn= a+(n-1)d is formula
Related Questions
Work out the size of angle x

Answers
Answer:
as the sum of 2 opposite interior angles is equal to the sum of the exterior angle.
So here, X is the exterior angle.
and the measure of 2 opposite interior angles are 82° and 29°
Answer:
hope it helps.stay safe healthy and happy.
Line l passes through the points (−2,−1) and (2,−9), while line m passes through (0, 4) and (5,−6). Which statement best describes the relationship between lines l and m?
a. l and m are intersecting.
b. l and m are parallel.
c. l and m are collinear.
d. l and m are perpendicular.
Answers
Answer:
b. l and m are parallel.
Step-by-step explanation:
We need to figure out the equations of the two lines.
l passed through (-2, -1) and (2, -9)
y=-2x-5
m passed through (0, 4) and (5, -6)
y=-2x+4
The slope is the same, so the two lines are parallel.
Suppose that x represents one of two positive numbers whose sum is 28. Determine a function f(x) that represents the product of these two numbers.
Answers
The function that would give the product of the numbers is f(x) = x (28 - x)
What is a function in mathematics?A function in mathematics is a relationship between a set of inputs (referred to as the domain) and a set of outputs (referred to as the codomain or range), where each input is connected to each output exactly once. Each input value is given a distinct output value.
We are told that the sum of the two numbers is 28 thus;
Let the first number be x
'Let the second number be 28 - x
We would have that;
f(x) = x (28 - x)
Learn more about function:https://brainly.com/question/30721594
#SPJ4
Which is greater?-2 or +3,Which is greater +5 or -8,Which is greater -3 or 0,Which is greater -3 or +3
Answers
Answer:
+3 +5 0 +3
Step-by-step explanation:
negatives are always less then 0 and above
Answer:
1. 3
2. 5
3. 0
4. 3
Step-by-step explanation:
Write these numbers in order of size.
Start with the smallest number.
52 102 25 120 55
Answers
Answer:
YOUR ANSWER IS -
25,52,55,102 AND 120
You are trying to decide how much to save for retirement. Assume you plan to save $4,500 per year with the first investment made one year from now. You think you can earn 5.5% per year on your investments and you plan to retire in 35 years, immediately after making your last $4,500 investment. a. How much will you have in your retirement account on the day you retire? b. If, instead of investing $4,500 per year, you wanted to make one lump-sum investment today for your retirement that will result in the same retirement saving, how much would that lump sum need to be? c. If you hope to live for 17 years in retirement, how much can you withdraw every year in retirement (starting one year after rement will just exhaust your savings with the 17th withdrawal (assume your savings will continue to earn 5.5% in retirement)? d. If, instead, you decide to withdraw $90,000 per year in retirement (again with the first withdrawal one year after retiring), how many years will it take until you exhaust your savings? (Use trial-and-error, a financial calculator: solve for "N", or Excel: function NPER) e. Assuming the most you can afford to save is $900 per year, but you want to retire with $1,000,000 in your investment account, how high of a return do you need to earn on your investments? (Use trial-and-error, a financial calculator: solve for the interest rate, or Excel: function RATE)
Answers
This retirement planning scenario involves saving a fixed amount per year, earning a specified interest rate, and determining the final retirement account balance, lump-sum investment amount, annual withdrawal in retirement, and required interest rate for a specific savings goal. The details are as follows:
a. retirement account balance of approximately $536,144.37
b. The lump sum required would be approximately $60,319.79.
c. With an account balance of $536,144.37, the annual withdrawal would be approximately $46,914.90.
d. It would take approximately 16 years until the savings are depleted.
e. Through trial and error, it can be determined that an interest rate of approximately 10.47% is needed to achieve the desired savings goal.
a. The retirement account balance on the day of retirement can be calculated by using the formula for the future value of an ordinary annuity. In this case, saving $4,500 per year for 35 years with an annual interest rate of 5.5% will result in a retirement account balance of approximately $536,144.37.
b. To achieve the same retirement savings goal with a lump-sum investment today, the present value of an ordinary annuity formula can be used. The lump sum required would be approximately $60,319.79.
c. Assuming a retirement duration of 17 years and a desire to exhaust the savings with the 17th withdrawal, the annual withdrawal can be calculated using the formula for the annuity payment. With an account balance of $536,144.37, the annual withdrawal would be approximately $46,914.90.
d. If the decision is made to withdraw $90,000 per year in retirement, the number of years until the savings are exhausted can be determined using the formula for the number of periods in an annuity. It would take approximately 16 years until the savings are depleted.
e. If the maximum affordable annual saving is $900 and the goal is to retire with $1,000,000, the required interest rate can be calculated using the formula for the rate of return. Through trial and error, it can be determined that an interest rate of approximately 10.47% is needed to achieve the desired savings goal.
These calculations provide insights into the financial aspects of retirement planning and can help individuals make informed decisions about their savings, investments, and withdrawal strategies based on their specific goals and constraints.
Learn more about rate of return here:
https://brainly.com/question/30761579
#SPJ11
Solve the quadratic F(x)=x^2+10x-1
Please explain.
Answers
The solutions to the quadratic equation f(x) = x² + 10x - 1 are x = -5 + √26 and x = -5 - √26
To solve the quadratic equation f(x) = x² + 10x - 1
we can use the quadratic formula:
x = (-b ± √(b² - 4ac)) / (2a)
For the given equation, a = 1, b = 10, and c = -1.
Substituting these values into the quadratic formula:
x = (-(10) ± √((10)² - 4(1)(-1))) / (2(1))
= (-10 ± √(100 + 4)) / 2
= (-10 ± √104) / 2
Simplifying further:
x = (-10 ± 2√26) / 2
= -5 ± √26
Therefore, the solutions to the quadratic equation f(x) = x² + 10x - 1 are:
x = -5 + √26 and x = -5 - √26
To learn more on Quadratic equation click:
https://brainly.com/question/17177510
#SPJ1
Find the volume of rectangular pyramid 5in 5 in 2 in
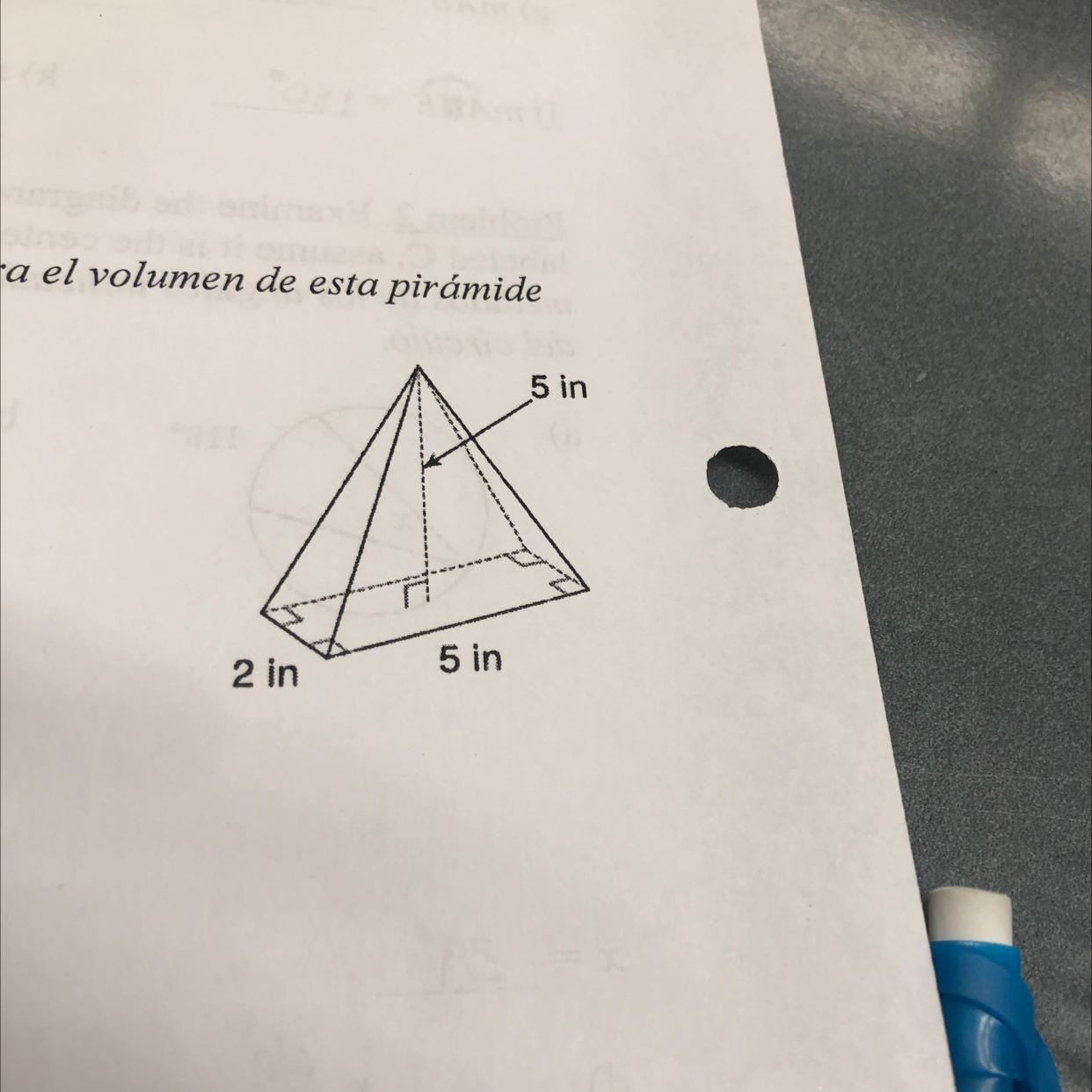
Answers
Answer:
16.67
Step-by-step explanation:
formula for a rectangular pyramid =
lengthxwidth= base area x height/3
2x5=10x5=50
50/3=16.67
In a survey of 439 teenagers in the US, 14% said that they worked during their summer vacation. a) What is the Margin of Error for this sample proportion
Answers
Answer:
\(0.0166\)
Step-by-step explanation:
Let the sample proportion be \(\hat{p}=0.14\) and the sample size be \(n=439\):
\(\displaystyle \text{Margin of Error}=\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}\\\\\text{Margin of Error}=\sqrt{\frac{0.14(1-0.14)}{439}}\\\\\text{Margin of Error}=\pm0.0166\)
Click through the graphs and select the one that could represent the relationship be
time, t, for the cell phone plan shown below.
time in hours 0 1 2 3
cost in dollars 10 13 16 19
Cost in dollars
20
18
16
14
4
2
2
3
Time in Hours
4
S
Answers
The linear function for the cost is given as follows:
C(t) = 10 + 3t.
How to define a linear function?The slope-intercept equation for a linear function is presented as follows:
y = mx + b
In which:
m is the slope.b is the intercept.We have that each hour, the cost increases by $3, hence the slope m is given as follows:
m = 3.
For a time of 0 hours, the cost is of $10, hence the intercept b is given as follows:
b = 10.
Thus the function is given as follows:
C(t) = 10 + 3t.
More can be learned about linear functions at https://brainly.com/question/15602982
#SPJ1
y2+4x2-3y2-2x
plz help
Answers
evaluate -2x + 4x2 - 2y2
Olivia has $9,050 in a savings account that earns 2.5 % annually. How much will she earn in interest in 2 years?
Answers
Answer:
452.5
Step-by-step explanation:
9050 x 0.025
226.25 x 2
452.5
Which number is a factor of 20?
Answers
Answer:
1, 2, 4, 5, 10, 20
Step-by-step explanation:
Factors of 20 will be numbers that multiply evenly into another whole number to get to 20.
Factors of 20:
1, 2, 3, 4, 5, 10, 20
negative factors of 20:
-1, -2, -3, -4, -5, -10, -20
Prime Factors of 20:
2 and 5
is this what you needed
Implement a linear time algorithm for the following problem:
Given a list A of n distinct numbers and an integer i, with 1 ≤ i ≤ n, find the element x ∈ A that is larger than exactly i − 1 other elements of A.
Hint: Note that we can solve this problem in O(n log n) time, since we can sort the numbers using QuickSort and then simply index the i th element in the output array. However, we want to do it faster. Implement the algorithm described below :
1. Divide the n elements of the input array into ⌊n/5⌋ groups of 5 elements each and at most one group made up of the remaining n mod 5 elements.
2. Find the median of each of the ⌊n/5⌋ groups by first insertion-sorting the elements of each group (of which there are at most 5) and then picking the median from the sorted list of group elements.
3. Use SELECT recursively to find the median x of the ⌊n/5⌋ medians found in step 2. (If there are an even number of medians, then by our convention, x is the lower median.)
4. Partition the input array around the median-of-medians x using the modified version of PARTITION. Let k be one more than the number of elements on the low side of the partition, so that x is the kth smallest element and there are n-k elements on the high side of the partition.
5. If i z = k, then return x. Otherwise, use SELECT recursively to find the ith smallest element on the low side if i > k
Answers
The algorithm finds the element x in a list A that is larger than exactly i - 1 other element of A using a linear time approach based on the median of medians.
1. Divide the n elements of the input array into ⌊n/5⌋ groups of 5 elements each and at most one group made up of the remaining n mod 5 elements.
2. Find the median of each of the ⌊n/5⌋ groups by first insertion-sorting the elements of each group (of which there are at most 5) and then picking the median from the sorted list of group elements.
3. Use SELECT recursively to find the median x of the ⌊n/5⌋ medians found in step 2. If there are an even number of medians, x is the lower median.
4. Partition the input array around the median-of-medians x using a modified version of the PARTITION algorithm. Let k be one more than the number of elements on the low side of the partition so that x is the kth smallest element and there are n-k elements on the high side of the partition.
5. If i = k, then return x. Otherwise, use SELECT recursively to find the ith smallest element on the low side if i > k, or on the high side if i < k.
The algorithm utilizes the concept of finding the median of medians to efficiently find the desired element. By dividing the array into groups and recursively finding the median, it effectively reduces the problem size. The partitioning step helps to narrow down the search range based on the relationship between i and k.
This algorithm guarantees the linear time complexity of O(n), making it faster than the O(n log n) time complexity achieved by sorting and indexing the array.
Learn more about linear time algorithm: https://brainly.com/question/30511610
#SPJ11
40 people were asked whether they can sew and whether they can knit. 14 of them can sew and 12 of them can knit. 5 of the people who can sew can also knit. How many of the people asked can neither sew nor knit?
Answers
Answer:
data given
Universal set 40people
people who can sew 14
people who can knit 12
people who can do both 5
Step-by-step explanation:
•people who can sew only
=14-5
=9
•people who can knit only
=12-9
=7
Union of people who can sew and the one who can knit
=9+7+5
=21
who do neither
=40-21
=19
: .people neither sew or knit are 19
Which of the coordinate points below will fall on a line where the constant of proportionality is 1/4? Select all that apply. A) (4,1) B) (8,12) C) (12,3) D) (20,5) E) (12,6)
Answers
Answer:
A) (4,1) C) (12,3) D) (20,5)
Step-by-step explanation:
Required
Which has a constant of proportionality of 1/4
To solve this, we make use of:
\(y = kx\)
Where k is the constant of proportionality.
Solve for x
\(k = y/x\)
Testing the given options
A) (4,1)
\(k = y/x\)
\(k =1/4\)
B) (8,12)
\(k = y/x\)
\(k =12/8\)
\(k =3/2\)
C) (12,3)
\(k = y/x\)
\(k = 3/12\)
\(k = 1/4\)
D) (20,5)
\(k = y/x\)
\(k = 5/20\)
\(k = 1/4\)
E) (12,6)
\(k = y/x\)
\(k =6/12\)
\(k =1/2\)
The owner of a flower shop on H street sells 28 roses for $140. What is the cost in dollars per rose?
Answers
Answer:
$5 ( sorry if it is incorrect)
Step-by-step explanation:
Which equations have the same value of x as Three-fifths (30 x minus 15) = 72? Select three options.
a.18 x minus 15 = 72
b.50 x minus 25 = 72
c.18 x minus 9 = 72
d.3 (6 x minus 3) = 72
e.x=4.5
Answers
Answer:
C, D and E
Step-by-step explanation:
Given equation:
\(\dfrac35(30x-15)=72\)
Use the distributive law \(a(b-c)=ab-ac\):
\(\implies \dfrac35\cdot30x- \dfrac35\cdot15=72\)
\(\implies \dfrac{3 \cdot30}5x- \dfrac{3 \cdot15}5=72\)
\(\implies \dfrac{90}5x- \dfrac{45}5=72\)
\(\implies 18x- 9=72\) ← option c
Factor out common term 3:
\(\implies 3(6x- 3)=72\) ← option d
Solve \(18x- 9=72\):
\(\implies 18x- 9+9=72+9\)
\(\implies 18x=81\)
\(\implies \dfrac{18x}{18}=\dfrac{81}{18}\)
\(\implies x=4.5\) ← option e
julian needs to spend at least seven hours each week practicing the drums. he has already practiced five and one third hours this week. he wants to sp
Answers
The minimum number of hours is 5/6 and the inequality is x ≥ 5/6 hours.
What exactly is an inequality?An inequality is a relationship that compares two numbers and perhaps other mathematical expressions that are not equal. It is most commonly used to compare the sizes of two numbers on a number line.
According to the given data:Let x = the number of hours practicing the drums
we know that Julian needs to spend at least seven hours each week practicing
the drums x ≥ 7 hours
He has already practiced 5*(1/3) hours this week.
Convert mixed number to an improper fraction 5*(1/3) = 16/3hours.
Subtract 16/3 from 7,
7 - (16/3)
= 5/3
Divide 5/3 by 2,
(5/3)/2
=5/6
Hence,
The inequality that represent the minimum number of hours he needs to practice on each of the two days is x ≥ 5/6 hours.
To learn more about inequality visit:
https://brainly.com/question/20383699
#SPJ4
The given question is not complete.
Julian needs to spend at least seven hours each week practicing the drums. He has already practiced 5 1/3 hours this week. He wants to split the remaining practice time evenly between the last two days of the week. Write an inequality to determine the minimum number of hours he needs to practice on each of the two days.
I need help pleaseeeee

Answers
Answer:
C. 8.66 in
Step-by-step explanation:
Using the formula of circumference of a circle
\(2\pi \: r \)
then,
first find r by plagging in the given data.
so, r = 4.33 in
since it's diameter needed, then
r + r = d
4.33 in + 4.33 in = 8.66 in
Consider this system of equations.
p=2n
p-5 = 1. 5n
What value of n makes the system of equations true?
Enter your answer in the box.
Answers
Therefore, the value of n that makes the system of equations true is n = 10.
Given:
p = 2n
p - 5 = 1.5n
Substituting the value of p from the first equation into the second equation, we have:
2n - 5 = 1.5n
Next, we can solve for n by subtracting 1.5n from both sides of the equation:
2n - 1.5n - 5 = 0.5n - 5
Simplifying further:
0.5n - 5 = 0
Adding 5 to both sides of the equation:
0.5n = 5
Dividing both sides by 0.5:
n = 10
Therefore, the value of n that makes the system of equations true is n = 10.
Learn more about equations here
https://brainly.com/question/29657992
#SPJ11
what is 7/9 divided by 6/8
Answers
Answer: \(\frac{28}{27}\) or \(1\frac{1}{27}\)
Step-by-step explanation:
\(\frac{7}{9} /\frac{6}{8} = \frac{7}{9}(\frac{8}{6})\)
\(\frac{7}{9} (\frac{8}{6} ) = \frac{28}{27}\)
\(\frac{28}{27} = 1 \frac{1}{27}\)
15) The Comic Depot gives customers a free comic book when they purchase 9 comic books. How many free comic books can Marci get if she buys 68 comics? * O 7 free comic books O 5 free comic books O 8 free comic books fine comic books
Answers
Marci can get 7 free comic books if she buys 68 comics. Therefore, option A, "7 free comic books" is the correct answer.
According to the question, the Comic Depot gives one free comic book to customers when they purchase 9 comic books. This means that a customer who buys 9 comic books gets one comic book for free. If a customer buys 18 comic books, he/she will get two comic books for free, and so on. We can find the relationship between the number of comic books a customer buys and the number of free comic books he/she gets by using a unitary method.
Let x be the number of comic books Marci buys and let y be the number of free comic books she gets. Since Marci gets one free comic book for every nine comic books she buys, we have that:
y = (1/9) x.
Rearranging the equation above to solve for x, we have that:
x = 9y
We are asked to find the number of free comic books Marci can get if she buys 68 comic books. Thus, we substitute x = 68 into the equation above to find the number of free comic books y:
y = (1/9)68 = 7.56
Thus, Marci can get 7 free comic books.
Learn more about unitary method visit:
brainly.com/question/14793162
#SPJ11
Builtrite has calculated the average cash flow to be $14,000 with a standard deviation of $5000. What is the probability of a cash flow being between than $16,000 and $19,000 ? (Assume a normal distribution.) 16.25% 18.13% 23.90% 2120%
Answers
The correct answer is that the probability of a cash flow being between $16,000 and $19,000 is approximately 18.59%.
To calculate the probability of a cash flow being between $16,000 and $19,000, we can use the standard deviation and assume a normal distribution.
We are given that the average cash flow is $14,000 with a standard deviation of $5,000. These values are necessary to calculate the probability.
The probability of a cash flow falling within a certain range can be determined by converting the values to z-scores, which represent the number of standard deviations away from the mean.
First, we calculate the z-score for $16,000 using the formula: z = (x - μ) / σ, where x is the cash flow value, μ is the mean, and σ is the standard deviation. Plugging in the values, we get z1 = (16,000 - 14,000) / 5,000.
z1 = 2,000 / 5,000 = 0.4.
Next, we calculate the z-score for $19,000: z2 = (19,000 - 14,000) / 5,000.
z2 = 5,000 / 5,000 = 1.
Now that we have the z-scores, we can use a standard normal distribution table or calculator to find the corresponding probabilities.
Subtracting the probability corresponding to the lower z-score from the probability corresponding to the higher z-score will give us the probability of the cash flow falling between $16,000 and $19,000.
Looking up the z-scores in a standard normal distribution table or using a calculator, we find the probability for z1 is 0.6554 and the probability for z2 is 0.8413.
Therefore, the probability of the cash flow being between $16,000 and $19,000 is 0.8413 - 0.6554 = 0.1859, which is approximately 18.59%.
So, the correct answer is that the probability of a cash flow being between $16,000 and $19,000 is approximately 18.59%.
To learn more about probability click here:
brainly.com/question/31828911
#SPJ11
The probability of a cash flow between $16,000 and $19,000 is approximately 18.59%.
To calculate the probability of a cash flow being between $16,000 and $19,000, we can use the standard deviation and assume a normal distribution.
We are given that the average cash flow is $14,000 with a standard deviation of $5,000. These values are necessary to calculate the probability.
The probability of a cash flow falling within a certain range can be determined by converting the values to z-scores, which represent the number of standard deviations away from the mean.
First, we calculate the z-score for $16,000 using the formula: z = (x - μ) / σ, where x is the cash flow value, μ is the mean, and σ is the standard deviation. Plugging in the values, we get z1 = (16,000 - 14,000) / 5,000.
z1 = 2,000 / 5,000 = 0.4.
Next, we calculate the z-score for $19,000: z2 = (19,000 - 14,000) / 5,000.
z2 = 5,000 / 5,000 = 1.
Now that we have the z-scores, we can use a standard normal distribution table or calculator to find the corresponding probabilities.
Subtracting the probability corresponding to the lower z-score from the probability corresponding to the higher z-score will give us the probability of the cash flow falling between $16,000 and $19,000.
Looking up the z-scores in a standard normal distribution table or using a calculator, we find the probability for z1 is 0.6554 and the probability for z2 is 0.8413.
Therefore, the probability of the cash flow being between $16,000 and $19,000 is 0.8413 - 0.6554 = 0.1859, which is approximately 18.59%.
So, the correct answer is that the probability of a cash flow being between $16,000 and $19,000 is approximately 18.59%.
To learn more about probability click here:
brainly.com/question/31828911
#SPJ11
Find the slope of the line that passes through (7,5) and (5, 4).
Simplify your answer and write it as a proper fraction, improper fraction, or integer.
Answers
Answer:
y = 1/2x + 3/2
Step-by-step explanation:
Slope m = (y2-y1)/(x2-x1)
m = (4 - 5)/(5 - 7)
m = (-1)/(-2)
m = 1/2
Slope-intercept: y = mx + b
y = 1/2x + b
using (5,4)
4 = 1/2(5) + b
4 = 5/2 + b
b = 4 - 5/2 = 8/2 - 5/2 = 3/2
then y = 1/2x + 3/2
How do you put 0.02 in scientific notation
Answers
Answer:
2 x 10^-2
Step-by-step explanation:
0.02 equals to 2/100
therefore 0.02= 2/102 (remember this is negative)
= 2x10^-2 (therefore -2)
The solution to the number 0.02 in scientific notation is 2 * 10⁻²
How to express the number 0.02 in scientific notationFrom the question, we have the following parameters that can be used in our computation:
Number = 0.02
Multiply the number by 1
So, we have
Number = 0.02 * 1
Express 1 as 100/100
So, we have the following representation
Number = 0.02 * 100/100
Next, we have
Number = 2 * 1/100
Express 1/100 as 10⁻²
So, we have
Number = 2 * 10⁻²
Hence, the solution is 2 * 10⁻²
Read more about scientific notation at
brainly.com/question/1767229
#SPJ6
what is the answer?

Answers
Answer:
5
Step-by-step explanation:
Plz mark brainliest!!!
the question is in the attached file

Answers
Answer:
C
Step-by-step explanation:
using
x × y = \(\sqrt{x^2+y^2}\) , then
2 × 4\(\sqrt{2}\)
= \(\sqrt{2^2+(4\sqrt{2})^2 }\)
= \(\sqrt{4+32}\)
= \(\sqrt{36}\)
= 6
\(\textsf {Applying this formula :}\)
\(\mathsf {(x) \times (y) =\sqrt{x^{2} + y^{2}}}\)
\(\textsf {Now take :}\)
\(\mathsf {x = 2}\\\mathsf {y = 4\sqrt{2}}\)
\(\mathsf {Solving :}\)
\(\implies \mathsf {\sqrt{(2)^{2} + (4\sqrt{2})^{2}}}\)
\(\implies \mathsf {\sqrt{4 + 32}}\)
\(\implies \mathsf {6}\)
Convert the following equations from point-slope form to slope-intercept form.
9) y – 4 = 3(x – 1)
10) y – 1 = -4(x – (-3))
Answers
We need to solve both for y.
#9:
\(y - 4 = 3(x - 1)\\\\y - 4 = 3x - 3\\\\y = 3x + 1\)
#10:
\(y - 1 = -4[x - (-3)]\\\\y - 1 = -4(x + 3)\\\\y - 1 = -4x - 12\\\\y = -4x - 11\)
C^3 + 5 / c+4 Long division
Answers
Using the long division we get:
Therefore:
\(\frac{c^3+5}{c+4}=c^2-4c+16-\frac{59}{c+4}.\)Answer:
\(\frac{c^3+5}{c+4}=c^2-4c+16-\frac{59}{c+4}.\)
