write 5 3/4 as an improper fraction .
Answers
Answer:
15/4
Step-by-step explanation:
Answer:
\(\frac{23}{4}\)
Step-by-step explanation:
5 \(\frac{3}{4}\) = \(\frac{5 x 4 + 3 }{4}\) = \(\frac{23}{4}\)
Hope is right!!!
Related Questions
guess the value of the limit lim x→[infinity] x2 2x by evaluating the function f(x) = x2/2x for x = 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 20, 50, and 100. use a graph of f to support your guess.
Answers
To guess the value of the limit lim x→∞ (x²)/(2x), we can evaluate the function f(x) = (x²)/(2x) for the given x values and analyze the graph of f(x).
1. Evaluate f(x) for x = 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 20, 50, and 100.
2. Plot the points on a graph to visualize the function's behavior as x approaches infinity.
By evaluating f(x) at the given points, we can observe that the function f(x) simplifies to f(x) = x/2, as the x in the numerator and denominator cancels out. As x increases, the function also increases, and there's no limit to how large x can become. Therefore, the limit as x approaches infinity is also infinity. The graph of f(x) supports this observation, as it shows a straight line with a positive slope, indicating that the function will continue to grow without bound as x approaches infinity.
The limit lim x→∞ (x²)/(2x) is infinity.
To know more about numerator and denominator visit:
brainly.com/question/15007690
#SPJ11
a rectangle is drawn so the width is 16 inches longer than the height. if the rectangle's diagonal measurement is 80 inches, find the height.
Answers
Hope this helped
An exam consists of 40 multiple-choice questions. Each question has a choice of five answers, only one of which is correct. For each correct answer, a candidate gets 1 mark, and no penalty is applied for getting an incorrect answer. A particular candidate answers each question purely by guess-work. Using Normal approximation to Binomial distribution with continuity correction, what is the estimated probability this student obtains a score greater than or equal to 10? Please use R to obtain probabilities and keep at least 6 decimal places in intermediate steps.
A. 0.7234 B. 0.2766 C. 0.5927 D. 0.1615 E. 0.3773
Answers
The estimated probability that the candidate obtains a score greater than or equal to 10 is 0.7234, rounded to four decimal places, so the answer is (A).
The number of correct answers that the candidate gets is a binomial random variable with parameters n = 40 (number of trials) and p = 1/5 (probability of success). We want to find the probability that the candidate gets a score greater than or equal to 10, which is equivalent to getting 10 or more questions correct.
Using the normal approximation to the binomial distribution with continuity correction, we can approximate the distribution of the number of correct answers by a normal distribution with mean μ = np = 40 * 1/5 = 8 and variance σ^2 = np(1-p) = 40 * 1/5 * 4/5 = 6.4.
To find the probability that the candidate gets 10 or more questions correct, we can standardize the normal distribution and use the standard normal distribution table or R to find the probability.
Let X be the number of correct answers. Then, we have:
P(X >= 10) = P((X - μ) / σ >= (10 - μ) / σ)
= P(Z >= (10 - 8) / sqrt(6.4)), where Z is a standard normal random variable.
For more similar questions on probability:
brainly.com/question/13604758
#SPJ11
What is the term for breaking a larger number apart into smaller numbers that can be multiplied together to get a specific result?.
Answers
Distributive property is the term for breaking a larger number apart into smaller numbers that can be multiplied together to get a specific result.
What is distributive property?Firstly, to distribute means to divide something or give a share or part of something.
Distributive property explains that multiplying the sum of two or more addends by a number will give the same result as multiplying each addend individually by the number and then adding the products together.
Therefore, distributive property is the term for breaking a larger number apart into smaller numbers that can be multiplied together to get a specific result.
Learn more about distributive property at: https://brainly.com/question/5637942
#SPJ1
Twenty-three people purchae raffle ticket. Three winning ticket are elected at random. If firt prize i $4000, econd prize i $3500 , and third prize i $400, in how many different way can the prize be awarded?
Answers
Hence, the prizes can be distributed in 10626 ways.
Permutation and combination are the ways to represent a group of objects by selecting them in a set and forming subsets. It defines the various ways to arrange a certain group of data. When we select the data or objects from a certain group, it is said to be permutations, whereas the order in which they are represented is called combination.
The total number of people purchasing tickets=23
The total number of prizes = 3
Since, order matters here, so we use Permutations.
The permutation of n things taken r at a time is given by:-
\(^np_r=\frac{n!}{(n-r)!}\)
Then, the number of ways the prizes can be distributed-
\(^{23}p_3=\frac{23!}{(23-3)!}\\\\=23*22*21=10626\)
Hence, the prizes can be distributed in 10626 ways.
learn more about Permutation,
https://brainly.com/question/1216161
#SPJ4
find the domain of the function f(x, y) = ln(3 − x 2 − 4y 2 )
Answers
The domain of the function f(x, y) is all the values of x and y that make the argument of the natural logarithm function greater than zero. Thus, the domain of f(x, y) is the set of all ordered pairs (x, y) such that 3 - x^2 - 4y^2 > 0.
The natural logarithm function is defined only for positive values, so for f(x, y) to be defined, the expression inside the logarithm must be greater than zero. Solving the inequality 3 - x^2 - 4y^2 > 0 for x^2 and y^2 separately, we get x^2/3 + y^2/3 < 1, which represents an ellipse with center (0,0), semi-major axis of length sqrt(3) in the x-direction, and semi-minor axis of length sqrt(3)/2 in the y-direction. Therefore, the domain of f(x, y) is the interior of this ellipse.
You can learn more about domain at
https://brainly.com/question/28934802
#SPJ11
if f(x) = -x^2+4x-9 and g(x) = x - 8 find g(f(-1)).
Answers
Answer: g(f(-1))=-22
Step-by-step explanation:
To find g(f(-1)), you want to first want to solve f(-1). Once you solved that, you plig the answer you get into g(x). Then, you will have your final answer.
f(-1)=-(-1)²+4(-1)-9 [exponent]
f(-1)=-1+4(-1)-9 [multiply]
f(-1)=-1-4-9 [subtract from left to right]
f(-1)=-14
We have found that f(-1)=-14. Now, we know in -14 into g(x) and solve.
g(-14)=(-14)-8 [subtract]
g(-14)=-22
Now, we know that g(f(-1))=-22.
Help me with this please :)

Answers
Answer:
Hey there!
X+Y=0.
For example, two numbers that are equally far from the 0 on a number line are -2 and 2.
-2+2=0
Hope this helps :)
Answer:
x + y = 0
Step-by-step explanation:
Since the two values are the same distance from zero on the number line (i.e., they are equivalent in distance) and one is in the negative direction, and the other is in the positive direction, then the sum of both will be zero.
Since they are the same distance, just opposite in direction, it requires the same amount of "hops" for both values to reach zero, hence they will cancel each other out when added together.
Consider, -1 and 1. Both are the same distance from 0; however, if you add them together (-1 + 1) you'll get the sum to be 0.
Cheers.
Answer this to get 10 points + BRAINLIEST!!!!!
Paragraph Five
As a member of the Feel Power.org team, Noah explains, "I like to teach kids because I feel like I have good mentors in my life. A lot of kids don't have that, and I want to be a mentor for them. We go to schools and teach kids how to be respectful and how to make positive life choices." The goal of Feel the Power is to "give youth the skills they need to make positive life choices." Noah and others visit schools and talk to students about respect, responsibility, honesty, and being drug free. He received recognition for his "Respect" video that helps people confront the issue of bullying.
In paragraph 5, the author of the article lists the topics that Noah and the Feel the Power team discuss in their motivational talks. What do the selected topics imply about the organization's beliefs?
A) These areas are necessary for a successful life.
B) These areas are necessary for a successful life.
C) These qualities are the easiest to teach others.
D) These are areas of life where people do not need help.
Answers
Answer:
A&B
Step-by-step explanation:
Because by going through this paragraph the closest answer is that these are necessary steps to ensure that the youth have successful lives.
check the attached picture, please help me out ! thanks in advance
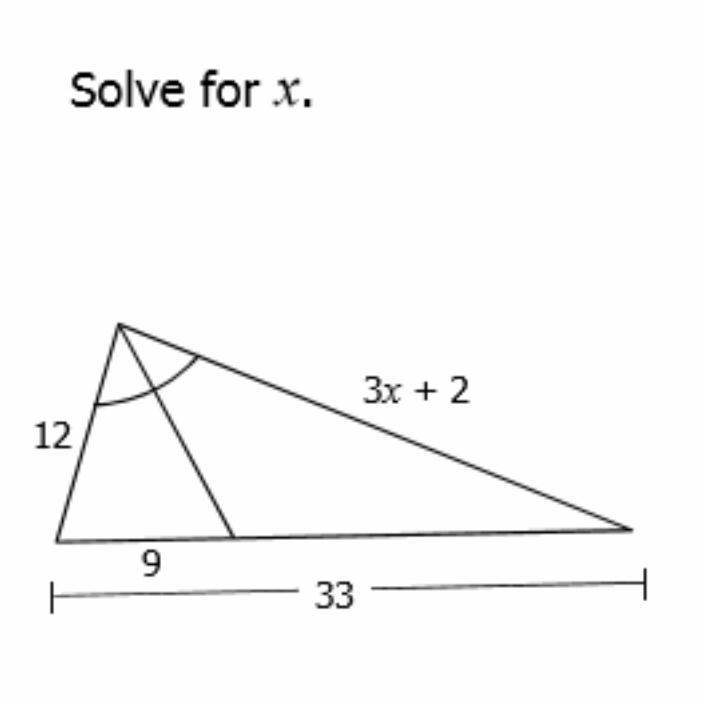
Answers
Answer:
x = 10.
Step-by-step explanation:
As the 2 angles at the vertex are congruent we can say that:
12 / 3x + 2 = 9 / (33-9)
12/3x+2 = 9/24 = 3/8
3(3x+2) = 12*8
9x + 6 = 96
9x = 90
x = 10.
Sirius has a right ascension of 06h 45m and declination of −16°
43′. Calculate the local hour angle of Sirius when local sidereal
time is 03h 00m.
Answers
The local hour angle of Sirius when the local sidereal time is 03h 00m is approximately -56.25 degrees.
To find the local hour angle of Sirius, we need to determine the difference between the local sidereal time and the right ascension of Sirius. The local sidereal time represents the hour angle of the vernal equinox, which is the point in the sky where the Sun crosses the celestial equator from south to north during the spring equinox.
We have,
Right Ascension of Sirius = 06h 45m
Declination of Sirius = -16° 43'
First, we need to convert the right ascension of Sirius into degrees. Since there are 24 hours in a full circle, each hour corresponds to 15 degrees (360°/24h). Each minute of right ascension corresponds to 0.25 degrees (15°/60m).
Right Ascension of Sirius in degrees:
= (6 hours * 15 degrees/hour) + (45 minutes * 0.25 degrees/minute)
= 90 degrees + 11.25 degrees
= 101.25 degrees
Next, we need to convert the local sidereal time into degrees. Since there are 24 hours in a full circle, each hour corresponds to 15 degrees.
Local Sidereal Time in degrees:
= 3 hours * 15 degrees/hour
= 45 degrees
Finally, we can calculate the local hour angle of Sirius by subtracting the right ascension of Sirius from the local sidereal time.
Local Hour Angle of Sirius:
= Local Sidereal Time - Right Ascension of Sirius
= 45 degrees - 101.25 degrees
= -56.25 degrees
The local hour angle of Sirius when the local sidereal time is 03h 00m is approximately -56.25 degrees.
To know more about right ascension and declination, refer here:
https://brainly.com/question/207368#
#SPJ11
The quadratic equation x x4 3 2 0 2 − − = has what roots
Answers
The quadratic equation x2 - 4x + 3 = 0 has two roots. The roots are given by the quadratic formula as x = [4 ± √(16 - 12)]/2, which gives x = [4 ± 2√3]/2. Therefore, the roots are x = 2 ± √3.
The quadratic equation x^2 - 4x - 3 = 0 has two roots.
To find the roots of this equation, we can use the quadratic formula:
x = (-b ± √(b^2 - 4ac))/(2a)
In this case, a = 1, b = -4, and c = -3. Plugging these values into the quadratic formula, we get:
x = (-(-4) ± √((-4)^2 - 4(1)(-3)))/(2(1))
x = (4 ± √(16 + 12))/2
x = (4 ± √28)/2
x = (4 ± 2√7)/2
Simplifying further, we get:
x = 2 ± √7
Therefore, the two roots of the equation are x = 2 + √7 and x = 2 - √7.
Learn more about quadratic equation here: brainly.com/question/24349828
#SPJ11
Does anyone know what 6.04 x 10^-3
Answers
Answer:
.00604
Step-by-step explanation:
when multiplying by a negative exponent move the decimal to the left
10^-3 move the decimal 3 spaces to left
.00604
Select all sets in which the number -3/4
is an element
A. rational numbers
B. integers
C. natural numbers
D. whole numbers
E. irrational numbers
Freal numbers
Answers
Answer:
Rational numbers is the correct answer for this.
Step-by-step explanation:
Rational numbers is the best and correct answer.
A track coach records the number of miles that he ran per day over the month. The stem-and-leaf plot below summarizes this data.
Answers
Answer:
\(Mean = 6.70\)
Step-by-step explanation:
Given
See attachment for plot
Required
The mean of the plot
Mean is calculated as:
\(Mean = \frac{\sum x}{n}\)
Where
\(n = 20\)
Using the given key to read, the plot;
We have:
\(Mean = \frac{3.00+3.25+4.25+5.00+..........+8.75+9.50}{20}\)
\(Mean = \frac{134.00}{20}\)
\(Mean = 6.70\)

need help finding area

Answers
From 50 ft. to 75 ft.
Answers
Answer:
25 ft.
Step-by-step explanation:
what two numbers multiply make 54 and added together make 15
Answers
Answer:6 and 9
Step-by-step explanation:
6*9= 54
6+9=15
Answer:
6, 9
Step-by-step explanation:
You want the numbers that have a product of 54 and a sum of 15.
Divisors of 54The prime factors of 54 are ...
54 = 2 · 3³
Adding 1 to the exponents, we have (1, 3) +(1, 1) = (2, 4). The product of these increased exponents is 2·4 = 8, which means there are 8 divisors of 54, including 1 and 54.
We can write the factor pairs as ...
54 = 1·54 = 2·27 = 3·18 = 6·9
The sums of these divisor pairs are 55, 29, 21, 15
The two numbers you seek are 6 and 9.
__
Additional comment
The reason for figuring the number of divisors is so we can check to make sure we have found factor pairs for all of them. The 8 divisors give us 8/4 = 4 factor pairs. We have found it is usually easier to find the desired sum once we have the list of factor pairs for a number.
The smallest sum of two factors will be 2√54 ≈ 14.7. This tells you that the sum of 15 will involve factors that are close to √54 ≈ 7.4. You find the factors of interest when you consider divisors that are near 7: 6 and 9.
You may have noticed it is very helpful to have a great command of your multiplication facts when working problems of this sort.
A graph can provide a quick solution, too.
#95141404393

what's the difference between the arithmetic and geometric average return (conceptually, not mathematically), and when is it best to use each?
Answers
Conceptually, the arithmetic and geometric average returns are different measures used to describe the performance of an investment or an asset over a specific period.
The arithmetic average return, also known as the mean return, is calculated by adding up all the individual returns and dividing by the number of periods. It represents the average return for each period independently.
On the other hand, the geometric average return, also called the compound annual growth rate (CAGR), considers the compounding effect of returns over time. It is calculated by taking the nth root of the total cumulative return, where n is the number of periods.
When to use each measure depends on the context and purpose of the analysis:
1. Arithmetic Average Return: This measure is typically used when you want to evaluate the average return for each individual period in isolation. It is useful for analyzing short-term returns, such as monthly or quarterly returns. The arithmetic average return provides a simple and straightforward way to assess the periodic performance of an investment.
2. Geometric Average Return: This measure is more suitable when you want to understand the compounded growth of an investment over an extended period. It is commonly used for long-term investment horizons, such as annual returns over multiple years.
The geometric average return provides a more accurate representation of the overall growth rate, accounting for the compounding effect and reinvestment of returns.
In summary, the arithmetic average return is suitable for analyzing short-term performance, while the geometric average return is preferred evaluating long-term growth and the compounding effect of returns.
learn more about Average Return here:
https://brainly.com/question/29662426
#SPJ11
PLEASE HELP ME ! :3
How do you write an equation in standard form?
Answers
Answer:
The standard form is just another way to write this equation, and is defined as Ax + By = C, where A, B, and C are real numbers, and A and B are both not zero (see note below about other requirements). As you will see in the lesson below, every line can be expressed in this form.
The "Standard Form" of an equation is: (some expression) = 0 In other words, "= 0" is on the right, and everything else is on the left. Example: Put x 2 = 7 into Standard Form
Step-by-step explanation:
sorry look up example image for standard form
You weigh six packages and find the weights to be 20, 12, 52, 16, 48, and 44 ounces. If you include a package that weighs 60 ounces, which will increase more, the median or the mean?
Answers
Answer:
median
Step-by-step explanation:
The first step is to sort the numbers from largest to smallest (you could go the other way as well).
60 52 48 44 20 16 12
The median is the middle number 44 in this case. The median has 3 numbers on its left and 3 on its right (in this case). 44 has 60 52 48 or its left and 20 16 and 12 on its right.
The mean is the average. We'll call it the new average
The mean is 60 + 52 + 48 + 44 + 20 + 16 + 12 = 252
The new mean is 252 / 7 = 36
=====================
The old median is the average between the middle 2 numbers (before you added 60 you had 6 numbers)
52 + 48 + 44 + 20 + 16 + 12 = the average of 44 + 20 which 64/2 = 32
The old mean was (52 + 48 + 44 + 20 + 16 + 12)/6 = 32.
=======================
The median increased from 44 to 32 = 12
The mean went from 32 to 36 which is 4
Answer: the median increased more
a census of the labor force in a large metropolitan area found that the time it takes for people to commute to work has a mean of 20.5 minutes and a standard deviation of 15.4 minutes. what is the probability that a random sample of 40 people have a mean commute time that is greater than 25 minutes?
Answers
the probability of a standard normal random variable being greater than 1.84 is approximately 0.0336.
We can use the central limit theorem to answer this question. The central limit theorem states that if we have a large enough sample size, the distribution of sample means will be approximately normal, even if the population distribution is not normal. The sample mean is given by:
X = μ
where X is the sample mean, μ is the population mean, and n is the sample size.
In this case, we have a sample size of n = 40, and we want to know the probability that the sample mean is greater than 25 minutes. We can standardize the sample mean using the standard error of the mean, which is given by:
SE = σ / sqrt(n)
where σ is the population standard deviation. In this case, σ = 15.4 minutes, so:
SE = 15.4 / sqrt(40) = 2.44 minutes
We can then calculate the z-score for the sample mean:
z = (X - μ) / SE = (25 - 20.5) / 2.44 = 1.84
Using a standard normal distribution table or calculator, we can find that the probability of a standard normal random variable being greater than 1.84 is approximately 0.0336. This means that the probability of a random sample of 40 people having a mean commute time that is greater than 25 minutes is approximately 0.0336, or 3.36%.
In summary, we used the central limit theorem to approximate the distribution of sample means, calculated the standard error of the mean and the z-score for the sample mean, and used a standard normal distribution table or calculator to find the probability of the sample mean being greater than 25 minutes.
To know more about standard normal distribution click here:
brainly.com/question/29509087
#SPJ4
Amy gets a new kennel for her dog. A sketch of the kennel is shown here. If the roof is in the shape of a triangular prism (bottom face included), what is the surface area of the roof of the kennel, including the bottom face?
Answers
Answer:
Surface area of the roof of the kennel, including the bottom face is 58.96 ft^2
Step-by-step explanation:
The image is attached below
For the triangular sides of the roof, area is
A = \(\frac{1}{2}bh\)
where b is the base = 4 ft
h is the vertical height = 2.24 ft
A = \(\frac{1}{2}*4*2.24 =\) 4.48 ft^2
for the two faces we have 2 x 4.48 ft^2 = 8.96 ft^2
For the rectangular sections of the roof, area is
A = \(lh\)
where \(l\) is the length of the rectangle = 5 ft
h is the height of the rectangle = 3 ft
A = 5 x 3 = 15 ft^2
For the two rectangular faces, we have 2 x 15 ft^2 = 30 ft^2
For the bottom face, area is
A = \(lw\)
where \(l\) is the length of the house = 5 ft
w is the width of the house = 4 ft
A = 5 x 4 = 20 ft^2
Surface area of the roof of the dog kennel is
8.96 ft^2 + 30 ft^2 + 20 ft^2 = 58.96 ft^2

f(x) = x 0 (9 − t2) et2 dt, on what interval is f increasing? (enter your answer using interval notation.)
Answers
The interval on which f(x) is increasing is (-3, 3).
To determine on what interval the function f(x) = x 0 (9 − t2) et2 dt is increasing, we need to find the derivative of f(x) and then examine its sign.
We can use the Leibniz rule to find the derivative of f(x):
f'(x) = (d/dx) x 0 (9 − t2) et2 dt = (9 − x2) ex2
Now we need to determine the sign of f'(x) on different intervals. Notice that the factor (9 - x^2) is always positive for x in the interval [-3, 3], and ex^2 is always positive for any x. Therefore, the sign of f'(x) is determined by the sign of (9 - x^2)ex^2.
If x < -3 or x > 3, then (9 - x^2) is negative, and so is f'(x). Therefore, f(x) is decreasing on (-∞, -3) and (3, ∞).
If -3 < x < 3, then (9 - x^2) is positive, and so is f'(x). Therefore, f(x) is increasing on (-3, 3).
Therefore, the interval on which f(x) is increasing is (-3, 3).
Learn more about interval here:
https://brainly.com/question/13708942
#SPJ11
can someone please help me :(((((((

Answers
Answer:
D
Step-by-step explanation:
Answer:
C) 3
Step-by-step explanation:
combine like terms
=> \(x^{2+3}\) × \(y^{2+?}\) = \(x^{5}y^{5}\)
=> \(x^{5} y^{2+?}\) = \(x^{5}y^{5}\)
divide \(x^{5}\) on both side to eliminate x
=> \(y^{2+?}\) = \(y^{5}\)
=> \(y^{2+3}\) = \(y^{5}\)
=> \(y^{5}\) = \(y^{5}\)
When x³-2x^2-15x is factored completely, which expression is one of the factors?
A. X-5
B. x + 5
C. x2 – 5x
D. x2-2x-15
Answers
When x³-2x^2-15x is factored completely, one of the factors is x-5.
To factor the expression, we can use the method of grouping. We can rewrite the expression as follows:
x³-2x^2-15x = (x³-2x^2) - 15x
We can then factor the first two terms using the difference of squares:
x³-2x^2-15x = (x-2)(x^2+2x) - 15x
We can then factor the last term using the difference of squares:
x³-2x^2-15x = (x-2)(x^2+2x) - (5)(3x)
Then, we can combine the two factors to get the final answer:
x³-2x^2-15x = (x-5)(x^2+2x-3x)
The final factorization is:
x³-2x^2-15x = (x-5)(x^2-x)
So, the correct answer is (A) x-5.
does stretching help sprinters run faster? a researcher tested the null hypothesis that average sprinting times among atheltes who stretched before an event is equal to average sprinting times among those who did not stretch before an even.
Answers
The researcher tested the null hypothesis that there is no difference in average sprinting times between athletes who stretched before an event and those who did not stretch.
To determine if stretching helps sprinters run faster, the researcher formulated a null hypothesis. The null hypothesis states that there is no significant difference in average sprinting times between athletes who stretched before an event and those who did not stretch.
To test this hypothesis, the researcher would conduct an experiment where they divide the sprinters into two groups: one group that stretches before the event and another group that does not stretch. The sprinters in both groups would then compete in the sprinting event, and their times would be recorded.
After collecting the data, the researcher would compare the average sprinting times of the two groups using statistical analysis. If the analysis shows that the difference in average times between the groups is not statistically significant, meaning that it could have occurred by chance, then the null hypothesis would be supported. This would suggest that stretching before a sprinting event does not have a significant impact on sprinting times.
However, if the analysis reveals a statistically significant difference in average times between the groups, it would reject the null hypothesis. This would provide evidence that stretching does affect sprinting performance, and the researcher could conclude that stretching helps sprinters run faster based on the observed data.
Learn more about hypothesis here:
brainly.com/question/30821298
#SPJ11
Help if you know the answer it due ASAP

Answers
Answer: ∠2 and ∠7
Step-by-step explanation:
Alternate exterior angles are a pair of angles on the outer side of each of the parallel lines but on opposite sides of the transversal.
Hope I helped!
Question 7 *
2 points
Consider five-digit integers that have the following properties. Each of the digits is
1, 2 or 3, and each of 1, 2, 3 occurs at least once as a digit; also, the number is not
divisible by 2 nor divisible by 3.
What is the difference between the largest and the smallest of these integers?
O
Answers
Answer:
22098
Step-by-step explanation:
You want the difference between the largest and smallest 5-digit numbers whose digits are from the set {1, 2, 3} and include each of these at least once. The numbers cannot be divisible by 2 or 3.
DigitsThe number will be divisible by 3 when its sum of digits is a multiple of 3. Since 1, 2, and 3 are prescribed digits, the remaining two digits must not have a total of 3 or 6. The largest possible remaining digits are {2, 3}, and the smallest remaining digits are {1, 1}. (Using {3, 3} for the largest digits would give a number divisible by 3.)
The number will be divisible by 2 if the least significant digit is 2. The largest and smallest digits are not 2, so that will not be an issue.
LargestThe largest number will place the largest available digit in the place with the highest place value: 33221.
SmallestThe smallest number will place the smallest available digit in the place with the highest place value: 11123.
DifferenceThe desired difference is the difference of these numbers:
33221 -11123 = 22098 . . . . difference of largest and smallest
The difference between the two numbers will be 1998.
What is a number system?A numeral system is a writing system for expressing numbers; that is, a mathematical notation for representing numbers of a given set in a consistent manner using digits or other symbols. In different numeral systems, the same sequence of symbols can represent different numbers.
Given that Consider five-digit integers that have the following properties. Each of the digits is 1, 2 or 3, and each of 1, 2, 3 occurs at least once as a digit; also, the number is not divisible by 2 nor divisible by 3.
The largest number will be 3211.
The smallest number will be 1213.
The difference between the largest and the smallest number will be calculated as,
D = 3211 - 1213
D = 1998
To know more about the number system follow
https://brainly.com/question/17228119
#SPJ1
show that if a is both diagonalizable and invertible then so is a^-1
Answers
If a matrix A is both diagonalizable and invertible, then its inverse A^-1 is also diagonalizable.
Diagonalizable matrices can be expressed in diagonal form by a similarity transformation using a diagonal matrix. In other words, if A is diagonalizable, there exists an invertible matrix P and a diagonal matrix D such that A = PDP^-1.
Since A is invertible, its inverse A^-1 exists. To show that A^-1 is also diagonalizable, we can consider the inverse of equation A = PDP^-1. Taking the inverse of both sides, we have A^-1 = (PDP^-1)^-1.
By the properties of matrix inverses, we can rewrite this equation as A^-1 = (P^-1)^-1D^-1P^-1. Simplifying further, we get A^-1 = PDP^-1, which is of the same form as the original equation.
Therefore, we have expressed A^-1 as a similarity transformation of the diagonal matrix D using the invertible matrix P. This implies that A^-1 is also diagonalizable.
To learn more about diagonal matrices click here: brainly.com/question/31053015
#SPJ11