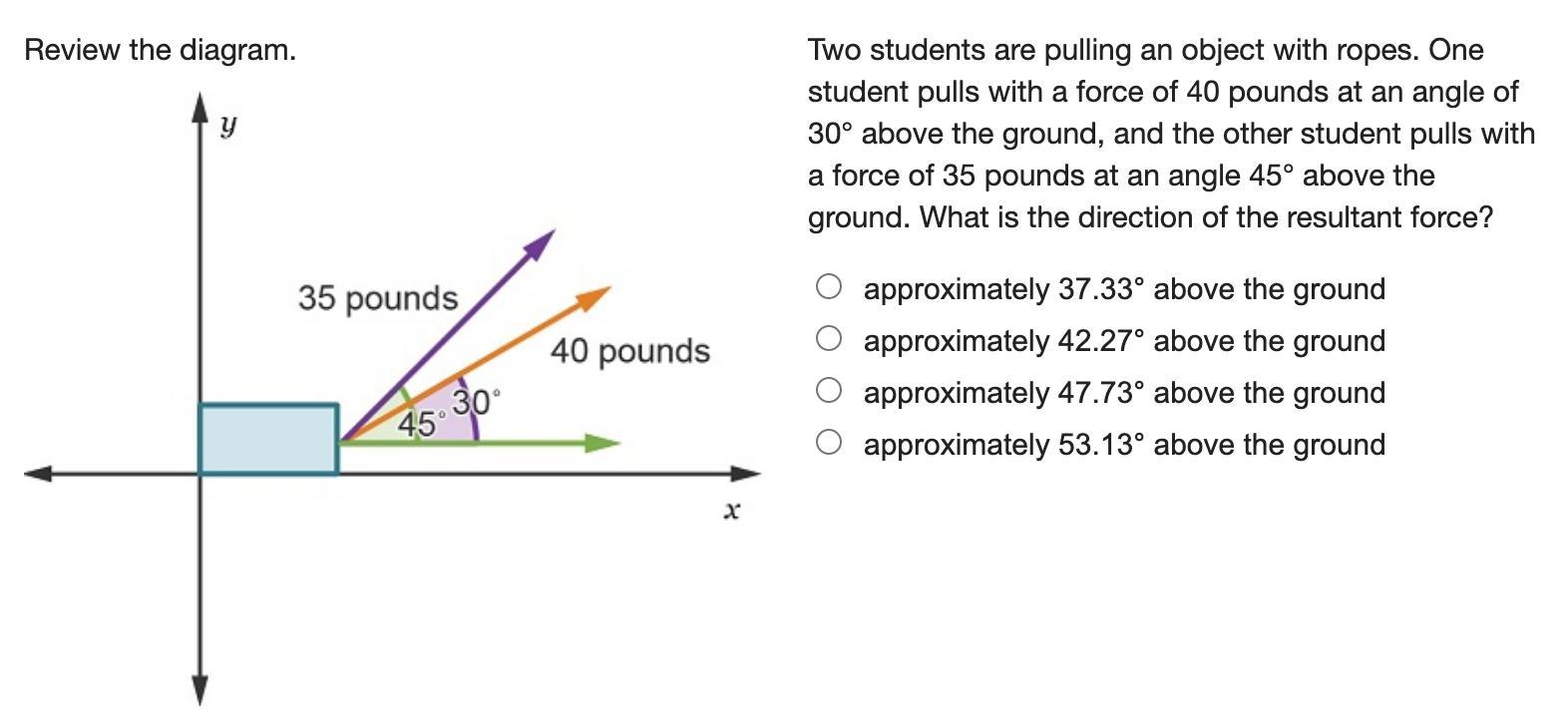
Answers
Answer:
c
Step-by-step explanation:
Just think about the question
c look at the picture carefully
you will understand it more clearly
Related Questions
Help with math problems

Answers
Answer:
1) option A
2) p > 34
Step-by-step explanation:
1) Inequality: 7 ≤ n + 5
Subtract 5 from both sides,
7 - 5 ≤ n +5 - 5
2 ≤ n
The value of n is all values greater than or equal to 2.
So, the answer is option A.
2) Inequality: 16 + p > 50
Solution:
Subtract 16 from both sides,
16 - 16 + p > 50 - 16
p > 34
A house is infested with mice and to combat this the householder acquired four cats cyd, Greg, Ken, and Rom, The householder observes that only half of the creatures caught are mice. A fifth are voles and the rest are birds. 20% of the catches are made by Cyd, 45% by Greg, 10% by Ken and 25% by rom. a) What is the probability of a randomly selected catch being a mouse caught by Cyd? b) Bird not caught by Cyd? c) Greg's catches are equally likely to be a mouse, a bird or a vole. What is the probability of a randomly selected d) The probability of a randomly selected catch being a mouse caught by Ken is 0.05 . What is the probablity that a catch being a mouse caught by Greg? e) Given that the probability of a randomly selected catch is a mouse caught by Rom is 0.2 verify that the catch made by Ken is a mouse? probability of a randomly selected catch being a mouse is 0.5 . f) What is the probability that a catch which is a mouse was made by Cyd?
Answers
Note that the probabilities are given below.
What are the probabilities?
a) the probability of a randomly selected catch being a mouse caught by Cyd
p(Catching a mount) x p(Cyd made the catch)
= 0.5x .2
= 0.1
b) the probability of a bird not caught by Cyd is 0.5 x 0.8 = 0.4.
Thus
P(that a catch is a bird) x p(the Cyd didn't make the catch)
= 0.3 x 0.8
=0.24
c) The probability of a randomly selected catch being caught by Greg is 0.45
To calculate, we say
(0.5 x0.45) + (0.3 x 0.45) + (0.2 x .45)
= 0.45.
d)
P (mouse caught by Greg) = (0.45 x 0.5) / 1
= 0.225.
e) P(catch is a mouse caught by Ken and catch is a mouse)
= P(catch is a mouse | catch is made by Ken) x P(catch is made by Ken)
= 0.05 x 0.1
= 0.005
f)
P (catch made by Cyd | catch is a mouse)
= 0.1 x 0.2 / 0.5
= 0.04
Learn more about probabilities at:
https://brainly.com/question/3003478
#SPJ1
the domain of the function f(x)=50/3x-21 is all real numbers except for
Answers
Answer:
7
Step-by-step explanation:
The denominator cannot be 0, so
\(3x-21 \neq 0 \implies x \neq 7\)
What is the distance from
Point A to point B?

Answers
Distance from A to B = 3 - (-4) = 7
Find the 3rd term in the expansion of ( 5 � − 7 � ) 3 (5x−7y) 3 in simplest form.
Answers
The third term in the expansion of the expression (5x - 7y)³ is 735xy².
Given expression is,
(5x - 7y)³
We have to expand this.
We know that,
(a + b)³ = a³ - 3a²b + 3ab² - b³
Using this,
(5x - 7y)³ = (5x)³ - (3 × (5x)² × 7y) + (3 ×(5x) × (7y)²) - (7y)³
= 125x³ - (3 × 25x² × 7y) + (3 × 5x × 49y²) - 343y³
= 125x³ - 525x²y + 735xy² - 343y³
Here the third term is 735xy².
Hence the third term is 735xy².
Learn more about expansion of expressions here :
https://brainly.com/question/28400521
#SPJ1
Help bc it’s due in a couple hours and im nowhere near done

Answers
Answer: -9 1/4
Step-by-step explanation:
complete the formula to find the area of the triangle plz help I have only 15 mins left

Answers
Explanation:
The height is 3 cm and the base is 4cm.
I believe 5 is there to trick you. The bottom Is always the base and the straight line going vertically is always the height.
1/2*3*4=6
Answer:
6 cm²
Step-by-step explanation:
\(\frac{1}{2}\) × 4 cm × 3 cm = 6 cm²
Hector used the quadratic formula to solve the polynomial equation
9x^2+ 8x - 2 = 0
Which number did Hector have to square when he used the quadratic formula?
Answers
Answer:
STEP
1
:
Equation at the end of step 1
(32x2 - 8x) - 2 = 0
STEP
2
:
Trying to factor by splitting the middle term
2.1 Factoring 9x2-8x-2
The first term is, 9x2 its coefficient is 9 .
The middle term is, -8x its coefficient is -8 .
The last term, "the constant", is -2
Step-1 : Multiply the coefficient of the first term by the constant 9 • -2 = -18
Step-2 : Find two factors of -18 whose sum equals the coefficient of the middle term, which is -8 .
-18 + 1 = -17
-9 + 2 = -7
-6 + 3 = -3
-3 + 6 = 3
-2 + 9 = 7
-1 + 18 = 17
Observation : No two such factors can be found !!
Conclusion : Trinomial can not be factored
Equation at the end of step
2
:
9x2 - 8x - 2 = 0
STEP
3
:
Parabola, Finding the Vertex:
3.1 Find the Vertex of y = 9x2-8x-2
Parabolas have a highest or a lowest point called the Vertex . Our parabola opens up and accordingly has a lowest point (AKA absolute minimum) . We know this even before plotting "y" because the coefficient of the first term, 9 , is positive (greater than zero).
Each parabola has a vertical line of symmetry that passes through its vertex. Because of this symmetry, the line of symmetry would, for example, pass through the midpoint of the two x -intercepts (roots or solutions) of the parabola. That is, if the parabola has indeed two real solutions.
Parabolas can model many real life situations, such as the height above ground, of an object thrown upward, after some period of time. The vertex of the parabola can provide us with information, such as the maximum height that object, thrown upwards, can reach. For this reason we want to be able to find the coordinates of the vertex.
For any parabola,Ax2+Bx+C,the x -coordinate of the vertex is given by -B/(2A) . In our case the x coordinate is 0.4444
Plugging into the parabola formula 0.4444 for x we can calculate the y -coordinate :
y = 9.0 * 0.44 * 0.44 - 8.0 * 0.44 - 2.0
or y = -3.778
Parabola, Graphing Vertex and X-Intercepts :
Root plot for : y = 9x2-8x-2
Axis of Symmetry (dashed) {x}={ 0.44}
Vertex at {x,y} = { 0.44,-3.78}
x -Intercepts (Roots) :
Root 1 at {x,y} = {-0.20, 0.00}
Root 2 at {x,y} = { 1.09, 0.00}
Solve Quadratic Equation by Completing The Square
3.2 Solving 9x2-8x-2 = 0 by Completing The Square .
Divide both sides of the equation by 9 to have 1 as the coefficient of the first term :
x2-(8/9)x-(2/9) = 0
Add 2/9 to both side of the equation :
x2-(8/9)x = 2/9
Now the clever bit: Take the coefficient of x , which is 8/9 , divide by two, giving 4/9 , and finally square it giving 16/81
Add 16/81 to both sides of the equation :
On the right hand side we have :
2/9 + 16/81 The common denominator of the two fractions is 81 Adding (18/81)+(16/81) gives 34/81
So adding to both sides we finally get :
x2-(8/9)x+(16/81) = 34/81
Adding 16/81 has completed the left hand side into a perfect square :
x2-(8/9)x+(16/81) =
(x-(4/9)) • (x-(4/9)) =
(x-(4/9))2
Things which are equal to the same thing are also equal to one another. Since
x2-(8/9)x+(16/81) = 34/81 and
x2-(8/9)x+(16/81) = (x-(4/9))2
then, according to the law of transitivity,
(x-(4/9))2 = 34/81
We'll refer to this Equation as Eq. #3.2.1
The Square Root Principle says that When two things are equal, their square roots are equal.
Note that the square root of
(x-(4/9))2 is
(x-(4/9))2/2 =
(x-(4/9))1 =
x-(4/9)
Now, applying the Square Root Principle to Eq. #3.2.1 we get:
x-(4/9) = √ 34/81
Add 4/9 to both sides to obtain:
x = 4/9 + √ 34/81
Since a square root has two values, one positive and the other negative
x2 - (8/9)x - (2/9) = 0
has two solutions:
x = 4/9 + √ 34/81
or
x = 4/9 - √ 34/81
Note that √ 34/81 can be written as
√ 34 / √ 81 which is √ 34 / 9
Solve Quadratic Equation using the Quadratic Formula
3.3 Solving 9x2-8x-2 = 0 by the Quadratic Formula .
According to the Quadratic Formula, x , the solution for Ax2+Bx+C = 0 , where A, B and C are numbers, often called coefficients, is given by :
- B ± √ B2-4AC
x = ————————
2A
In our case, A = 9
B = -8
C = -2
Accordingly, B2 - 4AC =
64 - (-72) =
136
Applying the quadratic formula :
8 ± √ 136
x = —————
18
Can √ 136 be simplified ?
Yes! The prime factorization of 136 is
2•2•2•17
To be able to remove something from under the radical, there have to be 2 instances of it (because we are taking a square i.e. second root).
√ 136 = √ 2•2•2•17 =
± 2 • √ 34
√ 34 , rounded to 4 decimal digits, is 5.8310
So now we are looking at:
x = ( 8 ± 2 • 5.831 ) / 18
Two real solutions:
x =(8+√136)/18=(4+√ 34 )/9= 1.092
or:
x =(8-√136)/18=(4-√ 34 )/9= -0.203
Two solutions were found :
x =(8-√136)/18=(4-√ 34 )/9= -0.203
x =(8+√136)/18=(4+√ 34 )/9= 1.092
Step-by-step explanation:
Answer:
8
Step-by-step explanation:
ax² + bx + c = 0
In the quadratic formula the "b" coefficent gets sqaured
bx = 8x
b = 8
A snail is at the bottom of a well that is 10 feet deep. Each day he crawls up 3 feet
and each night he slides back 2 feet. How many days will it take him to reach the top
of the well? (HINT: The answer is NOT 10.)
Answers
Answer: 8 days
Step-by-step explanation:
Depth of well = 10
Each day:
Distance crawled up = 3 feets
Distance crawled down = 2feets
Hence ;
Net distance climbed per day:
(distance climbed up - distance crawled down)
= (3 - 2) = 1
If depth of well = 10 and a net distance of 1 feet is claimed daily,
Then after 7 days, the snail would have climbed up to. (7 × 1 feet) = 7 feets
Then on the 8th day, it will crawl a distance of 3 feets upward, hence, position will be (7 + 3) = 10 feets.
Hence, at this point it would have reached the top of the well , and there would be no avenue to crawl downward at night
Hence it will Take 8 days
I have a quick question please someone answer Is 5/8 irrational?
Answers
Answer:
no
Step-by-step explanation:
5/8=0.6250 so its rational
Answer: no
Step-by-step explanation: 5/8 is rational because it is another way of writing the ratio 5:8. So no, 5/8 is not an irrational number.
Cousteau is building a cubed cage for a parrot at his local zoo. Since the the cage's side length is 12 feet, its volume will be 12³ cubic feet. Can you help Cousteau write out 12³ in expanded form?
Answers
The expanded form of 12³ is given as follows:
12³ = 12 x 12 x 12 = 1728 cubic feet.
How to obtain the volume of a cube?The volume of a cube of side length a is given by the cube of the side length, as follows:
V(a) = a³.
This expression is equivalent to multiplying the side length of the object by itself twice, as follows:
V(a) = a x a x a.
The side length for this problem is given as follows:
a = 12 feet.
Hence the volume of the cube is given as follows:
V = 12³ = 1728 feet³.
More can be learned about the volume of a cube at https://brainly.com/question/1972490
#SPJ1
The length of a rectangle is 8 inches longer than 3 times its width. The area of the rectangle is 156 square inches.
What is the width of the rectangle?
Answers
The Answer:
Width = 6
Step-by-step explanation:
Let width be w
(3w + 8) x w = 156
3 \(w^{2}\) x 8n - 156 = 0
(w + 8 x 6) (w-6) = 0
w = 6
If H be the H.M. between a and b.
prove that 1/H-a + 1/H-b = 1/a+1/b
Answers
if susjwmaoakkaajKIJahabsbzh
A small box measures 7 in. by 10 in. by
3/4 in. high. Find the volume of the box.
Answers
Answer:
Volume = 52.5
Step-by-step explanation:
volume of a rectangular 3d shape can be calculated by length*width*height. In this case:
7*10*0.75 = 52.5
Point A and point B are placed on a number line. Point A is located at -5 and point B is 10 less than point A. Which statement about point B is true?
Answers
Given :
Point A and point B are placed on a number line.
Point A is located at -5 and point B is 10 less than point A.
To Find :
Position of point B in number line.
Solution :
It is given that position of point A is -5 on number line.
So, value of A is -5.
Now, it is given that point B is 10 less than point A.
B = [ -5 + ( -10 ) ] = -15
Therefore, position of point B is [ -5 + ( -10 ) ] = -15 .
The cost, c(x), for a taxi ride is given by c(x) = 3x + 2.00, where x is the
number of minutes.
On a piece of paper, graph c(x) = 3x + 2.00. Then determine which answer matches the graph you drew, including the correct axis labels,

Answers
Answer:
Graph D is the correct answer
Step-by-step explanation:
The graph of is attached.
The y-axis of the graph represents the cost, and the x-axis represents the number of minutes.
Also, the slope of is 2, and the y-intercept is 2.
Now let us look at the choices given and determine which graph represents the function .
The first graph has the slope of 2, and a y-intercept of 2, but the y-axis represents minutes, and the x-axis represents cost—this does not match our graph.
The second graph has y-intercept of 3—also not our graph.
The third graph also has a y-intercept of 3—this does match our graph either.
The fourth graph has a y-intercept of 2 and a slope of 2, and its y-axis represents the cost and x-axis represents the minutes—this perfectly matches our graph.
Therefore, the graph that matches our graph is D.
The diameter of a cone is 34 ft. the height is 16 ft what is the volume in cubic ft?
Answers
Answer:
4842.24 cubic feet
Step-by-step explanation:
Use the formula for the volume of a cone, V = \(\pi\)r²\(\frac{h}{3}\)
The diameter of the cone is 34 ft, so the radius is 17 ft.
Plug in the radius and height into the formula, and solve for the volume:
V = \(\pi\)r²\(\frac{h}{3}\)
V = \(\pi\)(17)²\(\frac{16}{3}\)
V = \(\pi\)(289)\(\frac{16}{3}\)
V = 4842.24
So, the volume of the cone is 4842.24 cubic feet
Answer:
4,841.32 ft³.
Step-by-step explanation:
Let’s assume that this is a right circular cone and that the radius of the cone is r.
For our problem, r = (1/2)d = (1/2)34 = 17.
The volume of the cone is:
V = (1/3)pi r^2 h, where r is the radius and h is the height.
So, V = (1/3)pi(17^2)16 = 4,841.32 ft³.
Which is cheaper: eating out or dining in? The mean cost of a flank steak, broccoli, and rice bought at the grocery store is $13.04. A sample of 100 neighborhood restaurants showed a mean price of $12.60 and a standard deviation of $2 for a comparable restaurant meal. (a) Choose the appropriate hypotheses for a test to determine whether the sample data support the conclusion that the mean cost of a restaurant meal is less than fixing a comparable meal at home. H0: - Select your answer - Ha: - Select your answer - (b) Using the sample from the 100 restaurants, what is the p value? If required, round your answer to four decimal places. (c) At α = 0.05, what is your conclusion? We - Select your answer - the null hypothesis. We - Select your answer - conclude that the cost of a restaurant meal is significantly cheaper than a comparable meal fixed at home.
Answers
Answer:
a) The null and alternative hypothesis are:
\(H_0: \mu=13.04\\\\H_a:\mu< 13.04\)
b) P-value = 0.0151
c) We reject the null hypothesis.
We conclude that the cost of a restaurant meal is significantly cheaper than a comparable meal fixed at home.
Step-by-step explanation:
This is a hypothesis test for the population mean.
The claim is that the mean cost of a restaurant meal is significantly less than fixing a comparable meal at home.
Then, the null and alternative hypothesis are:
\(H_0: \mu=13.04\\\\H_a:\mu< 13.04\)
The significance level is 0.05.
The sample has a size n=100.
The sample mean is M=12.6.
As the standard deviation of the population is not known, we estimate it with the sample standard deviation, that has a value of s=2.
The estimated standard error of the mean is computed using the formula:
\(s_M=\dfrac{s}{\sqrt{n}}=\dfrac{2}{\sqrt{100}}=0.2\)
Then, we can calculate the t-statistic as:
\(t=\dfrac{M-\mu}{s/\sqrt{n}}=\dfrac{12.6-13.04}{0.2}=\dfrac{-0.44}{0.2}=-2.2\)
The degrees of freedom for this sample size are:
\(df=n-1=100-1=99\)
This test is a left-tailed test, with 99 degrees of freedom and t=-2.2, so the P-value for this test is calculated as (using a t-table):
\(\text{P-value}=P(t<-2.2)=0.0151\\\)
As the P-value (0.0151) is smaller than the significance level (0.05), the effect is significant.
The null hypothesis is rejected.
There is enough evidence to support the claim that the mean cost of a restaurant meal is significantly less than fixing a comparable meal at home.
There is enough evidence to support the claim that the mean cost of a restaurant meal is significantly less than fixing a comparable meal at home.
The hypothesesThe null hypothesis is always represented by the equality sign.
So, the null hypothesis is:
\(H_o : \mu = 13.04\)
For the meal to be cheaper, then the less than inequality sign would be used.
So, the alternate hypothesis is:
\(H_a : \mu < 13.04\)
Hence, the null and the alternate hypotheses are:
\(H_o : \mu = 13.04\) and \(H_a : \mu < 13.04\)
The p value for a sample size of 100The given parameters are:
n = 100
\(\sigma = 2\)
\(\bar x = 13.04\)
\(\mu = 12.60\)
Start by calculating the standard error
\(\sigma_x = \frac{\sigma}{\sqrt n}\)
This gives
\(\sigma_x = \frac{2}{\sqrt {100}}\)
\(\sigma_x = 0.2\)
Next, calculate the test statistic
\(t = \frac{\mu - \bar x}{\sigma_x}\)
This gives
\(t = \frac{12.60 - 13.04}{0.2}\)
\(t = -2.2\)
Calculate the degrees of freedom
\(df = n - 1\)
\(df = 100 - 1\)
\(df = 99\)
Next, we calculate the p-value as follows:
\(p = P(t < -2.2)\)
At a degree of freedom of 99, the p value when the t value is less than -2.2 is:
\(p = 0.0151\)
Hence, the p value for a sample size of 100
The conclusionWe have:
The significance level, α = 0.05
The p-value in b, 0.0151 is lesser than the significance level, 0.05.
This means that we reject the null hypothesis
So, the conclusion is:
There is enough evidence to support the claim that the mean cost of a restaurant meal is significantly less than fixing a comparable meal at home.
Read more about hypothesis testing at:
https://brainly.com/question/15980493
Hurry I am timed Which tiny, round “factory” puts together protein and is often found in the endoplasmic reticulum?
ribosome
chromosome
Golgi body
chloroplast
Answers
Answer:
the answer is ribsome
The ribosome serves as the site and carries the enzymes necessary for protein synthesis. They are often takes the shape of small round particles attached in the endoplasmic reticulum.
A single die is rolled. Find the odds in favor of rolling a number greater than 2.
The odds in favor of rolling a number greater than 2 are
(Simplify your answers.)
Answers
Answer:
2/3
Step-by-step explanation:
1 and 2 are taken away, therefore you have 3, 4, 5, and 6 left as options to roll. So the answer is 4/6 since there's 4 numbers, but simplified it's 2/3.
Answer:
There are six possible outcomes when rolling a die, each of which is equally likely. Of these six outcomes, three are greater than 2 (3, 4, 5) and three are not (1, 2, 6). Therefore, the odds in favor of rolling a number greater than 2 are 3 to 3, or simply 1 to 1. Alternatively, we could express this as a probability: the probability of rolling a number greater than 2 is 3/6, or 1/2, since there are three favorable outcomes out of a total of six possible outcomes.
Step-by-step explanation:
Peter says If you subtract 18 from my number and multiply the difference by -6 , the result is -126." What is Peter's number?
Answers
Explanation
Let x= peters number
Subtract 18 from #: x-18
Multiply the difference by -6: -6(x-18)
Results is: -126
—-> -6(x-18) =-126
Then solve for x.
Distribution: -6x + 108 = -126
Subtract-126 on both sides: -6x = -234
Divide-6: x= 39
how do you slove a quadratic function by factoring?
Answers
Answer: Answer is below <3
Step-by-step explanation:
1 . Transform the equation using standard form in which one side is zero.
2 . Factor the non-zero side.
3 . Set each factor to zero (Remember: a product of factors is zero if and only if one or more of the factors is zero).
4 . Solve each resulting equation.
A culture started with 3000 becteria. after 8 hours it grew to 3300 becteria. Predict how many bacteria will be present after 12 hours. Round your answer to the nearest whole number. p=ae^kt
Answers
Answer: I think 5000
Step-by-step explanation:
I’m probably completely wrong lol sorry
Which equations support the fact that rational numbers are closed under addition? Select each correct answer.
A) √2+(−√6)=0
B) √2 + √2 = 2√2
C) 1/3 + 1/3 = 2/3
D) √9 + √9 = 2√9
Answers
The options that supports that rational numbers are close under addition are:
C) 1/3 + 1/3 = 2/3D) √9 + √9 = 2√9What does it mean rational number are close under addition ?Firstly we define rational numbers as numbers that can form a fraction consisting of integers excluding zero.
Rational numbers are close under addition that means that addition of two rational numbers will not create a irrational number
The given problem
adding the fraction 1/3 + 1/3 = 2/3
all the numbers involved here are rational numbers
√9 + √9 = 2√9
√9 is a rational number since √9 = 3.
2√9 is also a rational number
√2 and √6 are irrational numbers.
Learn more on Rational numbers are close under addition:
https://brainly.com/question/7264771
#SPJ1
Find the length of BC

Answers
bc=√{ac²-ab²}
bc=√{16²-11²}
bc=√{256-121}
bc=√{135}
bc=11.62
Let Q be an orthogonal matrix with an eigenvalue λ1=1. Let x be an eighenvector beloinging to λ1. Show that x is also an eigenvector of QT
Answers
If Q is an orthogonal matrix with an eigenvalue λ1 = 1, then x, the eigenvector corresponding to λ1, is also an eigenvector of QT with an eigenvalue λ2 = λ1 * (QT * x).
To show that x is also an eigenvector of QT, we need to demonstrate that QT * x is a scalar multiple of x.
Given that Q is an orthogonal matrix, we know that QT * Q = I, where I is the identity matrix. This implies that Q * QT = I as well.
Let's denote x as the eigenvector corresponding to the eigenvalue λ1 This means that Q * x = λ1 * x.
Now, let's consider QT * x. We can multiply both sides of the equation Q * x = λ1 * x by QT:
QT * (Q * x) = QT * (λ1 * x)
Applying the associative property of matrix multiplication, we have:
(QT * Q) * x = λ1 * (QT * x)
Using the fact that Q * QT = I, we can simplify further:
I * x = λ1 * (QT * x)
Since I * x equals x, we have:
x = λ1 * (QT * x)
Now, notice that λ1 * (QT * x) is a scalar multiple of x, where the scalar is λ1. Therefore, we can rewrite the equation as:
x = λ2 * x
where λ2 = λ1 * (QT * x).
This shows that x is indeed an eigenvector of QT, with the eigenvalue λ2 = λ1 * (QT * x).
In conclusion, if Q is an orthogonal matrix with an eigenvalue λ1 = 1, then x, the eigenvector corresponding to λ1, is also an eigenvector of QT with an eigenvalue λ2 = λ1 * (QT * x).
for more such question on matrix visit
https://brainly.com/question/2456804
#SPJ8
HELP DUE LATER TODAY:The temperature outside dropped 13°F in 6 hours. The final temperature was -4°F. What
was the starting temperature?
Answers
Answer:the answer is 9
Step-by-step
If you subtract 13 by 4 it’s 9
A store is selling 5 cans of tomato sauce for 4.50 what is the unit price
Answers
Answer:All you have is multiply
4.50/5 = 0.9
The unit price is 0.9
Step-by-step explanation: I did it and got it right
HELLLLPPPPP MEEE PLEASEEE I NEED A GOOD GRADE

Answers
Answer: x=11
Step-by-step explanation:
4x+4x+2=90
8x+2=90
8x=88
x=11
There are 5 blue birds, 6 green ones and 3 black ones. If I randomly catch 2 birds, what is the probability the first bird is black and the second is green?
Answers
Answer:
So you must first get the total of all the birds, which is going be a fraction of course , that being 14/14 birds in total, since there are only 3 black birds the probability of me getting a black one 3/14 because there are fourteen in total, and the probability for the green birds is 6/14.
The combined probability that the first bird is black and the second is green is 0.0918
What is Probability?Probability is the likeliness of an event to happen.
Total Blue birds = 5
Total Green birds = 6
Total Black birds = 3
Total birds = 14
The probability of selecting two birds such that the first bird is black and the second is green.
Probability = ( No. of the desired outcome )/( Total outcomes)
The probability of selecting black bird is 3/14
The probability of selecting green bird is 6/14
Therefore, the combined probability that the first bird is black and the second is green is
= (3/14) * (6/14)
= 18/196
= 0.0918
To know more about Probability
https://brainly.com/question/11234923
#SPJ2