Will give brainliest, like, comment and 5 points for the best answer
Could you please help me with this question:

Answers
Answer:
$1.80, $2.90, $4.00, $10.90
Step-by-step explanation:
For 9/10 mile, the price will be $1.80. For 2 miles, the price will be $2.90. For 3 1/10 miles, the price will be $4.00, and for 10 miles, the price will be $10.90. The relationship between distance travelled and the price is not proportional because it costs $1.00 for the first 1/10 mile and then for every additional 1/10 mile, it only costs $0.10. Hope it helps!
Related Questions
help me plz due today

Answers
x = 21
The area of a circle of radius 1 is π units squared. Use scaling to explain why the area of a circle of radius r is πr^2 units squared
Answers
The area of the circle with radius 'r' is πr² units² because the formula for the area of a circle = πr²
How to calculate the area of a circle?The circle is defined as a closed two-dimensional figure in which the set of all the points in the plane is equidistant from a given point which is the centre.
The angle at the center of a circle sums up to 360°.
To calculate the area of a circle, the formula that should be used is given as follows;
Area of a circle = πr²
radius of the circle = r units
area = π×r ×r
= πr² units ²
Learn more about area here:
https://brainly.com/question/28470545
#SPJ1
A car rental agency charges $15 a day for driving a car 200 miles or less. If a car is driven over 200 miles, the renter must pay $0.05 for each mile over 200 driven. Which of the following functions represents the cost to drive a car from this agency miles x a day?

Answers
The function which represents the cost to drive a car from this agency miles x a day is :
C(x) = 15, if 0 ≤ x ≤ 200
= 15 + 0.05x, if x > 200
Given that,
A car rental agency charges $15 a day for driving a car 200 miles or less.
The function can be written as,
C(x) = 15 if 0 ≤ x ≤ 200
If a car is driven over 200 miles, the renter must pay $0.05 for each mile over 200 driven.
C(x) = 15 + 0.05x, if x > 200
Hence the correct option is D.
Learn more about Functions here :
https://brainly.com/question/29067911
#SPJ1
PLZ HELP I WILL GIVE BRAINLIEST

Answers
Answer:
the third one
Step-by-step explanation:
bc like there are 2 boxes of 1 and 5 boxes of 1/6 so thats already 2 and 5/6 which applies to all of them. then there is 1 box of 1 and 2 boxes of 1/3 so thats 1 and 1/3 which applies to all of them also but when you make them have the same denominator you get 2 and 5/6 + 1 and 4/6 which deletes the second one. When you add you should get the same denominator so that deletes the first one so then you simplify that and the fraction should still be equal to the unsimplified fraction so you should get 4 and 1/2 if that makes sense
in a class of 18 students there are 11 math majors and 7 computer science majors. four students are randomly picked to prepare a demonstration on the use of a graphing calculator
Answers
The probability that 2 math majors and 2 computer science majors are chosen is 0.3778.
In a class of 18 students, there are 11 math majors and 7 computer science majors. Four students are randomly picked to prepare a demonstration on the use of a graphing calculator. Then the probability that 2 math majors and 2 computer science majors are chosen To solve the problem, we need to use combinations as the order in which the students are selected doesn't matter.
The total number of ways of choosing 4 students out of 18 students is shown by :18C4 = (18 × 17 × 16 × 15) / (4 × 3 × 2 × 1) = 3060 The number of ways of choosing 2 math majors from 11 math majors is shown by :11C2 = (11 × 10) / (2 × 1) = 55 .The number of ways of choosing 2 computer science majors from 7 computer science majors is given by :7C2 = (7 × 6) / (2 × 1) = 21 Thus, the number of ways of choosing 2 math majors and 2 computer science majors out of 11 math majors and 7 computer science majors, respectively, is given by :55 × 21 = 1155 Therefore, the probability that 2 math majors and 2 computer science majors are chosen is :1155 / 3060 = 0.3778 (rounded to four decimal places)Thus, the probability that 2 math majors and 2 computer science majors are chosen is 0.3778.
To know more about graphing calculator visit:
https://brainly.in/question/54275321
#SPJ11
3060 possible groups of four students can be formed using a combination of math majors and computer science majors.
In a class of 18 students there are 11 math majors and 7 computer science majors. Four students are randomly picked to prepare a demonstration on the use of a graphing calculator.
We need to find out how many possible groups of four students can be formed using a combination of math majors and computer science majors.
We can apply the combination formula to find the number of possible combinations.
The combination formula is given as: C(n, r) = (n!)/(r!(n-r)!) Where, n is the total number of items available for selection, r is the number of items to be selected at a time C(n, r) is the number of possible combinations.
The number of math majors = 11
The number of computer science majors = 7
The total number of students = 18
We need to select a group of four students, therefore r = 4
The number of possible groups of four students can be formed using a combination of math majors and computer science majors is given by: C(18, 4) = (18!)/(4!(18-4)!)= (18 × 17 × 16 × 15)/(4 × 3 × 2 × 1) = 3060
Therefore, there are 3060 possible groups of four students that can be formed using a combination of math majors and computer science majors.
To know more about combinations:
https://brainly.in/question/16779580
#SPJ11
k^4/(16k^6 5) use the comparison test or limit comparison test to determine whether the following series converges.
Answers
To use the comparison test or limit comparison test, we need to find a known series that either diverges or converges and is similar to the given series.
Using the comparison test, we can compare the given series to the series 1/n^2, which is a p-series with p=2 and converges.
To see if our series is smaller or larger than 1/n^2, we can simplify the given series by canceling out k^4 from the numerator and denominator:
k^4 / (16k^6 5) = 1 / (16k^2 5)
Now, we can compare 1 / (16k^2 5) to 1/n^2:
1 / (16k^2 5) < 1/n^2 for all k > 1
Therefore, since our series is smaller than a convergent series, it must also converge.
Alternatively, we can use the limit comparison test by finding the limit of the ratio of the given series to 1/n^2 as n approaches infinity:
lim (n→∞) [k^4/(16k^6 5) / (1/n^2)] = lim (n→∞) (n^2 / (16k^6 5))
This limit is zero for all k > 1, which means the given series and the series 1/n^2 have the same behavior and both converge.
Learn more about converges here:
https://brainly.com/question/29258536
#SPJ11
A pot of boiling water with a temperature of 100°C is set in a room with a temperature of 20°C. The temperature T of the water after x hours is given by T(x) 20 80 e X. (a) Estimate the temperature of the water after 4 hours. (b) How long did it take the water to cool to 50°C? After 4 hours, the tempertaure of the water will be approximately°C. (Type an integer or decimal rounded to one decimal place as needed.) hour(s) The water will cool to 50°C in about (Type an integer or decimal rounded to two decimal places as needed.)
Answers
The water takes approximately 1.080 hours (or about 1 hour and 4 minutes) to cool to 50°C.
(a) To estimate the temperature of the water after 4 hours, we can substitute x = 4 into the given equation T(x) = 20 + 80e^x.
T(4) = 20 + 80e^4 ≈ 20 + 80(54.6) ≈ 20 + 4368 = 4388°C.
Therefore, the estimated temperature of the water after 4 hours is approximately 4388°C.
(b) We need to find the time it takes for the temperature of the water to cool to 50°C. To do this, we set T(x) = 50 and solve for x.
50 = 20 + 80e^x
Subtracting 20 from both sides:
30 = 80e^x
Dividing both sides by 80:
0.375 = e^x
To solve for x, we take the natural logarithm of both sides:
ln(0.375) = ln(e^x)
Using the property of logarithms, ln(e^x) = x:
x = ln(0.375)
Using a calculator, we find:
x ≈ -1.080
Since time cannot be negative in this context, we discard the negative value.
Learn more about logarithm at: brainly.com/question/30226560
#SPJ11
I think the my dogs is 12 pound and my cat has 3 times has many pounds as my dogs (explain how you got your answer)
Answers
Answer:
The weight of the dog = 12 Pounds.
The weight of the cat = 3× Of dogs weight.
= 3×12 = 36 Pounds.
Therefore cat is 36 Pounds.
Gerry wants to construct a triangle with segments that are 4, 6, and 11 inches long. Is his triangle possible? Explain how you know.
Answers
Answer:
No, this triangle is not possible
Step-by-step explanation:
By the Triangle Inequality Theorem, it should be that:
a + b > c,
a + c > b, ⇒ a, b, and c are sides of this triangle
b + c > a
~ In this case let us say a = 4 inches, b = 6 inches, and c = 11 inches ~
4 + 6 > 11,
4 + 11 > 6, ⇒ Here 10 is not greater than 3rd side and thus
11 + 6 > 4 doesn't form a triangle
The length of the sides of a triangle are y, y + and 7 centimeters. If the triangles perimeter is 56 centimeters, what is the value of y?
A) 24
B) 25
C)31
D) 32
Answers
(20 points) Find the orthogonal projection of
v⃗ =⎡⎣⎢⎢⎢0003⎤⎦⎥⎥⎥v→=[0003]
onto the subspace WW of R4R4 spanned by
⎡⎣⎢⎢⎢−1−1−1−1⎤⎦⎥⎥⎥, ⎡⎣⎢⎢�
Answers
The orthogonal projection of v⃗ onto the subspace W of R4 spanned by [-1, -1, -1, -1] and [2, 2, 2, 2] is [-0.5, -0.5, -0.5, -0.5].
How will ufind the orthogonal projection of v⃗ onto the subspace W?To find the orthogonal projection of v⃗ onto the subspace W, we need to project v⃗ onto each of the basis vectors of W and then sum them up. The projection of v⃗ onto a vector u⃗ is given by the formula proju⃗(v⃗) = (v⃗ · u⃗) / ||u⃗||^2 * u⃗, where · denotes the dot product.
First, we calculate the projection of v⃗ onto the first basis vector [-1, -1, -1, -1]:
proj-1, -1, -1, -1 = (v⃗ · [-1, -1, -1, -1]) / ||[-1, -1, -1, -1]||^2 * [-1, -1, -1, -1]
= (0 * -1 + 0 * -1 + 0 * -1 + 3 * -1) / (1 + 1 + 1 + 1) * [-1, -1, -1, -1]
= (-3) / 4 * [-1, -1, -1, -1]
= [-0.75, -0.75, -0.75, -0.75]
Next, we calculate the projection of v⃗ onto the second basis vector [2, 2, 2, 2]:
proj2, 2, 2, 2 = (v⃗ · [2, 2, 2, 2]) / ||[2, 2, 2, 2]||^2 * [2, 2, 2, 2]
= (0 * 2 + 0 * 2 + 0 * 2 + 3 * 2) / (4 + 4 + 4 + 4) * [2, 2, 2, 2]
= 6 / 16 * [2, 2, 2, 2]
= [0.375, 0.375, 0.375, 0.375]
Finally, we add up the two projections:
[-0.75, -0.75, -0.75, -0.75] + [0.375, 0.375, 0.375, 0.375] = [-0.375, -0.375, -0.375, -0.375]
Therefore, the orthogonal projection of v⃗ onto the subspace W is [-0.375, -0.375, -0.375, -0.375].
Learn more about orthogonal projections
brainly.com/question/27749918
#SJP11
F is the mid point of EG . If EF = 5x and EG = 7x + 5, what is EG?
Answers
A researcher records the hospital admission rates for coronary heart disease at 10 local hospitals. She finds that two different hospitals had the highest overall rates of hospital admissions. Which measure of central tendency did this researcher use to describe these data
Answers
The researcher most likely used the mean as the measure of central tendency to describe,
the hospital admission rates for coronary heart disease at the 10 local hospitals. The mean is calculated by adding up all of the hospital admission rates and dividing by the total number of hospitals.
By identifying the two hospitals with the highest overall rates of hospital admissions, the researcher likely calculated the mean of all the hospital admission rates and compared each hospital's rate to this value.
This helps to identify which hospitals had rates that were higher or lower than average.
However, without more information on the data distribution, it is possible that the researcher could have also used the median or mode as the measure of central tendency.
Learn more about data here:brainly.com/question/29122373
#SPJ11
find the value of each variable angle a, angle b, angle c, and angle d outside of a circle is 43 degrees
Answers
Without any additional information about the intercepted arcs or the relationship between the angles, we cannot determine their exact values.
Given that angle d outside of a circle is 43 degrees, we can use the following properties of angles in circles to find the values of angle a, angle b, and angle c:
1. Inscribed Angle: The measure of an inscribed angle is half the measure of its intercepted arc.
2. Central Angle: The measure of a central angle is equal to the measure of its intercepted arc.
3. External Angle: The measure of an external angle is half the difference between the measures of its intercepted arcs.
Using these properties, we can find the value of angle a, angle b, and angle c. However, Please provide more information about the angles' relationships or the intercepted arcs.
To learn more about : values
https://brainly.com/question/843074
#SPJ11
fill in the missing values in the table below

Answers
The missing values on the table are given as follows:
D. 4, 80%.
How to calculate a probability?A probability is calculated as the division of the desired number of outcomes by the total number of outcomes in the context of a problem/experiment.
One of the five outcomes represent a one, hence the outcomes that do not represent a one is given as follows:
5 - 1 = 4.
Hence the probability is given as follows:
p = 4/5 x 100%
p = 80%.
More can be learned about probability at https://brainly.com/question/24756209
#SPJ1
6. Joshua took a bus from Orlando to Atlanta. The bus traveled 420 miles in 6 hours. What was the
average speed of the bus?
a) 60 miles per hour
b) 65 miles per hour
c) 70 miles per hour
d) 75 miles per hour
Answers
assume that the traffic to the web site of made by charmz, llc which sells customized mugs, follows a normal distribution, with a mean of 8.5 million visitors per day and a standard deviation of 610,000 visitors per day. what is the probability that the web site has fewer than 8 million visitors in a single day?
Answers
The probability that the website has fewer than 8 million visitors in a single day is 0.2061 or 20.61%.Hence, option C is correct.
The traffic to the web site of Made by Charmz, LLC which sells customized mugs, follows a normal distribution,
with a mean of 8.5 million visitors per day and a standard deviation of 610,000 visitors per day.
The problem asks us to find the probability that the website has fewer than 8 million visitors in a single day.
Therefore, we need to find P(X < 8 million).
Using the Z-score formula, we have;
\(Z=\frac{X-\mu}{\sigma}\)
Where X = 8 million, μ = 8.5 million and σ = 610,000.
Substituting the given values in the formula, we get:
\(Z=\frac{8-8.5}{0.61}=-0.8197\)
Using a standard normal table, the probability corresponding to Z-score = -0.8197 is 0.2061.
Therefore, the probability that the website has fewer than 8 million visitors in a single day is 0.2061 or 20.61%.Hence, option C is correct.
for such more question on probability
https://brainly.com/question/13604758
#SPJ11
The population of a county increases at a rate proportional to the existing population. If the population doubles in 20 years, then find the factor (constant) of proportionality, k. __________________________________________________________________________________________________________________________________________________________________________________________________________
Answers
Answer:
The constant factor of proportionality is k=ln2/20=0.034657 (approx)
k=0.034657 (approx)
Let P(t) be the population of a county after t years.
The population of a country increases at a rate proportional to the existing population.
Mathematically, it can be represented as
dP/dt=kP
where k is a constant factor of proportionality.
To find k, we need to solve the differential equation.
dP/dt=kP
By separation of variables, we get
∫dP/P=∫kdt
On integrating both sides, we get
ln|P|=kt+C
Where C is the constant of integration.
Raising e to both sides, we get
|P|=e^(kt+C)=e^C.e^(kt)
Taking e^C as a constant A, we get
|P|=A.e^(kt) ------(1)
Given that population doubles in 20 years.
It means P(20)=2P(0)
Substituting the values in equation (1), we get
2P(0)=A.e^(k×20) ------(2)
Again, given that population doubles in 20 years.
It means P(40)=2P(20) = 2×2P(0) = 4P(0)
Substituting the values in equation (1), we get
4P(0)=A.e^(k×40) ------(3)
Dividing equation (3) by equation (2), we get
4P(0)/2P(0)=A.e^(k×40)/A.e^(k×20)2
=e^(k×20)
Taking natural log of both sides, we get
ln2=k×20
k=ln2/20
Therefore, the constant factor of proportionality is k=ln2/20=0.034657 (approx)
Answer: k=0.034657 (approx)
Learn more about proportionality, visit here:
https://brainly.in/question/22055811
#SPJ11
Mrs Mabaspacked , prudence's mom packed a cooler box bag for the day of the painting . Two six pack cans fit exactly on top of each other in the cooler bag. A can has a diameter of 6 cm and a height of 8,84 cm 0:41 EZ07/67/90 dy the information given in the information above and answer the questions that follow. 2.1 2.2 2.3 2.4 Calculate the volume in ml of one can of cold drink, rounded to the nearest whole number. Determine the height of the cooler bag, rounded to the nearest whole number. Determine the volume in ml of the cooler bag if the breadth of the bag is 12 cm and the length 18 cm. Each can have a label on them as shown by the image below Piesse Circumference of the can NEW Diet, Soda 0 Calories! Calculate the length of the lable. CALORIES PER SERVING Nutrition Fac Hight of the can (3) (2) (3) (2) 27 [10]
Answers
2.1 The volume in ml of one can of cold drink is 83 ml.
2.2 The height of the cooler bag is 18 cm.
2.3 The volume in ml of the cooler bag if the breadth of the bag is 12 cm and the length 18 cm is 3,888 ml.
2.4 The circumference of the can is 18.84 cm.
How to calculate the volume of a cylindrical can?In Mathematics and Geometry, the volume of a cylinder can be calculated by using this formula:
Volume of a cylinder, V = πr²h
Where:
V represents the volume of a cylinder.h represents the height or length of a cylinder.r represents the radius of a cylinder.By substituting the given side lengths into the volume of a cylinder formula, we have the following;
Volume of can = 3.14 × (6/2)² × 8.84
Volume of can = 83.27 cm³.
Note: 1 cm³ = 1 ml
Volume of can in ml = 83.27 ≈ 83 ml.
Part 2.2.
For the height of the cooler bag, we have:
Height of cooler bag = 2 × height of can
Height of cooler bag = 2 × 8.84
Height of cooler bag = 17.68 ≈ 18 cm.
Part 2.3
Volume of cooler bag = length × breadth × height
Volume of cooler bag = 18 × 12 × 18
Volume of cooler bag = 3,888 ml.
Part 2.4
The circumference of the can is given by:
Circumference of circle = 2πr
Circumference of can = 2 × 3.14 × 3
Circumference of can = 18.84 cm.
Read more on cylinder here: brainly.com/question/14060443
#SPJ1
Missing information:
The question is incomplete and the complete question is shown in the attached picture.

Find the exact value of the area between the graphs of y = cos x and y = e x for 0 ≤ x ≤ 1.
Both graphs start at y = 1 when x = 0, and then the exponential graph goes above the
cosine graph. Therefore, the area we are looking for is defined by the integral of (upper
function) - (lower function):
Answers
The exact value of the area between the graphs y = cos x and y = eˣ is 0.877.
What is Integration?Integration is the process reverse to differentiation. It is a method of adding the parts to get the whole.
The exponential graph goes above the cosine graph. Therefore, the area we are looking for is the difference of the area formed by the exponential graph and the area formed by the cosine graph.
Let A be the required area.
Let A₁ be the area of the graph formed by the cosine function. Then this area is the integral of the cosine function from the limit 0 to 1.
A₁ = \(\int\limits^1_0 {cos x} \, dx\)
= [sin x]¹₀
Giving the values of the limits, we get
A₁ = sin 1 - sin 0
Now, the value of sin 0 equals 0.
A₁ = sin 1
Let A₂ be the area formed by the graph of exponential function.
A₂ = \(\int\limits^1_0 {e^x} \, dx\)
= [eˣ]¹₀
= e¹ - e⁰
= e - 1 ( Since any value raise to 0 equals 1, e⁰ = 1.
Now, A = A₂ - A₁
= e - 1 - sin 1
Value of e equals 2.718 and value of sin 1 equals 0.841
A = 2.718 - 1 - 0.841 = 0.877
Hence the exact value of the area between the graphs y = cos x and y = eˣ is 0.877.
To learn more about Integrals, click:
https://brainly.com/question/18125359
#SPJ1
5.
Which picture shows a rotation of the flag?
(1)
(2)
(3)
(4)
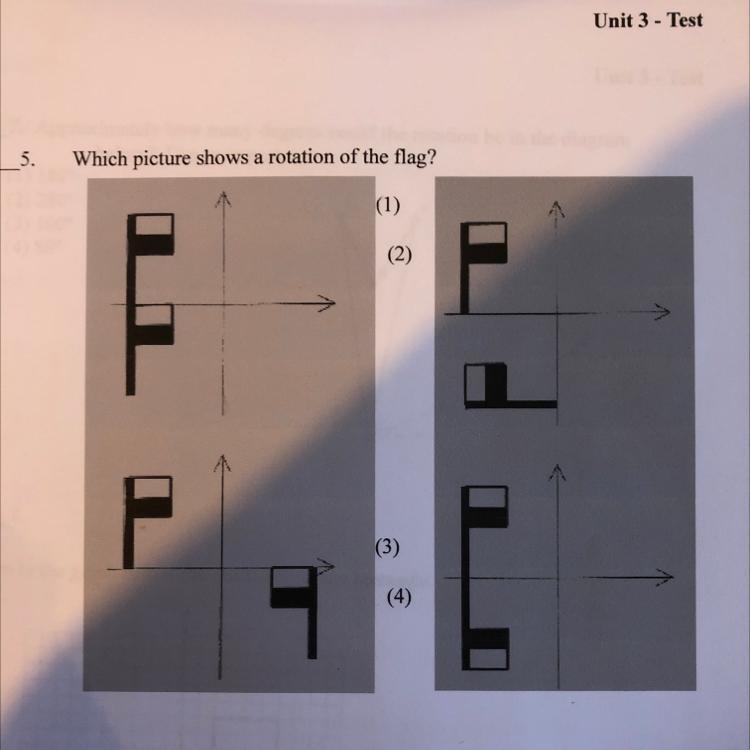
Answers
Answer:
4 my good sir
Step-by-step explanation:
The manager wants to control the maximum probability of Type I error at 1% (i.e. the manager wants the significance level to be 1%). Calculate the critical value the manager should use to conduct the hypothesis test of interest. The null hypothesis is that mean daily output is no greater than 200, and the alternative hypothesis that it is greater than 200. Continue to assume that daily output levels are approximately normally distributed, with standard deviation 18 units. A random sample of 81 days of output will be collected to conduct the test.
Continued. Using the critical value you calculated in the previous question, what is the probability of Type II error if the population mean is 205?
Continued. If the sample mean turns out to be 205, what is the conclusion of the test?
Answers
The manager wants to control the maximum probability of Type I error at 1% (i.e. the manager wants the significance level to be 1%). To calculate the critical value, we need to find the Z-score associated with a 1% significance level.
To find the critical value, we can use a Z-table or a Z-score calculator. Since the significance level is 1% (0.01), we need to find the Z-score corresponding to the area of 0.99 (1 - 0.01) in the upper tail of the standard normal distribution.
By looking up the Z-table or using a Z-score calculator, we find that the Z-score corresponding to a 0.99 cumulative probability is approximately 2.33. The critical value the manager should use to conduct the hypothesis test is 2.33.
To calculate the probability of Type II error, we need to specify an alternative hypothesis and determine the corresponding population mean value. In this case, the alternative hypothesis is that the mean daily output is greater than 200, and the specified population mean value is 205.
To calculate the probability of Type II error, we need to find the area under the null hypothesis distribution that falls to the right of the critical value. In other words, we need to find the probability that the test statistic, assuming the null hypothesis is true, falls in the rejection region. Since we are assuming the population mean is 205, we can calculate the Z-score using the formula:
Z = (sample mean - population mean) / (standard deviation / sqrt(sample size))
Substituting the values, we get:
Z = (205 - 200) / (18 / sqrt(81)) = 5 / (18 / 9) = 5 / 2 = 2.5
Now, we can calculate the probability of Type II error by finding the area under the null hypothesis distribution to the right of the critical value, which is 2.33. Using the Z-table or a Z-score calculator, we find that the probability of Type II error is approximately 0.0062, or 0.62%.
If the sample mean turns out to be 205, we compare it to the critical value. If the sample mean is greater than the critical value (2.33), we reject the null hypothesis. In this case, since the sample mean is 205, which is greater than the critical value of 2.33, we would reject the null hypothesis. The conclusion of the test would be that there is sufficient evidence to suggest that the mean daily output is greater than 200.
Let's learn more about probability:
https://brainly.com/question/25839839
#SPJ11
What is the relationship between 2 and 2?
Answers
As per the question, in context of mathematics the relation between 2 and 2 is equality relationship.
What is equality relationship in mathematics?n mathematics, an equality relationship is a relationship between two quantities or expressions that are equal to each other. This relationship is represented using the equals sign (=).
Why are relations important in mathematics?Relations are important in mathematics because they allow us to describe and analyze the relationships between different quantities or values. Relations can be used to describe how two quantities are related to each other, such as whether they are equal, greater than, or less than each other.
The relationship between 2 and 2 is that they are both equal to each other. In mathematics, two is a number that is equal to the sum of one plus one. It is a cardinal number, which means it is used to count the number of objects in a set. Two is also an even number, which means it is divisible by 2 without a remainder.
To learn more about relations in mathematics visit:
https://brainly.com/question/28980347
#SPJ4
A tank can hold 85 litres water . It's 30% filled. What percentage of the tank empty? Write answer in decimal and fraction
Answers
Answer:
59.50 liters (fraction from)
\(\dfrac{119}{2} \ in \ fraction \ form.\)
Step-by-step explanation:
30% of tank is filled. So, (100 - 30)% of tank is empty.
70% of tank is empty.
Capacity of the tank that is empty = 70% of 85 liters
In decimal form:
= 0.7 * 85
= 59.50 liters
In fraction form:
70% of 85 = \(\dfrac{70}{100}*85\)
\(= \dfrac{7}{2}*17\\\\=\dfrac{119}{2}\)
Find the 19th term of the sequence 5, 8, 11, 14, 17...
59
51
53
56
Answers
Answer:
59
Step-by-step explanation:
So, lets look at our numbers in the sequence. So it goes 5 to 8, 8 to 11, 11 to 14, and 14 to 17. This seems like a change in three. So the every 1 term changes the orginal 5 value by 3.
So wouldnt this mean we can multiply the change in terms by the amount of terms? Which is 19*3? Well, sort of. This is the right way of doig this, but we must remember that we already know the first term, 5. So this means we will be doing 18*3.
This gets you 54. Now just add the amount of the 18 terms onto the first term:
54+5
=
59
So your answer is 59.
Hope this helps!
Y is an exponential random variable with parameter ? = 0.35. Define the event A-fY < 2]. (a) Find the conditional PDF. 0 y2, otherwise (b) Calculate the conditional expected value.
Answers
(a) To find the conditional PDF of Y given the event A, we need to use the formula: \(f(Y|A) = f(Y and A)/P(A)\) and integration method.
We know that Y has an exponential distribution with a parameter \(λ = 0.35\), so its PDF is: \(f(Y) = λe^(-λy), for y ≥ 0\). To find f(Y and A), we need to calculate the probability that both events occur: \(f(Y and A) = P(Y < 2 and Y = y) = P(Y < 2) * P(Y = y)\) =\(∫0^2 λe^(-λy) dy = -e^(-0.7y) from 0 to 2 = e^(-1.4) - 1\)
The probability of event A is: \(P(A) = P(Y < 2)\)= \(∫0^2 λe^(-λy) dy\)= \(-e^(-0.7y)\)from 0 to 2 = \(e^(-1.4) - 1\)
Therefore, the conditional PDF of Y given event A is:
\(f(Y|A) = f(Y and A)/P(A) = (λe^(-λy))/(e^(-1.4) - 1), for 0 ≤ y < 2\)
\(f(Y|A) = 0, for y ≥ 2\)
(b) The conditional expected value of Y given event A is:
\(E(Y|A) = ∫0^2 yf(Y|A) dy = ∫0^2 y(λe^(-λy))/(e^(-1.4) - 1) dy\)
Using integration by parts, we get:
\(E(Y|A) = [-y*e^(-0.35y)/(2-2e^(-1.4))] from 0 to 2 + ∫0^2 e^(-0.35y)/(2-2e^(-1.4)) dy\)
\(E(Y|A) = [-y*e^(-0.35y)/(2-2e^(-1.4))] from 0 to 2 + [-20/(7e^(1.4)-7)]\)
\(E(Y|A) = 1.2276\)
To learn more about integration, visit here
https://brainly.com/question/30900582
#SPJ4
Pls help thank you will mark the Brainliest

Answers
The exponential equation is given by the function y = 30.5(0.7)ˣ
What is an equation?An equation is an expression that shows how numbers and variables are linked together using mathematical operations such as addition, subtraction, multiplication and division.
The standard form of an exponential equation is:
y = abˣ
where b is the rate of change and a is the initial value.
Let y represent the number of games sold x years since 2015.
From the graph, at point (0, 30.5):
30.5 = ab⁰
a = 30.5
Also, at point (1, 21.35):
21.35 = ab¹; but a = 30.5, hence:
21.35 = 30.5b
b = 0.7
The equation is y = 30.5(0.7)ˣ
Find out more on equation at: https://brainly.com/question/2972832
#SPJ1
The Vertical position y (in feet) of a rock T seconds after it was dropped from a Cliff is given by the formula y= -60tsquared +4t+380. The base of a Clift corresponds to y=0 after how many seconds with a rock hit the ground at the base of the Cliff
Answers
Answer:
2.48 seconds
Step-by-step explanation:
The given function is
\(y=-60t^2+4t+380\)
When \(y=0\) the ball will be at the ground
\(0=-60t^2+4t+380\)
\(\Rightarrow t=\dfrac{-4\pm \sqrt{4^2-4\left(-60\right)\times 380}}{2\left(-60\right)}\)
\(\Rightarrow t=-2.48,2.55\)
So, the time taken by the rock to hit the ground is \(2.48\ \text{seconds}\).
Find the area of a triangle with the given base b and height h . b=6 in., h=15 in.
Answers
6 x 15 = 90
90/2 = 45
area = 45cm^2
Look at the image below. Identify the coordinates for point X, so that the ratio of AX : XB = 5 : 4
Answers
The coordinates of X that partitions XY in the ratio 5 to 4 include the following: X (-1.6, -7).
How to determine the coordinates of point X?In this scenario, line ratio would be used to determine the coordinates of the point X on the directed line segment AB that partitions the segment into a ratio of 5 to 4.
In Mathematics and Geometry, line ratio can be used to determine the coordinates of X and this is modeled by this mathematical equation:
M(x, y) = [(mx₂ + nx₁)/(m + n)], [(my₂ + ny₁)/(m + n)]
By substituting the given parameters into the formula for line ratio, we have;
M(x, y) = [(5(2) + 4(-6))/(5 + 4)], [(5(-11) + 4(-2))/(5 + 4)]
M(x, y) = [(10 - 24)/(9)], [(-55 - 8)/9]
M(x, y) = [-14/9], [(-63)/9]
M(x, y) = (-1.6, -7)
Read more on line ratio here: brainly.com/question/14457392
#SPJ1
Missing information:
The question is incomplete and the complete question is shown in the attached picture.
