Answers
Related Questions
what is the slope of the line that contains points (−3 −5) and (2 7)
Answers
Answer:
Step-by-step explanation:
To find the slope of a line when only given two points on that line, divide the difference in the y points by the difference in the x points.
slope = (-5 - 7)/(-3 - 2) = -12/-5 = 12/5
slope = (7 - -5)/(2 - -3) = 12/
The volume of a cube is decreasing at a rate of 210mm3/s. What is the rate of change of the cube’s surface area when its edges are 70mm long?
Answers
The rate of change of the cube's surface area when its edges are 70mm long is -0.014 mm/s.
This indicates that the surface area is decreasing at a rate of 0.014 \(mm^2/s.\)
To find the rate of change of the cube's surface area when its edges are 70mm long, we can use the formulas for the volume and surface area of a cube.
The volume of a cube is given by\(V = s^3,\) where s is the length of the cube's edges.
In this case, the volume is decreasing at a rate of 210mm^3/s.
Differentiating both sides of the equation with respect to time, we get \(dV/dt = 3s^2 ds/dt,\)
where dV/dt represents the rate of change of volume and ds/dt represents the rate of change of the edge length.
Since we are given that \(dV/dt = -210mm^3/s\) and s = 70mm, we can substitute these values into the equation and solve for ds/dt.
\(-210 = 3(70^2) ds/dt\)
-210 = 3(4900) ds/dt
\(ds/dt = -210 / (3 \times 4900)\)
ds/dt = -0.014 mm/s
Therefore, the rate of change of the cube's surface area when its edges are 70mm long is -0.014 mm/s.
This indicates that the surface area is decreasing at a rate of 0.014 \(mm^2/s.\)
For similar question on cube's surface area.
https://brainly.com/question/28776132
#SPJ11
Which of the following lists the numbers shown above in order from greatest to least?

Answers
Answer:
F
Step-by-step explanation:
the square root of 51 = 7.141
7 square root 2 = 9.899
7 = 7
8 = 8
The correct order of these numbers from greatest to least are
7√2, 8, √51, and 7.
We know there are two types of radicals one is surds when the number has been raised by such power that it is greater than zero and less than one,
The other type of radicals are indices where a number is raised to such power that is greater than one.
We know √2 is approximately 1.414.
Given, √51, 7√2, 8, and 8.
Now, A perfect square number nearest to √51 is √49 which is 7 so √51 is just more than 7.
Between 8 and 7√2, 7√2 is greater than 8 because is multiplied by approximately 1.5 times, So the correct order of these numbers are,
7√2, 8, √51, and 7.
learn more about surds and indices here :
https://brainly.com/question/28093573
#SPJ2
write a rule for the nth term of geometric sequence a1= 3 and r= 1/2
Answers
The formula for the n-th term is:
aₙ = 3*(1/2)⁽ⁿ⁻¹⁾
How to find the rule for the n-th term?For a geometric sequence where the first term is a₁ and the common ratio is r, the formula for the n-th term is:
aₙ = a₁*(r)⁽ⁿ⁻¹⁾
Here we know that the first term is a₁ = 3 and the common ratio is r = 1/2.
Then the formula for the n-th term of the sequence is:
aₙ = 3*(1/2)⁽ⁿ⁻¹⁾
Learn more about geometric sequences at:
https://brainly.com/question/24643676
#SPJ1
Use the properties of operations to determine if the expressions are equivalent. 3+y;1/3(6+y)
Answers
The properties of operations used here are the distributive property of multiplication over addition.
Given expressions in the question
3+y and 1/3(6+y)
We need to check whether they are equivalent or not.
For that, let's simplify the second expression by multiplying with the reciprocal of the coefficient of y.
1/3(6+y) = (1/3) * 6 + (1/3) * y= 2 + (1/3)y
Therefore, the given expressions are equivalent.
The properties of operations used here are the distributive property of multiplication over addition.
This property is used to simplify the expression 1/3(6+y) to 2 + (1/3)y.
or
1/3(6+y) / 2 + (1/3)y
To know more about multiplication, visit
https://brainly.com/question/11527721
#SPJ11
the file at he bottom

Answers
Answer:
I don't see anything
Step-by-step explanation:
What is the area of the shaded region in the given circle in terms of pi and in simplest form?
A) (120pi + 6 sqrt 3) m^2
B) (96pi + 36 sqrt 3) m^2
C) (120pi + 36 sqrt 3) m^2
D) (96pi + 6 sqrt 3) m^2

Answers
Answer:(120pi +6 square root 3) msquared
Step-by-step explanation:
Describe the relationship between quartiles and percentiles. ▼ are special cases of ▼ ▼ Upper Q 2 Upper Q 3 Upper Q 1 is the 25th percentile, ▼ Upper Q 2 Upper Q 1 Upper Q 3 is the 50th percentile, and ▼ Upper Q 2 Upper Q 3 Upper Q 1 is the 75th percentile.
Answers
Answer:
Q1 is the 25th percentile
Step-by-step explanation:
Quartiles are known to be one-fourth of an entity, that is, 1/4th with the whole evaluating to 1. The numerator cannot exceed four, as the division compares an item in an entity to the whole of the entity or sample.
Percentiles represents a whole entity as a 100 with the symbol "%" which denote its use.
The first quartile is 25th percentile, the second is the 50th percentile, the third is the 75th percentile while the fourth quartile which is 4/4 is the 100th percentile mark.
Juan makes 75% of the goals he attempted during soccer practice. If he makes 30 goals at practice, how many does he attempt?
Answers
Answer:
22.5
Step-by-step explanation:
30/4=7.5
7.5 times 3 = 22.5
Mark brainliest plz!
I need help with this like right now

Answers
Answer:
125º
Step-by-step explanation:
An exterior angle of a triangle is equal to the sum of its opposite interior angles.
In this case, 146º is the exterior angle and 21º and xº are the interior angles.
We can set up an equations 146=21+x
By subracting 21, we find that x=125
Answer:
\(\boxed{\boxed{\tt x=125^{\circ}}}\)
Step-by-step explanation:
To solve this problem we need to apply the triangle exterior angle property.
*Exterior angle of a triangle is equal to the sum of its two opposite interior angles.*
146 ° here, is an exterior angle of the triangle, and 21 °/x are opposite interior angles.
\(\tt 146^{\circ}=21^{\circ}+x\)
Switch sides:
\(\longmapsto\tt 21^{\circ}+x=146^{\circ}\)
Subtract 21 from both sides:
\(\longmapsto\tt 21^{\circ}+x-21^{\circ}=146^{\circ}-21^{\circ}\)
\(\longmapsto\tt x=125^{\circ}\)
________________________________what number is between 0-5
Answers
Answer:
3? ;-;
Step-by-step explanation:
Is (x+4) a factor of the polynomial x^3+8x^2+11x-20? Explain
Answers
Answer:
yes
Step-by-step explanation:
if (x + a) is a factor of f(x), then f(- a) = 0, Factor theorem
given
f(x) = x³ + 8x² + 11x - 20
then if (x + 4) is a factor f(- 4) = 0
f(- 4) = (- 4)³ + 8(- 4)² + 11(- 4) - 20
= - 64 + 8(16) - 44 - 20
= - 64 + 128 - 64
= 0
since f(- 4) = 0 , then (x + 4) is a factor of the polynomial
lestion 7 In presenting Resource-Advantage (RA) theory, Hunt and Lambe (2000) use a boxes-and- ot yet niswered oints out of arrows diagram called, "A Schematic of RA Theory of Competition, These boxes are 00 a. Resources, Debt, Financial Performance y Flag question b. Debt, Market Position, Financial Performance c. none of the above d. Resources, Market Position, Debt e. Resources, Market Position. Financial Performance
Answers
The correct combination of boxes in the diagram is: Resources, Market Position, and Debt. These three elements are central to the RA theory and are interconnected in their influence on a firm's competitive advantage and performance.
In presenting Resource-Advantage (RA) theory, Hunt and Lambe (2000) use a boxes-and-arrows diagram called "A Schematic of RA Theory of Competition." This diagram illustrates the key elements of the theory and their relationships. The boxes in the diagram represent important components or factors, while the arrows indicate the directional relationships between these components.
Resources refer to the tangible and intangible assets that a firm possesses, including physical, financial, human, and intellectual resources. These resources provide the foundation for a firm's competitive advantage and can include factors such as technology, brand reputation, skilled workforce, and financial capital.
Market Position represents a firm's strategic positioning within its target market. It encompasses factors such as customer perceptions, market share, competitive differentiation, and market reputation. A strong market position enables a firm to leverage its resources effectively and gain a competitive edge.
Debt refers to the financial obligations or liabilities that a firm has, including loans, bonds, and other forms of debt financing. Debt can impact a firm's financial performance and stability, as well as its ability to invest in resources and maintain its market position.
By considering the interplay between resources, market position, and debt, the RA theory emphasizes how firms can leverage their resource advantages to strengthen their market position and achieve better financial performance. This framework highlights the importance of aligning these elements strategically and efficiently managing resources and debt to gain a sustainable competitive advantage in the marketplace.
Learn more about resources here:
brainly.com/question/24468826
#SPJ11
Find the directional derivative of f at the given point in the direction indicated by the angle θ. f(x, y) = xy^3 − x^2, (1, 4), θ = π/3
Answers
The directional derivative of a function f(x, y) at a point (a, b) in the direction of a unit vector u = ⟨cosθ, sinθ⟩ is given by the dot product of the gradient of f at (a, b) and the unit vector u.
That is, D_uf(a, b) = ∇f(a, b) · u
Here, f(x, y) = xy^3 - x^2, so ∇f(x, y)
= ⟨y^3 - 2x, 3xy^2⟩.
At the point (1, 4), we have ∇f(1, 4) = ⟨60, 192⟩.
The direction indicated by the angle theta = π/3 is u = ⟨cos(π/3), sin(π/3)⟩ = ⟨1/2, √3/2⟩.
Therefore, the directional derivative of f at (1, 4) in the direction of u is:
D_uf(1, 4) = ∇f(1, 4) · u
= ⟨60, 192⟩ · ⟨1/2, √3/2⟩
= 60/2 + 192(√3/2)
= 30 + 96√3
So the directional derivative of f at (1, 4) in the direction of θ = π/3 is 30 + 96√3.
Learn more about derivative, here:
brainly.com/question/23819325
#SPJ11
If two events are independent, then their joint probability is computed with _____.
A. the special rule of addition
B. the special rule of multiplication
C. the general rule of multiplication
D. the bayes theorem
Answers
B. the special rule of multiplication.
The joint probability of two independent events is computed using the special rule of multiplication.
What is the method used to calculate the joint probability of two independent events?When two events are independent, their joint probability is calculated using the special rule of multiplication.
This rule states that the probability of both events occurring together is equal to the product of their individual probabilities. In other words, if A and B are two independent events, then the probability of A and B occurring together is equal to the probability of A multiplied by the probability of B.
For example, if the probability of event A is 0.4 and the probability of event B is 0.5, then the probability of both events occurring together is 0.4 x 0.5 = 0.2.
Learn more about probability
brainly.com/question/31828911
#SPJ11
y=9x -7 in standard form
Answers
Answer:
change to standard form
-9x+y=4
multiply through by -1
9x-y=-4
Can you please hurry I only have like 25 minutes left

Answers
Answer:
Step-by-step explanation:
Answer:
The one you selected is correct.
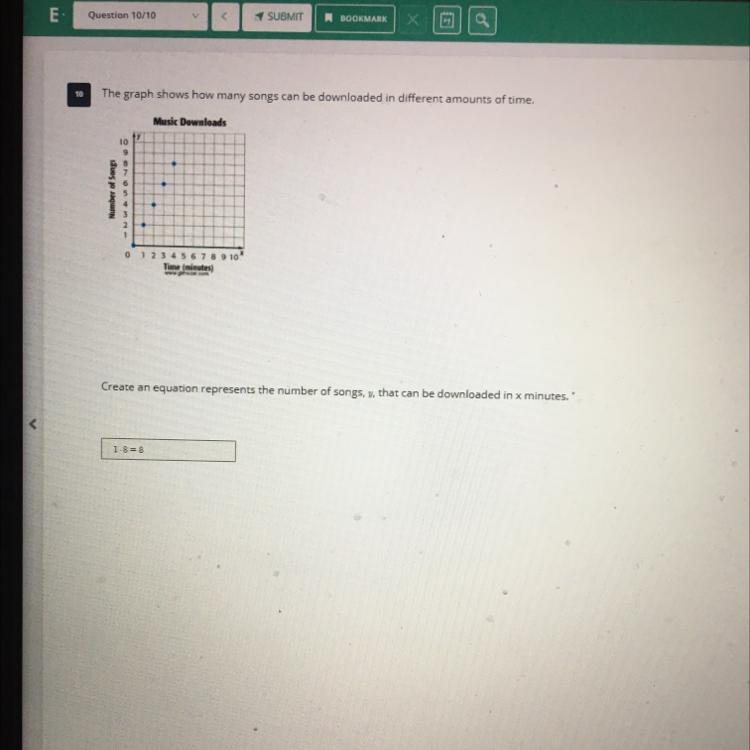
14. In the 6-sided figure below, adjacent sides meet at right angles and
the lengths given are in centimeters. What is the area of the figure, in centimeters?
Answers
The total area of the composite figure is 228 sq cm
Calculating the area of the figureFrom the question, we have the following parameters that can be used in our computation:
The composite figure with 6 sides
The total area of the composite figure is the sum of the areas of the individual shapes
So, we have
Area = Area of Rectangle + Area of Rectangle
Using the above as a guide, we have the following equation
Area = 12 * 14 + (22 - 12) * 6
Evaluate the products
Area = 228
Hence, the total area of the figure is 228 sq cm
Read more about area at
brainly.com/question/26403859
#SPJ1
What are not changed after a rotation
Answers
Answer: b
Step-by-step explanation:
You have a circular mirror. The mirror has a diameter of 8 inches. There is a circular frame around the mirror. If the mirror and frame together have a radius of 6 inches, what is the area of just the frame?
Answers
Answer:
20
Explanation:
The mirror and the frame together have a radius of 6 inches, and since the diameter of the mirror is 8 inches, the radius of the mirror is 4 inches.
To find the area of just the frame, we need to subtract the area of the mirror from the area of the frame and mirror combined.
The area of the frame and mirror combined can be calculated as the area of a circle with a radius of 6 inches:
Area of frame and mirror = πr^2 = π(6)^2 = 36π square inches.
The area of the mirror can be calculated as the area of a circle with a radius of 4 inches:
Area of mirror = πr^2 = π(4)^2 = 16π square inches.
Therefore, the area of just the frame is:
Area of frame = Area of frame and mirror - Area of mirror
= 36π - 16π
= 20π square inches.
So, the area of just the frame is 20π square inches, which is approximately 62.83 square inches if we use 3.14 as an approximate value for π.
Hopefully this helps!
Choose the point-slope form of the equation below that represents the line that passes through the points (−6, 4) and (2, 0)

Answers
Answer:
B. y - 4 = - 1/2(x + 6)Step-by-step explanation:
Given points on the line:
(−6, 4) and (2, 0)Find the slope:
m = (0 - 4)/(2 - (-6)) = -4/ 8 = -1/2Point slope form using the first point:
y - 4 = - 1/2(x - (- 6)) ⇒ y - 4 = - 1/2(x + 6)Correct choice is B
\(▪▪▪▪▪▪▪▪▪▪▪▪▪ {\huge\mathfrak{Answer}}▪▪▪▪▪▪▪▪▪▪▪▪▪▪\)
The required equation is :
\(\boxed{ \boxed{y - 4 = - \dfrac{1}{2} (x + 6)}}\)
\( \large \boxed{ \mathfrak{Explanation}}\)
Let's find the slope (m) ~
\( \mathrm{\dfrac{y_2 - y_1}{x_2 - x_1} }\)\( \dfrac{4 - 0}{ - 6 - 2} \)\( - \dfrac{4}{8} \)\( - \dfrac{ 1 }{2} \)now, let's use the slope and the points to write the equation of line in point slope form ~
\(y - 4 = - \dfrac{ 1}{2} (x - ( - 6))\)\(y - 4 = - \dfrac{1}{2} (x + 6)\)Please help answer this! write all names that apply to both numbers (integer,rational,irrational,real,whole)

Answers
Answer:
8. integer, rational, real, whole
9. irrational, real
solve the problem. round your answer, if appropriate. a ladder is slipping down a vertical wall. if the ladder is 17 ft long and the top of it is slipping at the constant rate of 2 ft/s, how fast is the bottom of the ladder moving along the ground when the bottom is 8 ft from the wall?
Answers
The speed of the bottom of the ladder moving along the ground when the bottom is 8 ft from the wall is 3.75 ft/sec.
What is speed?
The distance travelled in relation to the time it took to travel that distance is how speed is defined. Since speed simply has a direction and no magnitude, it is a scalar quantity.
Let us take x = the distance from the base of the ladder to the base of the wall.
y = the distance from the tip of the ladder to the base of the wall, we have:
=> \(x^2 + y^2 = 17^2\)
=> \(y^2=17^2-x^2=17^2-8^2=289-64=225=15^2\)
=> y = 15 ft.
Now differentiate then,
=> 2x dx/dt + 2y dy/dt = 0
=> 2 * 8 * dx/dt + 2 * 15 * (-2) = 0
=> 16 dx/dt = 60
=> dx/dt = 60/16= 3.75 ft/sec
Hence the bottom of the ladder moving along the ground when the bottom is 8 ft from the wall is 3.75 ft/sec.
To learn more about Speed refer the below link
https://brainly.com/question/13262646
#SPJ1
A function is given.f(x) = 3x − 8; x = 2, x = 3(a) Determine the net change between the given values of the variable.(b) Determine the average rate of change between the given values of the variable.
Answers
The net change between the values of the variable x=2 and x=3 for the function f(x)=3x-8 is 1. The average rate of change between the values of x=2 and x=3 for the function f(x)=3x-8 is 3.
(a) The net change between the given values of the variable is determined by subtracting the function value at x = 2 from the function value at x = 3.
f(3) - f(2) = (33) - 8 - [(32) - 8] = 1
Therefore, the net change between the given values of the variable is 1.
(b) The average rate of change between the given values of the variable is determined by dividing the net change by the difference in the values of the variable.
Average rate of change = (f(3) - f(2))/(3-2) = (1/1) = 1
Therefore, the average rate of change between the given values of the variable is 1.
The net change between two points on a function is the difference in the function values at those points. In this case, the function values at x = 2 and x = 3 are 2 and 1, respectively. Therefore, the net change between these two points is 1.
The average rate of change between two points on a function is the slope of the line connecting those two points. In this case, the two points are (2, f(2)) and (3, f(3)). The slope of the line connecting these two points is the same as the average rate of change between these two points. The formula for the slope of the line passing through two points is (y2-y1)/(x2-x1), which is the same as the average rate of change formula. Therefore, the average rate of change between x = 2 and x = 3 is equal to the slope of the line connecting the two points, which is 1.
To learn more about slopes, visit:
https://brainly.com/question/27877215
#SPJ11
Fill out the x-y chart. 11. y = log_2 x – 1 X -2 -1 O 1 2 Y C
ASAP!!!!

Answers
Answer:
\(\begin{array}{|c|c|}\cline{1-2}\vphantom{\dfrac12}x&y\\\cline{1-2}\vphantom{\dfrac12}-2&\rm DNE\\\cline{1-2}\vphantom{\dfrac12}-1&\rm DNE\\\cline{1-2}\vphantom{\dfrac12}0&\rm DNE\\\cline{1-2}\vphantom{\dfrac12}1&-1\\\cline{1-2}\vphantom{\dfrac12}2&0\\\cline{1-2}\end{array}\)
Step-by-step explanation:
Given equation:
\(y=\log_2x-1\)
To fill out the given x-y chart, substitute each given value of x into the given log equation.
The argument of a log function can only take positive arguments, so when x = -2, x = -1 and x = 0, the y-values are undefined.
The values of y for x = 1 and x = 2 are:
\(\begin{aligned}x=1 \implies y&=\log_21-1\\&=0-1\\&=-1\end{aligned}\)
\(\begin{aligned}x=2 \implies y&=\log_22-1\\&=1-1\\&=0\end{aligned}\)
Therefore, the completed x-y chart for the equation y = log₂x - 1 is:
\(\begin{array}{|c|c|}\cline{1-2}\vphantom{\dfrac12}x&y\\\cline{1-2}\vphantom{\dfrac12}-2&\rm DNE\\\cline{1-2}\vphantom{\dfrac12}-1&\rm DNE\\\cline{1-2}\vphantom{\dfrac12}0&\rm DNE\\\cline{1-2}\vphantom{\dfrac12}1&-1\\\cline{1-2}\vphantom{\dfrac12}2&0\\\cline{1-2}\end{array}\)
Note: I have used DNE for does not exist.
Keisha is playing a game using a wheel divided into 8 equal sectors, as shown in the diagram below. Each time the spinner lands on blue, she will win a prize. If Keisha spins this wheel twice, what is the probability that she will win a prize on both spins?
Answers
In a wheel game with eight equally spaced sectors, Keisha's chances of winning a reward on both spins are 1/16.
What is a probability example?Probability—the possibility that an occurrence will happen—is calculated by dividing here the same number of favorable outcomes by the total number of possible outcomes. A coin toss serves as the most simple instance. If you flip a coin, there are only two possible outcomes: heads or tails.
The spinners will get a reward each everytime she lands on white. She will spin the wheel twice.
Here, there are two instances of such color white in the wheel, and there are a total of eight sectors. the likelihood that white will appear in the spin for the first time is,
P = 2/8
P = 1/4
The second case's circumstances are the same. In this instance, the outcomes including both wheel revolutions are independent of one another.
According to the product rule, the likelihood that a white sector will both spin and emerge is,
P = 1/4 * 1/4
P = 1/16
In a wheel game with eight equally spaced sectors, Keisha has a 1/16 chance of winning a reward on both spins.
To know more about Probability visit:
https://brainly.com/question/24756209
#SPJ1
The complete question is-
Keisha is playing a game using a wheel divided into eight equal sectors, as shown in the diagram. Each time the spinner lands on white, she will win a prize. If she spins this wheel twice, what is the probability she will win a prize on both spins? Please show all steps!

Tell how much each person gets when they share equally.
3 friends share 5 pounds of trail mix.

Answers
Answer:
1.7 pounds each friend gets
Step-by-step explanation:
\(3 \: friends \: share \: 5 \: pounds \: of \: trail \: mix \\ 5 \: pound \: \div 3 \\ = 1.66666666666 \\ approximately \\ = 1.7(to \: 1 \: decimal \: place\)
can you guys answer these sequences?

Answers
b) 7, 17, 27, 37
-3,7,17,27,37
A phone company charges for service according to the formula
C(n) = 22 + 0.1n,
where n is the number of minutes talked, and
C(n)
is the monthly charge, in dollars.
Answers
Please help me with this question so I can better help my son to understand this better. I have attached the graph that were working from below? The graph shows f(x)and its transformation g(x).Enter the equation for g(x) in the box.g(x) =
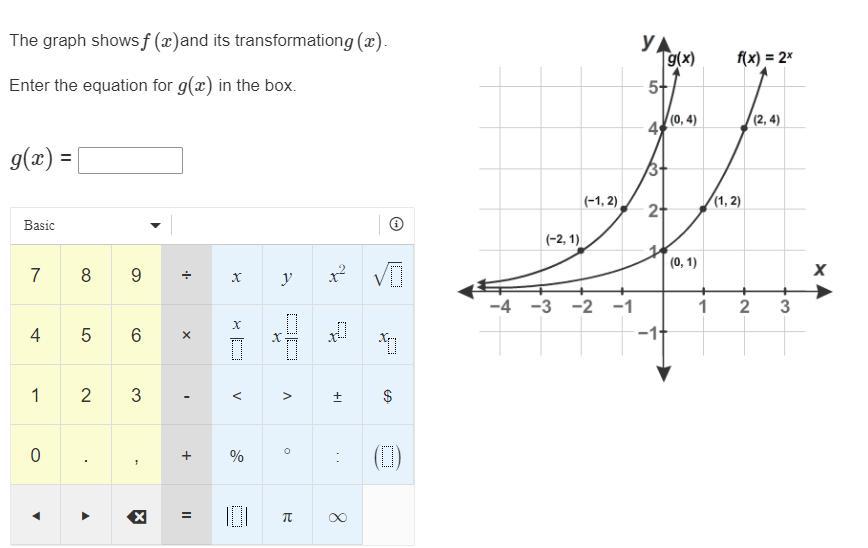
Answers
Answer
g(x) = 2ˣ⁺² or 2^(x + 2)
\(g(x)=2^{x+2}\)
Explanation
When a function f(x) is translated horizontally along the x-axis by a units, the new function is represented as
f(x + a) when the translation is by a units to the left.
f(x - a) when the translation is by a units to the right.
Looking at the coordinates of the points given on f(x) and g(x), we can see that g(x) is just f(x) translate 2 units to the left.
Hence, if f(x) = 2ˣ
g(x) = f(x + 2) = 2ˣ⁺² or 2^(x + 2)
Hope this Helps!!!