Which ordered pair is a solution of the equation?
7x – 2y = -5
Answers
Related Questions
Solve the problem. Round dollar amounts to the nearest cent. Use ordinary interest (360 days in a year) unless otherwise indicated. Chris Owens bought a new computer system. To pay for the system, he borrowed $3,290 from the credit union at 10(1/3)% interest for 110 days. Find the interest.
Answers
To find the interest of Chris Owens’ credit union loan of $3,290 at 10(1/3)% interest for 110 days, we use the simple interest formula as follows:
Simple Interest = (P × R × T)/100Where:P = Principal or amount borrowedR = Rate of interest per annumT = Time in years or fraction of a year110 days ÷ 360 days = 0.3056 (time as a fraction of a year)The rate of interest, 10(1/3)% is equal to 10 + (1/3) percent = 10.33% per annum in decimal form = 0.1033Substituting the values we have into the formula,Simple Interest = (P × R × T)/100= (3,290 × 0.1033 × 0.3056)/100= $100.68 (rounded to the nearest cent)
Therefore, the interest of Chris Owens’ credit union loan of $3,290 at 10(1/3)% interest for 110 days is $100.68.
A credit union loan is a type of personal loan that can be used for a variety of purposes. One of the most common reasons people take out credit union loans is to purchase big-ticket items like a new computer system. When you take out a loan, you must pay back the amount borrowed plus the interest charged by the lender. The interest rate is usually expressed as a percentage of the amount borrowed and is charged for a specific period of time known as the loan term. Simple interest is a method of calculating interest that is charged only on the principal amount borrowed.
It does not take into account the interest that has already been paid. Simple interest is calculated by multiplying the principal amount borrowed by the interest rate and the length of the loan term. The answer is more than 100 words.The interest of Chris Owens’ credit union loan of $3,290 at 10(1/3)% interest for 110 days is $100.68. Therefore, he would pay $3,290 + $100.68 = $3,390.68 in total to the credit union over the loan term. It is important to note that when rounding dollar amounts to the nearest cent, amounts that end in .50 or higher are rounded up to the next highest cent, while amounts that end in .49 or lower are rounded down to the next lowest cent. In this case, $100.6847 would be rounded up to $100.68. In conclusion, the interest charged on a loan can significantly increase the total amount that must be repaid, making it important for borrowers to understand how interest is calculated and the terms of their loan.
To know more about Chris Owens’ visit
https://brainly.com/question/11904608
#SPJ11
Simplify. Rewrite the expression in the form a^na n a, start superscript, n, end superscript. a^{5}\cdot a^{-3}=a 5 ⋅a −3
Answers
Answer:
The expression simplified is a^2
Step-by-step explanation:
Here, we are interested in writing the product as a single value.
We have; a^5 • a^-3
This is same as a^5 * a^-3
We proceed here using the first law of indices;
It would result to a^5 * a^-3 = a^(5-3) = a^2
Answer:
Step-by-step explanation:

a^3b^-2/ab^-4
Assume a can’t equal 0 and b can’t equal 0
Answers
Describe and correct the error in setting up the trigonometric function.

Answers
The value of side length w is 13.75 .
Given right angled triangle,
Perpendicular = w
Hypotenuse = 17
Angle of triangle = 54°
So,
According to the trigonometric ratios,
tanФ = p/b
cosФ = b/h
sinФ = p/h
By using sinФ,
sinФ = p/h
sin 54° = w/ 17
0.809 = w/17
w = 13.75 .
Thus after correction w will be 13.75
Know more about trigonometry,
https://brainly.com/question/25618616
#SPJ1
Please solve the attached problem with all steps.
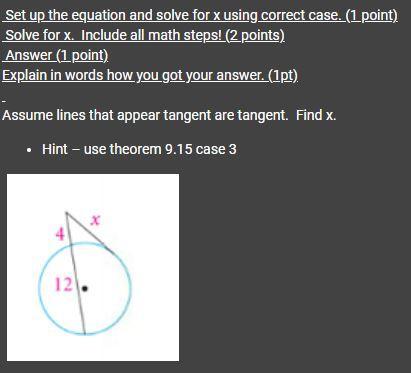
Answers
Answer:
x = 8
Step-by-step explanation:
Theorem
When a secant segment and a tangent segment meet at an exterior point, the square of the measure of the tangent segment is equal to the product of the measures of the secant segment and its external secant segment.
Secant: a straight line that intersects a circle at two points
Tangent: a straight line that touches a circle at only one point
Given:
tangent segment = xsecant segment = 4 + 12 = 16external secant segment = 4⇒ x² = 16 · 4
⇒ x² = 64
⇒ x² = √(64)
⇒ x = ±8
As distance is positive, x = 8
An Austrian study was completed to determine if untrained sea lions and sea lionesses could follow various experimenter-given cues when given a choice of two objects. One experimenter-given cue was to point at one of the objects. One sea lioness, named Zwerg, successfully chose the pointed-at object 37 times out of 48 trials. Does this result show that Zwerg can correctly follow this type of direction by an experimenter more than 50% of the time?ââ
Answers
Using the z-distribution, it is found that since the test statistic is greater than the critical value for the right-tailed test, this result shows that Zwerg can correctly follow this type of direction by an experimenter more than 50% of the time.
What are the hypothesis?At the null hypothesis, it is tested if Zwerg cannot correctly follow this type of direction by an experimenter more than 50% of the time, that is:\(H_0: p \leq 0.5\)
At the alternative hypothesis, it is tested if Zwerg can correctly follow this type of direction by an experimenter more than 50% of the time, that is:\(H_1: p > 0.5\)
Test statisticThe test statistic is given by:
\(z = \frac{\overline{p} - p}{\sqrt{\frac{p(1-p)}{n}}}\)
In which:
\(\overline{p}\) is the sample proportion.p is the proportion tested at the null hypothesis.n is the sample size.For this problem, the parameters are:
\(n = 48, \overline{p} = \frac{37}{48} = 0.7708, p = 0.5\)
The value of the test statistic is:
\(z = \frac{\overline{p} - p}{\sqrt{\frac{p(1-p)}{n}}}\)
\(z = \frac{0.7708 - 0.5}{\sqrt{\frac{0.5(0.5)}{48}}}\)
\(z = 3.75\)
Considering a right-tailed test, as we are testing if the proportion is greater than a value, with a significance level of 0.05, the critical value for the z-distribution is \(z^{\ast} = 1.645\).
Since the test statistic is greater than the critical value for the right-tailed test, this result shows that Zwerg can correctly follow this type of direction by an experimenter more than 50% of the time.
To learn more about the z-distribution, you can take a look at https://brainly.com/question/16313918
Please help ASAP!!!!!!

Answers
Answer:
what are the answer choices. List them out and do the process of elimination and we could go from there ig
Step-by-step explanation:
I need answer Immediately pls!!!!!!!

Answers
Answer:
12 or 1/12
Step-by-step explanation:
Looking at this equation it tells us that the spinner has 12 spaces that are labeled 1-12. And its asking to use the numbers to find the probability of the multiples of both 3 and 4.
So list them out:
3: 0, 3, 6, 9, 12, 15, 18 and so on
4: 0, 4, 8, 12, 20, 24 and so on
So as you can see 12 is a multiple of both numbers. So that is your answer. Hope this helped :)
Write an equation for the nth term of the arithmetic sequence. Then find a50.
8, 2, -4, - 10,
Answers
Explanation:
Write an equation for nth term:
a + d(n - 1)
a = 8 (first term)
d = -6 (common difference)
8 - 6(n - 1)
= 8 - 6n + 6
= -6n + 14
Find a 50:
-6(50) + 14
= -300 + 14
= -286
The equation for the nth term of the arithmetic sequence is -6n + 14 and the found 50 is -286.
What is an arithmetic sequence?An arithmetic sequence is a series of numbers that are ordered and share a common difference between each succeeding term. In the arithmetic sequence 3, 9, 15, 21, 27, for example, the common difference is 6.
Arithmetic is the branch of mathematics that studies numbers by performing various operations on them. A sequence is a numerically ordered list. The three dots indicate that the pattern should be continued. The difference is six.
a + d(n - 1)
a = 8 (first term)
d = -6 (common difference)
8 - 6(n - 1)
= 8 - 6n + 6
= -6n + 14
Find a 50:
-6(50) + 14
= -300 + 14
= -286
Therefore, the equation for the nth term of the arithmetic sequence is -6n + 14.
To learn more about an arithmetic sequence, refer to the link:
https://brainly.com/question/29616017
#SPJ2
Which team has more consistent swim times? WILL CHOOSE BRAINLIEST

Answers
Answer:
Sunrise Sharks
Step-by-step explanation:
I added all of the numbers then divided them by 5 since there are 5 swim times provided. Have a nice day!
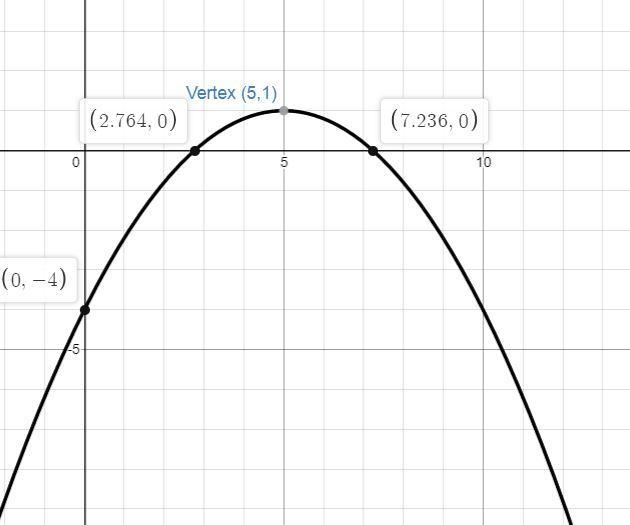
Graph the function. f(x) = 1/5x^2 + 2x - 4

Answers
The x-coordinate of vertex of parabola is,
\(x=-\frac{b}{2a}\)Determine the vertex of parabola.
\(\begin{gathered} x=-\frac{2}{2\cdot(-\frac{1}{5})} \\ =5 \end{gathered}\)Substitute 5 for x in the function to obtain the y-coordinate of vertex.
\(\begin{gathered} f(5)=-\frac{1}{5}\cdot(5)^2+2\cdot5-4 \\ =-5+10-4 \\ =1 \end{gathered}\)So vertex of parabola is (5,1).
Determine the roots of the function.
\(\begin{gathered} x=\frac{-2\pm\sqrt[]{(2)^2-4\cdot(-\frac{1}{5})\cdot(-4)}}{2\cdot(-\frac{1}{5})} \\ =\frac{-2\pm\sqrt[]{4-3.2}}{-0.4} \\ =\frac{-2\pm0.894}{-0.4} \\ \approx2.764,7.236 \end{gathered}\)Thus function intrsects the x axis at (2.764,0) and (7.236,0).
The function intersect the y-axis at (0,-4).
Plot the function on graph.
On a coordinate plane, a straight line crosses the y-axis at (0, 0). On a coordinate plane, a straight line crosses the y-axis at (0, negative 2). On a coordinate plane, a straight line crosses the y-axis at (0, negative 3). On a coordinate plane, a straight line crosses the y-axis at (0, 3).
Answers
Answer:
On a coordinate plane, a straight line crosses the y-axis at (0, 0)
Step-by-step explanation:
Required
Which represents a proportion
For a graph to represent a proportion, the line of the graph must pass through the origin (i.e. it must pass through (0,0))
From the list of options, only option (a) passes through (0,0).
Other options (b - d) pass through points other than the origin.
Hence, (a) is correct
During take off, a plane leaves the ground and
travels in a straight line until it reaches a
height of 8 km. The distance the plane flies
during take off should be in the range 44 km
to 49 km.
What is the smallest possible angle that the
path of the plane could make with the ground?
Give your answer in degrees to 1 d.p.

Answers
The smallest possible angle that the path of the plane could make with the ground is 9.3 degrees to 1 decimal place.
How to find the smallest possible angleTo find the smallest possible angle that the path of the plane could make with the ground, we need to use trigonometry.
Let's assume that
the angle we're looking for is θ, and the distance traveled by the plane is d.We know that the height reached by the plane is 8 km, which means that:
tan θ = 8 / d
We also know that the distance traveled by the plane should be in the range 44 km to 49 km. This means that:
44 ≤ d ≤ 49
To find the smallest possible angle θ, we need to find the largest possible value of d that satisfies the above inequality.
tan θ = 8 / 49
θ = arc tan (8 / 49)
θ = 9.2726
θ ≈ 9.3°
Learn more about angle at:
https://brainly.com/question/25716982
#SPJ1
as the spacing between joists increases, the maximum span for any board size: A. increases only. B. decreases only. C. increases and then decreases. D. decreases and than increases
Answers
As the spacing between joists increases, the maximum span for any board size will B. decrease only. This is because the wider the spacing between joists, the more weight and pressure will be placed on the boards that are spanning the gap between them.
This means that the boards will need to be stronger in order to support the weight without bending or breaking.
If the boards are not strong enough, they may sag or bow under the weight, which can create safety hazards or damage to the structure. Therefore, it is important to use the appropriate board size and spacing between joists for any given application in order to ensure structural integrity and safety.
In summary, increasing the spacing between joists will result in a decrease in the maximum span for any board size, as the boards will need to be stronger in order to support the weight and pressure. It is important to choose the right board size and joist spacing to maintain the structural integrity and safety of the building or structure.
To learn more about joists, refer:-
https://brainly.com/question/1927626
#SPJ11
Find the differential of each function. y = tan squareroot 3t y = 4 - v^2/4 + v^2
Answers
The differentials of the given functions are:
dy/dt = (1/2)√(3t) sec^2(√(3t)) dt
dy/dv = -v/2 + v
To find the differential of the function y = tan(sqrt(3t)), we can use the chain rule. Let u = sqrt(3t). Applying the chain rule, we have dy/dt = dy/du * du/dt.
First, we find dy/du by taking the derivative of tan(u), which is sec^2(u). Then, we find du/dt by taking the derivative of sqrt(3t), which is (1/2)√(3t). Multiplying these two derivatives together, we get dy/dt = (1/2)√(3t) sec^2(√(3t)) dt.
To find the differential of the function y = 4 - v^2/4 + v^2, we need to take the derivative with respect to v. The first term, 4, does not depend on v, so its derivative is 0.
For the second term, -(v^2/4), we use the power rule for differentiation. The derivative of v^2 is 2v, and dividing by 4 gives -(v/2).
For the third term, v^2, the derivative is 2v.
Combining these derivatives, we get dy/dv = -v/2 + v.
The differentials of the given functions have been calculated as dy/dt = (1/2)√(3t) sec^2(√(3t)) dt and dy/dv = -v/2 + v. These differentials represent the rate of change of the functions with respect to the respective variables.
To know more about differentials visit:
https://brainly.com/question/1164377
#SPJ11
The differential of y = tan(sqrt(3t)) is dy/dt = (1/2)(3t)^(-1/2)(3)(sec^2(sqrt(3t))). The differential of y = 4 - v^2/4 + v^2 is dy/dv = 3v/2.
To find the differential of each function, we will differentiate them with respect to the independent variable.
Differentiation of y = tan(sqrt(3t)):Let's use the chain rule to differentiate this function.
Differentiate the outer function: d/dt(tan(sqrt(3t)))Differentiate the inner function: d/dt(sqrt(3t)) = (1/2)(3t)^(-1/2)(3)Apply the chain rule: d/dt(tan(sqrt(3t))) = (1/2)(3t)^(-1/2)(3)(sec^2(sqrt(3t)))Therefore, the differential of y = tan(sqrt(3t)) is dy/dt = (1/2)(3t)^(-1/2)(3)(sec^2(sqrt(3t))).
Differentiation of y = 4 - v^2/4 + v^2:Let's differentiate this function using the power rule and the sum/difference rule for derivatives.
Differentiate the constant term: d/dv(4) = 0Differentiate the first term: d/dv(-v^2/4) = (-1/4)(2v) = -v/2Differentiate the second term: d/dv(v^2) = 2vTherefore, the differential of y = 4 - v^2/4 + v^2 is dy/dv = 0 - v/2 + 2v = 3v/2.
Learn more:About differential here:
https://brainly.com/question/31391186
#SPJ11
what is the volume of a tissue box with 1 ft x 2 ft x 3 ft ?
Answers
Answer:
V = 6 ft^3
Step-by-step explanation:
V = length * width * height
V = 1* 2* 3
V = 6 ft^3
Answer:
6 ft³
Step-by-step explanation:
V = lwh
V = 1 × 2 × 3
V = 6 ft³
the length of a rectangular piece of sheet metal is longer than its width. a square piece that measures on each side is cut from each corner, then the sides are turned up to make a box with volume . find the length and width of the original piece of sheet metal.
Answers
The width of the original piece of sheet metal is (w^2 - l^2)/(3w + 3l), and the length is (l^2 - w^2)/(3w + 3l).
To solve this problem, we can use the formula for the volume of a rectangular box, which is V = lwh, where l is the length, w is the width, and h is the height.
First, let's find the height of the box. Since we cut squares from each corner, the height of the box is the length of the square that was cut out. Let's call this length x.
The width of the box is the original width minus the lengths of the two squares that were cut out, which is w - 2x.
Similarly, the length of the box is the original length minus the lengths of the two squares that were cut out, which is l - 2x.
Now we can write the volume of the box in terms of x, w, and l:
V = (w - 2x)(l - 2x)(x)
Expanding this expression, we get:
V = x(4wl - 4wx - 4lx + 8x^2)
Simplifying further:
V = 4x^3 - 4wx^2 - 4lx^2 + 4wlx
To find the dimensions of the original piece of sheet metal, we need to maximize this volume. We can do this by taking the derivative of the volume with respect to x and setting it equal to zero:
dV/dx = 12x^2 - 8wx - 8lx + 4wl = 0
Solving for x, we get:
x = (2wl)/(3w + 3l)
Now we can use this value of x to find the width and length of the original piece of sheet metal:
w - 2x = w - 2(2wl)/(3w + 3l) = (w^2 - l^2)/(3w + 3l)
l - 2x = l - 2(2wl)/(3w + 3l) = (l^2 - w^2)/(3w + 3l)
Know more about volume of a rectangle here:
https://brainly.com/question/21308574
#SPJ11
Create your own false statment but not from the one's given

Answers
A false statement could be that
"the maximum height attained by the diver was 20 feet
find a · b. |a| = 2, |b| = 7, the angle between a and b is 2/3
Answers
The product of vectors a and b is approximately 5.292.
To find the product of two vectors a and b, we need to use the dot product formula which is a · b = |a| |b| cosθ, where |a| and |b| are the magnitudes of vectors a and b, and θ is the angle between them.
In this case, we are given that |a| = 2 and |b| = 7, and the angle between a and b is 2/3. We can use this information to find cosθ as follows:
cosθ = cos(2/3) ≈ 0.378
Now, we can substitute the values into the formula:
a · b = |a| |b| cosθ
a · b = 2 * 7 * 0.378
a · b ≈ 5.292
Therefore, the product of vectors a and b is approximately 5.292.
Learn more about magnitudes here:
https://brainly.com/question/2596740
#SPJ11
An urn contains 3 red and 7 black balls. Players A and B alternate withdrawing balls from the urn consecutively until a red ball is selected. Find the probability that A selects the red ball.
Answers
The probability that A selects the red ball is 3/6 = 1/2.
Given that an urn contains 3 red and 7 black balls. Players A and B alternate withdrawing balls from the urn consecutively until a red ball is selected. We need to find the probability that A selects the red ball.Let us assume that A draws first and B draws next. The probability that A selects the red ball is given as follows:Probability of A selecting the red ball = (number of favorable outcomes) / (total number of outcomes)Number of favorable outcomes = 3Total number of outcomes = 3 + 7 = 10
The probability that A selects the red ball is given as:P(A selects the red ball) = (number of favorable outcomes) / (total number of outcomes)P(A selects the red ball) = 3/10Now, let B draw first and A draws next. In this case, A can select the red ball only if B fails to select the red ball. Hence, the probability that A selects the red ball is given as:P(A selects the red ball) = (probability that B does not select the red ball and A selects the red ball)P(A selects the red ball) = (7/10) * (3/6)P(A selects the red ball) = (7/10) * (1/2)P(A selects the red ball) = (7/20)Therefore, the probability that A selects the red ball is 3/10 when A draws first and 7/20 when B draws first. Since players A and B alternate withdrawing balls, the probability that A selects the red ball is the weighted average of these two probabilities.P(A selects the red ball) = (1/2) * (3/10) + (1/2) * (7/20)P(A selects the red ball) = (3/20) + (7/40)P(A selects the red ball) = (9 + 7) / 40P(A selects the red ball) = 16 / 40P(A selects the red ball) = 4 / 10P(A selects the red ball) = 2 / 5.That the probability that A selects the red ball is 2/5.
To know more about probability visit :-
https://brainly.com/question/31828911
#SPJ11
The circumference () C of a circle is 18 18 centimeters. Which formula can you use to find the radius () r if you know that =2π C = 2 π r ? CLEAR CHECK =2π r = C 2 π =2π r = 2 C π =π2 r = π C 2 =2π
Answers
The formula to find the radius (r) of a circle when you know the circumference (C) is r = C/(2π).
The formula presented derived from the formula for the circumference of a circle, which is C = 2πr. By rearranging the equation and isolating the radius (r) on one side, we get r = C/(2π).
So, if the circumference (C) of a circle is 18 centimeters, you can use the formula r = C/(2π) to find the radius (r). Plugging in the given value for the circumference (C), we get:
r = 18/(2π)
Simplifying the equation gives:
r = 9/π
Therefore, the radius (r) of the circle is 9/π centimeters.
In conclusion, the formula you can use to find the radius (r) of a circle when you know the circumference (C) is r = C/(2π).
See more about circumference at https://brainly.com/question/20489969.
#SPJ11
What is the solution set to the inequality?
-X + 3 > 5 or 4x > -8
X > -2 or x>-2
x < -2 orx > -0.5
x < -2 orx < -0.5
O x< -2 or x 2-2
Answers
Answer:
Step-by-step explanation:
-x+3 > 5 0r 4x > -8
-x > 2 or x > -8/4
x< -2 or x > -2
Pls help I’m stuck with this problem

Answers
Answer:
463×10³
463×1000
=0.463
What is the surface area of the rectangular prism below?

Answers
...........................
Answer:
D. 490
Step-by-step explanation:
If you multiply all you get 490 D
Please help immediately
Show your work

Answers
Answer:
a + 7
Step-by-step explanation:
x^2 + 2x - 8. on [5,a]
(f(a)-f(5))/( a - 5 )
(( a^2 + 2a - 8 ) - 27 ) / a - 5
( a^2 + 2a - 35 ) / a - 5
(a - 5)(a + 7) / a - 5
a + 7
An electronics store purchases
laptops for $425.00. They use a
markup rate of 60%. How much do they
sell the laptop to their customers?
A) $680.00
C) $255.00
B) $450.50
D) $595.00
Please help and no links. :)
Answers
Answer:
255.00
Step-by-step explanation:
425.00 x .60 = 255
N Given the data X₁ = 1, X2 = 4, X3 = 5, X4 = 8, X5 = 10, evaluate Z(X, +5). 1=2
Answers
Given the data X₁ = 1, X2 = 4, X3 = 5, X4 = 8, X5 = 10, evaluate Z(X, +5). 1=2Z(X, +5) refers to the standard score of the score X, if it is taken as the new mean of the distribution.
In other words, Z(X, +5) represents how many standard deviations X is from the new mean, which is 5. To evaluate Z(X, +5), we first need to calculate the mean and standard deviation of the data set:Mean = (1+4+5+8+10)/5 = 28/5 = 5.6Standard deviation.
To calculate the standard deviation, we use the formula: σ = √[Σ(X-μ)²/N]where Σ means "the sum of," X is the data point, μ is the mean, and N is the sample size. Plugging in the values: σ = √[(1-5.6)² + (4-5.6)² + (5-5.6)² + (8-5.6)² + (10-5.6)² / 5] = √[79.84/5] = √15.968 = 3.994 .
To know more about distribution visit:
https://brainly.com/question/27369938
#SPJ11
The following data represent the monthly phone use, in minutes customer enrolled in fraud prevention program for the past 20 months: The phone company decides to use the upper fence as the cutoff point for the number of minutes at which the customer should be contacted_ What is the cutoff point? 339 489 458 480 463 358 458 430 350 388 501 536 The cutoff point is minutes_ (Round to the nearest minute.
Answers
This indicates that the cutoff value for the amount of minutes before contacting the consumer is 674 minutes, rounded to the closest minute.
What is quartiles?Quartiles are three numbers that divide sorted data into four equal portions with an equal amount of observations each. A quantile is a sort of quantile. The first quartile is sometimes known as the lower quartile or Q1. Second quartile: Also known as the median or Q2. Third quartile: Also known as the higher quartile or Q3.
Here,
To find the upper fence, we need to calculate the following statistics:
Q1 (first quartile), Q2 (median), and Q3 (third quartile) of the data
Interquartile range (IQR), which is the difference between Q3 and Q1
Upper fence, which is Q3 + 1.5 * IQR
First, we need to order the data in ascending order:
339, 350, 358, 388, 430, 458, 458, 463, 480, 489, 501, 536
Next, we can find the quartiles:
Q1 = 388
Q2 = 458
Q3 = 501
IQR = Q3 - Q1 = 501 - 388 = 113
Finally, we can calculate the upper fence:
Upper fence = Q3 + 1.5 * IQR = 501 + 1.5 * 113 = 674
This means that the cutoff point for the number of minutes at which the customer should be contacted is 674 minutes, rounded to the nearest minute.
To know more about quartiles,
https://brainly.com/question/29089547
#SPJ4
problem 5 (30 points, each 10 points). in a chemical plant, 24 holding tanks are used for final product storage. four tanks are selected at random and without replacement. suppose that four of the tanks contain material in which the viscosity exceeds the customer requirements. 1. what is the probability that exactly one tank in the sample contains high-viscosity material? 2. what is the probability that at least one tank in the sample contains high-viscosity material? 3. in addition to the four tanks with high-viscosity levels, four different tanks contain material with high impurities. what is the probability that exactly one tank in the sample contains high-viscosity material and exactly one tank in the sample contains material with high impurities?
Answers
1. The probability of selecting exactly one tank with high-viscosity material is 0.
2. The probability of selecting at least one tank with high-viscosity material is 1.
3. The probability of selecting exactly one tank with high-viscosity material and exactly one tank with high impurities is 0.25.
1. The probability of selecting exactly one tank with high-viscosity material is calculated by the binomial distribution formula, P(X = n) = (nCx)p^x(1-p)^n-x, where n is the number of trials, x is the number of successes, and p is the probability of success. In this case, n = 4, x = 1, and p = 24/24 = 1. Therefore, P(X = 1) = (4C1)1^1(1-1)^4-1 = 0.
2. The probability of selecting at least one tank with high-viscosity material is calculated by the complement rule, P(X > 0) = 1 - P(X = 0). In this case, P(X > 0) = 1 - (4C0)1^0(1-1)^4-0 = 1.
3. The probability of selecting exactly one tank with high-viscosity material and exactly one tank with high impurities is calculated by the binomial distribution formula, P(X = n) = (nCx)p^x(1-p)^n-x, where n is the number of trials, x is the number of successes, and p is the probability of success. In this case, n = 8, x = 2, and p = 24/24 = 1. Therefore, P(X = 2) = (8C2)1^2(1-1)^8-2 = 0.25.
Learn more about probability here:
https://brainly.com/question/14206287
#SPJ4
Mark all the relative maximum points in the graph

Answers
\( \: \)
-7....-5....-3....-1....