Which of the following is equal to the expression listed below?35 + 28
Answers
Answer:
35+28=63
Step-by-step explanation:
first separate the numbers between the tens and ones like this
35 separated is 30 and 5
28 separated is 20 and 8
then you add the tens and ones like this:
30+20=50
and
5+8=13
lastly and the two sums together like this:
50+13=63
conclusion:
therefore with the steps above you can find that 35+28=63
also if your boring you can use a calculator :(
I don't care if I get brainliest I just wanted to help :).
bye :)
Related Questions
PLEASE ANSWER TOADAY !!!!!!!!!!!!!!!!!

Answers
Answer:
most likely next spring
Step-by-step explanation:
Step-by-step explanation:
answer that pls ty (ノ◕ヮ◕)ノ*:・゚✧
ありがとうと答えてください (ノ◕ヮ◕)ノ*:・゚✧

Answers
Answer:
1= 23
2= 0.5
3= 1.45
4= 0.07
Step-by-step explanation:
(hope this helps can i plz have brainlist :D hehe)
The area of a rectangle is 54 yd2, and the length of the rectangle is 3yd more than double the width. Find the dimensions of the rectangle.
Answers
Need Answer ASAP! 30 POINTS !
A recipe for a casserole calls for 1 cup of milk. If a chef currently has 0.5 gallons of milk, how many casseroles can the chef make?
Answers
Answer:
5
Step-by-step explanation:
0.3x
1
+0.1x
2
≤2.7→0.3x
1
+0.1x
2
≤1.8 Work through the simplex method step by step. How the solution changes (i.e., LP has optimal solutions or LP is unbounded or is infeasible)? Why?
Answers
The solution to the linear programming problem 0.3x₁ + 0.1x₂ ≤ 1.8 using the simplex method shows that the problem has optimal solutions.)
Convert the inequality into an equation by subtracting 1.8 from both sides:
0.3x₁ + 0.1x₂ - 1.8 ≤ 0
Introduce slack variables to convert the inequality into an equation:
0.3x₁ + 0.1x₂ + s₁ = 1.8
Set up the initial simplex tableau:
┌───┬───┬───┬───┬───┐
│ │ x₁ │ x₂ │ s₁ │ 1│
├───┼───┼───┼───┼───┤
│ 1│ 0.3│ 0.1│ 1 │1.8│
└───┴───┴───┴───┴───┘
```
Select the pivot column. Choose the column with the most negative coefficient in the bottom row. In this case, it is the second column (x₂).
Select the pivot row. Divide the numbers in the rightmost column (1.8) by the corresponding numbers in the pivot column (0.1) and choose the smallest positive ratio. In this case, the smallest positive ratio is 1.8/0.1 = 18. So the pivot row is the first row.
The simplex method is an iterative procedure that systematically improves the solution to a linear programming problem. It starts with an initial feasible solution and continues to find a better feasible solution until an optimal solution is obtained. In each iteration, the simplex method selects a pivot column and a pivot row to perform row operations, which transform the current tableau into a new tableau with improved objective function values. The process continues until the objective function values cannot be further improved or the linear programming problem is unbounded.
To know more about solution visit:
https://brainly.com/question/30109489
#SPJ11
The correct answer is
0.3x1+0.1x2≤2.7→0.3x1+0.1x2≤1.8 Work Through The Simplex Method Step By Step. How The Solution Changes (I.E., LP Has Optimal
LINEAR EQUATIONS HELP

Answers
Hey there! :)
Answer:
-1/3.
Step-by-step explanation:
Find the slope of the line using the slope formula:
\(m = \frac{\text{rise}}{\text{run}} = \frac{y_2 - y_1}{x_2 - x_1}\)
Use two points from the graph and plug them into the equation. We can use the points (0, 3) and (3, 2):
\(m = \frac{2 - 3}{3 - 0}\)
Simplify:
m = -1/3. This is the slope of the line.
Y=x/4-7;y=2 find the value of x for the given value of y
Answers
Answer:
do you mean y=x-4-7 cause I can't understand that
write a function drugpotency(loss, expire) that determines how many months a drug can remain in storage given a potency loss percentage (loss) and an expiration target (expire). for example, if a certain drug looses 4% of its effectiveness every month it is in storage, when its effectiveness is below 50% it is considered expired and must be discarded. the output from drugpotency(4.0, 50.0) would be:
Answers
Answer:
def drugPotency(loss,expire):
m=0
effectiveness=100
print('Month:',m,'\t','effectiveness:',effectiveness)
while effectiveness>=expire:
effectiveness=effectiveness*(1-loss/100)
m+=1
if effectiveness>=expire:
print('Month:',m,'\t','effectiveness:',effectiveness)
else:
print('Month:',m,'\t','effectiveness:',effectiveness,'DISCARDED')
drugPotency(4.0,50.0)
Step-by-step explanation:
Each table below lists the squared residuals for a line of fit for a certain set of data points. Find the sum of the squared residuals for each potential line of fit, and then determine which potential line is the true line of best fit.
c.) Square of Residual
.200
.116
.16
D) Square of Residual
.0036
.0016
.009

Answers
Answer:
c
Step-by-step explanation:
what is the chi-square value? round to the nearest hundredth.
Answers
Answer:
597
Step-by-step explanation: step by step explanation
Help pleaseeeeeeeeeeee
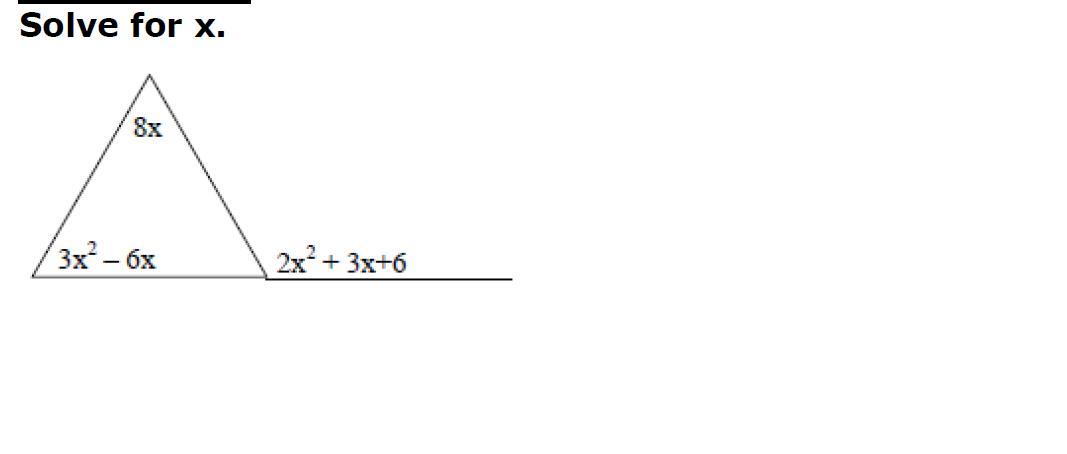
Answers
The sum of all the angles in a triangle is also 180°.
Let the missing angle be x°.
For the straight line:
x + 2x²+ 3x+ 6 = 180
x = 180 - (2x² + 3x + 6)
x = 180 - 2x² - 3x - 6
x = 174 - 2x² - 3x
For the missing angle in the triangle:
(174 - 2x² - 3x) + 8x + 3x² - 6x = 180
174 - 2x² - 3x + 8x + 3x² - 6x = 180
174 + x² - x = 180
x² - x + 174 - 180 = 0
x² - x - 6 = 0
(x + 2)(x - 3) = 0
x + 2 = 0 or x - 3 = 0
x = -2 or x = 3
The answer is x = -2 or x = 3
9514 1404 393
Answer:
x = 3
Step-by-step explanation:
An exterior angle is equal to the sum of the remote interior angles:
2x^2 +3x +6 = (8x) +(3x^2 -6x)
x^2 -x -6 = 0 . . . . . . subtract the left-side expression, put in standard form
(x -3)(x +2) = 0 . . . . .factor
The value of x is a value that makes a factor zero. These factors are zero when x=3 or x=-2. Only positive values of x will give positive angles in this geometry. The only useful solution is ...
x = 3
Find the surface area of a square pyramid with side length 2 m and slant height 3 m.
Answers
Answer: The surface area of a square pyramid with a side length of 2m and slant height of 3m is 12 square meters.
Step-by-step explanation:
The surface area of a square pyramid can be calculated using the formula:
Surface area = Base area + 4 * (Area of one of the lateral faces)
The base area of the pyramid is the area of the square base, which is the side length squared: 2m * 2m = 4m^2
To find the area of one of the lateral faces, we can use the Pythagorean theorem to find the length of the face, which is the hypotenuse of a right triangle with the slant height and half of the side length as the other two sides.
so, (1/2 * 2m)^2 + 3^2 = x^2
x= (1/2 * 2m)^2 + 3^2
x = 2
Therefore, the surface area of the pyramid is:
Surface area = 4m^2 + 4 * 2m^2 = 4m^2 + 8m^2 = 12m^2
So, the surface area of a square pyramid with a side length of 2m and a slant height of 3m is 12 square meters.
Use the given endpoint Rand midpoint M of RSto find the coordinates of the other endpoint.
R(5,2), M (6,4)
Answers
Answer:
Step-by-step explanation:
(x+5)/2 = 6
x + 5 = 12
x = 7
(y + 2)/2= 4
y + 2 = 8
y = 6
(7, 6)
You take out a loan for $7,500 and plan to pay it back over 4 years. Your credit score is 750. How much will you save by having a credit score that is higher than 700?

Answers
Answer:
Step-by-step explanation:
The difference between a credit score of 699 and 700 is 14.125% and 13.125% APR interest rate for a 4-year (48-months) loan of $7500.
With APR of 14.125% compounded yearly, the total loan payment after 4 years is
= $7500 * (1 + 14.125%)^4
= $7500 * 1.14125^4
= $12722.85
With APR of 13.125% compounded yearly, the total loan payment after 4 years is
= $7500 * (1 + 13.125)^4
= $7500 * 1.13125^4
= $12282.75
So you will save by having a credit score above 700:
= $12722.85 - $12282.75
= $440.10
Please note that posting the same question multiple times does not usually help in getting an answer :)
I need help ASAP The angle measures of a triangle are shown in the diagram. 50° les (3x - 10) ° What is the value of x? F25 G 20 H 10 ) 28 search C

Answers
Answer:
The answer is 28
Step-by-step explanation:
Since the total measurements of triangle corners are equal to 180
Then
\(2x + 3x - 10 + 50 = 180 \\ 5x - 40 = 180 \\ 5x = 140 \\ x = 28\)
which of the relations given by the following sets of ordered pairs is a function?
a. {(5,2),(4,2),(3,2),(2,2),(1,2)}{(5,2),(4,2),(3,2),(2,2),(1,2)}
b. {(−4,−2),(−1,−1),(3,2),(3,5),(7,10)}{(−4,−2),(−1,−1),(3,2),(3,5),(7,10)}
c. {(−8,−3),(−6,−5),(−4,−2),(−2,−7),(−1,−4)}{(−8,−3),(−6,−5),(−4,−2),(−2,−7),(−1,−4)}
d. {(−6,4),(−3,−1),(0,5),(1,−1),(2,3)}
Answers
{(5, 2), (4, 2), (3, 2), (2, 2), (1, 2)}, {(−8, −3), (−6, −5), (−4, −2), (−2, −7), (−1, −4)} and {(−6, 4), (−3, −1), (0, 5), (1, −1), (2, 3)} are the sets of ordered pairs considered as a function.
{(−4, −2), (−1, −1), (3, 2), (3, 5), (7, 10)} is not a function.
In mathematics, ordered pair is a pair of numbers that are written in a specific order. They are generally written in (x, y) form. For example (3, 5) is an ordered pair.
The function can also be represented by a set of ordered pairs. A function Is a set of ordered pairs in which no two different ordered pairs have the same value of x coordinate.
Option (a) : {(5, 2),(4, 2),(3, 2),(2, 2),(1, 2)}
No two ordered pairs have the same value of the x coordinate.
So it is a function.
Option (b) : {(-4, -2),(-1, -1),(3, 2),(3, 5),(7, 10)}
Two ordered pairs have the same value of x coordinate (3, 2) and (3, 5).
So, it can not be considered a function.
Option (c) : {(-8, -3),(-6, -5),(-4, -2),(-2, -7),(-1, -4)}
No two ordered pairs have the same value of the x coordinate.
So it is a function.
Option (d) : {(-6, 4),(-3, -1),(0, 5),(1, -1),(2, 3)}
No two ordered pairs have the same value of the x coordinate.
So it is a function.
Therefore, Options (a), (c), and (d) are the functions.
Option (b) is not a function.
For more questions on ordered pairs as function
https://brainly.com/question/11267211
#SPJ4
Find the total surface area of this cone.
Leave your answer in terms of T.
24.in
SA =? - in2

Answers
Answer:
SA = 360π in²
Step-by-step explanation:
The slant height l is the hypotenuse of the right triangle inside the cone.
Using Pythagoras' identity to find l
l² = 24² + 10² = 576 + 100 = 676 ( take the square root of both sides )
l = \(\sqrt{676}\) = 26
Then
SA = πrl + πr²
= (π × 10 × 26) + (π × 10²)
= 260π + 100π
= 360π in²
Unit 3 parallel and perpendicular lines Homework 2, please help quickly

Answers
Answer:
Step-by-step explanation:
Since, lines l and m are parallel and a transverse is intersecting these lines.
5). (9x + 2)° = 119° [Alternate intrior angles]
9x = 117 ⇒ x = 13
6). (12x - 8)° + 104° = 180°
12x = 180 - 96
x = \(\frac{84}{12}\) ⇒ x = 7
7). (5x + 7) = (8x - 71) [Alternate exterior angles]
8x - 5x = 71 + 7
3x = 78
x = 26
8). (4x - 7) = (7x - 61) [Corresponding angles]
7x - 4x = -7 + 61
3x = 54
x = 18
9). (9x + 25) = (13x - 19) [Corresponding angles]
13x - 9x = 25 + 19
4x = 44
x = 11
(13x - 19)° + (17y + 5)° = 180°[Linear pair of angles are supplementary]
(13×11) - 19 + 17y + 5 = 180
129 + 17y = 180
17y = 180 - 129
y = 3
10). (3x - 29) + (8y + 17) = 180 [linear pair of angles are supplementary]
3x + 8y = 180 + 12
3x + 8y = 192 -----(1)
(8y + 17) = (6x - 7) [Alternate exterior angles]
6x - 8y = 24
3x - 4y = 12 -----(2)
Equation (1) - equation (2)
(3x + 8y) - (3x - 4y) = 192 - 12
12y = 180
y = 15
From equation (1),
3x + 8(15) = 192
3x + 120 = 192
x = 24
11). (3x + 49)° = (7x - 23)° [Corresponding angles]
7x - 3x = 49 + 23
4x = 72 ⇒ x = 18
(11y - 1)° = (3x)° [Corresponding angles]
11y = 3×18 + 1
11y = 55 ⇒ y = 5
12). (5x - 38)° = (3x - 4)° [Corresponding angles]
5x - 3x = 38 - 4
2x = 34
x = 17
(7y - 20)° + (5x - 38)° + 90° = 180°
[Sum of interior angles of a triangle = 180°]
7y + 5x - 58 = 90
5x + 7y = 148
5×17 + 7y = 148
85 + 7y = 148
7y = 148 - 85
y = \(\frac{63}{7}=9\)
Angles can be congruent based n several theorems; some of these theorems are: corresponding angles, vertical angles, alternate exterior angles and several others.
The values of x and y are:
5. \(\mathbf{x = 13}\)6. \(\mathbf{x = 7}\)7. \(\mathbf{x= 26}\)8. \(\mathbf{x = 18}\)9. \(\mathbf{x = 11}\) and \(\mathbf{y = 7}\)10. \(\mathbf{x = 24}\) and \(\mathbf{y = 15}\)11. \(\mathbf{x = 18}\) and \(\mathbf{y =5}\)12. \(\mathbf{x = 17}\) and \(\mathbf{y=9}\)Question 5:
Angles (9x + 2) and 119 are alternate angles.
Alternate angles are equal. So, we have:
\(\mathbf{9x +2 = 119}\)
Subtract 2 from both sides
\(\mathbf{9x = 117}\)
Divide both sides by 9
\(\mathbf{x = 13}\)
Question 6:
Angles (12x - 8) and 104 are interior angles.
Interior angles add up to 180. So, we have:
\(\mathbf{12x -8 + 104 = 180}\)
Collect like terms
\(\mathbf{12x = 180 - 104 + 8}\)
\(\mathbf{12x = 84}\)
Divide both sides by 12
\(\mathbf{x = 7}\)
Question 7:
Angles (5x + 7) and (8x - 71) are alternate exterior angles.
Alternate exterior angles are equal. So, we have:
\(\mathbf{5x + 7 = 8x - 71}\)
Collect like terms
\(\mathbf{8x - 5x= 71 + 7}\)
\(\mathbf{3x= 78}\)
Divide both sides by 3
\(\mathbf{x= 26}\)
Question 8:
Angles (4x - 7) and (7x - 61) are corresponding angles.
Corresponding angles are equal. So, we have:
\(\mathbf{4x - 7 = 7x - 61}\)
Collect like terms
\(\mathbf{4x - 7x = 7 - 61}\)
\(\mathbf{- 3x = -54}\)
Divide both sides by -3
\(\mathbf{x = 18}\)
Question 9:
Angles (9x + 25) and (13x - 19) are corresponding angles.
Corresponding angles are equal. So, we have:
\(\mathbf{9x + 25 = 13x - 19}\)
Collect like terms
\(\mathbf{9x -13x = -25 - 19}\)
\(\mathbf{-4x = -44}\)
Divide both sides by -4
\(\mathbf{x = 11}\)
Angles (17y + 5) and (13x - 19) are supplementary angles.
So, we have:
\(\mathbf{17y + 5 = 13x - 19}\)
Substitute 11 for x
\(\mathbf{17y + 5 = 13\times 11 - 19}\)
\(\mathbf{17y + 5 = 124}\)
Subtract 5 from both sides
\(\mathbf{17y = 119}\)
Divide both sides by 17
\(\mathbf{y = 7}\)
Question 10:
Angles (3x - 29) and (6x - 7) add up to 180
So, we have:
\(\mathbf{3x -29 + 6x - 7 = 180}\)
Collect like terms
\(\mathbf{3x + 6x = 180 + 7 + 29}\)
\(\mathbf{9x = 216}\)
Divide both sides by 9
\(\mathbf{x = 24}\)
Angles (3x - 29) and (8y + 17) are supplementary angles.
So, we have:
\(\mathbf{3x - 29 + 8y + 17 = 180}\)
Substitute 24 for x
\(\mathbf{3 \times 24 - 29 + 8y + 17 = 180}\)
\(\mathbf{43 + 8y + 17 = 180}\)
Collect like terms
\(\mathbf{8y = 180 - 43 - 17}\)
\(\mathbf{8y = 120}\)
Divide both sides by 8
\(\mathbf{y = 15}\)
Question 11:
Angles (7x - 23) and (49 + 3x) are corresponding angles
So, we have:
\(\mathbf{7x - 23 = 49 + 3x}\)
Collect like terms
\(\mathbf{7x - 3x = 49 + 23}\)
\(\mathbf{4x = 72}\)
Divide both sides by 4
\(\mathbf{x = 18}\)
Angles 3x and (11y - 1) are corresponding angles.
So, we have:
\(\mathbf{3x = 11y - 1}\)
Substitute 18 for x
\(\mathbf{3 \times 18 = 11y - 1}\)
\(\mathbf{54 = 11y - 1}\)
Collect like terms
\(\mathbf{11y =54+ 1}\)
\(\mathbf{11y =55}\)
Divide both sides by 11
\(\mathbf{y =5}\)
Question 12:
Angles (5x - 38) and (3x - 4) are corresponding angles
So, we have:
\(\mathbf{5x - 38 = 3x - 4}\)
Collect like terms
\(\mathbf{5x - 3x = 38 - 4}\)
\(\mathbf{2x = 34}\)
Divide both sides by 2
\(\mathbf{x = 17}\)
Angles (7y - 20) and (5x - 38) are angles at the other legs of a right-angled triangle.
So, we have:
\(\mathbf{7y - 20 +5x - 38 = 90}\)
Substitute 17 for x
\(\mathbf{7y - 20 +5 \times 17 - 38 = 90}\)
\(\mathbf{7y+ 27 = 90}\)
Collect like terms
\(\mathbf{7y=- 27 +90}\)
\(\mathbf{7y=63}\)
Divide both sides by 7
\(\mathbf{y=9}\)
Read more about congruence angles at:
https://brainly.com/question/24623240
Determine which slope is the steepest. Explain why it is the steepest.
A) Slope=2
B) Slope= 1/2
C)Slope=-4
Answers
Answer:
Answer choice C
Step-by-step ex. 4 is the greatest number out of explanation:
The greater the absolute value is, the steeper it is. In this case, the absolute value of -4 is positive 4 since the absolute value shows how far a number is a ways from zero and is always positive. 4 is the largest number out of all of these choices which means it is the steepest slope.
A circle with an area of 10pi cm square? is dilated so that its image has an area of 25pi cm square?. What is the scale factor of the dilation? Round to two decimal places (hundreths).
Answers
The scale factor of the dilation is 4.472.
What is Scale Factor?A scale factor is a numerical value that can be used to alter the size of any geometric figure or object in relation to its original size. It is used to find the missing length, area, or volume of an enlarged or reduced figure as well as to draw the enlarged or reduced shape of any given figure. It should be remembered that the scale factor only affects how big a figure is, not how it looks.
Given:
Area of Circle = 10 π
This is dilated so that its image has an area of 25pi cm square.
For Original Circle
πr² = 10 π
r² = 10
r= √10
and, For dilated circle
πR² = 25 π
R² = 25
R = √25
R= 5
So, the scale factor is
R/ r = 5/ √10
R/r = 4.472
Learn more about scale Factor here:
https://brainly.com/question/30215119
#SPJ1
please help me on this question ASAP
i need it dont by midnight and its already 10:30.

Answers
Answer:
a) 3(17 )+ 4(9) = 81
b) 13.5m/s^2
Step-by-step explanation:
trust
given that z is a standard normal random variable, what is the value of z if the between -z and z is 0.901
Answers
The value of z that corresponds to a cumulative probability of 0.901 can be found by using the standard normal distribution table or a statistical calculator and that is approximately -1.67.
In the standard normal distribution, the area under the curve between -z and z represents the cumulative probability from negative infinity to z. Since the distribution is symmetric, the area from negative infinity to -z is also 0.5 - 0.901/2 = 0.0495.
To find the value of z, we need to locate the z-score that corresponds to an area of 0.0495 in the standard normal distribution. By looking up this value in the standard normal distribution table or using a statistical calculator, we find that z is approximately -1.67.
Therefore, the value of z that corresponds to a cumulative probability of 0.901 is approximately -1.67.
To learn more about statistical calculator click here : brainly.com/question/30765535
#SPJ11
Hello please solve this with steps
List the possible rational zeros of
f(x)= x^3-6x^2+6x-18 using the rational zero theorem

Answers
Answer:
±{1, 2, 3, 6, 9, 18}
Step-by-step explanation:
You want the possible rational zeros of f(x)= x^3-6x^2+6x-18.
Rational root theoremThe rational root theorem tells you the possible rational zeros are of the form ...
±{divisors of the constant term} / {divisors of the leading coefficient}
Here, the leading coefficient is 1, so its only divisor is 1.
The constant term is 18, and its divisors are 1, 2, 3, 6, 9, 18.
The possible rational roots are ±{1, 2, 3, 6, 9, 18}.
__
Additional comment
A graph shows the only real root is between 5 and 6, so none of the roots are rational.

Lu is graphing the ordered pair (3,5). Starting at the origin, what does she
need to do? *
A. Move 3 units up and 5 units to the right, and draw a dot at that point.
B. Move 3 units up and 3 units to the right, and draw a dot at that point.
O
C. Move 3 units to the right and 5 units up, and draw a dot at that point.
D. Move 5 units to the right and 3 units up, and draw a dot at that point.
Answers
Answer:
C. Move 3 units to the right and 5 units up, and draw a dot at that point.
Step-by-step explanation:
My YT is YoungGodlyFN is this helped!
(b) does this sample provide a significant evidence, at a 10% level of significance, that the average salary of all entry-level computer engineers is different from 80,000? explain.
Answers
Based on the given information, it seems that you want to determine if the average salary of all entry-level computer engineers is significantly different from $80,000 at a 10% level of significance.
To do this, you can perform a hypothesis test using these steps:
1. State the null hypothesis (H0): The average salary is equal to $80,000.
2. State the alternative hypothesis (H1): The average salary is different from $80,000.
3. Choose a 10% level of significance (α = 0.10).
4. Calculate the test statistic and corresponding p-value using the sample data.
5. Compare the p-value to the level of significance (α).
6. Draw a conclusion:
- If the p-value is less than or equal to α (0.10), you reject the null hypothesis (H0) and conclude that there is significant evidence that the average salary of all entry-level computer engineers is different from $80,000.
- If the p-value is greater than α (0.10), you fail to reject the null hypothesis (H0) and cannot conclude that the average salary is significantly different from $80,000.
To learn more about null hypothesis : brainly.com/question/28920252
#SPJ11
Someone pls help me I will make you brain

Answers
Answer:
the answer is X= -1
the line is touching coordinates (-1,0)
product of x 3(x 2 + 5x + 1)
Answers
..............
hope this helps :)

~hey~The price for the car was reduced five thousand, six hundred seventy-two dollars. The
final price for the car was nine thousand, five hundred thirty-five dollars. What was the
original price? $
Answers
Answer:
Your answer is 15,207
Step-by-step explanation:
9535 + 5672 = 15,207
Two circles are shown in the diagram.
Circles C 1 and C 2 are shown. The diameter of circle 1 is 1. The diameter of circle 2 is 2 r.
Since all circles are similar, a proportion can be set up using the circumference and diameter of each circle. Substitute the values d1 = 1, C1 = π, and d2 = 2r into the proportion.
StartFraction C 1 Over d 1 EndFraction = StartFraction C 2 Over d 2 EndFraction
Which shows how to correctly solve for C2, the circumference of any circle with radius r?
Because StartFraction pi Over 1 EndFraction = StartFraction C 2 Over 2 r EndFraction , C 2 = 2 r pi
Because StartFraction 1 Over pi EndFraction = StartFraction C 2 Over 2 r EndFraction , C 2 = StartFraction 2 r Over pi EndFraction
Because StartFraction pi Over 2 r EndFraction = StartFraction C 2 Over 1 EndFraction , C 2 = StartFraction pi Over 2 r EndFraction
Because StartFraction pi Over 1 EndFraction = StartFraction C 2 Over 4 r EndFraction , C 2 = 4 r pi
Answers
The correct equation is (a) because π/1 = C2/r2, \(C_2= 2\pi r\)
How to determine the correct equation?The complete question is added as an attachment
The given parameters are:
d1 = 1
d2 = 2r
The circumferences of the circles are calculated as:
C = πd
This gives
C1 = π * 1 = π
C2 = π * 2r = 2πr
So, we have:
C1 = π
C2 = 2πr
and
d1 = 1
d2 = 2r
Divide both equations
\(\frac{C_2}{d_1} = \frac{C_2}{d_2}\)
\(\frac{\pi}{1} = \frac{2\pi r}{2r}\)
This gives
\(\frac{\pi}{1} = \frac{C_2}{2r}\)
Hence, the correct equation is (a) because π/1 = C2/r2, \(C_2= 2\pi r\)
Read more about circumference at:
https://brainly.com/question/4268218
#SPJ1


Answer:
Its A
Step-by-step explanation:
Points Q, R, S, and T are shown on the number line. What is the distance between point Q and point S on the number line?
A) 2 units
B) 4 units
C) 6 units
D) 7 units

Answers
Point Q is at -4, so to get to Point S, which is at 2, you have to jump 6 units to get from Q to S.